平行四边形的性质教学设计
图片预览

文档简介
平行四边形的性质教学设计
【教学目标】
知识技能:
1.能准确叙述平行四边形的概念和其性质. 并能用符号语言表示.
2.能初步应用平行四边形的概念及其性质进行计算和证明
能力目标:
经历平行四边形的概念及其性质探究过程,发展合情推理能力,体会转化、数形结合等数学思想.
情感态度:
1.通过图片欣赏,感受数学在生活中的运用,激发学习热情.
2.在探究活动中,学会与他人合作、交流思维过程和探究结果.
【教学重点、难点】
重点:平行四边形的概念和性质
难点:平行四边形性质的探究和应用
【教学过程】
一、创设情景
1、图片欣赏-----生活中的四边形
2、这些图片中有你熟悉的图形吗?它们有什么共同特征?
3、怎样的四边形才是平行四边形
设计意图:通过图片欣赏,让学生感受平行四边形的不稳定性在生活中的应用,激发学生学习热情。并为导入平行四边形创设了情景。
二、问题探究
1、相关概念
·定义:两组对边分别平行的四边形是平行四边形
平行四边形几何语言表述:
定义:∵ AB∥CD, BC∥AD
∴四边形ABCD是平行四边形
·平行四边形相对的边称为对边,如AB与CD
相对的角称为对角,如∠A与∠C
设计意图 :让学生深刻理解平行四边形的含义,明确平行四边形与一般四边形的关系,用几何语言来表示平行四边形的定义不但能加深理解,而且为定义的运用、规范学生证明步骤打下基础。
2、你能用两个完全相同的三角形拼成一个平行四边形吗?如果可以,能有几种拼法?请试一试。
思考:根据刚才的拼摆过程的启示,你能发现拼出的平行四边形的对边之间、对角之间、邻角之间、对角线之间分别有什么关系?由此你能得到什么结论?
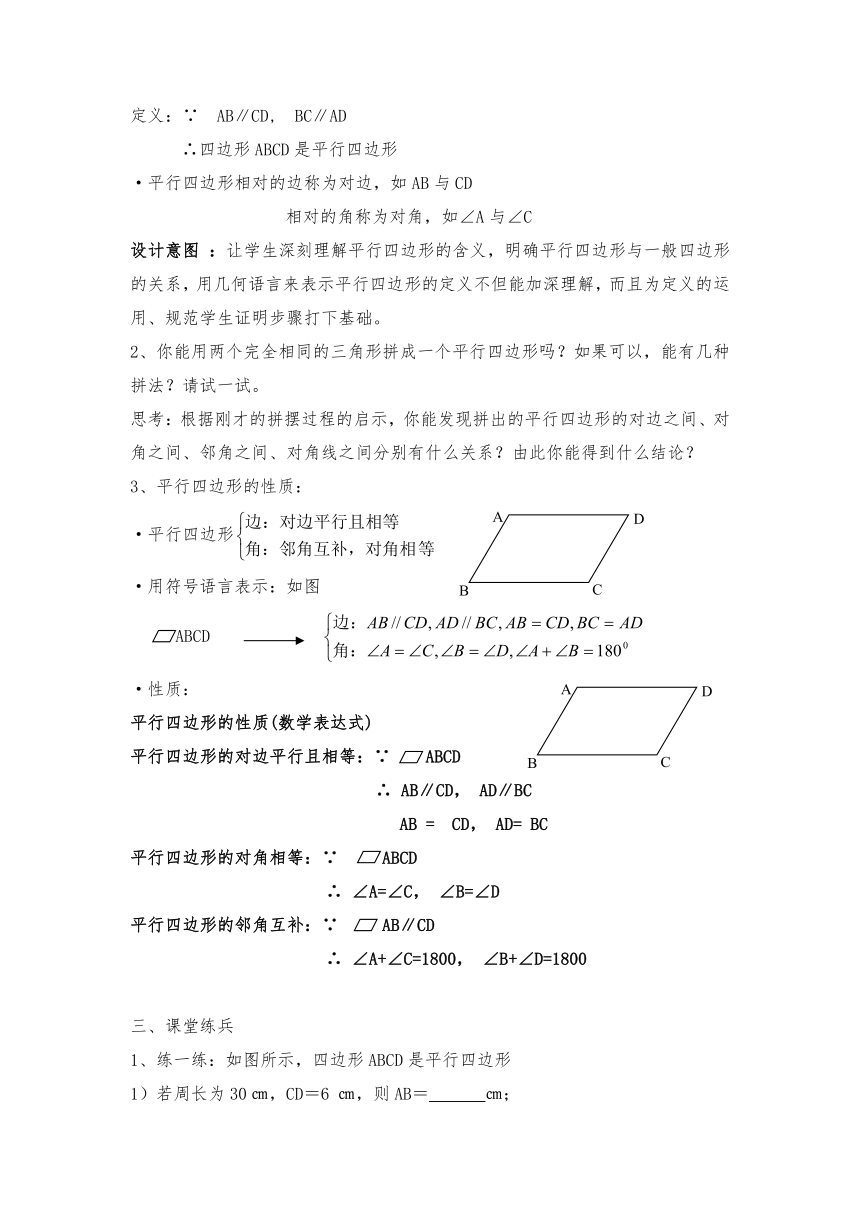
3、平行四边形的性质:
·平行四边形
·用符号语言表示:如图
ABCD
·性质:
平行四边形的性质(数学表达式)
平行四边形的对边平行且相等:∵ ABCD
∴ AB∥CD, AD∥BC
AB = CD, AD= BC
平行四边形的对角相等:∵ ABCD
∴ ∠A=∠C, ∠B=∠D
平行四边形的邻角互补:∵ AB∥CD
∴ ∠A+∠C=1800, ∠B+∠D=1800
三、课堂练兵
1、练一练:如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝;
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= 。∠C= ; ∠D= 。
3)若∠A+∠C=80°,则∠A= ;∠D= 。
4)若平行四边形ABCD的周长是40cm,且AB比BC长4cm,则CD= ,AD= 。
2、学以致用:
如图小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三边各长多少?
3、巩固提高:
1)在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
2)如图, ABCD中,AF⊥CD于F,AE⊥BC于E,∠D=60°求(1)∠EAF的度数。
设计意图:设计“练一练”是为了检查和巩固对平行四边形性质的理解;学以致用和巩固提高是进一步提升定理,利用定理进行计算、证明。并使学生明确解决有关平行四边形问题,有时转化为三角形来解决。
四、课堂检测
1.一个平行四边形的一个外角是38 °,这个平行四边形的每个内角的度数分别是多少?为什么?
2. 平行四边形ABCD 中, AB=5,BC=3,求它的周长.
五、感悟收获
1、经过本节课的学习,你有哪些收获?请和我们一起分享.
2、课堂小结
1)、平行四边形的定义:两组对边分别平行的四边形。
2)、平行四边形的性质。
平行四边形的对边相等且相等
平行四边形的对角相等
平行四边形的邻角互补
3)作业:必做题:P88练习第1、2题,P89习题16.1第1题。
两组对边分别平行
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
A
C
D
E
F
【教学目标】
知识技能:
1.能准确叙述平行四边形的概念和其性质. 并能用符号语言表示.
2.能初步应用平行四边形的概念及其性质进行计算和证明
能力目标:
经历平行四边形的概念及其性质探究过程,发展合情推理能力,体会转化、数形结合等数学思想.
情感态度:
1.通过图片欣赏,感受数学在生活中的运用,激发学习热情.
2.在探究活动中,学会与他人合作、交流思维过程和探究结果.
【教学重点、难点】
重点:平行四边形的概念和性质
难点:平行四边形性质的探究和应用
【教学过程】
一、创设情景
1、图片欣赏-----生活中的四边形
2、这些图片中有你熟悉的图形吗?它们有什么共同特征?
3、怎样的四边形才是平行四边形
设计意图:通过图片欣赏,让学生感受平行四边形的不稳定性在生活中的应用,激发学生学习热情。并为导入平行四边形创设了情景。
二、问题探究
1、相关概念
·定义:两组对边分别平行的四边形是平行四边形
平行四边形几何语言表述:
定义:∵ AB∥CD, BC∥AD
∴四边形ABCD是平行四边形
·平行四边形相对的边称为对边,如AB与CD
相对的角称为对角,如∠A与∠C
设计意图 :让学生深刻理解平行四边形的含义,明确平行四边形与一般四边形的关系,用几何语言来表示平行四边形的定义不但能加深理解,而且为定义的运用、规范学生证明步骤打下基础。
2、你能用两个完全相同的三角形拼成一个平行四边形吗?如果可以,能有几种拼法?请试一试。
思考:根据刚才的拼摆过程的启示,你能发现拼出的平行四边形的对边之间、对角之间、邻角之间、对角线之间分别有什么关系?由此你能得到什么结论?
3、平行四边形的性质:
·平行四边形
·用符号语言表示:如图
ABCD
·性质:
平行四边形的性质(数学表达式)
平行四边形的对边平行且相等:∵ ABCD
∴ AB∥CD, AD∥BC
AB = CD, AD= BC
平行四边形的对角相等:∵ ABCD
∴ ∠A=∠C, ∠B=∠D
平行四边形的邻角互补:∵ AB∥CD
∴ ∠A+∠C=1800, ∠B+∠D=1800
三、课堂练兵
1、练一练:如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝;
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= 。∠C= ; ∠D= 。
3)若∠A+∠C=80°,则∠A= ;∠D= 。
4)若平行四边形ABCD的周长是40cm,且AB比BC长4cm,则CD= ,AD= 。
2、学以致用:
如图小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三边各长多少?
3、巩固提高:
1)在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
2)如图, ABCD中,AF⊥CD于F,AE⊥BC于E,∠D=60°求(1)∠EAF的度数。
设计意图:设计“练一练”是为了检查和巩固对平行四边形性质的理解;学以致用和巩固提高是进一步提升定理,利用定理进行计算、证明。并使学生明确解决有关平行四边形问题,有时转化为三角形来解决。
四、课堂检测
1.一个平行四边形的一个外角是38 °,这个平行四边形的每个内角的度数分别是多少?为什么?
2. 平行四边形ABCD 中, AB=5,BC=3,求它的周长.
五、感悟收获
1、经过本节课的学习,你有哪些收获?请和我们一起分享.
2、课堂小结
1)、平行四边形的定义:两组对边分别平行的四边形。
2)、平行四边形的性质。
平行四边形的对边相等且相等
平行四边形的对角相等
平行四边形的邻角互补
3)作业:必做题:P88练习第1、2题,P89习题16.1第1题。
两组对边分别平行
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
A
C
D
E
F
