甘肃省天水成功高考学校2011-2012学年高三10月月考数学(文)试题
文档属性
| 名称 | 甘肃省天水成功高考学校2011-2012学年高三10月月考数学(文)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-18 00:00:00 | ||
图片预览





文档简介
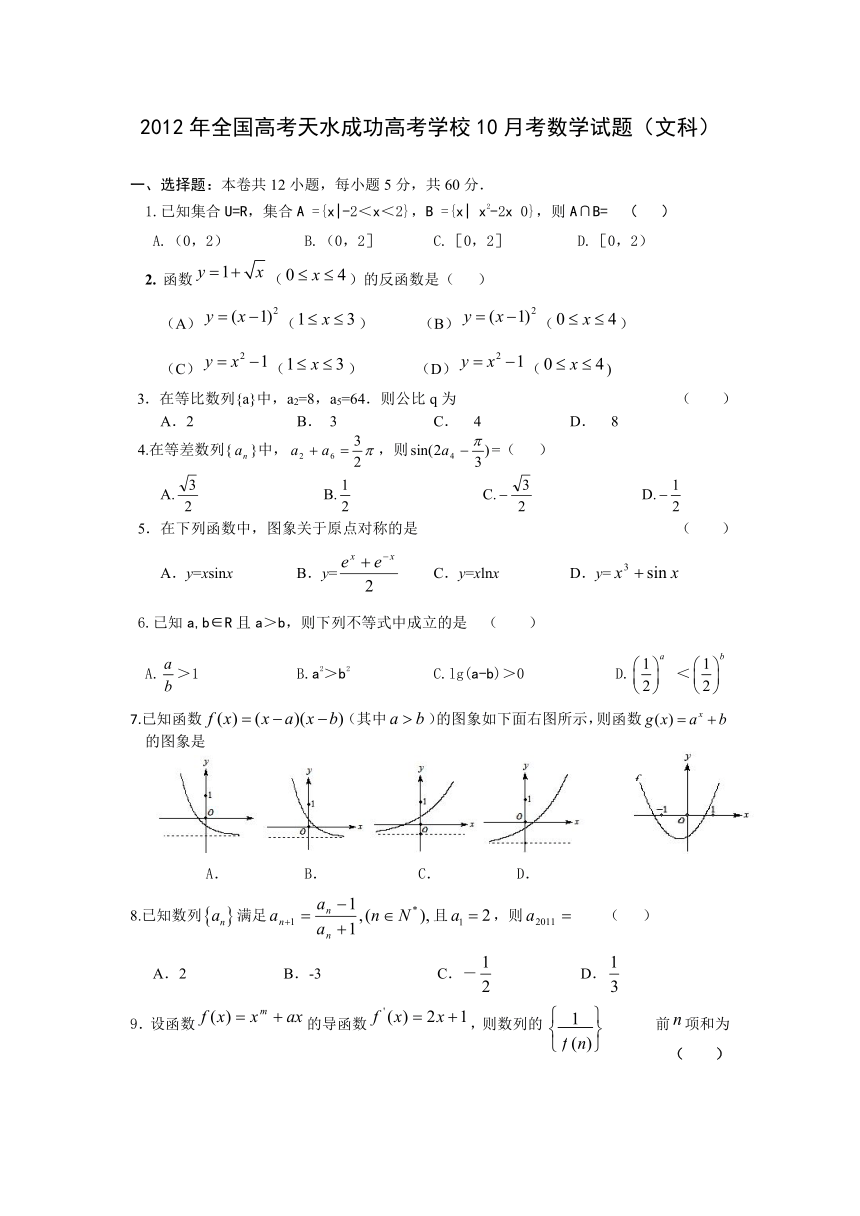
2012年全国高考天水成功高考学校10月考数学试题(文科)
一、选择题:本卷共12小题,每小题5分,共60分.
1.已知集合U=R,集合A ={x|-2<x<2},B ={x| x2-2x 0},则A∩B= ( )
A.(0,2) B.(0,2] C.[0,2] D.[0,2)
2. 函数()的反函数是( )
(A)( ( http: / / www. / )) (B)()
(C)( ( http: / / www. / )) (D)()
3.在等比数列{a}中,a2=8,a5=64.则公比q为 ( )
A.2 B. 3 C. 4 D. 8
4.在等差数列{}中,,则=( )
A. B. C. D.
5.在下列函数中,图象关于原点对称的是 ( )
A.y=xsinx B.y= C.y=xlnx D.y=
6.已知a,b∈R且a>b,则下列不等式中成立的是 ( )
A.>1 B.a2>b2 C.lg(a-b)>0 D. <
7.已知函数(其中 ( http: / / www. / ))的图象如下面右图所示,则函数的图象是
A. B. C. D.
8.已知数列满足且,则 ( )
A.2 B.-3 C.- D.
9.设函数的导函数,则数列的前项和为 ( )
A. B. C. D.
10.在等比数列中,是方程的两根,则的值为( )
A.11 B.-11 C. D.
11.已知函数所过定点的横、纵坐标分别是等差数列{}的第二项与第三项,若,数列的前项和为,则= ( )
A. B. C. D.
12.定义在上的函数满足且时,则 ( )
(A) (B) (C) (D)
二、填空题:本大题共4小题,每小题5分,共20分。
13.已知,则的值等于_____。
14.设,若是的等比中项,则的最小值为 。
15.已知数列的前项和满足,则数列的通项公式an=__________.
16.已知数列,其中,且数列为等比数列.则常数p=______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知y=是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求的解析式;
(2)求函数的单调递减区间及值域..
18.已知等差数列{an}的前n项和为Sn,且a3=5,S15=225。
(1)求数列{a n}的通项an;
(2)设bn=+2n,求数列{bn}的前n项和Tn。
19. 设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1=1, a3+b5=21, a5+b3=13.
(1)求{an}, {bn}的通项公式;(2)求数列{}的前n项和Sn;
20. 在数列.
(1)求证:数列是等差数列,并求数列的通项公式;
(2)设,数列项和为,求证:
21.已知,数列{an}为首项是1,以f(1)公比的等比数列;
数列{bn}中
(1)求数列{an}和{bn}的通项公式;
(2),{cn}的前n项和为Tn,证明:<4
22.已知函数
(1)若在的图象上横坐标为的点处存在垂直于y 轴的切线,求a 的值;
(2)若在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数的图象与函数的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
答题纸
一、选择题(本大题共12小题,每小题5分,满分60分..)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4个小题,每小题5分,共20分)
13. ___ 14. 15. ___ 16.
三、解答题:本大题共6小题,满分70分.解答须写出文字说明,证明过程和演算步骤.
17.解
18. 解
19. 解
20.解
21.解
22.解
答案
一、选择题:本卷共12小题,每小题5分,共60分.
1.已知集合U=R,集合A ={x|-2<x<2},B ={x| x2-2x 0},则A∩B=D
A.(0,2) B.(0,2] C.[0,2] D.[0,2)
2. 函数 ( http: / / www. / )()的反函数是( )
(A)() (B) ( http: / / www. / )()
(C)() (D) ( http: / / www. / )()
答案:A
3.在等比数列{a}中,a2=8,a5=64.则公比q为 ( )A
A.2 B. 3 C. 4 D. 8
4.在等差数列{}中,,则=( )D
A. B. C. D.
5.在下列函数中,图象关于原点对称的是 ( )D
A.y=xsinx B.y= C.y=xlnx D.y=
6.已知a,b∈R且a>b,则下列不等式中成立的是D
A.>1 B.a2>b2 C.lg(a-b)>0 D. <
7.已知函数(其中)的图象如下面右图所示,则函数 ( http: / / www. / )的图象是
A. B. C. D.
答案:A
8.已知数列满足且,则 ( )C
A.2 B.-3 C.- D.
9.设函数的导函数,则数列的前项和为 ( )A
A. B. C. D.
10.在等比数列中,是方程的两根,则的值为( )B
A.11 B.-11 C. D.
11.已知函数所过定点的横、纵坐标分别是等差数列{}的第二项与第三项,若,数列的前项和为,则= ( ) B
A. B. C. D.
12.定义在上的函数满足且时,则C
(A) (B) (C) (D)
第II卷 非选择题
二、填空题:本大题共4小题,每小题5分,共20分。
13.已知,则的值等于_____。
14.设,若是的等比中项,则的最小值为 。4
15.已知数列的前项和满足,则数列的通项公式an=__________.
解:
当时,
当时,
的通项公式为
说明:此题易忽略的情况。应满足条件。
16.已知数列,其中,且数列为等比数列.则常数p=______.
答案:p=2或p=3(提示可令n=1,2,3根据等比中项的性质建立关于p的方程,再说明p值对任意自然数n都成立
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知y=是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求的解析式;
(2)求函数的单调递减区间及值域..
解:(1)设
f(0)=8得c=8 2分
f(x+1)-f(x)=-2x+1得 a=-1,b=2
………………………………..5分
(2)=
当时, 8分
单调递减区间为(1 ,4) .值域…………………………..12分
18.已知等差数列{an}的前n项和为Sn,且a3=5,S15=225。
(1)求数列{a n}的通项an;
(2)设bn=+2n,求数列{bn}的前n项和Tn。
解:(1)设等差数列{a n}首项为a1,公差为d,由题意,得 ,解得 ,∴an=2n-1 ;
(2),
∴ =
19. 设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1=1, a3+b5=21, a5+b3=13.
(1)求{an}, {bn}的通项公式;(2)求数列{}的前n项和Sn;
19.解:(1)设{an}的公差为d,{bn}的公比为q,则依题意有q>0,……3分
解得d=2,q=2. 所以an=2n-1, bn=2n-1
((2), Sn=1+
2Sn=2+3+
两式相减得:
Sn=2+2(=2+
20. 在数列.
(1)求证:数列是等差数列,并求数列的通项公式;
(2)设,数列项和为,求证:
答案 . 解:(1)证明:
数列是等差数列
由
(2)
21.已知,数列{an}为首项是1,以f(1)公比的等比数列;
数列{bn}中
(1)求数列{an}和{bn}的通项公式;
(2),{cn}的前n项和为Tn,证明:<4
解:(1)
(2)
……10分
22.已知函数
(1)若在的图象上横坐标为的点处存在垂直于y 轴的切线,求a 的值;
(2)若在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数的图象与函数的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
答案 解:(1)依题意,
…………………………3分
(2)若在区间(—2,3)内有两个不同的极值点,
则方程在区间(—2,3)内有两个不同的实根,
但a=0时,无极值点,
∴a的取值范围为
(3)在(1)的条件下,a=1,要使函数的图象恰有三个交点,等价于方程,
即方程恰有三个不同的实根。
=0是一个根,
应使方程有两个非零的不等实根,
由 存在的图象恰有三个交点
f (x)
)
(
1
n
f
学号 班级 姓名
…………………………………………密…………………………………………封………………………………………线…………………………………
f (x)
)
(
1
n
f
2
3
2
1
2
2
3
2
n
n
n
n
一、选择题:本卷共12小题,每小题5分,共60分.
1.已知集合U=R,集合A ={x|-2<x<2},B ={x| x2-2x 0},则A∩B= ( )
A.(0,2) B.(0,2] C.[0,2] D.[0,2)
2. 函数()的反函数是( )
(A)( ( http: / / www. / )) (B)()
(C)( ( http: / / www. / )) (D)()
3.在等比数列{a}中,a2=8,a5=64.则公比q为 ( )
A.2 B. 3 C. 4 D. 8
4.在等差数列{}中,,则=( )
A. B. C. D.
5.在下列函数中,图象关于原点对称的是 ( )
A.y=xsinx B.y= C.y=xlnx D.y=
6.已知a,b∈R且a>b,则下列不等式中成立的是 ( )
A.>1 B.a2>b2 C.lg(a-b)>0 D. <
7.已知函数(其中 ( http: / / www. / ))的图象如下面右图所示,则函数的图象是
A. B. C. D.
8.已知数列满足且,则 ( )
A.2 B.-3 C.- D.
9.设函数的导函数,则数列的前项和为 ( )
A. B. C. D.
10.在等比数列中,是方程的两根,则的值为( )
A.11 B.-11 C. D.
11.已知函数所过定点的横、纵坐标分别是等差数列{}的第二项与第三项,若,数列的前项和为,则= ( )
A. B. C. D.
12.定义在上的函数满足且时,则 ( )
(A) (B) (C) (D)
二、填空题:本大题共4小题,每小题5分,共20分。
13.已知,则的值等于_____。
14.设,若是的等比中项,则的最小值为 。
15.已知数列的前项和满足,则数列的通项公式an=__________.
16.已知数列,其中,且数列为等比数列.则常数p=______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知y=是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求的解析式;
(2)求函数的单调递减区间及值域..
18.已知等差数列{an}的前n项和为Sn,且a3=5,S15=225。
(1)求数列{a n}的通项an;
(2)设bn=+2n,求数列{bn}的前n项和Tn。
19. 设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1=1, a3+b5=21, a5+b3=13.
(1)求{an}, {bn}的通项公式;(2)求数列{}的前n项和Sn;
20. 在数列.
(1)求证:数列是等差数列,并求数列的通项公式;
(2)设,数列项和为,求证:
21.已知,数列{an}为首项是1,以f(1)公比的等比数列;
数列{bn}中
(1)求数列{an}和{bn}的通项公式;
(2),{cn}的前n项和为Tn,证明:<4
22.已知函数
(1)若在的图象上横坐标为的点处存在垂直于y 轴的切线,求a 的值;
(2)若在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数的图象与函数的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
答题纸
一、选择题(本大题共12小题,每小题5分,满分60分..)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4个小题,每小题5分,共20分)
13. ___ 14. 15. ___ 16.
三、解答题:本大题共6小题,满分70分.解答须写出文字说明,证明过程和演算步骤.
17.解
18. 解
19. 解
20.解
21.解
22.解
答案
一、选择题:本卷共12小题,每小题5分,共60分.
1.已知集合U=R,集合A ={x|-2<x<2},B ={x| x2-2x 0},则A∩B=D
A.(0,2) B.(0,2] C.[0,2] D.[0,2)
2. 函数 ( http: / / www. / )()的反函数是( )
(A)() (B) ( http: / / www. / )()
(C)() (D) ( http: / / www. / )()
答案:A
3.在等比数列{a}中,a2=8,a5=64.则公比q为 ( )A
A.2 B. 3 C. 4 D. 8
4.在等差数列{}中,,则=( )D
A. B. C. D.
5.在下列函数中,图象关于原点对称的是 ( )D
A.y=xsinx B.y= C.y=xlnx D.y=
6.已知a,b∈R且a>b,则下列不等式中成立的是D
A.>1 B.a2>b2 C.lg(a-b)>0 D. <
7.已知函数(其中)的图象如下面右图所示,则函数 ( http: / / www. / )的图象是
A. B. C. D.
答案:A
8.已知数列满足且,则 ( )C
A.2 B.-3 C.- D.
9.设函数的导函数,则数列的前项和为 ( )A
A. B. C. D.
10.在等比数列中,是方程的两根,则的值为( )B
A.11 B.-11 C. D.
11.已知函数所过定点的横、纵坐标分别是等差数列{}的第二项与第三项,若,数列的前项和为,则= ( ) B
A. B. C. D.
12.定义在上的函数满足且时,则C
(A) (B) (C) (D)
第II卷 非选择题
二、填空题:本大题共4小题,每小题5分,共20分。
13.已知,则的值等于_____。
14.设,若是的等比中项,则的最小值为 。4
15.已知数列的前项和满足,则数列的通项公式an=__________.
解:
当时,
当时,
的通项公式为
说明:此题易忽略的情况。应满足条件。
16.已知数列,其中,且数列为等比数列.则常数p=______.
答案:p=2或p=3(提示可令n=1,2,3根据等比中项的性质建立关于p的方程,再说明p值对任意自然数n都成立
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知y=是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求的解析式;
(2)求函数的单调递减区间及值域..
解:(1)设
f(0)=8得c=8 2分
f(x+1)-f(x)=-2x+1得 a=-1,b=2
………………………………..5分
(2)=
当时, 8分
单调递减区间为(1 ,4) .值域…………………………..12分
18.已知等差数列{an}的前n项和为Sn,且a3=5,S15=225。
(1)求数列{a n}的通项an;
(2)设bn=+2n,求数列{bn}的前n项和Tn。
解:(1)设等差数列{a n}首项为a1,公差为d,由题意,得 ,解得 ,∴an=2n-1 ;
(2),
∴ =
19. 设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1=1, a3+b5=21, a5+b3=13.
(1)求{an}, {bn}的通项公式;(2)求数列{}的前n项和Sn;
19.解:(1)设{an}的公差为d,{bn}的公比为q,则依题意有q>0,……3分
解得d=2,q=2. 所以an=2n-1, bn=2n-1
((2), Sn=1+
2Sn=2+3+
两式相减得:
Sn=2+2(=2+
20. 在数列.
(1)求证:数列是等差数列,并求数列的通项公式;
(2)设,数列项和为,求证:
答案 . 解:(1)证明:
数列是等差数列
由
(2)
21.已知,数列{an}为首项是1,以f(1)公比的等比数列;
数列{bn}中
(1)求数列{an}和{bn}的通项公式;
(2),{cn}的前n项和为Tn,证明:<4
解:(1)
(2)
……10分
22.已知函数
(1)若在的图象上横坐标为的点处存在垂直于y 轴的切线,求a 的值;
(2)若在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数的图象与函数的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
答案 解:(1)依题意,
…………………………3分
(2)若在区间(—2,3)内有两个不同的极值点,
则方程在区间(—2,3)内有两个不同的实根,
但a=0时,无极值点,
∴a的取值范围为
(3)在(1)的条件下,a=1,要使函数的图象恰有三个交点,等价于方程,
即方程恰有三个不同的实根。
=0是一个根,
应使方程有两个非零的不等实根,
由 存在的图象恰有三个交点
f (x)
)
(
1
n
f
学号 班级 姓名
…………………………………………密…………………………………………封………………………………………线…………………………………
f (x)
)
(
1
n
f
2
3
2
1
2
2
3
2
n
n
n
n
同课章节目录
