河北省唐山市2013届高三9月摸底考试数学(理)试题
文档属性
| 名称 | 河北省唐山市2013届高三9月摸底考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-18 00:00:00 | ||
图片预览



文档简介
唐山市2012-2013学年度高三年级摸底考试
理科数学
第I卷
一、选择题(共60分)
(1)复数的虚部为
(A)2i (B)-2i (C)2 (D)-2
(2)设集合U=AUB, A={1,2,3}, AB={1},则=
(A){2} (B) {3} (C) {1,2,3} (D) {2,3}
(3)已知x,y满足,则z=2x-y的最大值为
lax-Y}-3,
(A) 2 (B)1 (C) -1 (D) 3
(4)已知双曲=1的离心串为2,则该双曲线的实轴长为
(A)2 (B)4 (C) 2 (D) 4
(5)若tnnθ=2,则cos2θ=
(A) (B)- (C) (D)-
(6)下列函数中,既是偶函数,又在区间(0. 3)内是增函数的是
(A) y= (B) y=coss
(C)y= (D) y=x+x-1
(7)在三棱锥P-ABC中,PA=PB=PC=,侧棱PA与底面ABC所成的角为60°,则该三棱锥外接球的体积为
(A)2 (B) (C)4 (D)
(8) 要得到函数的图象,只需将函数的图象
(A)向左平移个单位 (B)向右平移单位
(C)向左平移个单位 (D向右平移个单位
(9)空间几何体的三视图如图所示,则该几何体的表面积为
(A)6+2 (B)8+2
(C)8+2 (B)6+2
(10)一名小学生的年龄和身高(单位:cm)
的数据如下:
年龄x 6 7 8 9
身高y 118 126 136 144
由散点图可知,身高y与年龄x之间的线性回归直线方程为,预测该学生10岁时的身高为
(A) 154 .(B) 153 (C) 152 (D) 151
(11)己知△ABC的外心、重心、垂心分别为O,G,H,若,则=
(A)3 (B)2 (C) (D)
(12)已知函数f(x)满足f(x+1)[f(x)+1]=1。当x[0,1]时,f(x)=x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
(A)(0,) (B) (C) (D)
第II卷
二、城空题:本大题共4小颐,每小题5分,共20分。
(13)函数的定义域为_____
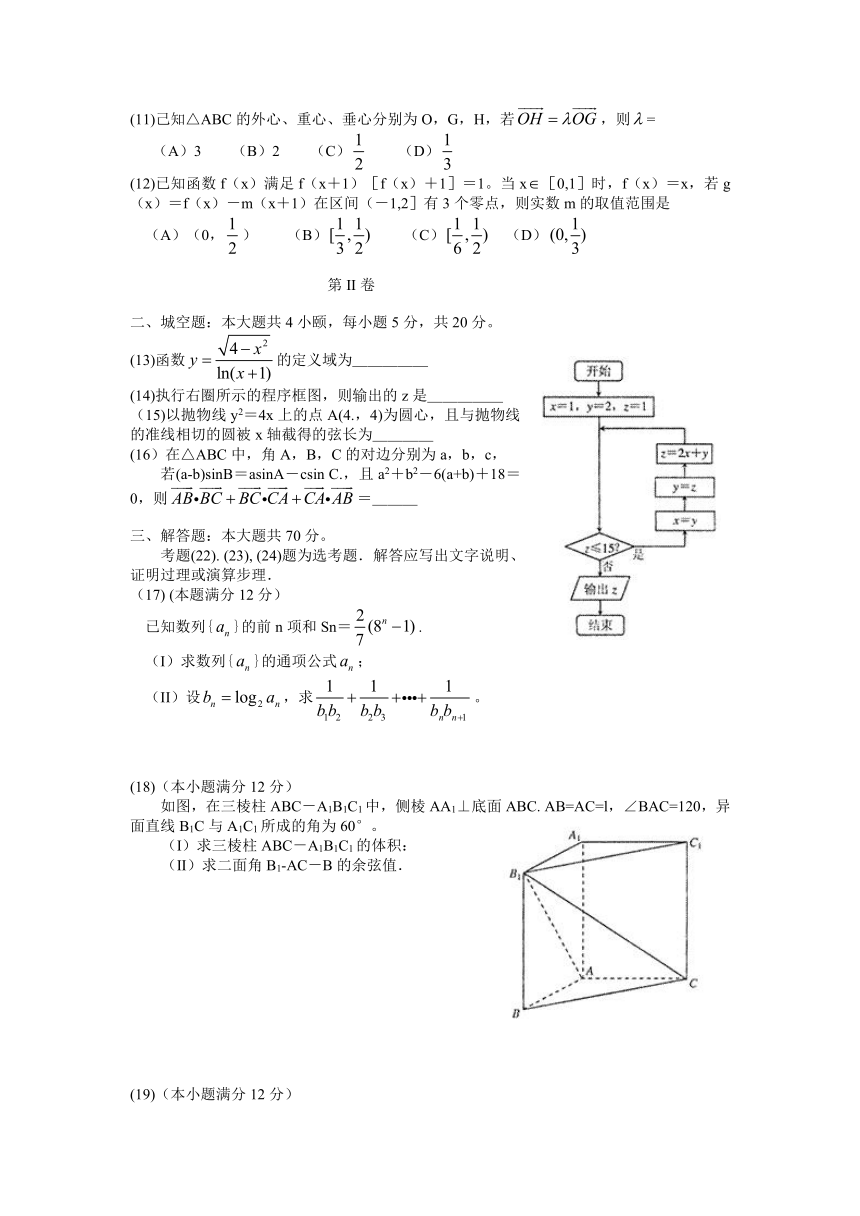
(14)执行右圈所示的程序框图,则输出的z是_____
(15)以抛物线y2=4x上的点A(4.,4)为圆心,且与抛物线的准线相切的圆被x轴截得的弦长为____
(16)在△ABC中,角A,B,C的对边分别为a,b,c,
若(a-b)sinB=asinA-csin C.,且a2+b2-6(a+b)+18=0,则=___
三、解答题:本大题共70分。
考题(22). (23), (24)题为选考题.解答应写出文字说明、证明过理或演算步理.
(17) (本题满分12分)
已知数列{}的前n项和Sn=.
(I)求数列{}的通项公式;
(II)设,求。
(18)(本小题满分12分)
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC. AB=AC=l,∠BAC=120,异面直线B1C与A1C1所成的角为60°。
(I)求三棱柱ABC-A1B1C1的体积:
(II)求二面角B1-AC-B的余弦值.
(19)(本小题满分12分)
某生产线生产的产品等级为随机变量X.,其分布列:
X 1 2 3
P 0.5 a b
设E(X)=1.7。
(I)求a. b的值
(II)已知出售一件1级,2级,3级该产品的利润依次为306元,100元,0元.在
该产品生产线上随机抽取两件产品并出售,设出售两件产品的利润之和为Y,求Y的分
布列和E(Y).
(20)(本小题满分12分)
设动点M(x, y)到直线y=3的距离与它到点F(0, 1)的距离之比为,点M的轨迹为曲线E.
(I)求曲线E的方程:
(II)过点F作直线l与曲线E交于A, B两点,且.当3时,求
直线l斜率k的取值范围·
(21)(本小胭满分12分)
已知函致f (x)=x3十bx2+cx+d.
(I)当b=0时,证明:曲线y=f(x)与其在点(0, f(0))处的切线只有一个公共点;
〔1()若曲线y=f(x)在点(1,f(1))处的切找为12x.+y-13=0,且它们只有一个公共
点,求函数y=f(x)的所有极值之和.
请考生在第(22), (23), (24)三题中任选一题作答,如果多做,则按所做的第一
题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
(22)(本小题清分10分)选修4-1几何证明选讲
如图,圆O的圆心O在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边
AC交于D,E,AD=DE=EC,AB=。
(I)求BC的长;
(II)求圆O的半径。
(24)(本小题满分IO分)选修4-5:不等式选讲
设f(x)=|x+1|一|x-2|.
(I)若不等式f(x)}≤a的解集为.求a的值;
(II)若R. f(x)十4m<m2,求m的取值范围.
唐山市2012—2013学年度高三年级摸底考试
理科数学参考答案
选择题:
A卷:ADCBD AABCC DB
B卷:CDABD ADBCB AC
二、填空题:
(13)(-1,0)∪(0,2] (14)17 (15)6 (16)-
三、解答题:
(17)解:
(Ⅰ)a1=S1=(81-1)=2. …1分
当n≥2时,an=Sn-Sn-1=(8n-1)-(8n-1-1)=23n-2.
当n=1时上式也成立,所以an=23n-2(n∈N*). …6分
(Ⅱ)由(Ⅰ)知,bn=log223n-2=3n-2, …7分
所以
++…+=++…+
=[(1-)+(-)+…+(-)]
=(1-)=. …12分
(18)解:
(Ⅰ)如图,以A为原点,AC为y轴,AA1为z轴,建立空间直角坐标系.
设AA1=a(a>0),依题意得
B1(,-,a),A(0,0,0),C(0,1,0).
=(-,,-a),
==(0,1,0),
由异面直线B1C与A1C1所成的角为60,知
|cos,|=
==,解得a=. …4分
所以三棱柱ABC-A1B1C1的体积
V=AB·ACsin120·AA1=×1×1××=. …6分
(Ⅱ)由(Ⅰ)知,=(-,,-).
设n=(x,y,z)为面ACB1的法向量,则n·=0,n·=0,
则
取z=1,得x=-2,于是n=(-2,0,1). …9分
又m=(0,0,1)为面ACB的一个法向量,
所以cosm,n==.
因此二面角B1-AC-B的余弦值为. …12分
(19)解:
(Ⅰ)依题意,
解得a=0.3,b=0.2. …4分
(Ⅱ)Y的所有可能取值为0,100,200,300,400,600.
P(Y=0)=0.22=0.04,P(Y=100)=C0.2×0.3=0.12,
P(Y=200)=0.32=0.09,P(Y=300)=C0.2×0.5=0.2,
P(Y=400)=C0.3×0.5=0.3,P(Y=600)=0.52=0.25. …8分
Y的分布列为
Y 0 100 200 300 400 600
P 0.04 0.12 0.09 0.2 0.3 0.25 …10分
E(Y)=0×0.04+100×0.12+200×0.09+300×0.2+400×0.3+600×0.25
=360(元). …12分
(20)解:
(
(21)解:
(Ⅰ)当b=0时,f(x)=x3+cx+d,f(x)=3x2+c.
f(0)=d,f(0)=c. …2分
曲线y=f(x)与其在点(0,f(0))处的切线为y=cx+d.
由消去y,得x3=0,x=0.
所以曲线y=f(x)与其在点(0,f(0))处的切线只有一个公共点即切点. …5分
(Ⅱ)由已知,切点为(1,1).
又f(x)=3x2+2bx+c,于是
即得c=-2b-15,d=b+15.
从而f(x)=x3+bx2-(2b+15)x+b+15. …8分
由消去y,得x3+bx2-(2b+3)x+b+2=0.
因直线12x+y-13=0与曲线y=f(x)只有一个公共点(1,1),
则方程x3+bx2-(2b+3)x+b+2=(x-1)[x2+(b+1)x-b-2]
=(x-1) (x-1) (x+b+2)
故b=-3. …10分
于是f(x)=x3-3x2-9x+12,f(x)=3x2-6x-9=3(x+1)(x-3).
当x变化时,f(x),f(x)的变化如下:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f(x) + 0 - 0 +
f(x) ↗ 极大值17 ↘ 极小值-15 ↗
由此知,函数y=f(x)的所有极值之和为2. …12分
(22)解:
(Ⅰ)由已知及由切割线定理,有AB2=AD·AE=AC·AC,
所以AC2=AB2. …3分
由勾股定理得,BC==7. …5分
(Ⅱ)设圆O与BC的交点为F,圆O的半径为r.
由割线定理,得CF·CB=CE·CD=AC·AC=AB2, …8分
即(7-2r)×7=14,解得r=. …10分
(23)解:
(Ⅰ)曲线C1的极坐标方程化为ρ=sinθ+cosθ,
两边同乘以ρ,得ρ2=ρsinθ+ρcosθ,
则曲线C1的直角坐标方程为x2+y2=y+x,即x2+y2-x-y=0. …3分
曲线C2的极坐标方程化为ρsinθ+ρcosθ=4,
则曲线C2的的直角坐标方程为y+x=4,即x+y-8=0. …6分
(Ⅱ)将曲线C1的直角坐标方程化为(x-)2+(y-)2=1,
它表示以(,)为圆心,以1为半径的圆.
该圆圆心到曲线C2即直线x+y-8=0的距离
d==3, …8分
所以|AB|的最小值为2. …10分
(24)解:
(Ⅰ)f(x)=其图象如下:
…3分
当x=时,f(x)=0.
当x<时,f(x)<0;当x>时,f(x)>0.
所以a=0. …6分
(Ⅱ)不等式f(x)+4m<m2,即f(x)<m2-4m.
因为f(x)的最小值为-3,所以问题等价于-3<m2-4m.
解得m<1,或m>3.
故m的取值范围是(-∞,1)∪(3,+∞). …10分
B
C
A
z
x
y
A
E
B
C
D
O
F
O
3
y
x
-3
2
-1
eq \f( 1 ,2)
-1
理科数学
第I卷
一、选择题(共60分)
(1)复数的虚部为
(A)2i (B)-2i (C)2 (D)-2
(2)设集合U=AUB, A={1,2,3}, AB={1},则=
(A){2} (B) {3} (C) {1,2,3} (D) {2,3}
(3)已知x,y满足,则z=2x-y的最大值为
lax-Y}-3,
(A) 2 (B)1 (C) -1 (D) 3
(4)已知双曲=1的离心串为2,则该双曲线的实轴长为
(A)2 (B)4 (C) 2 (D) 4
(5)若tnnθ=2,则cos2θ=
(A) (B)- (C) (D)-
(6)下列函数中,既是偶函数,又在区间(0. 3)内是增函数的是
(A) y= (B) y=coss
(C)y= (D) y=x+x-1
(7)在三棱锥P-ABC中,PA=PB=PC=,侧棱PA与底面ABC所成的角为60°,则该三棱锥外接球的体积为
(A)2 (B) (C)4 (D)
(8) 要得到函数的图象,只需将函数的图象
(A)向左平移个单位 (B)向右平移单位
(C)向左平移个单位 (D向右平移个单位
(9)空间几何体的三视图如图所示,则该几何体的表面积为
(A)6+2 (B)8+2
(C)8+2 (B)6+2
(10)一名小学生的年龄和身高(单位:cm)
的数据如下:
年龄x 6 7 8 9
身高y 118 126 136 144
由散点图可知,身高y与年龄x之间的线性回归直线方程为,预测该学生10岁时的身高为
(A) 154 .(B) 153 (C) 152 (D) 151
(11)己知△ABC的外心、重心、垂心分别为O,G,H,若,则=
(A)3 (B)2 (C) (D)
(12)已知函数f(x)满足f(x+1)[f(x)+1]=1。当x[0,1]时,f(x)=x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
(A)(0,) (B) (C) (D)
第II卷
二、城空题:本大题共4小颐,每小题5分,共20分。
(13)函数的定义域为_____
(14)执行右圈所示的程序框图,则输出的z是_____
(15)以抛物线y2=4x上的点A(4.,4)为圆心,且与抛物线的准线相切的圆被x轴截得的弦长为____
(16)在△ABC中,角A,B,C的对边分别为a,b,c,
若(a-b)sinB=asinA-csin C.,且a2+b2-6(a+b)+18=0,则=___
三、解答题:本大题共70分。
考题(22). (23), (24)题为选考题.解答应写出文字说明、证明过理或演算步理.
(17) (本题满分12分)
已知数列{}的前n项和Sn=.
(I)求数列{}的通项公式;
(II)设,求。
(18)(本小题满分12分)
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC. AB=AC=l,∠BAC=120,异面直线B1C与A1C1所成的角为60°。
(I)求三棱柱ABC-A1B1C1的体积:
(II)求二面角B1-AC-B的余弦值.
(19)(本小题满分12分)
某生产线生产的产品等级为随机变量X.,其分布列:
X 1 2 3
P 0.5 a b
设E(X)=1.7。
(I)求a. b的值
(II)已知出售一件1级,2级,3级该产品的利润依次为306元,100元,0元.在
该产品生产线上随机抽取两件产品并出售,设出售两件产品的利润之和为Y,求Y的分
布列和E(Y).
(20)(本小题满分12分)
设动点M(x, y)到直线y=3的距离与它到点F(0, 1)的距离之比为,点M的轨迹为曲线E.
(I)求曲线E的方程:
(II)过点F作直线l与曲线E交于A, B两点,且.当3时,求
直线l斜率k的取值范围·
(21)(本小胭满分12分)
已知函致f (x)=x3十bx2+cx+d.
(I)当b=0时,证明:曲线y=f(x)与其在点(0, f(0))处的切线只有一个公共点;
〔1()若曲线y=f(x)在点(1,f(1))处的切找为12x.+y-13=0,且它们只有一个公共
点,求函数y=f(x)的所有极值之和.
请考生在第(22), (23), (24)三题中任选一题作答,如果多做,则按所做的第一
题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
(22)(本小题清分10分)选修4-1几何证明选讲
如图,圆O的圆心O在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边
AC交于D,E,AD=DE=EC,AB=。
(I)求BC的长;
(II)求圆O的半径。
(24)(本小题满分IO分)选修4-5:不等式选讲
设f(x)=|x+1|一|x-2|.
(I)若不等式f(x)}≤a的解集为.求a的值;
(II)若R. f(x)十4m<m2,求m的取值范围.
唐山市2012—2013学年度高三年级摸底考试
理科数学参考答案
选择题:
A卷:ADCBD AABCC DB
B卷:CDABD ADBCB AC
二、填空题:
(13)(-1,0)∪(0,2] (14)17 (15)6 (16)-
三、解答题:
(17)解:
(Ⅰ)a1=S1=(81-1)=2. …1分
当n≥2时,an=Sn-Sn-1=(8n-1)-(8n-1-1)=23n-2.
当n=1时上式也成立,所以an=23n-2(n∈N*). …6分
(Ⅱ)由(Ⅰ)知,bn=log223n-2=3n-2, …7分
所以
++…+=++…+
=[(1-)+(-)+…+(-)]
=(1-)=. …12分
(18)解:
(Ⅰ)如图,以A为原点,AC为y轴,AA1为z轴,建立空间直角坐标系.
设AA1=a(a>0),依题意得
B1(,-,a),A(0,0,0),C(0,1,0).
=(-,,-a),
==(0,1,0),
由异面直线B1C与A1C1所成的角为60,知
|cos,|=
==,解得a=. …4分
所以三棱柱ABC-A1B1C1的体积
V=AB·ACsin120·AA1=×1×1××=. …6分
(Ⅱ)由(Ⅰ)知,=(-,,-).
设n=(x,y,z)为面ACB1的法向量,则n·=0,n·=0,
则
取z=1,得x=-2,于是n=(-2,0,1). …9分
又m=(0,0,1)为面ACB的一个法向量,
所以cosm,n==.
因此二面角B1-AC-B的余弦值为. …12分
(19)解:
(Ⅰ)依题意,
解得a=0.3,b=0.2. …4分
(Ⅱ)Y的所有可能取值为0,100,200,300,400,600.
P(Y=0)=0.22=0.04,P(Y=100)=C0.2×0.3=0.12,
P(Y=200)=0.32=0.09,P(Y=300)=C0.2×0.5=0.2,
P(Y=400)=C0.3×0.5=0.3,P(Y=600)=0.52=0.25. …8分
Y的分布列为
Y 0 100 200 300 400 600
P 0.04 0.12 0.09 0.2 0.3 0.25 …10分
E(Y)=0×0.04+100×0.12+200×0.09+300×0.2+400×0.3+600×0.25
=360(元). …12分
(20)解:
(
(21)解:
(Ⅰ)当b=0时,f(x)=x3+cx+d,f(x)=3x2+c.
f(0)=d,f(0)=c. …2分
曲线y=f(x)与其在点(0,f(0))处的切线为y=cx+d.
由消去y,得x3=0,x=0.
所以曲线y=f(x)与其在点(0,f(0))处的切线只有一个公共点即切点. …5分
(Ⅱ)由已知,切点为(1,1).
又f(x)=3x2+2bx+c,于是
即得c=-2b-15,d=b+15.
从而f(x)=x3+bx2-(2b+15)x+b+15. …8分
由消去y,得x3+bx2-(2b+3)x+b+2=0.
因直线12x+y-13=0与曲线y=f(x)只有一个公共点(1,1),
则方程x3+bx2-(2b+3)x+b+2=(x-1)[x2+(b+1)x-b-2]
=(x-1) (x-1) (x+b+2)
故b=-3. …10分
于是f(x)=x3-3x2-9x+12,f(x)=3x2-6x-9=3(x+1)(x-3).
当x变化时,f(x),f(x)的变化如下:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f(x) + 0 - 0 +
f(x) ↗ 极大值17 ↘ 极小值-15 ↗
由此知,函数y=f(x)的所有极值之和为2. …12分
(22)解:
(Ⅰ)由已知及由切割线定理,有AB2=AD·AE=AC·AC,
所以AC2=AB2. …3分
由勾股定理得,BC==7. …5分
(Ⅱ)设圆O与BC的交点为F,圆O的半径为r.
由割线定理,得CF·CB=CE·CD=AC·AC=AB2, …8分
即(7-2r)×7=14,解得r=. …10分
(23)解:
(Ⅰ)曲线C1的极坐标方程化为ρ=sinθ+cosθ,
两边同乘以ρ,得ρ2=ρsinθ+ρcosθ,
则曲线C1的直角坐标方程为x2+y2=y+x,即x2+y2-x-y=0. …3分
曲线C2的极坐标方程化为ρsinθ+ρcosθ=4,
则曲线C2的的直角坐标方程为y+x=4,即x+y-8=0. …6分
(Ⅱ)将曲线C1的直角坐标方程化为(x-)2+(y-)2=1,
它表示以(,)为圆心,以1为半径的圆.
该圆圆心到曲线C2即直线x+y-8=0的距离
d==3, …8分
所以|AB|的最小值为2. …10分
(24)解:
(Ⅰ)f(x)=其图象如下:
…3分
当x=时,f(x)=0.
当x<时,f(x)<0;当x>时,f(x)>0.
所以a=0. …6分
(Ⅱ)不等式f(x)+4m<m2,即f(x)<m2-4m.
因为f(x)的最小值为-3,所以问题等价于-3<m2-4m.
解得m<1,或m>3.
故m的取值范围是(-∞,1)∪(3,+∞). …10分
B
C
A
z
x
y
A
E
B
C
D
O
F
O
3
y
x
-3
2
-1
eq \f( 1 ,2)
-1
同课章节目录
