八年级数学12.2.1作轴对称图形第1课时1
文档属性
| 名称 | 八年级数学12.2.1作轴对称图形第1课时1 |

|
|
| 格式 | zip | ||
| 文件大小 | 592.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-18 11:30:42 | ||
图片预览






文档简介
(共22张PPT)
12.2.1
作轴对称图形①
学习 目标
1.理解轴对称变换的定义。
2.利用轴对称变换设计图案。
3.作一个图形关于一条直线的轴对称图形 。
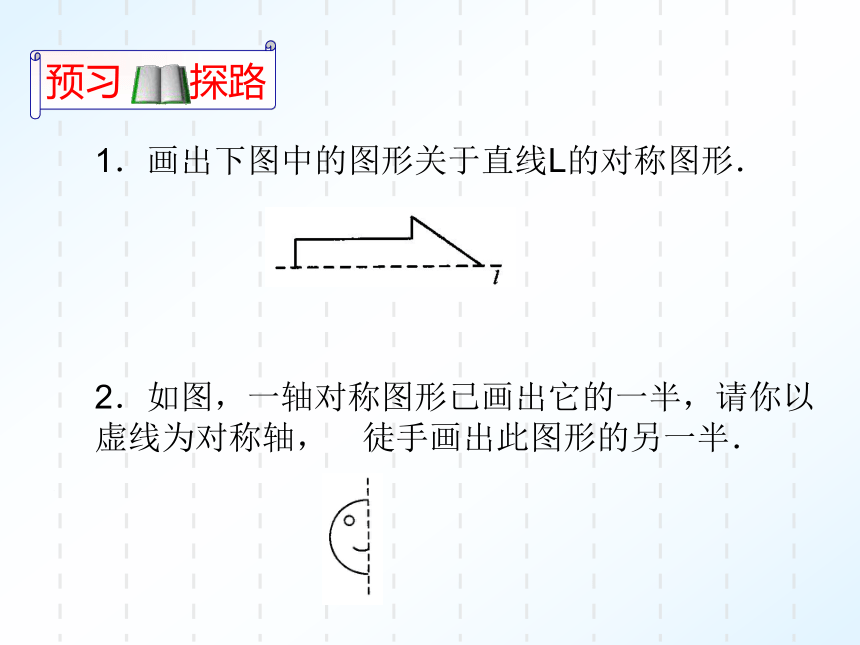
预习 探路
1.画出下图中的图形关于直线L的对称图形.
2.如图,一轴对称图形已画出它的一半,请你以虚线为对称轴,徒手画出此图形的另一半.
如果你是设计
师,你能设计出
轴对称图案吗
创设情境
问题1:在一张半透明的左边部分画一只
左脚印。
⑵ 左脚印与右脚印有何关系
折痕所在的直线是什么
⑶连接任意一对对应点所得线
段与折痕是怎样的位置关系
⑴ 如何得到相应的右脚印
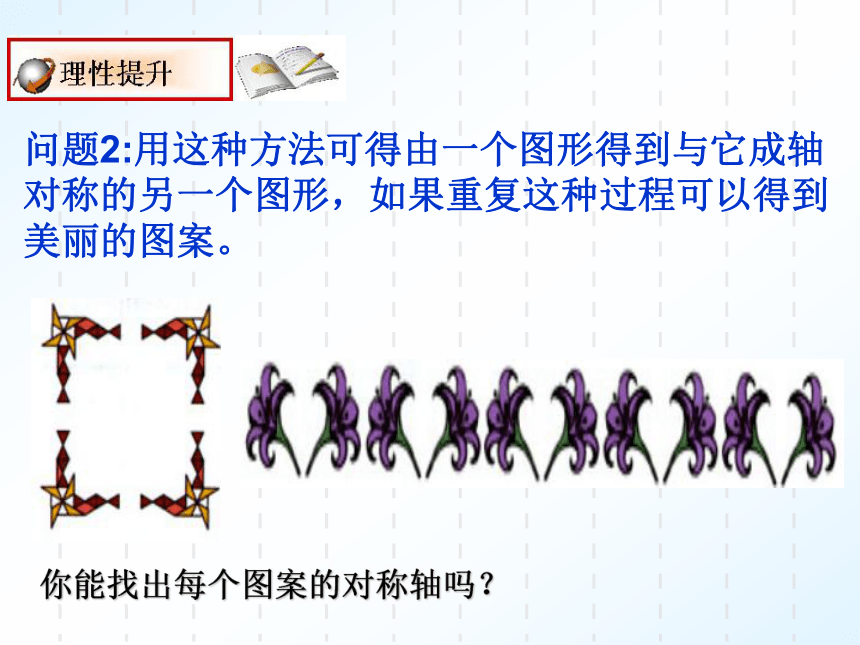
问题2:用这种方法可得由一个图形得到与它成轴对称的另一个图形,如果重复这种过程可以得到美丽的图案。
你能找出每个图案的对称轴吗?
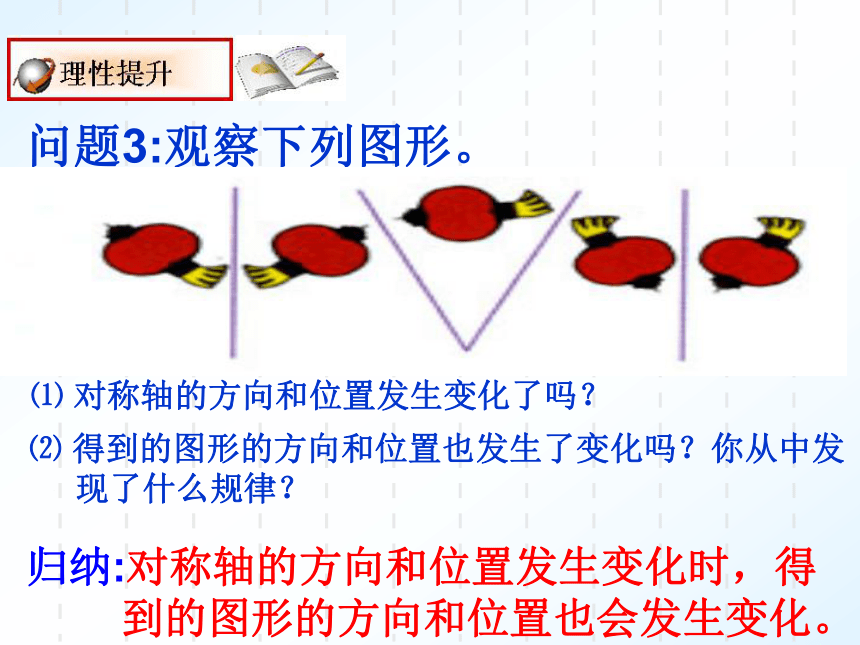
问题3:观察下列图形。
⑴ 对称轴的方向和位置发生变化了吗?
⑵ 得到的图形的方向和位置也发生了变化吗?你从中发
现了什么规律?
归纳:对称轴的方向和位置发生变化时,得
到的图形的方向和位置也会发生变化。
问题4:
自己动手在一张半透明的纸上画一个你最喜欢的图形,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置,并重复几次,你又得到了什么?
问题5:
⑴ 像这样由一个平面图形得到它
的轴对称图形叫轴对称变换。
⑵ 轴对称变换性质:
① 由一个平面图形可以得到它
关于一条直线l对称的图形,这
个图形与原图形的形状、大小
完全一样(即全等)。
② 新图形上的每一点,都是原图形上的某
一点关于直线l的对称点。
③ 连接任何一对对应点的线段被对称轴垂
直平分。
小结归纳
1
轴对称图形和轴对称变换
区别: 轴对称图形讲的是一个图形两部分的
位置关系,是一个静止状态。而轴对称
变换是一种变换,讲的是一个图形得
到与它轴对称的图形的过程。
联系:① 它们都是沿一条直线对折能完全重合。
② 成轴对称的两个图形中的任何一个可
以看作由另一个图形经过轴对称变换
后得到。一个轴对称图形也可以看作
以它的一部分为基础,经过轴对称变
换扩展而成的。
问题:如图,已知△ABC和直线l,作出与
△ABC关于直线l成轴对称的图形。
⑴ △ABC关于直线l的对称图形是
什么形状?
⑵ △ABC的轴对称图形可以由哪
几个点确定?
⑶ 在△ABC上,取哪几个点作出
其关于l的对称点?
⑷ 如何作一个已知点关于直线的
对称点?
l
随堂练习
随堂练习
B
C
A
Aˊ
Bˊ
Cˊ
o
l
随堂练习
归纳:几何图形都可以看
作由点组成,我们只要分
别作出这些点关于对称
轴的对应点,再连接
这些对应点,就可以得
到原图形的轴对称图形。
对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点的对称点,连接这些对称点,就可以得到原图形的轴对称图形(即①找点→②作垂线→③
倍长→④连接)。
B
C
A
Aˊ
Bˊ
Cˊ
o
l
随堂练习
练一练: ⑴ 如图
把下列图形补成关于直线l对称的图形。
A
B
C
D
E
C
B
A
D
E
l
1. (2010.甘肃) (6分)图①、图②均为7×6的正方形网格,点A、B、C在格点(小正方形的顶点)上.
(1)在图①中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;
中考链接
1
A
B
D
A
B
C
D
C
中考链接
1
(2010.江津)如图,有分别过A、B两个加油站的公路、相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且P到两条公路、的距离也相等。请用尺规作图作出点P(不写作法,保留作图痕迹).
当堂测试
轴对称变换后的图形
原来的图形
当堂测试
猜单词游戏
1、
6、
5、
3、
2、
4、
轴对称变换后的图形
原来的图形
小结归纳
2
通过本节课的学习,你有哪些收获?
1、轴对称变换的定义;
3、画已知图形关于已知直线的对称图形
2、轴对称变换的特征;
由一个平面图形得到它的轴对称图形叫做轴对称变换。
小结归纳
2
1、由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;
2、新图形上的每一点,都是原图形上的某一点关于直线l的对称点;
3、连接任意一对对应点的线段被对称轴垂直平分。
轴对称变换的特征:
小结归纳
2
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点);
(作特殊点关于已知直线的对称点);
(连接对称点)。
12.2.1
作轴对称图形①
学习 目标
1.理解轴对称变换的定义。
2.利用轴对称变换设计图案。
3.作一个图形关于一条直线的轴对称图形 。
预习 探路
1.画出下图中的图形关于直线L的对称图形.
2.如图,一轴对称图形已画出它的一半,请你以虚线为对称轴,徒手画出此图形的另一半.
如果你是设计
师,你能设计出
轴对称图案吗
创设情境
问题1:在一张半透明的左边部分画一只
左脚印。
⑵ 左脚印与右脚印有何关系
折痕所在的直线是什么
⑶连接任意一对对应点所得线
段与折痕是怎样的位置关系
⑴ 如何得到相应的右脚印
问题2:用这种方法可得由一个图形得到与它成轴对称的另一个图形,如果重复这种过程可以得到美丽的图案。
你能找出每个图案的对称轴吗?
问题3:观察下列图形。
⑴ 对称轴的方向和位置发生变化了吗?
⑵ 得到的图形的方向和位置也发生了变化吗?你从中发
现了什么规律?
归纳:对称轴的方向和位置发生变化时,得
到的图形的方向和位置也会发生变化。
问题4:
自己动手在一张半透明的纸上画一个你最喜欢的图形,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置,并重复几次,你又得到了什么?
问题5:
⑴ 像这样由一个平面图形得到它
的轴对称图形叫轴对称变换。
⑵ 轴对称变换性质:
① 由一个平面图形可以得到它
关于一条直线l对称的图形,这
个图形与原图形的形状、大小
完全一样(即全等)。
② 新图形上的每一点,都是原图形上的某
一点关于直线l的对称点。
③ 连接任何一对对应点的线段被对称轴垂
直平分。
小结归纳
1
轴对称图形和轴对称变换
区别: 轴对称图形讲的是一个图形两部分的
位置关系,是一个静止状态。而轴对称
变换是一种变换,讲的是一个图形得
到与它轴对称的图形的过程。
联系:① 它们都是沿一条直线对折能完全重合。
② 成轴对称的两个图形中的任何一个可
以看作由另一个图形经过轴对称变换
后得到。一个轴对称图形也可以看作
以它的一部分为基础,经过轴对称变
换扩展而成的。
问题:如图,已知△ABC和直线l,作出与
△ABC关于直线l成轴对称的图形。
⑴ △ABC关于直线l的对称图形是
什么形状?
⑵ △ABC的轴对称图形可以由哪
几个点确定?
⑶ 在△ABC上,取哪几个点作出
其关于l的对称点?
⑷ 如何作一个已知点关于直线的
对称点?
l
随堂练习
随堂练习
B
C
A
Aˊ
Bˊ
Cˊ
o
l
随堂练习
归纳:几何图形都可以看
作由点组成,我们只要分
别作出这些点关于对称
轴的对应点,再连接
这些对应点,就可以得
到原图形的轴对称图形。
对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点的对称点,连接这些对称点,就可以得到原图形的轴对称图形(即①找点→②作垂线→③
倍长→④连接)。
B
C
A
Aˊ
Bˊ
Cˊ
o
l
随堂练习
练一练: ⑴ 如图
把下列图形补成关于直线l对称的图形。
A
B
C
D
E
C
B
A
D
E
l
1. (2010.甘肃) (6分)图①、图②均为7×6的正方形网格,点A、B、C在格点(小正方形的顶点)上.
(1)在图①中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;
中考链接
1
A
B
D
A
B
C
D
C
中考链接
1
(2010.江津)如图,有分别过A、B两个加油站的公路、相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且P到两条公路、的距离也相等。请用尺规作图作出点P(不写作法,保留作图痕迹).
当堂测试
轴对称变换后的图形
原来的图形
当堂测试
猜单词游戏
1、
6、
5、
3、
2、
4、
轴对称变换后的图形
原来的图形
小结归纳
2
通过本节课的学习,你有哪些收获?
1、轴对称变换的定义;
3、画已知图形关于已知直线的对称图形
2、轴对称变换的特征;
由一个平面图形得到它的轴对称图形叫做轴对称变换。
小结归纳
2
1、由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;
2、新图形上的每一点,都是原图形上的某一点关于直线l的对称点;
3、连接任意一对对应点的线段被对称轴垂直平分。
轴对称变换的特征:
小结归纳
2
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点);
(作特殊点关于已知直线的对称点);
(连接对称点)。
