八年级数学12.2.2用坐标表示轴对称
文档属性
| 名称 | 八年级数学12.2.2用坐标表示轴对称 |

|
|
| 格式 | zip | ||
| 文件大小 | 143.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-18 11:31:41 | ||
图片预览



文档简介
(共20张PPT)
12.2.2
用坐标表示轴对称
学习 目标
1.能够利用x轴和y轴对称的点的规律,作出关 于x轴和y轴对称的图形。
2.通过引导学生在实践活动中探究,发现在平面直角坐标系中,关于x轴和y轴对称的点的规律,从而发展学生的数形结合的思想,激发他们的求知欲和好奇心。
预习 探路
1、点 P(-5, 6)与点 Q关于x轴对称,则点 Q的坐标为__________.
2、点 M (a, -5)与点 N(-2, b)关于x轴对称,则a=_____, b =_____.
(- 5 , -6 )
-2
5
3、点 P(-5, 6)与点 Q关于y轴对称,则点 Q的
坐标为__________.
4、点 M(a, -5)与点 N(-2, b)关于y轴对称,则a=_____, b =_____.
( 5 , 6 )
2
-5
创设情境
0
1
2
3
4
5
-4
-3
-2
-1
x
·
·
·
·
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
y
·
·
A1
B1
D1
C1
·
·
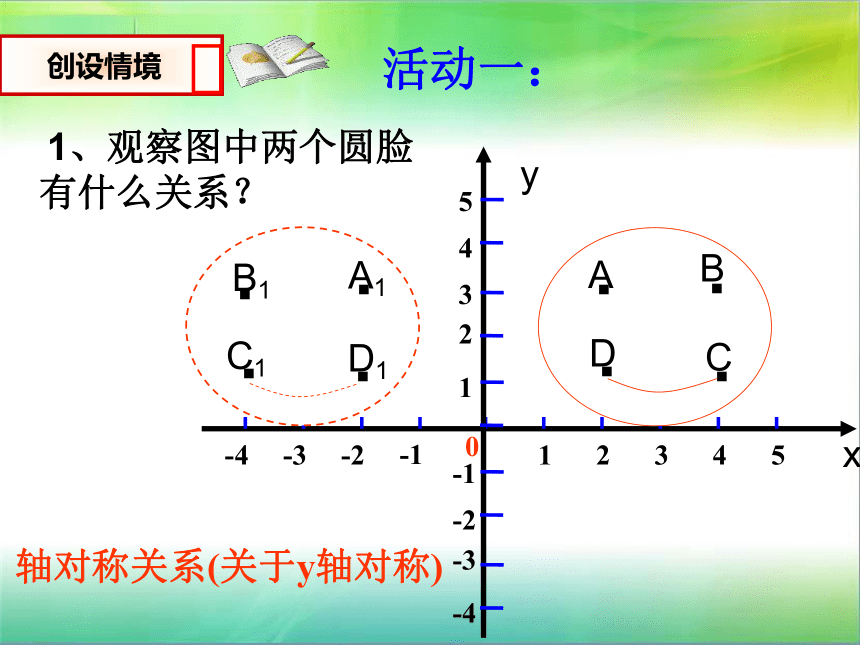
1、观察图中两个圆脸有什么关系?
轴对称关系(关于y轴对称)
活动一:
创设情境
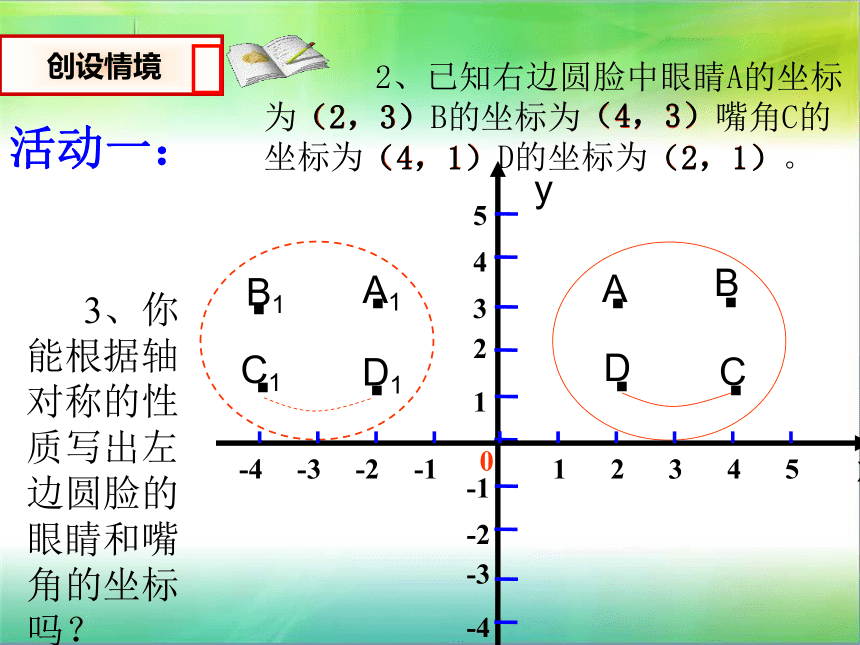
2、已知右边圆脸中眼睛A的坐标为(2,3)B的坐标为(4,3)嘴角C的坐标为(4,1)D的坐标为(2,1)。
·
·
·
·
A
B
C
D
·
·
A1
B1
D1
C1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
3、你能根据轴对称的性质写出左边圆脸的眼睛和嘴角的坐标吗?
(2,3)
(4,3)
(4,1)
(2,1)
活动一:
创设情境
·
·
·
·
A
B
C
D
·
·
A1
B1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
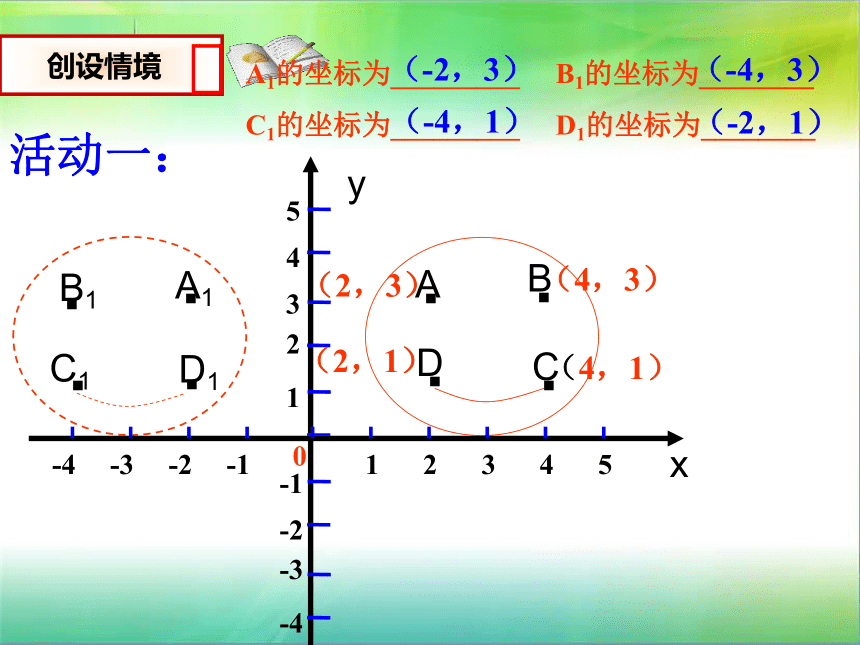
A1的坐标为_________ B1的坐标为________
C1的坐标为_________ D1的坐标为________
(-2,3)
(-4,3)
(-4,1)
(-2,1)
C1
D1
(4,3)
(2,3)
(4,1)
(2,1)
活动一:
创设情境
活动二:
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
.
(2,2)
.
(4,2)
.
(4,4)
.
(2,4)
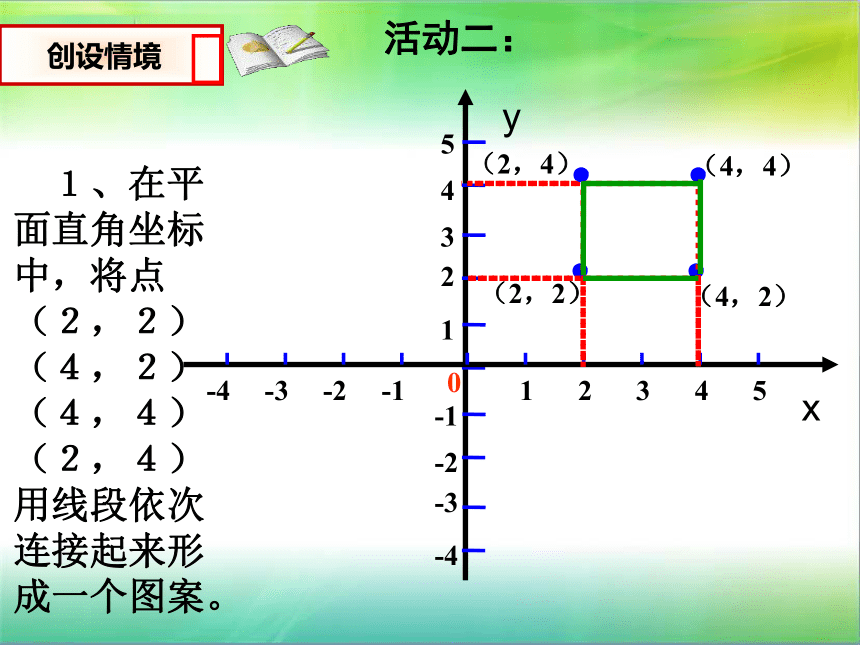
1、在平面直角坐标中,将点(2,2) (4,2)(4,4)(2,4)用线段依次连接起来形成一个图案。
活动二:
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
.
.
.
.
(2,2)
(4,2)
(4,4)
(2,4)
(-2,2)
(-2,4)
(-4,2)
(-4,4)
2、 纵坐标不变,横坐标分别乘以-1,再将所的各个点 用线段依次连接来,所得的图案与原图相比有何变化?
?
创设情境
活动二:
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
(4,4)
(2,4)
(4,2)
(2,2)
.
.
.
.
(2,-2)
(4,-4)
(2,-4)
(4,-2)
3、 横坐标不变,纵坐标分别乘以-1,再
将所的各个点用线段依次连接来,所得的图案与原图相比有何变化?
创设情境
创设情境
活动一:
原图 (2,2) (4,2) (4,4) (2,4)
原图 A(2,3) B(4,3) C(4,1) D(2,1)
A1(-2,3)
B1(-4,3)
C1(-4,3)
D1(-2,1)
关于y轴对称
活动二:
关于y轴对称
(-2,2)
(-2,2)
(-2,2)
(-2,2)
1、纵坐标不变,横坐标乘以-1
2、横坐标不变,纵坐标乘以-1
原图 (2,2) (4,2) (4,4) (2,4)
(2,-2)
(4,-2)
(4,-4)
(2,-4)
关于x轴对称
提问:从上面三个活动中你能得出关于x轴(y轴)对称的点具有什么规律?
(一)引导学生从活动中归纳:关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数。
(二)引导学生从活动中归纳:关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等。
例:已知△ABC的三个顶点 的坐标分别为A(-3,5), B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形。
方法构想
1、在平面直角坐标系中,点 (x,y)关于直线x=1对称点的坐标是多少
2、在平面直角坐标系中,点 (x,y)关于直线x=-1对称点的坐标是多少
3、在平面直角坐标系中,点 (x,y)关于直线y=1对称点的坐标是多少
4、在平面直角坐标系中,点 (x,y)关于直线y=-1对称点的坐标是多少
(-x+2,y)
(-x-2,y)
(x,-y+2)
(x,-y-2)
小结归纳
1
1.关于x轴对称的点 横坐标相等,纵坐标互为相反数。关于y轴对称的点 横坐标互为相反数,纵坐标相等。.
2.关于某条直线对称,可直接作图分析,不要死记硬背,建立坐标系就可完成.
随堂练习
1、教材P44练习第1、2、3题
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=____ b=_____
若点p与点p’关于y轴对称,则a=____ b=_____
4
6
-20
2
1.(2010.江津)已知点P(a,3)、Q(-2,b)关于轴对称,则a= ,b= .
中考链接
1
2. (2010.南通)在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有 ( )
A.5个 B.4个 C.3个 D.2个
B
-2
-3
当堂测试
1.若点P(-2,-5),Q(x,y)关于y轴对称,则x=______,y=______.
2.由(-1,4)→(-1,-4)经过了______变换,由(-5,-6)→(-5,-2)经过了_______变换.
-5
2
轴对称
平移
3.已知:点A(x,4-y),B(1-y,2x)关于y轴对称,求x-2y的值.
x-2y=1-2×2=-3
小结归纳
2
通过本节课的学习,你有哪些收获?
1、学习了在平面直角坐标系中,关于x轴和y轴对称 的点 的坐标的特点。
关于x轴对称的点横坐标相等,纵坐标互为相反数。关于y轴对称的点横坐标互为相反数,纵坐标相等。
2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形。
先求出已知图形中的一些特殊点(如多边形的顶点)的对应
点的坐标,描出并连接这些点,就可以得到这个图形的轴对
称图形.
独立
作业
教材P45 2,3,4题
12.2.2
用坐标表示轴对称
学习 目标
1.能够利用x轴和y轴对称的点的规律,作出关 于x轴和y轴对称的图形。
2.通过引导学生在实践活动中探究,发现在平面直角坐标系中,关于x轴和y轴对称的点的规律,从而发展学生的数形结合的思想,激发他们的求知欲和好奇心。
预习 探路
1、点 P(-5, 6)与点 Q关于x轴对称,则点 Q的坐标为__________.
2、点 M (a, -5)与点 N(-2, b)关于x轴对称,则a=_____, b =_____.
(- 5 , -6 )
-2
5
3、点 P(-5, 6)与点 Q关于y轴对称,则点 Q的
坐标为__________.
4、点 M(a, -5)与点 N(-2, b)关于y轴对称,则a=_____, b =_____.
( 5 , 6 )
2
-5
创设情境
0
1
2
3
4
5
-4
-3
-2
-1
x
·
·
·
·
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
y
·
·
A1
B1
D1
C1
·
·
1、观察图中两个圆脸有什么关系?
轴对称关系(关于y轴对称)
活动一:
创设情境
2、已知右边圆脸中眼睛A的坐标为(2,3)B的坐标为(4,3)嘴角C的坐标为(4,1)D的坐标为(2,1)。
·
·
·
·
A
B
C
D
·
·
A1
B1
D1
C1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
3、你能根据轴对称的性质写出左边圆脸的眼睛和嘴角的坐标吗?
(2,3)
(4,3)
(4,1)
(2,1)
活动一:
创设情境
·
·
·
·
A
B
C
D
·
·
A1
B1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
A1的坐标为_________ B1的坐标为________
C1的坐标为_________ D1的坐标为________
(-2,3)
(-4,3)
(-4,1)
(-2,1)
C1
D1
(4,3)
(2,3)
(4,1)
(2,1)
活动一:
创设情境
活动二:
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
.
(2,2)
.
(4,2)
.
(4,4)
.
(2,4)
1、在平面直角坐标中,将点(2,2) (4,2)(4,4)(2,4)用线段依次连接起来形成一个图案。
活动二:
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
.
.
.
.
(2,2)
(4,2)
(4,4)
(2,4)
(-2,2)
(-2,4)
(-4,2)
(-4,4)
2、 纵坐标不变,横坐标分别乘以-1,再将所的各个点 用线段依次连接来,所得的图案与原图相比有何变化?
?
创设情境
活动二:
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
(4,4)
(2,4)
(4,2)
(2,2)
.
.
.
.
(2,-2)
(4,-4)
(2,-4)
(4,-2)
3、 横坐标不变,纵坐标分别乘以-1,再
将所的各个点用线段依次连接来,所得的图案与原图相比有何变化?
创设情境
创设情境
活动一:
原图 (2,2) (4,2) (4,4) (2,4)
原图 A(2,3) B(4,3) C(4,1) D(2,1)
A1(-2,3)
B1(-4,3)
C1(-4,3)
D1(-2,1)
关于y轴对称
活动二:
关于y轴对称
(-2,2)
(-2,2)
(-2,2)
(-2,2)
1、纵坐标不变,横坐标乘以-1
2、横坐标不变,纵坐标乘以-1
原图 (2,2) (4,2) (4,4) (2,4)
(2,-2)
(4,-2)
(4,-4)
(2,-4)
关于x轴对称
提问:从上面三个活动中你能得出关于x轴(y轴)对称的点具有什么规律?
(一)引导学生从活动中归纳:关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数。
(二)引导学生从活动中归纳:关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等。
例:已知△ABC的三个顶点 的坐标分别为A(-3,5), B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形。
方法构想
1、在平面直角坐标系中,点 (x,y)关于直线x=1对称点的坐标是多少
2、在平面直角坐标系中,点 (x,y)关于直线x=-1对称点的坐标是多少
3、在平面直角坐标系中,点 (x,y)关于直线y=1对称点的坐标是多少
4、在平面直角坐标系中,点 (x,y)关于直线y=-1对称点的坐标是多少
(-x+2,y)
(-x-2,y)
(x,-y+2)
(x,-y-2)
小结归纳
1
1.关于x轴对称的点 横坐标相等,纵坐标互为相反数。关于y轴对称的点 横坐标互为相反数,纵坐标相等。.
2.关于某条直线对称,可直接作图分析,不要死记硬背,建立坐标系就可完成.
随堂练习
1、教材P44练习第1、2、3题
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=____ b=_____
若点p与点p’关于y轴对称,则a=____ b=_____
4
6
-20
2
1.(2010.江津)已知点P(a,3)、Q(-2,b)关于轴对称,则a= ,b= .
中考链接
1
2. (2010.南通)在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有 ( )
A.5个 B.4个 C.3个 D.2个
B
-2
-3
当堂测试
1.若点P(-2,-5),Q(x,y)关于y轴对称,则x=______,y=______.
2.由(-1,4)→(-1,-4)经过了______变换,由(-5,-6)→(-5,-2)经过了_______变换.
-5
2
轴对称
平移
3.已知:点A(x,4-y),B(1-y,2x)关于y轴对称,求x-2y的值.
x-2y=1-2×2=-3
小结归纳
2
通过本节课的学习,你有哪些收获?
1、学习了在平面直角坐标系中,关于x轴和y轴对称 的点 的坐标的特点。
关于x轴对称的点横坐标相等,纵坐标互为相反数。关于y轴对称的点横坐标互为相反数,纵坐标相等。
2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形。
先求出已知图形中的一些特殊点(如多边形的顶点)的对应
点的坐标,描出并连接这些点,就可以得到这个图形的轴对
称图形.
独立
作业
教材P45 2,3,4题
