三角形面积背景下得直线解析式问题

(共11张PPT)
三角形面积背景下的直线解析式问题
课程标准浙教版实验教科书
八年级
知识回顾
A
B
O
x
y
1
2
3
-1
-2
3
1
2
-1
-2
4
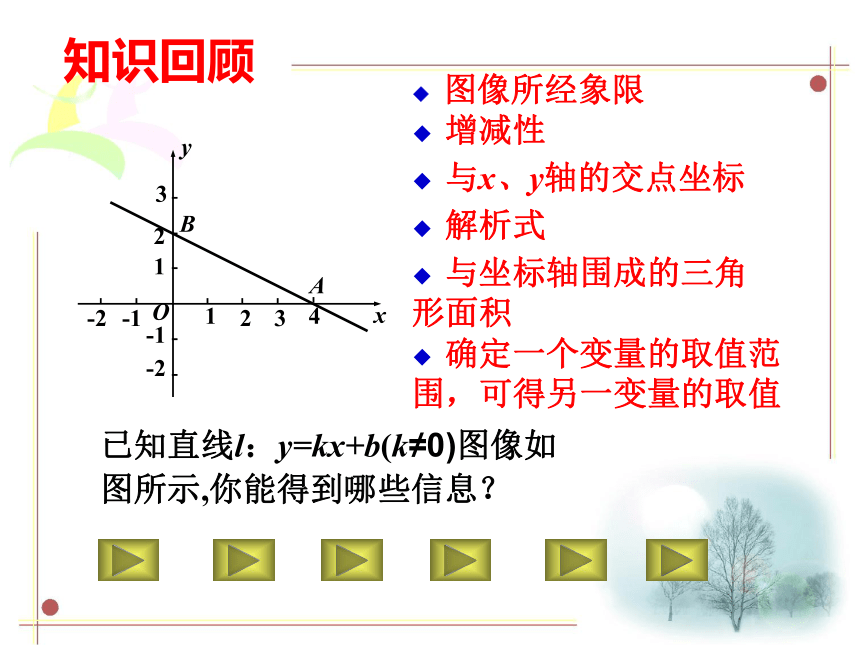
已知直线l：y=kx+b(k≠0)图像如图所示,你能得到哪些信息？
◆ 图像所经象限
◆ 增减性
◆ 与x、y轴的交点坐标
◆ 解析式
◆ 与坐标轴围成的三角 形面积
◆ 确定一个变量的取值范围，可得另一变量的取值
1. 已知直线y= -2x+4上有一点A（k,2），则k=
2. 正比例函数图像过点（2，-6），解析式为
3.直线l经过（-1，4）、 （-2，2），求：
①解析式；
②直线l与两坐标轴的交点坐标；
③直线l与坐标轴围成的三角形面积.
1
y= -3x
知识检验
O
x
y
1
-1
1
y=2x+6
A(-3 ，0) ，B(0，6)
S△AOB = 9
6
-3
A
B
待定系数法
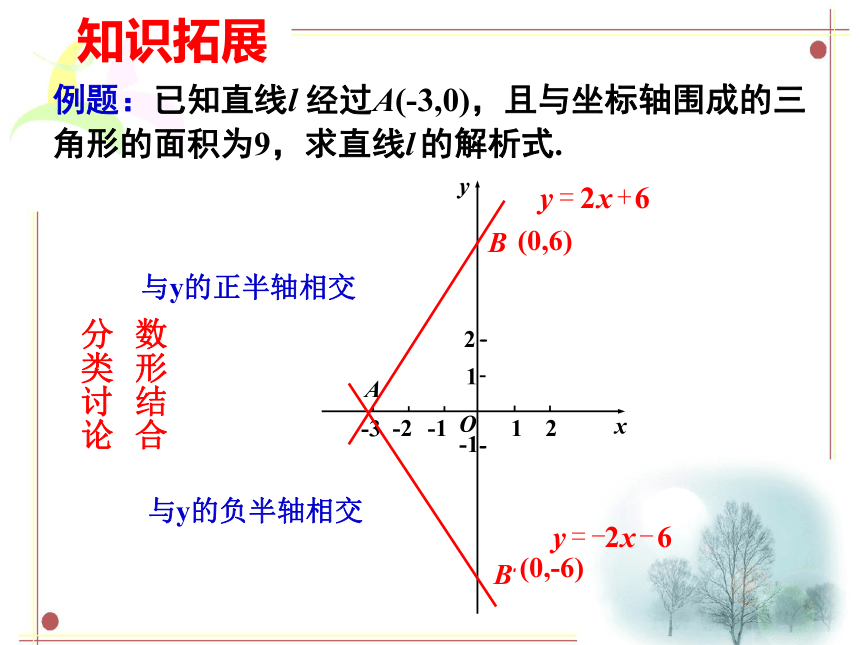
例题：已知直线l 经过A(-3,0)，且与坐标轴围成的三角形的面积为9，求直线l 的解析式.
A
O
x
y
1
2
-1
-2
1
2
-1
-3
B
B′
(0,-6)
(0,6)
知识拓展
与y的正半轴相交
与y的负半轴相交
分类讨论
数形结合
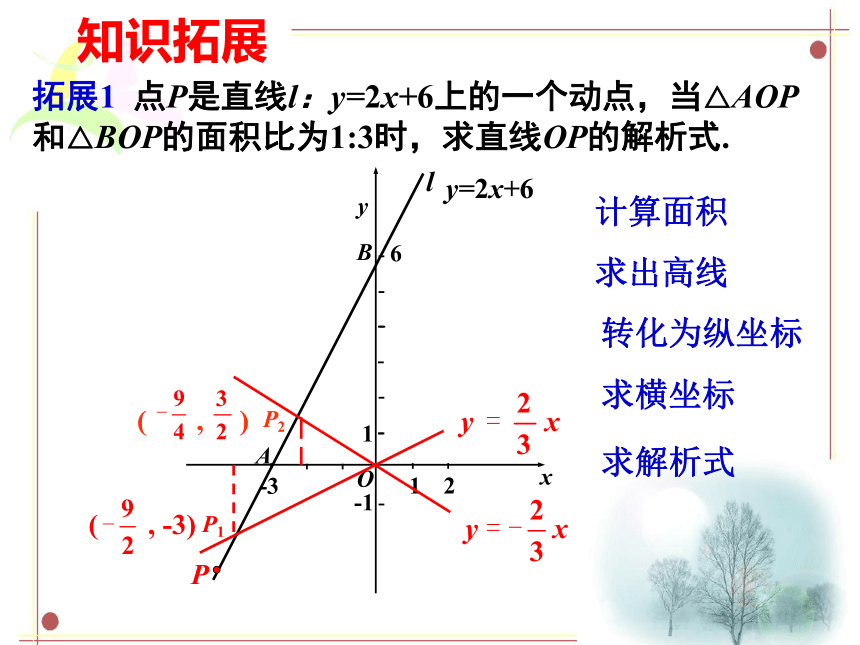
拓展1 点P是直线l：y=2x+6上的一个动点，当△AOP和△BOP的面积比为1:3时，求直线OP的解析式.
B
A
O
x
y
1
2
1
-1
-3
6
l
P1
P2
y=2x+6
( , -3)
知识拓展
P
( , )
计算面积
求出高线
转化为纵坐标
求横坐标
求解析式
拓展2 点Q是直线l：y=2x+6上的一个动点，若直线OQ、直线l与坐标轴所围成的三角形面积为△AOB的面积的一半，求直线OQ的解析式.
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
Q1
Q2
Q3
Q3( 1.5 , 9)
Q2 (-1.5 , 3)
( ,-3)
y=2x+6
-4.5
知识拓展
l
1. 这节课你学到了哪些数学思想？
交流提升
2. 如何利用面积求解析式？
分类讨论 数形结合
计算面积
求出高线
化纵坐标(或横坐标)
求横坐标(或纵坐标)
求解析式
拓展3 如图，以AO、OB为相邻两边补成一个长方形AOBC，若直线l1经过△AOB的某个顶点，且把长方形AOBC的面积分为1:2两部分，求直线l1的解析式.
当直线l1过点O时:
当直线l1过点B时:
当直线l1过点A时:
Q2
Q1
Q1 (-3,4)
Q2 (-2, 6)
Q3 (-2,0)
Q4 (-3, 2)
Q4
Q3
Q5 (-1,6)
Q6 (0, 4)
Q6
Q5
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
C
N
深化探究
y=2x+6
l
四边形 三角形
M
C
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
当直线l1过点O时:
当直线l1过点B时:
当直线l1过点A时:
Q2
Q1
Q1 (1,6)
Q2 (-1, 4)
Q3 (1,2)
Q4 (-1, 0)
Q4
Q3
Q5 (2,6)
Q6 (2, 4)
Q6
Q5
拓展4 如图，以AO、AB为邻边补成一个平行四边形AOCB，若直线l1经过△AOB的某个顶点,且把平行四边形AOCB的面积分为1:2两部分，求直线l1的解析式.
深化探究
y=2x+6
l