4.2 视图 课件(共32张PPT)
图片预览







文档简介
(共32张PPT)
第四章 投影与视图
2 视图
知识点一 三视图及常见几何体的三视图
1.三视图的定义
在实际生活中,人们常常从正面、左面和上面三个不同的方向观察一个物体,分别得到这个物体的三种视图,这样大体上就把一个物体的形状特征用平面图形表示出来了.
通常我们把从正面得到的视图叫做主视图,从左面得到的视图叫做左视图,从上面得到的视图叫做俯视图.
知识拓展
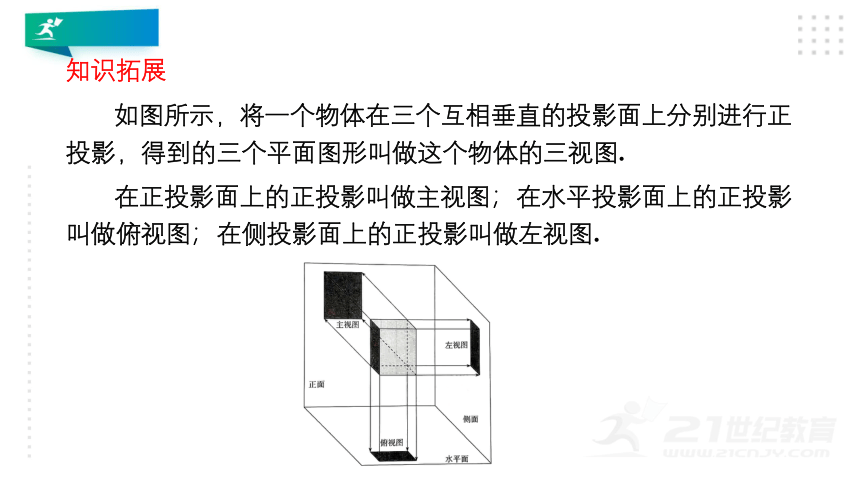
如图所示,将一个物体在三个互相垂直的投影面上分别进行正投影,得到的三个平面图形叫做这个物体的三视图.
在正投影面上的正投影叫做主视图;在水平投影面上的正投影叫做俯视图;在侧投影面上的正投影叫做左视图.
2.三视图的位置关系合
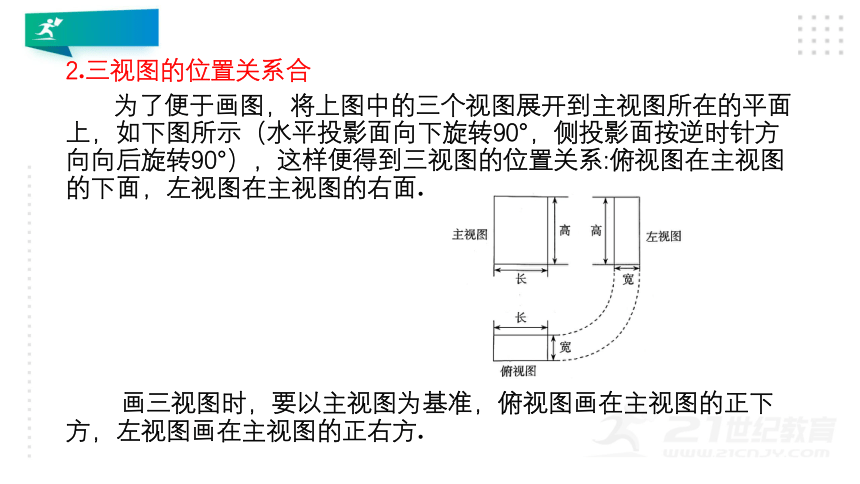
为了便于画图,将上图中的三个视图展开到主视图所在的平面上,如下图所示(水平投影面向下旋转90°,侧投影面按逆时针方向向后旋转90°),这样便得到三视图的位置关系:俯视图在主视图的下面,左视图在主视图的右面.
画三视图时,要以主视图为基准,俯视图画在主视图的正下方,左视图画在主视图的正右方.
3.画三视图的法则
一个几何体的三个视图分别从不同方向反映了一个几何体的形状和大小.主视图反映几何体的长与高,俯视图反映几何体的长与宽,左视图反映几何体的高与宽.因此,三视图能全面地反映几何体的形状和大小.
三视图的画法必须遵循以下法则:
主、俯两图长对正,主、左两图高平齐,左、俯两图宽相等.
简述为长对正,高平齐,宽相等.
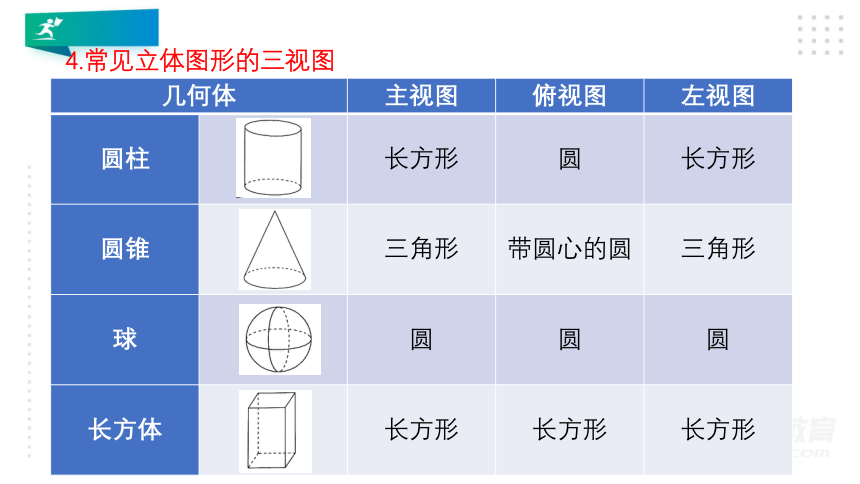
4.常见立体图形的三视图
几何体 主视图 俯视图 左视图
圆柱 长方形 圆 长方形
圆锥 三角形 带圆心的圆 三角形
球 圆 圆 圆
长方体 长方形 长方形 长方形
5.画三视图的步骤
(1)确定主视图的位置,画出主视图.
(2)根据“长对正”与几何体的宽画出俯视图.
(3)根据“高平齐”与“宽相等”画出左视图.
6.画三视图的注意事项
(1)三视图的外轮廓及内部结构都需遵循画三视图的法则;
(2)看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线;
(3)当虚线与实线重合时,画成实线;
(4)圆锥体顶端的视图为一个点.
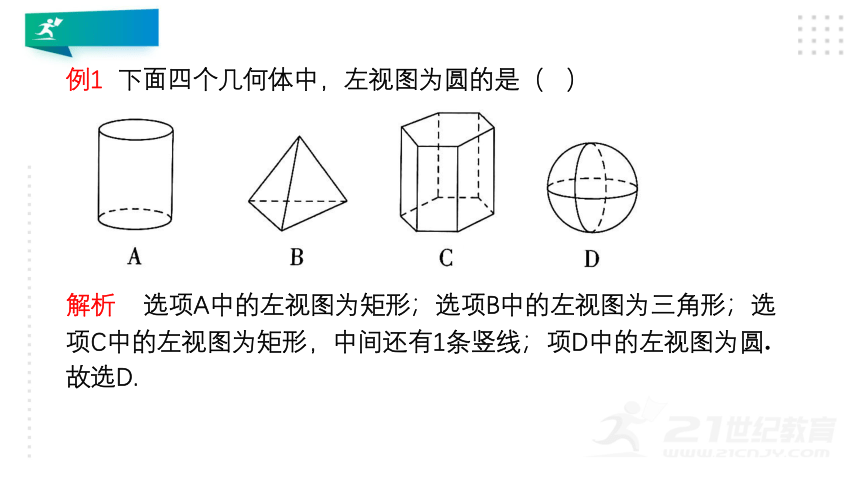
例1 下面四个几何体中,左视图为圆的是( )
例1 下面四个几何体中,左视图为圆的是( )
解析 选项A中的左视图为矩形;选项B中的左视图为三角形;选项C中的左视图为矩形,中间还有1条竖线;项D中的左视图为圆.故选D.
知识点二 简单组合体的三视图
日常生活中看到的很多物体,它们的形状不是很规则,但是它们一般可以看作是由一些基本几何体(棱柱、圆柱、圆锥、球等)组合成的或切割而成的.
画简单组合体的三视图的方法:
(1)认真观察,判断组合体由哪些基本几何体(几何体的一部分)组成,要注意分析基本几何体的摆放位置,如左右、前后、上下或内外关系.
(2)按照画几何体三视图的方法正确画出它的三视图.
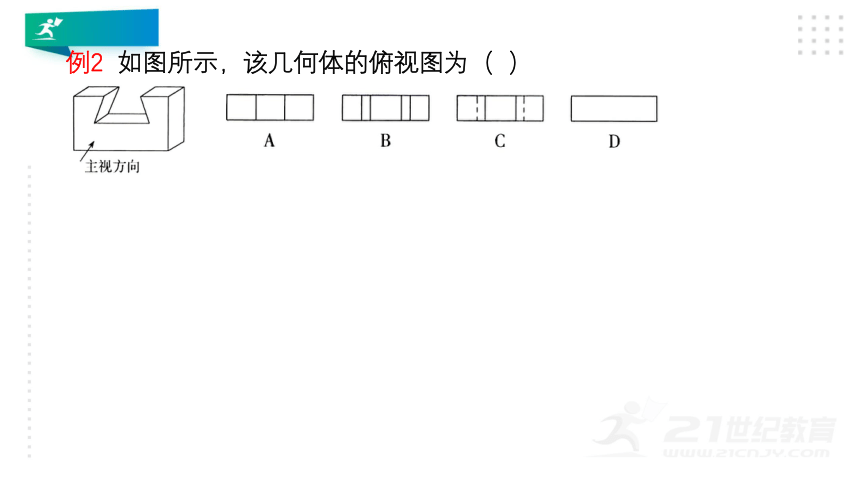
例2 如图所示,该几何体的俯视图为( )
例2 如图所示,该几何体的俯视图为( )
解析 该几何体的俯视图如图所示.
故选 C
例2 如图所示,该几何体的俯视图为( )
解析 该几何体的俯视图如图所示.
故选 C
归纳总结 判断基本立体图形组合体的三视图时,需明确各基本立体图形的三视图,再进行组合判断注意看得见的轮廓线画成实线,看不见的轮廓线画成虚线.
知识点三 由视图还原几何体
由三视图还原几何体是由二维平面图形判断三维立体图形,需具有空间观念.一般先由各视图想象从各个方向看到的几何体的形状,然后综合起来确定几何体的形状,再根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置以及各个面的尺寸.
例3 诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图所示,是对某物体从不同角度观察的记录情况,对该物体的判断最接近本质的是( )
A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管
B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管
C.是圆柱形物体,里面有两个垂直的空心管
D.是圆柱形物体,里面有两个平行的空心管
解析 由题图可得,该物体是圆柱形物体,里面有两个平行的空心管.故选D.
解析 由题图可得,该物体是圆柱形物体,里面有两个平行的空心管.故选D.
方法归纳 一般立体图形是几种基本立体图形的组合体或由基本立体图形切割而成在由三视图判断立体图形时,首先可根据三视图判断立体图形由哪些基本几何体组成或切割而成,再由轮廓线判断基本几何体的位置关系,如左右、前后、上下或内外关系.
经典例题
题型一 判断几何体的三视图
例1 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
题型一 判断几何体的三视图
例1 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
解析 它的左视图如图所示:
故选C.
题型一 判断几何体的三视图
例1 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
解析 它的左视图如图所示:
故选C.
特别提醒 判断三视图要注意,看不见的轮廓线要画成虚线.
题型二 有关三视图的计算
例2 一个几何体的三视图如图所示,则该几何体的表面积为_________.
题型二 有关三视图的计算
例2 一个几何体的三视图如图所示,则该几何体的表面积为_________.
解析 由题图可知该几何体为半圆柱,其底面直径为2,高为2,
故其表面积为π×12+2π÷2×2+2×2=3π+4.
题型二 有关三视图的计算
例2 一个几何体的三视图如图所示,则该几何体的表面积为_________.
解析 由题图可知该几何体为半圆柱,其底面直径为2,高为2,
故其表面积为π×12+2π÷2×2+2×2=3π+4.
归纳总结 解决此类题首先要具有将平面图形转化成立体图形的能力,其次是根据三视图的有关数据判断几何体的有关数据,并根据有关公式进行计算.
易错易混
易错点 忽略三视图的内部轮廓线
画三视图时要做到三对应,即“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”,这个三对应除了外部轮廓线要做到,内部轮廓线也应做到不少同学对此不清楚,画三视图时常出错.
例 如图所示,试画出该物体的三种视图.
例 如图所示,试画出该物体的三种视图.
解析 如图所示:
例 如图所示,试画出该物体的三种视图.
解析 如图所示:
易错警示 画三视图时,内部轮廓线也要做到“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”.
第四章 投影与视图
2 视图
知识点一 三视图及常见几何体的三视图
1.三视图的定义
在实际生活中,人们常常从正面、左面和上面三个不同的方向观察一个物体,分别得到这个物体的三种视图,这样大体上就把一个物体的形状特征用平面图形表示出来了.
通常我们把从正面得到的视图叫做主视图,从左面得到的视图叫做左视图,从上面得到的视图叫做俯视图.
知识拓展
如图所示,将一个物体在三个互相垂直的投影面上分别进行正投影,得到的三个平面图形叫做这个物体的三视图.
在正投影面上的正投影叫做主视图;在水平投影面上的正投影叫做俯视图;在侧投影面上的正投影叫做左视图.
2.三视图的位置关系合
为了便于画图,将上图中的三个视图展开到主视图所在的平面上,如下图所示(水平投影面向下旋转90°,侧投影面按逆时针方向向后旋转90°),这样便得到三视图的位置关系:俯视图在主视图的下面,左视图在主视图的右面.
画三视图时,要以主视图为基准,俯视图画在主视图的正下方,左视图画在主视图的正右方.
3.画三视图的法则
一个几何体的三个视图分别从不同方向反映了一个几何体的形状和大小.主视图反映几何体的长与高,俯视图反映几何体的长与宽,左视图反映几何体的高与宽.因此,三视图能全面地反映几何体的形状和大小.
三视图的画法必须遵循以下法则:
主、俯两图长对正,主、左两图高平齐,左、俯两图宽相等.
简述为长对正,高平齐,宽相等.
4.常见立体图形的三视图
几何体 主视图 俯视图 左视图
圆柱 长方形 圆 长方形
圆锥 三角形 带圆心的圆 三角形
球 圆 圆 圆
长方体 长方形 长方形 长方形
5.画三视图的步骤
(1)确定主视图的位置,画出主视图.
(2)根据“长对正”与几何体的宽画出俯视图.
(3)根据“高平齐”与“宽相等”画出左视图.
6.画三视图的注意事项
(1)三视图的外轮廓及内部结构都需遵循画三视图的法则;
(2)看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线;
(3)当虚线与实线重合时,画成实线;
(4)圆锥体顶端的视图为一个点.
例1 下面四个几何体中,左视图为圆的是( )
例1 下面四个几何体中,左视图为圆的是( )
解析 选项A中的左视图为矩形;选项B中的左视图为三角形;选项C中的左视图为矩形,中间还有1条竖线;项D中的左视图为圆.故选D.
知识点二 简单组合体的三视图
日常生活中看到的很多物体,它们的形状不是很规则,但是它们一般可以看作是由一些基本几何体(棱柱、圆柱、圆锥、球等)组合成的或切割而成的.
画简单组合体的三视图的方法:
(1)认真观察,判断组合体由哪些基本几何体(几何体的一部分)组成,要注意分析基本几何体的摆放位置,如左右、前后、上下或内外关系.
(2)按照画几何体三视图的方法正确画出它的三视图.
例2 如图所示,该几何体的俯视图为( )
例2 如图所示,该几何体的俯视图为( )
解析 该几何体的俯视图如图所示.
故选 C
例2 如图所示,该几何体的俯视图为( )
解析 该几何体的俯视图如图所示.
故选 C
归纳总结 判断基本立体图形组合体的三视图时,需明确各基本立体图形的三视图,再进行组合判断注意看得见的轮廓线画成实线,看不见的轮廓线画成虚线.
知识点三 由视图还原几何体
由三视图还原几何体是由二维平面图形判断三维立体图形,需具有空间观念.一般先由各视图想象从各个方向看到的几何体的形状,然后综合起来确定几何体的形状,再根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置以及各个面的尺寸.
例3 诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图所示,是对某物体从不同角度观察的记录情况,对该物体的判断最接近本质的是( )
A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管
B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管
C.是圆柱形物体,里面有两个垂直的空心管
D.是圆柱形物体,里面有两个平行的空心管
解析 由题图可得,该物体是圆柱形物体,里面有两个平行的空心管.故选D.
解析 由题图可得,该物体是圆柱形物体,里面有两个平行的空心管.故选D.
方法归纳 一般立体图形是几种基本立体图形的组合体或由基本立体图形切割而成在由三视图判断立体图形时,首先可根据三视图判断立体图形由哪些基本几何体组成或切割而成,再由轮廓线判断基本几何体的位置关系,如左右、前后、上下或内外关系.
经典例题
题型一 判断几何体的三视图
例1 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
题型一 判断几何体的三视图
例1 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
解析 它的左视图如图所示:
故选C.
题型一 判断几何体的三视图
例1 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
解析 它的左视图如图所示:
故选C.
特别提醒 判断三视图要注意,看不见的轮廓线要画成虚线.
题型二 有关三视图的计算
例2 一个几何体的三视图如图所示,则该几何体的表面积为_________.
题型二 有关三视图的计算
例2 一个几何体的三视图如图所示,则该几何体的表面积为_________.
解析 由题图可知该几何体为半圆柱,其底面直径为2,高为2,
故其表面积为π×12+2π÷2×2+2×2=3π+4.
题型二 有关三视图的计算
例2 一个几何体的三视图如图所示,则该几何体的表面积为_________.
解析 由题图可知该几何体为半圆柱,其底面直径为2,高为2,
故其表面积为π×12+2π÷2×2+2×2=3π+4.
归纳总结 解决此类题首先要具有将平面图形转化成立体图形的能力,其次是根据三视图的有关数据判断几何体的有关数据,并根据有关公式进行计算.
易错易混
易错点 忽略三视图的内部轮廓线
画三视图时要做到三对应,即“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”,这个三对应除了外部轮廓线要做到,内部轮廓线也应做到不少同学对此不清楚,画三视图时常出错.
例 如图所示,试画出该物体的三种视图.
例 如图所示,试画出该物体的三种视图.
解析 如图所示:
例 如图所示,试画出该物体的三种视图.
解析 如图所示:
易错警示 画三视图时,内部轮廓线也要做到“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”.
