3.2代数式 同步达标测评 2021-2022学年鲁教版(五四制)六年级数学上册(word版含答案)
文档属性
| 名称 | 3.2代数式 同步达标测评 2021-2022学年鲁教版(五四制)六年级数学上册(word版含答案) | 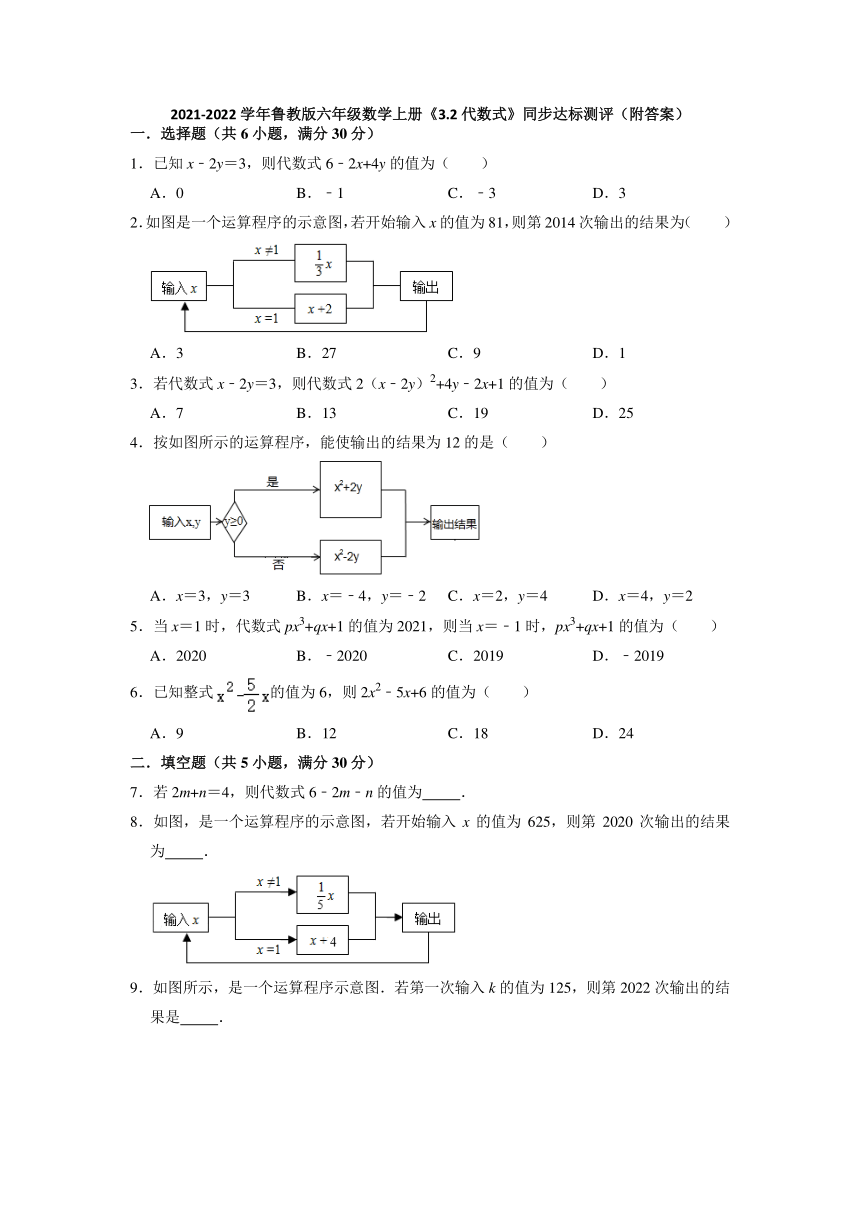 | |
| 格式 | doc | ||
| 文件大小 | 120.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 14:02:14 | ||
图片预览




文档简介
2021-2022学年鲁教版六年级数学上册《3.2代数式》同步达标测评(附答案)
一.选择题(共6小题,满分30分)
1.已知x﹣2y=3,则代数式6﹣2x+4y的值为( )
A.0 B.﹣1 C.﹣3 D.3
2.如图是一个运算程序的示意图,若开始输入x的值为81,则第2014次输出的结果为( )
A.3 B.27 C.9 D.1
3.若代数式x﹣2y=3,则代数式2(x﹣2y)2+4y﹣2x+1的值为( )
A.7 B.13 C.19 D.25
4.按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x=﹣4,y=﹣2 C.x=2,y=4 D.x=4,y=2
5.当x=1时,代数式px3+qx+1的值为2021,则当x=﹣1时,px3+qx+1的值为( )
A.2020 B.﹣2020 C.2019 D.﹣2019
6.已知整式的值为6,则2x2﹣5x+6的值为( )
A.9 B.12 C.18 D.24
二.填空题(共5小题,满分30分)
7.若2m+n=4,则代数式6﹣2m﹣n的值为 .
8.如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为 .
9.如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2022次输出的结果是 .
10.已知y=3xy+x,求代数式= .
11.已知x+2y=7,4m﹣3n=8,则代数式(9n﹣4y)﹣2(6m+x)+3的值为 .
三.解答题(共7小题,满分60分)
12.如图,大小两个正方形的边长分别为a、b.
(1)用含a、b的代数式表示阴影部分的面积S;
(2)如果a=6,b=4,求阴影部分的面积.
13.先阅读下面例题的解题过程,再解决后面的题目.
例:已知9﹣6y﹣4y2=7,求2y2+3y+7的值.
解:由9﹣6y﹣4y2=7,得﹣6y﹣4y2=7﹣9,即6y+4y2=2,所以2y2+3y=1,所以2y2+3y+7=8.
题目:已知代数式14x+5﹣21x2的值是﹣2,求6x2﹣4x+5的值.
14.如图,小明家的住房结构平面图,(单位:米),装修房子时,他打算将卧室以外的部分都铺上地砖.
(1)若铺地砖的价格为80元/平方米,那么购买地砖需要花多少钱?(用代数式表示);
(2)已知房屋的高度为3米,现在想要在客厅和卧室的墙壁上贴上壁纸,那么需要多少平方米的壁纸(门窗所占面积忽略不计)?(用代数式表示);
(3)若x=4,y=5,且每平方米地砖的价格是90元,每平方米壁纸的价格是15元,那么,在这两项装修中,小明共要花费多少钱?(各种小的损耗不计).
15.若a、b互为相反数,c、d互为倒数,x的绝对值为2,且x<0,求的值.
16.如图所示是一个长方形.
(1)根据图中尺寸大小,用含x的代数式表示阴影部分的面积S;
(2)若x=3,求S的值.
17.电动车厂计划每天平均生产n辆电动车(每周工作五天),而实际产量与计划产量相比有出入,下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
日期 星期一 星期二 星期三 星期四 星期五
实际生产量 +5 ﹣1 ﹣6 +13 ﹣2
(1)用含n的整式表示本周五天生产电动车的总数;
(2)该厂实行每日计件工资制,每生产一辆车可得200元,若超额完成任务,则超过部分每辆另奖55元;少生产一辆扣60元,当n=50时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=50时,在此方式下这一周工人的工资总额与按日计件的工资哪一个更多?请说明理由.
18.一个三位数,三个数位上的数字(以百位、十位、个位为顺序)排列了三个连续整数(由大到小排列),设十位上的数字为n.
(1)用关于n的式子表示这个三位数;
(2)这个三位数一定能被3整除吗?请说明理由.
参考答案
一.选择题(共6小题,满分30分)
1.解:∵x﹣2y=3,
∴6﹣2x+4y=6﹣2(x﹣2y)=6﹣2×3=6﹣6=0
故选:A.
2.解:第1次,×81=27,
第2次,×27=9,
第3次,×9=3,
第4次,×3=1,
第5次,1+2=3,
第6次,×3=1,
…,
依此类推,偶数次运算输出的结果是1,奇数次运算输出的结果是3,
∵2014是偶数,
∴第2014次输出的结果为1.
故选:D.
3.解:∵x﹣2y=3,
∴2(x﹣2y)2+4y﹣2x+1
=2(x﹣2y)2﹣2(x﹣2y)+1
=2×32﹣2×3+1
=18﹣6+1
=13.
故选:B.
4.解:A、x=3、y=3时,输出结果为32+2×3=15,不符合题意;
B、x=﹣4、y=﹣2时,输出结果为(﹣4)2﹣2×(﹣2)=20,不符合题意;
C、x=2、y=4时,输出结果为22+2×4=12,符合题意;
D、x=4、y=2时,输出结果为42+2×2=20,不符合题意;
故选:C.
5.解:将x=1代入px3+qx+1=2021可得p+q=2020,
当x=﹣1时,
px3+qx+1
=﹣p﹣q+1
=﹣(p+q)+1
=﹣2020+1
=﹣2019,
故选:D.
6.解:∵=6
∴2x2﹣5x+6=2()+6
=2×6+6=18,故选:C.
二.填空题(共5小题,满分30分)
7.解:∵2m+n=4,
∴6﹣2m﹣n=6﹣(2m+n)=6﹣4=2,
故答案为2.
8.解:当x=625时,x=125,
当x=125时,x=25,
当x=25时,x=5,
当x=5时,x=1,
当x=1时,x+4=5,
当x=5时,x=1,
…
依此类推,以5,1循环,
(2020﹣2)÷2=1009,能够整除,
所以输出的结果是1,
故答案为:1
9.解:∵第1次输出的结果是25,第2次输出的结果是5,第3次输出的结果是1,第4次输出的结果是5,第5次输出的结果是1,…,
∴第2n次输出的结果是5,第2n+1次输出的结果是1(n为正整数),
∴第2022次输出的结果是5.
故答案为:5.
10.解:∵y=3xy+x,
∴x﹣y=﹣3xy,
∴
=
=
=
=.
故答案为:.
11.解:(9n﹣4y)﹣2(6m+x)+3
=9n﹣4y﹣12m﹣2x+3
=﹣3(4m﹣3n)﹣2(x+2y)+3,
将x+2y=7,4m﹣3n=8代入,
﹣3(4m﹣3n)﹣2(x+2y)+3
=﹣24﹣14+3
=﹣35.
三.解答题(共7小题,满分60分)
12.解:(1)大小两个正方形的边长分别为a、b,
∴阴影部分的面积为:
S=a2+b2﹣a2﹣(a+b)b
=a2+b2﹣ab;
(2)∵a=6,b=4,
∴S=a2+b2﹣ab
=×62+×42﹣×6×4
=18+8﹣12
=14.
所以阴影部分的面积是14.
13.解:∵14x+5﹣21x2的值是﹣2,
∴14x﹣21x2=﹣7,
即2x﹣3x2=﹣1,
∴3x2﹣2x=1,
则6x2﹣4x+5=2×(3x2﹣2x)+5=7.
14.解:(1)卫生间面积=y(4x﹣x﹣2x)=xy,
厨房面积=x(4y﹣2y)=2xy,
客厅面积=2x 4y=8xy,
∴铺地砖的面积=xy+2xy+8xy=11xy,
∴铺地砖的花费为880xy元;
(2)卧室的壁纸=(2y+2y+2x+2x)×3=(12x+12y)平方米,
客厅的壁纸=2(2x+4y)×3=(12x+24y)平方米,
∴共需要壁纸为12x+12y+12x+24y=(24x+36y)平方米;
(3)当x=4,y=5时,
地砖需要花费:90×11×4×5=19800(元),
壁纸需要花费:(24×4+36×5)×15=4140(元),
∴小明共花费19800+4140=23940(元).
15.解:∵a、b互为相反数,c、d互为倒数,x的绝对值为2,且x<0,
∴a+b=0,cd=1,x=﹣2.
∴原式=﹣2﹣(0+1)+=﹣2﹣1=﹣3.
16.解:(1)由图形可知:S=4×8﹣×4×8﹣×4(4﹣x)
=16﹣8+2x
=8+2x.
另解:大三角形面积为:×4×8=16,
小直角三角形的面积为:×(8﹣4)×(4﹣x)=8﹣2x,
∴S=16﹣(8﹣2x)=8+2x.
(2)将x=3代入上式,S=8+2×3=14
17.解:(1)n+5+n﹣1+n﹣6+n+13+n﹣2=5n+9;
(2)当n=50时,5n+9=5×50+9=259,
200×259+55(5+13)+60(﹣1﹣6﹣2)=52250,
所以该厂工人这一周的工资总额是52250元.
(3)5+(﹣1)+(﹣6)+13+(﹣2)=9,
259×200+9×55=52295,
∵52250<52295,
∴每周计件工资制一周工人的工资总额更多.
18.解:(1)设十位上的数字为n,则百位上的数是n+1,个位上的数是n﹣1,
则这个三位数是100(n+1)+10n+(n﹣1)=111n+99.
(2)根据题意得:111n+99=3(37n+33),
则这个三位数一定能被3整除.
一.选择题(共6小题,满分30分)
1.已知x﹣2y=3,则代数式6﹣2x+4y的值为( )
A.0 B.﹣1 C.﹣3 D.3
2.如图是一个运算程序的示意图,若开始输入x的值为81,则第2014次输出的结果为( )
A.3 B.27 C.9 D.1
3.若代数式x﹣2y=3,则代数式2(x﹣2y)2+4y﹣2x+1的值为( )
A.7 B.13 C.19 D.25
4.按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x=﹣4,y=﹣2 C.x=2,y=4 D.x=4,y=2
5.当x=1时,代数式px3+qx+1的值为2021,则当x=﹣1时,px3+qx+1的值为( )
A.2020 B.﹣2020 C.2019 D.﹣2019
6.已知整式的值为6,则2x2﹣5x+6的值为( )
A.9 B.12 C.18 D.24
二.填空题(共5小题,满分30分)
7.若2m+n=4,则代数式6﹣2m﹣n的值为 .
8.如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为 .
9.如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2022次输出的结果是 .
10.已知y=3xy+x,求代数式= .
11.已知x+2y=7,4m﹣3n=8,则代数式(9n﹣4y)﹣2(6m+x)+3的值为 .
三.解答题(共7小题,满分60分)
12.如图,大小两个正方形的边长分别为a、b.
(1)用含a、b的代数式表示阴影部分的面积S;
(2)如果a=6,b=4,求阴影部分的面积.
13.先阅读下面例题的解题过程,再解决后面的题目.
例:已知9﹣6y﹣4y2=7,求2y2+3y+7的值.
解:由9﹣6y﹣4y2=7,得﹣6y﹣4y2=7﹣9,即6y+4y2=2,所以2y2+3y=1,所以2y2+3y+7=8.
题目:已知代数式14x+5﹣21x2的值是﹣2,求6x2﹣4x+5的值.
14.如图,小明家的住房结构平面图,(单位:米),装修房子时,他打算将卧室以外的部分都铺上地砖.
(1)若铺地砖的价格为80元/平方米,那么购买地砖需要花多少钱?(用代数式表示);
(2)已知房屋的高度为3米,现在想要在客厅和卧室的墙壁上贴上壁纸,那么需要多少平方米的壁纸(门窗所占面积忽略不计)?(用代数式表示);
(3)若x=4,y=5,且每平方米地砖的价格是90元,每平方米壁纸的价格是15元,那么,在这两项装修中,小明共要花费多少钱?(各种小的损耗不计).
15.若a、b互为相反数,c、d互为倒数,x的绝对值为2,且x<0,求的值.
16.如图所示是一个长方形.
(1)根据图中尺寸大小,用含x的代数式表示阴影部分的面积S;
(2)若x=3,求S的值.
17.电动车厂计划每天平均生产n辆电动车(每周工作五天),而实际产量与计划产量相比有出入,下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
日期 星期一 星期二 星期三 星期四 星期五
实际生产量 +5 ﹣1 ﹣6 +13 ﹣2
(1)用含n的整式表示本周五天生产电动车的总数;
(2)该厂实行每日计件工资制,每生产一辆车可得200元,若超额完成任务,则超过部分每辆另奖55元;少生产一辆扣60元,当n=50时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=50时,在此方式下这一周工人的工资总额与按日计件的工资哪一个更多?请说明理由.
18.一个三位数,三个数位上的数字(以百位、十位、个位为顺序)排列了三个连续整数(由大到小排列),设十位上的数字为n.
(1)用关于n的式子表示这个三位数;
(2)这个三位数一定能被3整除吗?请说明理由.
参考答案
一.选择题(共6小题,满分30分)
1.解:∵x﹣2y=3,
∴6﹣2x+4y=6﹣2(x﹣2y)=6﹣2×3=6﹣6=0
故选:A.
2.解:第1次,×81=27,
第2次,×27=9,
第3次,×9=3,
第4次,×3=1,
第5次,1+2=3,
第6次,×3=1,
…,
依此类推,偶数次运算输出的结果是1,奇数次运算输出的结果是3,
∵2014是偶数,
∴第2014次输出的结果为1.
故选:D.
3.解:∵x﹣2y=3,
∴2(x﹣2y)2+4y﹣2x+1
=2(x﹣2y)2﹣2(x﹣2y)+1
=2×32﹣2×3+1
=18﹣6+1
=13.
故选:B.
4.解:A、x=3、y=3时,输出结果为32+2×3=15,不符合题意;
B、x=﹣4、y=﹣2时,输出结果为(﹣4)2﹣2×(﹣2)=20,不符合题意;
C、x=2、y=4时,输出结果为22+2×4=12,符合题意;
D、x=4、y=2时,输出结果为42+2×2=20,不符合题意;
故选:C.
5.解:将x=1代入px3+qx+1=2021可得p+q=2020,
当x=﹣1时,
px3+qx+1
=﹣p﹣q+1
=﹣(p+q)+1
=﹣2020+1
=﹣2019,
故选:D.
6.解:∵=6
∴2x2﹣5x+6=2()+6
=2×6+6=18,故选:C.
二.填空题(共5小题,满分30分)
7.解:∵2m+n=4,
∴6﹣2m﹣n=6﹣(2m+n)=6﹣4=2,
故答案为2.
8.解:当x=625时,x=125,
当x=125时,x=25,
当x=25时,x=5,
当x=5时,x=1,
当x=1时,x+4=5,
当x=5时,x=1,
…
依此类推,以5,1循环,
(2020﹣2)÷2=1009,能够整除,
所以输出的结果是1,
故答案为:1
9.解:∵第1次输出的结果是25,第2次输出的结果是5,第3次输出的结果是1,第4次输出的结果是5,第5次输出的结果是1,…,
∴第2n次输出的结果是5,第2n+1次输出的结果是1(n为正整数),
∴第2022次输出的结果是5.
故答案为:5.
10.解:∵y=3xy+x,
∴x﹣y=﹣3xy,
∴
=
=
=
=.
故答案为:.
11.解:(9n﹣4y)﹣2(6m+x)+3
=9n﹣4y﹣12m﹣2x+3
=﹣3(4m﹣3n)﹣2(x+2y)+3,
将x+2y=7,4m﹣3n=8代入,
﹣3(4m﹣3n)﹣2(x+2y)+3
=﹣24﹣14+3
=﹣35.
三.解答题(共7小题,满分60分)
12.解:(1)大小两个正方形的边长分别为a、b,
∴阴影部分的面积为:
S=a2+b2﹣a2﹣(a+b)b
=a2+b2﹣ab;
(2)∵a=6,b=4,
∴S=a2+b2﹣ab
=×62+×42﹣×6×4
=18+8﹣12
=14.
所以阴影部分的面积是14.
13.解:∵14x+5﹣21x2的值是﹣2,
∴14x﹣21x2=﹣7,
即2x﹣3x2=﹣1,
∴3x2﹣2x=1,
则6x2﹣4x+5=2×(3x2﹣2x)+5=7.
14.解:(1)卫生间面积=y(4x﹣x﹣2x)=xy,
厨房面积=x(4y﹣2y)=2xy,
客厅面积=2x 4y=8xy,
∴铺地砖的面积=xy+2xy+8xy=11xy,
∴铺地砖的花费为880xy元;
(2)卧室的壁纸=(2y+2y+2x+2x)×3=(12x+12y)平方米,
客厅的壁纸=2(2x+4y)×3=(12x+24y)平方米,
∴共需要壁纸为12x+12y+12x+24y=(24x+36y)平方米;
(3)当x=4,y=5时,
地砖需要花费:90×11×4×5=19800(元),
壁纸需要花费:(24×4+36×5)×15=4140(元),
∴小明共花费19800+4140=23940(元).
15.解:∵a、b互为相反数,c、d互为倒数,x的绝对值为2,且x<0,
∴a+b=0,cd=1,x=﹣2.
∴原式=﹣2﹣(0+1)+=﹣2﹣1=﹣3.
16.解:(1)由图形可知:S=4×8﹣×4×8﹣×4(4﹣x)
=16﹣8+2x
=8+2x.
另解:大三角形面积为:×4×8=16,
小直角三角形的面积为:×(8﹣4)×(4﹣x)=8﹣2x,
∴S=16﹣(8﹣2x)=8+2x.
(2)将x=3代入上式,S=8+2×3=14
17.解:(1)n+5+n﹣1+n﹣6+n+13+n﹣2=5n+9;
(2)当n=50时,5n+9=5×50+9=259,
200×259+55(5+13)+60(﹣1﹣6﹣2)=52250,
所以该厂工人这一周的工资总额是52250元.
(3)5+(﹣1)+(﹣6)+13+(﹣2)=9,
259×200+9×55=52295,
∵52250<52295,
∴每周计件工资制一周工人的工资总额更多.
18.解:(1)设十位上的数字为n,则百位上的数是n+1,个位上的数是n﹣1,
则这个三位数是100(n+1)+10n+(n﹣1)=111n+99.
(2)根据题意得:111n+99=3(37n+33),
则这个三位数一定能被3整除.
