2021-2022学年人教版八年级上册数学13.3.1等腰三角形课件(18张)
文档属性
| 名称 | 2021-2022学年人教版八年级上册数学13.3.1等腰三角形课件(18张) |
|
|
| 格式 | zip | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 12:10:17 | ||
图片预览





文档简介
(共18张PPT)
情境导入
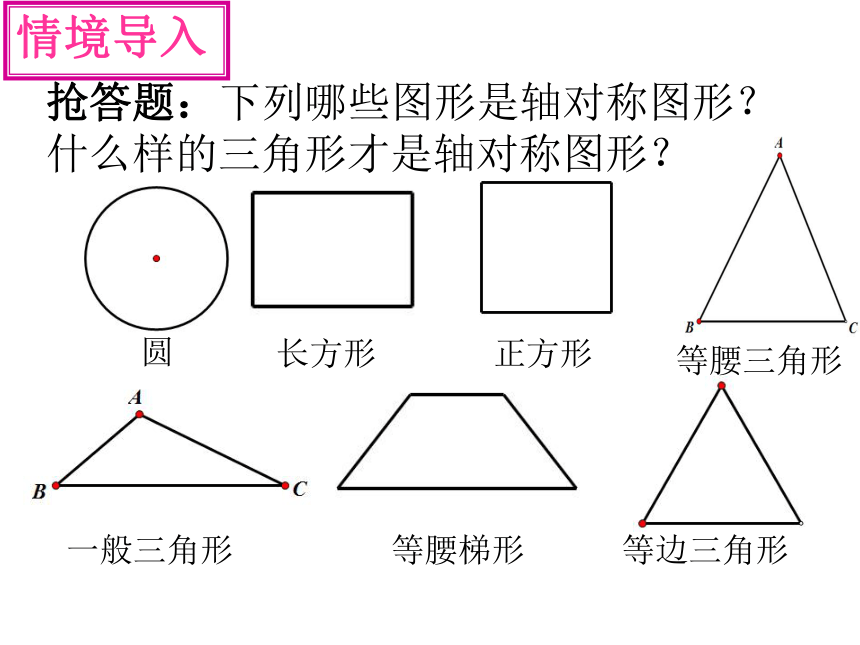
抢答题:下列哪些图形是轴对称图形?什么样的三角形才是轴对称图形?
圆
长方形
正方形
等腰三角形
一般三角形
等腰梯形
等边三角形
13.3.1等腰三角形(2课时)
第1课时 等腰三角形的性质和应用
1、理解并掌握等腰三角形的性质。
2、运用等腰三角形的性质进行证明和计算
探究
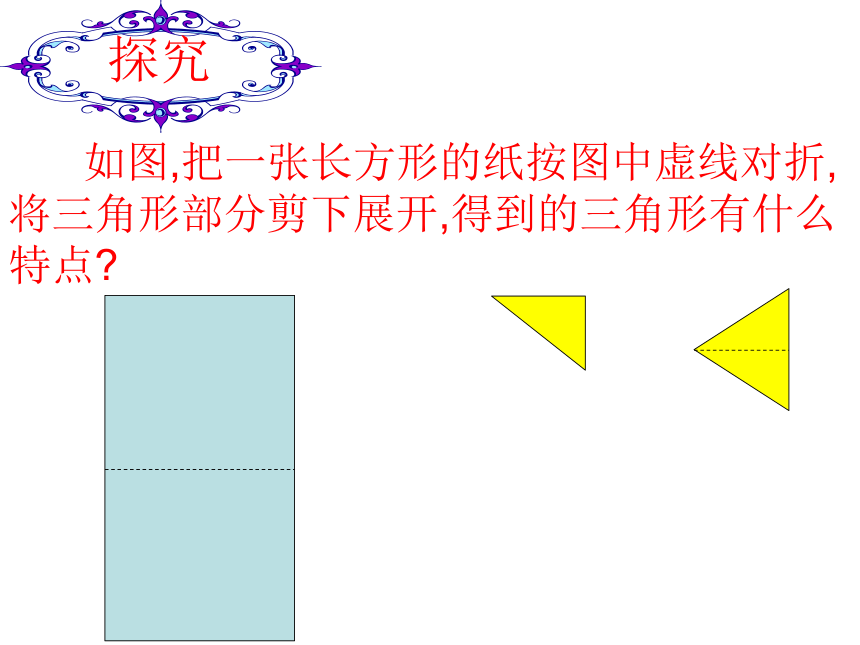
如图,把一张长方形的纸按图中虚线对折,将三角形部分剪下展开,得到的三角形有什么特点
腰—相等的两边
底—除腰外的一边
顶角—两腰的夹角
底角—腰与底的夹角
有两边相等的三角形叫做等腰三角形。
概念:
( △ABC ,AB=AC )
想一想
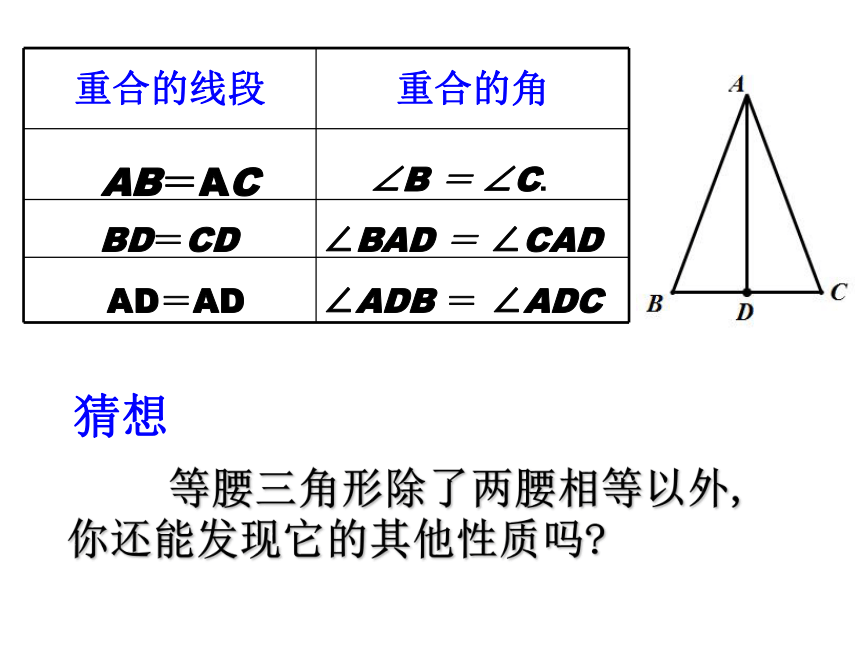
1、把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角。
2、由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想。
重合的线段 重合的角
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗
猜想
等腰三角形的性质1
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD (SAS)
∴ ∠B=∠C (全等三角形对应角相等)
方法一
你还有其他方法吗?
第二种
第三种
A
B
C
D
A
B
C
D
┌
作△ABC的高线AD,垂直底边BC于D。
作△ABC的中线AD,交底边BC于D。
性质1:
等腰三角形的两个底角相等(简写为“等边对等角”)
性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合。
(简写为“三线合一”)
我们可以发现等腰三角形的性质:
∵ △ABC,AB=AC
∴∠B=∠C
等腰三角形的两个底角相等三种表示形式
等腰三角形的
两个底角相等。
2、文字语言
3、符号语言
1、图形语言
例:如图在△ABC中,AB=AC,点D在AC上,且BD=BC=AD求△ABC各角的度数.
例题解析
解:∵AB=AC, BD=BC=AD
∴∠ABC=∠1=∠2
∠3=∠4
设∠3=x,
则∠2=∠3+∠4=2x
从而∠ABC=∠1=∠2=2x
在△ABC中,有
∠A+∠ABC+∠C=∠3+∠ABC+∠1
=x+2x+2x=180
解得x=36
在△ABC中,∠A=36°,
∠ABC=∠C=72°
练一练
1、如图,在下列等腰三角形中,分别求出它们的底角和顶角的度数
2、如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF
(提示利用等腰三角形三线合一性质及角平分线性质解题)
证明:∵D为BC的中点,AB=AC,
∴AD平分∠BAC(三线合一)
又∵DE⊥AB,DF⊥AC
∴DE=DF(角平分线的性质)
课堂小结
通过这节课的学习,同学们有什么收获?
1、必做题:
课本77页练习第2、3题
2、选做题:
课本83页第14题
课后作业
情境导入
抢答题:下列哪些图形是轴对称图形?什么样的三角形才是轴对称图形?
圆
长方形
正方形
等腰三角形
一般三角形
等腰梯形
等边三角形
13.3.1等腰三角形(2课时)
第1课时 等腰三角形的性质和应用
1、理解并掌握等腰三角形的性质。
2、运用等腰三角形的性质进行证明和计算
探究
如图,把一张长方形的纸按图中虚线对折,将三角形部分剪下展开,得到的三角形有什么特点
腰—相等的两边
底—除腰外的一边
顶角—两腰的夹角
底角—腰与底的夹角
有两边相等的三角形叫做等腰三角形。
概念:
( △ABC ,AB=AC )
想一想
1、把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角。
2、由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想。
重合的线段 重合的角
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗
猜想
等腰三角形的性质1
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD (SAS)
∴ ∠B=∠C (全等三角形对应角相等)
方法一
你还有其他方法吗?
第二种
第三种
A
B
C
D
A
B
C
D
┌
作△ABC的高线AD,垂直底边BC于D。
作△ABC的中线AD,交底边BC于D。
性质1:
等腰三角形的两个底角相等(简写为“等边对等角”)
性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合。
(简写为“三线合一”)
我们可以发现等腰三角形的性质:
∵ △ABC,AB=AC
∴∠B=∠C
等腰三角形的两个底角相等三种表示形式
等腰三角形的
两个底角相等。
2、文字语言
3、符号语言
1、图形语言
例:如图在△ABC中,AB=AC,点D在AC上,且BD=BC=AD求△ABC各角的度数.
例题解析
解:∵AB=AC, BD=BC=AD
∴∠ABC=∠1=∠2
∠3=∠4
设∠3=x,
则∠2=∠3+∠4=2x
从而∠ABC=∠1=∠2=2x
在△ABC中,有
∠A+∠ABC+∠C=∠3+∠ABC+∠1
=x+2x+2x=180
解得x=36
在△ABC中,∠A=36°,
∠ABC=∠C=72°
练一练
1、如图,在下列等腰三角形中,分别求出它们的底角和顶角的度数
2、如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF
(提示利用等腰三角形三线合一性质及角平分线性质解题)
证明:∵D为BC的中点,AB=AC,
∴AD平分∠BAC(三线合一)
又∵DE⊥AB,DF⊥AC
∴DE=DF(角平分线的性质)
课堂小结
通过这节课的学习,同学们有什么收获?
1、必做题:
课本77页练习第2、3题
2、选做题:
课本83页第14题
课后作业
