3.7探索与表达规律 解答题专题训练 2021-2022学年鲁教版(五四制)六年级数学上册(Word版含答案)
文档属性
| 名称 | 3.7探索与表达规律 解答题专题训练 2021-2022学年鲁教版(五四制)六年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 335.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 23:44:37 | ||
图片预览




文档简介
2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》解答题专题训练(附答案)
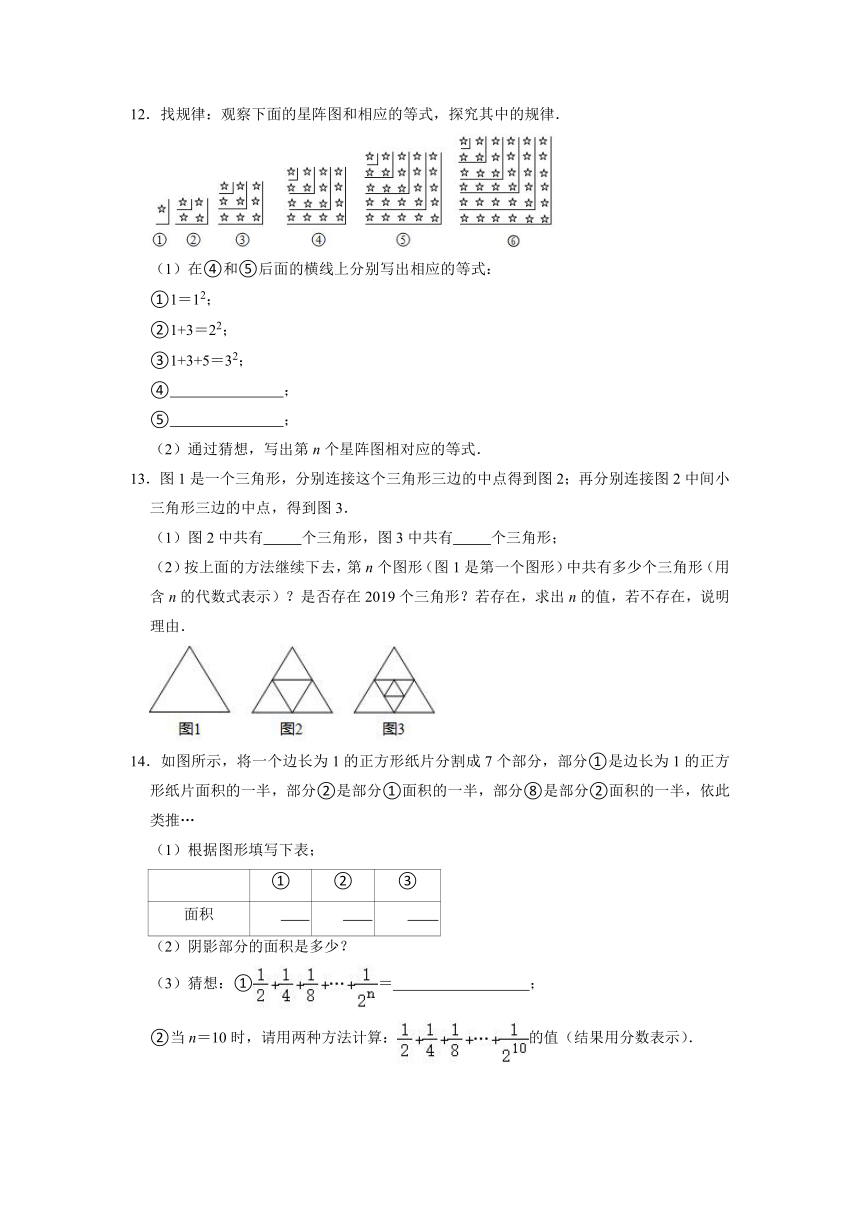
1.把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形…按此规律排列下去,解答下列问题:
(1)填写下列表格:
图序 ① ② ③ ④ …
黑色三角形个数 1 3 6 …
(2)若第 个图案中黑色三角形的个数有91个,求n的值.
2.观察下列图形与等式:
(1)观察图形,写出第(7)个等式: ;根据图中规律,写出第n个图形的规律: ;(用含有n的式子表示)
(2)求出10+11+…+80的值.
3.如图,是一组完全相同的黑白小球组成的图形:
观察上面各图及对应的关系式,根据发现的规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示,并证明其正确性).
4.用火柴棒按图中的方式搭图形:
按图示规律填空:
图形标号 ① ② ③ ④ ⑤
火柴棒根数 5 9 13 a b
(1)a= ,b= ;
(2)按照这种方式搭下去,则搭第n个图形需要火柴棒的根数为 ;(用含n的代数式来表示)
(3)按照这种方式搭下去,用(2)中的代数式求第2021个图形需要的火柴棒根数.
5.将围棋的白色棋子按如图所示的方式排列,图中的白色棋子被折线隔开分成若干层,第一层有1个白色棋子,第二层有3个白色棋子,第三层有5个白色棋子,第四层有7个白色棋子,…,以此类推,请观察图形规律,解答下列问题:
(1)第n层有 个白色棋子,图中从第一层到第n层一共有 个白色棋子;
(2)利用发现的规律计算:1921+1923+1925+…+2021的和.
6.如图1,给定一个正方形,要通过裁剪将其分割成若干个互不重叠的正方形.第1次裁剪分割成4个互不重叠的正方形,得到图2,称之为1个基本操作;第2次裁剪分割成7个互不重叠的正方形,得到图3,称之为2个基本操作…以后每次只在上次得到图形的左上角的正方形中裁剪.
(1)5个基本操作后,共裁剪成 个正方形;100个基本操作后,共裁剪成 个正方形;
(2)经过若干次基本操作后,能否得到2021个互不重叠的正方形?若能,求出是几个基本操作后得到的;若不能,请说明理由.
7.观察下列图形与等式的关系:
按照以上图形与等式的规律,解答下列问题:
(1)写出第5个等式: .
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明(已知:1+2+3+…+n=).
8.按如下规律摆放五角星:
(1)填写表格:
图案序号 1 2 3 4 … n
五角星个数 4 7 …
(2)直接写出第20个图案的五角星个数,个数为 ;
(3)若按上面的规律继续摆放,是否存在某个图案,其中恰好含有2021个五角星?
(4)计算前20个五角星图案中五角星的总个数.
9.按如下规律摆放三角形:
(1)图④中分别有 个三角形?
(2)按上述规律排列下去,第n个图形中有 个三角形?
(3)按上述规律排列下去,第2021个图形中有 个三角形?
10.如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有n(n>1)个点,每个图形的总点数记为S.
(Ⅰ)当n=4时,S的值为 ;当n=6时,S的值为 ;
(Ⅱ)每条“边”有n个点时的总点数S是 (用含n的式子表示);
(Ⅲ)当n=2021时,总点数S是多少?
11.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待73位顾客且要“同桌”就餐,但餐厅只有18张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
12.找规律:观察下面的星阵图和相应的等式,探究其中的规律.
(1)在④和⑤后面的横线上分别写出相应的等式:
①1=12;
②1+3=22;
③1+3+5=32;
④ ;
⑤ ;
(2)通过猜想,写出第n个星阵图相对应的等式.
13.图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形三边的中点,得到图3.
(1)图2中共有 个三角形,图3中共有 个三角形;
(2)按上面的方法继续下去,第n个图形(图1是第一个图形)中共有多少个三角形(用含n的代数式表示)?是否存在2019个三角形?若存在,求出n的值,若不存在,说明理由.
14.如图所示,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分⑧是部分②面积的一半,依此类推…
(1)根据图形填写下表;
① ② ③
面积
(2)阴影部分的面积是多少?
(3)猜想:①= ;
②当n=10时,请用两种方法计算:的值(结果用分数表示).
15.如图所示的是用棋子摆成的“T”字形图案.
(1)填写表:
图案序号 ① ② ③ ④ … ⑩
每个图案中棋子的个数 5 8 …
(2)第n个“T”字形图案中棋子的个数为 .(用含n的代数式表示)
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数为 .
16.观察下列各等式,并回答问题:
,,,,….
(1)填空:= ;= (n为整数);
(2)计算:;
(3)计算:.
17.观察下面的等式:
第1个等式:=×(1﹣);
第2个等式:=×(﹣);
第3个等式:=×(﹣);
第4个等式:=×(﹣);
…
解答下面的问题:
(1)+++…+= ;
(2)若n为正整数,请你猜想= ,并证明你猜想的结论.
18.观察与计算:
152=225=1×2×100+25;
252=625=2×3×100+25;
352=1225=3×4×100+25;
…
猜想与计算:
852= ,1052= ;
发现:末位数字是5的数的平方的结果总是等于 ;
说理:请你用整式的乘法的有关知识说明你发现的结论的正确性.
(提示:可以用10a+5表示末位数字是5的数)
19.你会求(a﹣1)(a2021+a2020+a2019+…+a2+a+1)的值吗?
这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
(a﹣1)(a+1)=a2﹣1;
(a﹣1)(a2+a+1)=a3﹣1;
(a﹣1)(a3+a2+a+1)=a4﹣1.
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2020+a2019+a2018+…+a2+a+1)= .
利用上面的结论求:
(2)求22020+22019+22018+…+22+2+1的值.
(3)求52020+52019+52018+…+52+4的值.
20.阅读下列材料:小亮为了计算1+2+22+…+22017+22018+22019的值,采用以下方法:
设S=1+2+22+…+22017+22018+22019①;
则2S=2+22+23+…+22018+22019+22020②;
②﹣①得2S﹣S=(2+22+23+…+22018+22019+22020)﹣(1+2+22+…+22017+22018+22019);
∴S=2+22+23+…+22018+22019+22020﹣1﹣2﹣22﹣…﹣22017﹣22018﹣22019;
∴S=22020﹣1;
∴1+2+22+…+22017+22018+22019=22020﹣1.
请仿照小亮的方法解决以下问题:
(1)1+2+22+…+29+210= ;
(2)1+3+32+…+399= ;
(3)求1+a+a2+…+an的值(a>0,n是正整数,请写出计算过程).
参考答案
1.解:(1)由图形的变化规律知,④中黑三角的个数为1+2+3+4=10,
中黑三角的个数为1+2+3+4+...+n=n(n+1),
故答案为:10,n(n+1);
(2)由(1)的规律知,n(n+1)=91,
∵n>0,
∴n=13.
2.解:(1)根据图形的变化可知:第(7)个等式为:(1+2+3+4+5+6)×2+7=72;
所以第n个图形的规律为:(1+2+3+...+n﹣1)×2+n=n2;
故答案为:(1+2+3+4+5+6)×2+7=72;(1+2+3+...+n﹣1)×2+n=n2;
(2)因为(1+2+3+4+...+80)×2+81=812,
(1+2+3+4+..+9)×2+10=102,
1+2+3+4+...+80==3240,
1+2+3+4+...+9==45,
所以10+11+…+80=(1+2+3+4+...+80)﹣(1+2+3+4+...+9)=3195.
3.解:(1)写出第6个等式:62=7×5+1;
故答案为:62=7×5+1;
(2)猜想的第n个等式:n2=(n+1)(n﹣1)+1,
证明:左边=n2,右边=n2﹣1+1=n2,
∴左=右,
∴原题得证.
故答案为:n2=(n+1)(n﹣1)+1.
4.解:(1)按图示规律填空:
图形标号 ① ② ③ ④ ⑤
火柴棒根数 5 9 13 17 21
故答案为:17,21;
(2)由(1)可得出规律:4n+1,
即照这样的规律摆下去,搭第n个图形需要4n+1根火柴棒;
故答案为:4n+1;
(3)当n=2021时,4×2021+1=8085,
所以第2021个图形需要的火柴棒8085根.
5.解:(1)根据题意得,
第一层有2×1﹣1=1个白色棋子,
第二层有2×2﹣1=3个白色棋子,
第三层有2×3﹣1=5个白色棋子,
第四层有2×4﹣1=7个白色棋子,
…,
∴第n层由2n﹣1(个)白色棋子;
从第一层到第二层共有1+3=4=22个白色棋子;
从第一层到第三层共有1+3+5=9=32个白色棋子;
从第一层到第四层共有1+3+5+7=16=42个白色棋子;
∴图中从第一层到第n层一共有 1+3+5+7+ +(2n﹣1)=n2(个)白色棋子;
故答案为:(2n﹣1);n2.
(2)1921+1923+1925+…+2021
=(1+3+5+7+ +2021)﹣(1+3+5+7+ +1919)
=10112﹣9602
=100521.
6.解:(1)尝试:3×1+1=4,
3×2+1=7;
3×3+1=10;
3×4+1=13;
3×5+1=16;
3×100+1=301;
故答案为:16,301;
(2)发现:通过尝试可知:第n个操作后,分割成的正方形个数为:3n+1;
设每个操作后得到互不重叠的正方形的个数为m,则m=3n+1.
若m=2021,则2021=3n+1.解得n=,这个数不是整数,故不能.
7.解:(1)第5个等式:2+3+4+5+6+5+4+3+2=62﹣2;
故答案为:2+3+4+5+6+5+4+3+2=62﹣2;
(2)第n个等式为:2+3+4+5+6+…+n+(n+1)+n+…+5+4+3+2=(n+1)2﹣2;
证明:已知:1+2+3+…+n=,
∴2+3+…+n=﹣1.
∵2+3+4+5+6+…+n+(n+1)+n+…+5+4+3+2=(n+1)2﹣2
=2[﹣1]+n+1
=n2+n﹣2+n+1
=n2+2n﹣1
=n2+2n+1﹣1﹣1
=(n+1)2﹣2.
故答案为:2+3+4+5+6+…+n+(n+1)+n+…+5+4+3+2=(n+1)2﹣2.
8.解:(1)观察图形规律:
第一个图形有4个五角星,
第二个图形比第一个图形多3个五角星,即有4+3=7个五角星,
第三个图形比第二个图形多3个五角星,即有4+3+3=10个五角星,
第四个图形比第三个图形多3个五角星,即有4+3+3+3=13个五角星,
…………
以此类推,第n个图形中的五角星有4+3(n﹣1)=(3n+1)个五角星,
故答案为:10,13,3n+1;
(2)将n=20代入3n+1中,得3×20+1=61(个),
故答案为:61;
(3)假设存在第n个图案,恰好含有2021个五角星.
依题意可得3n+1=2021,
解得n=673……1,
∵n为正整数才符合题意,
∴不存在恰好含有2021个五角星的图案.
(4)前20个五角星图案中,五角星的总个数为:
4+7+10+13+……+58+61
=(4+61)+(7+58)+……+(31+34)
=65+65+……+65
=65×10
=650(个),
∴前20个五角星图案中,五角星的总个数为650个.
9.解:(1)n=1时,有5个,即3×1+2(个);
n=2时,有8个,即3×2+2(个);
n=3时,有11个,即3×3+2(个);
n=4时,有3×4+2=14(个);
故答案为:14.
(2)由题意知,第n个图形中有三角形(3n+2)个,
故答案为:3n+2;
(3)当n=2021时,3×2021+2=6065,
故答案为:6065.
10.解:(Ⅰ)观察图形的变化可知:
当n=2时,S的值为3=3×1;
当n=3时,S的值为6=3×2;
当n=4时,S的值为9=3×3;
当n=5时,S的值为12=3×4;
当n=6时,S的值为15=3×5;
故答案为:9;15;
(Ⅱ)由(Ⅰ)知:
每条“边”有n个点时的总点数S是3(n﹣1);
故答案为:3(n﹣1);
(Ⅲ)当n=2021时,总点数S=3(2021﹣1)=6060.
11.解:(1)设第一种摆放方式n张桌子能坐an人,第二种摆放方式n张桌子能坐bn人.
∵a1=6=4×1+2,a2=10=4×2+2,a3=14=4×3+2,…,
∴an=4n+2;
同理,可得出:bn=2n+4.
∴第一种摆放方式能坐(4n+2)人,第二种摆放方式能坐(2n+4)人.
(2)当n=18时,an=4n+2=74,bn=2n+4=40.
∵74>73,40<73,
∴应该选择第一种摆放方式来摆放餐桌.
12.(1)由题意得:第④个等式为:1+3+5+7=42,
第⑤个等式为:1+3+5+7+9=52,
故答案为:1+3+5+7=42;1+3+5+7+9=52;
(2)∵①1=12;
②1+3=22;
③1+3+5=32;
④1+3+5+7=42;
⑤1+3+5+7+9=52;
...
∴第n个星阵图对应的等式为:1+3+5+ +(2n﹣1)=n2.
13.解:(1)由图可知,图2、图3中三角形的个数分别为5个,9个;
故答案为:5,9;
(2)由(1)可知:图1中三角形的个数为1个,
图2中三角形的个数为5个,
图3中三角形的个数为9个,
由于每次三角形递增4个,所以第n个图形中有1+4(n﹣1)=(4n﹣3)个三角形,
4n﹣3=2019,
解得:n=,
∵n的值不是整数,
∴不存在2019个三角形.
14.解:(1)观察图形可知:部分①的面积为:,
部分②的面积为=,
部分③的面积为=,
故答案为:,,;
(2)阴影部分的面积是=;
(3)①由(1)知:=1﹣,
故答案为:1﹣;
②当n=10时,
方法一:由①知:的值为:1﹣;
方法二:原式=1﹣+﹣+﹣+…+﹣=1﹣.
15.解:(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.
即第n个图案需要5+3(n﹣1)=3n+2.
那么当n=3时,则有11枚;当n=4时,则有14枚;当n=10时,则有32枚;
填表如下:
图形序号 ① ② ③ ④ … ⑩
每个图案中棋子个数 5 8 11 14 … 32
故答案为:11,14,32.
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需5+3×(n﹣1)=5+3n﹣3=(3n+2)枚棋子.
故答案为:(3n+2);
(3)第20个“T”字形图案共有棋子3×20+2=62(个).
即第20个图案需62个棋子;
(4)前20个“T”字形图案中棋子的总个数为:
5+8+11+14+17+…+53+56+59+62
=(5+62)+(8+59)+(11+56)+…+(32+35)
=67×10
=670(个).
故答案是:670.
16.解:(1);;
故答案为:﹣,﹣;
(2);
(3).
17.解:(1)原式=×(1﹣)+×(﹣)+×(﹣)+×(﹣)+…+×(﹣)
=(1﹣+﹣+﹣+﹣+…+﹣)
=(1﹣)
=;
故答案为:;
(2)根据题意可知:=×(﹣).
故答案为:×(﹣).
18.解:852=8×9×100+25=7225;
1052=10×11×100+25=11025;
发现:末位数字是5的数的平方的结果总是等于去掉5得到的数与比这个数大1的数的积的100倍加上25;
故答案为:7225,11025,去掉5得到的数与比这个数大1的数的积的100倍加上25;
说理:设末位数字的是5的数为10a+5,则
(10a+5)2=100a2+100a+25
=100a(a+1)+25.
故以上计算正确.
19.解:(1)∵(a﹣1)(a+1)=a2﹣1;
(a﹣1)(a2+a+1)=a3﹣1;
(a﹣1)(a3+a2+a+1)=a4﹣1.
∴(a﹣1)(a2020+a2019+a2018+…+a2+a+1)=a2021﹣1.
故答案为:a2021﹣1.
(2)∵(a﹣1)(a2020+a2019+a2018+…+a2+a+1)=a2021﹣1.
当a=2时,22020+22019+22018+…+22+2+1
=(2﹣1)×(22020+22019+22018+…+22+2+1)
=22021﹣1.
(3)∵(a﹣1)(a2020+a2019+a2018+…+a2+a+1)=a2021﹣1.
当a=5时,(5﹣1)×(52020+52019+52018+…+52+5+1)=52021﹣1,
∴52020+52019+52018+…+52+5+1=(52021﹣1),
∴52020+52019+52018+…+52+4
=52020+52019+52018+…+52+5+1﹣2
=(52021﹣1)﹣2
=.
20.解:(1)设S=1+2+22+……+210①,
则2S=2+22+……+211②,
②﹣①得,2S﹣S=S=211﹣1,
即S=211﹣1.
故答案为:211﹣1.
(2)设S=3+32+……+399,①
则3S=32+33+……+3100,②
②﹣①得,3S﹣S=2S=3100﹣3,
∴S=.
故答案为:.
(3)当a=1时,原式=n+1;
当a≠1时,
令S=1+a+a2+……+an,①
则aS=a+a2+……+an+1,②
②﹣①得,aS﹣S=(a﹣1)S=an+1﹣1,
∴S=.(a≠1)
综上所述:
当a=1时,原式=n+1;
当a≠1时,原式=1+a+a2+……+an=
1.把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形…按此规律排列下去,解答下列问题:
(1)填写下列表格:
图序 ① ② ③ ④ …
黑色三角形个数 1 3 6 …
(2)若第 个图案中黑色三角形的个数有91个,求n的值.
2.观察下列图形与等式:
(1)观察图形,写出第(7)个等式: ;根据图中规律,写出第n个图形的规律: ;(用含有n的式子表示)
(2)求出10+11+…+80的值.
3.如图,是一组完全相同的黑白小球组成的图形:
观察上面各图及对应的关系式,根据发现的规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示,并证明其正确性).
4.用火柴棒按图中的方式搭图形:
按图示规律填空:
图形标号 ① ② ③ ④ ⑤
火柴棒根数 5 9 13 a b
(1)a= ,b= ;
(2)按照这种方式搭下去,则搭第n个图形需要火柴棒的根数为 ;(用含n的代数式来表示)
(3)按照这种方式搭下去,用(2)中的代数式求第2021个图形需要的火柴棒根数.
5.将围棋的白色棋子按如图所示的方式排列,图中的白色棋子被折线隔开分成若干层,第一层有1个白色棋子,第二层有3个白色棋子,第三层有5个白色棋子,第四层有7个白色棋子,…,以此类推,请观察图形规律,解答下列问题:
(1)第n层有 个白色棋子,图中从第一层到第n层一共有 个白色棋子;
(2)利用发现的规律计算:1921+1923+1925+…+2021的和.
6.如图1,给定一个正方形,要通过裁剪将其分割成若干个互不重叠的正方形.第1次裁剪分割成4个互不重叠的正方形,得到图2,称之为1个基本操作;第2次裁剪分割成7个互不重叠的正方形,得到图3,称之为2个基本操作…以后每次只在上次得到图形的左上角的正方形中裁剪.
(1)5个基本操作后,共裁剪成 个正方形;100个基本操作后,共裁剪成 个正方形;
(2)经过若干次基本操作后,能否得到2021个互不重叠的正方形?若能,求出是几个基本操作后得到的;若不能,请说明理由.
7.观察下列图形与等式的关系:
按照以上图形与等式的规律,解答下列问题:
(1)写出第5个等式: .
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明(已知:1+2+3+…+n=).
8.按如下规律摆放五角星:
(1)填写表格:
图案序号 1 2 3 4 … n
五角星个数 4 7 …
(2)直接写出第20个图案的五角星个数,个数为 ;
(3)若按上面的规律继续摆放,是否存在某个图案,其中恰好含有2021个五角星?
(4)计算前20个五角星图案中五角星的总个数.
9.按如下规律摆放三角形:
(1)图④中分别有 个三角形?
(2)按上述规律排列下去,第n个图形中有 个三角形?
(3)按上述规律排列下去,第2021个图形中有 个三角形?
10.如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有n(n>1)个点,每个图形的总点数记为S.
(Ⅰ)当n=4时,S的值为 ;当n=6时,S的值为 ;
(Ⅱ)每条“边”有n个点时的总点数S是 (用含n的式子表示);
(Ⅲ)当n=2021时,总点数S是多少?
11.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待73位顾客且要“同桌”就餐,但餐厅只有18张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
12.找规律:观察下面的星阵图和相应的等式,探究其中的规律.
(1)在④和⑤后面的横线上分别写出相应的等式:
①1=12;
②1+3=22;
③1+3+5=32;
④ ;
⑤ ;
(2)通过猜想,写出第n个星阵图相对应的等式.
13.图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形三边的中点,得到图3.
(1)图2中共有 个三角形,图3中共有 个三角形;
(2)按上面的方法继续下去,第n个图形(图1是第一个图形)中共有多少个三角形(用含n的代数式表示)?是否存在2019个三角形?若存在,求出n的值,若不存在,说明理由.
14.如图所示,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分⑧是部分②面积的一半,依此类推…
(1)根据图形填写下表;
① ② ③
面积
(2)阴影部分的面积是多少?
(3)猜想:①= ;
②当n=10时,请用两种方法计算:的值(结果用分数表示).
15.如图所示的是用棋子摆成的“T”字形图案.
(1)填写表:
图案序号 ① ② ③ ④ … ⑩
每个图案中棋子的个数 5 8 …
(2)第n个“T”字形图案中棋子的个数为 .(用含n的代数式表示)
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数为 .
16.观察下列各等式,并回答问题:
,,,,….
(1)填空:= ;= (n为整数);
(2)计算:;
(3)计算:.
17.观察下面的等式:
第1个等式:=×(1﹣);
第2个等式:=×(﹣);
第3个等式:=×(﹣);
第4个等式:=×(﹣);
…
解答下面的问题:
(1)+++…+= ;
(2)若n为正整数,请你猜想= ,并证明你猜想的结论.
18.观察与计算:
152=225=1×2×100+25;
252=625=2×3×100+25;
352=1225=3×4×100+25;
…
猜想与计算:
852= ,1052= ;
发现:末位数字是5的数的平方的结果总是等于 ;
说理:请你用整式的乘法的有关知识说明你发现的结论的正确性.
(提示:可以用10a+5表示末位数字是5的数)
19.你会求(a﹣1)(a2021+a2020+a2019+…+a2+a+1)的值吗?
这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
(a﹣1)(a+1)=a2﹣1;
(a﹣1)(a2+a+1)=a3﹣1;
(a﹣1)(a3+a2+a+1)=a4﹣1.
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2020+a2019+a2018+…+a2+a+1)= .
利用上面的结论求:
(2)求22020+22019+22018+…+22+2+1的值.
(3)求52020+52019+52018+…+52+4的值.
20.阅读下列材料:小亮为了计算1+2+22+…+22017+22018+22019的值,采用以下方法:
设S=1+2+22+…+22017+22018+22019①;
则2S=2+22+23+…+22018+22019+22020②;
②﹣①得2S﹣S=(2+22+23+…+22018+22019+22020)﹣(1+2+22+…+22017+22018+22019);
∴S=2+22+23+…+22018+22019+22020﹣1﹣2﹣22﹣…﹣22017﹣22018﹣22019;
∴S=22020﹣1;
∴1+2+22+…+22017+22018+22019=22020﹣1.
请仿照小亮的方法解决以下问题:
(1)1+2+22+…+29+210= ;
(2)1+3+32+…+399= ;
(3)求1+a+a2+…+an的值(a>0,n是正整数,请写出计算过程).
参考答案
1.解:(1)由图形的变化规律知,④中黑三角的个数为1+2+3+4=10,
中黑三角的个数为1+2+3+4+...+n=n(n+1),
故答案为:10,n(n+1);
(2)由(1)的规律知,n(n+1)=91,
∵n>0,
∴n=13.
2.解:(1)根据图形的变化可知:第(7)个等式为:(1+2+3+4+5+6)×2+7=72;
所以第n个图形的规律为:(1+2+3+...+n﹣1)×2+n=n2;
故答案为:(1+2+3+4+5+6)×2+7=72;(1+2+3+...+n﹣1)×2+n=n2;
(2)因为(1+2+3+4+...+80)×2+81=812,
(1+2+3+4+..+9)×2+10=102,
1+2+3+4+...+80==3240,
1+2+3+4+...+9==45,
所以10+11+…+80=(1+2+3+4+...+80)﹣(1+2+3+4+...+9)=3195.
3.解:(1)写出第6个等式:62=7×5+1;
故答案为:62=7×5+1;
(2)猜想的第n个等式:n2=(n+1)(n﹣1)+1,
证明:左边=n2,右边=n2﹣1+1=n2,
∴左=右,
∴原题得证.
故答案为:n2=(n+1)(n﹣1)+1.
4.解:(1)按图示规律填空:
图形标号 ① ② ③ ④ ⑤
火柴棒根数 5 9 13 17 21
故答案为:17,21;
(2)由(1)可得出规律:4n+1,
即照这样的规律摆下去,搭第n个图形需要4n+1根火柴棒;
故答案为:4n+1;
(3)当n=2021时,4×2021+1=8085,
所以第2021个图形需要的火柴棒8085根.
5.解:(1)根据题意得,
第一层有2×1﹣1=1个白色棋子,
第二层有2×2﹣1=3个白色棋子,
第三层有2×3﹣1=5个白色棋子,
第四层有2×4﹣1=7个白色棋子,
…,
∴第n层由2n﹣1(个)白色棋子;
从第一层到第二层共有1+3=4=22个白色棋子;
从第一层到第三层共有1+3+5=9=32个白色棋子;
从第一层到第四层共有1+3+5+7=16=42个白色棋子;
∴图中从第一层到第n层一共有 1+3+5+7+ +(2n﹣1)=n2(个)白色棋子;
故答案为:(2n﹣1);n2.
(2)1921+1923+1925+…+2021
=(1+3+5+7+ +2021)﹣(1+3+5+7+ +1919)
=10112﹣9602
=100521.
6.解:(1)尝试:3×1+1=4,
3×2+1=7;
3×3+1=10;
3×4+1=13;
3×5+1=16;
3×100+1=301;
故答案为:16,301;
(2)发现:通过尝试可知:第n个操作后,分割成的正方形个数为:3n+1;
设每个操作后得到互不重叠的正方形的个数为m,则m=3n+1.
若m=2021,则2021=3n+1.解得n=,这个数不是整数,故不能.
7.解:(1)第5个等式:2+3+4+5+6+5+4+3+2=62﹣2;
故答案为:2+3+4+5+6+5+4+3+2=62﹣2;
(2)第n个等式为:2+3+4+5+6+…+n+(n+1)+n+…+5+4+3+2=(n+1)2﹣2;
证明:已知:1+2+3+…+n=,
∴2+3+…+n=﹣1.
∵2+3+4+5+6+…+n+(n+1)+n+…+5+4+3+2=(n+1)2﹣2
=2[﹣1]+n+1
=n2+n﹣2+n+1
=n2+2n﹣1
=n2+2n+1﹣1﹣1
=(n+1)2﹣2.
故答案为:2+3+4+5+6+…+n+(n+1)+n+…+5+4+3+2=(n+1)2﹣2.
8.解:(1)观察图形规律:
第一个图形有4个五角星,
第二个图形比第一个图形多3个五角星,即有4+3=7个五角星,
第三个图形比第二个图形多3个五角星,即有4+3+3=10个五角星,
第四个图形比第三个图形多3个五角星,即有4+3+3+3=13个五角星,
…………
以此类推,第n个图形中的五角星有4+3(n﹣1)=(3n+1)个五角星,
故答案为:10,13,3n+1;
(2)将n=20代入3n+1中,得3×20+1=61(个),
故答案为:61;
(3)假设存在第n个图案,恰好含有2021个五角星.
依题意可得3n+1=2021,
解得n=673……1,
∵n为正整数才符合题意,
∴不存在恰好含有2021个五角星的图案.
(4)前20个五角星图案中,五角星的总个数为:
4+7+10+13+……+58+61
=(4+61)+(7+58)+……+(31+34)
=65+65+……+65
=65×10
=650(个),
∴前20个五角星图案中,五角星的总个数为650个.
9.解:(1)n=1时,有5个,即3×1+2(个);
n=2时,有8个,即3×2+2(个);
n=3时,有11个,即3×3+2(个);
n=4时,有3×4+2=14(个);
故答案为:14.
(2)由题意知,第n个图形中有三角形(3n+2)个,
故答案为:3n+2;
(3)当n=2021时,3×2021+2=6065,
故答案为:6065.
10.解:(Ⅰ)观察图形的变化可知:
当n=2时,S的值为3=3×1;
当n=3时,S的值为6=3×2;
当n=4时,S的值为9=3×3;
当n=5时,S的值为12=3×4;
当n=6时,S的值为15=3×5;
故答案为:9;15;
(Ⅱ)由(Ⅰ)知:
每条“边”有n个点时的总点数S是3(n﹣1);
故答案为:3(n﹣1);
(Ⅲ)当n=2021时,总点数S=3(2021﹣1)=6060.
11.解:(1)设第一种摆放方式n张桌子能坐an人,第二种摆放方式n张桌子能坐bn人.
∵a1=6=4×1+2,a2=10=4×2+2,a3=14=4×3+2,…,
∴an=4n+2;
同理,可得出:bn=2n+4.
∴第一种摆放方式能坐(4n+2)人,第二种摆放方式能坐(2n+4)人.
(2)当n=18时,an=4n+2=74,bn=2n+4=40.
∵74>73,40<73,
∴应该选择第一种摆放方式来摆放餐桌.
12.(1)由题意得:第④个等式为:1+3+5+7=42,
第⑤个等式为:1+3+5+7+9=52,
故答案为:1+3+5+7=42;1+3+5+7+9=52;
(2)∵①1=12;
②1+3=22;
③1+3+5=32;
④1+3+5+7=42;
⑤1+3+5+7+9=52;
...
∴第n个星阵图对应的等式为:1+3+5+ +(2n﹣1)=n2.
13.解:(1)由图可知,图2、图3中三角形的个数分别为5个,9个;
故答案为:5,9;
(2)由(1)可知:图1中三角形的个数为1个,
图2中三角形的个数为5个,
图3中三角形的个数为9个,
由于每次三角形递增4个,所以第n个图形中有1+4(n﹣1)=(4n﹣3)个三角形,
4n﹣3=2019,
解得:n=,
∵n的值不是整数,
∴不存在2019个三角形.
14.解:(1)观察图形可知:部分①的面积为:,
部分②的面积为=,
部分③的面积为=,
故答案为:,,;
(2)阴影部分的面积是=;
(3)①由(1)知:=1﹣,
故答案为:1﹣;
②当n=10时,
方法一:由①知:的值为:1﹣;
方法二:原式=1﹣+﹣+﹣+…+﹣=1﹣.
15.解:(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.
即第n个图案需要5+3(n﹣1)=3n+2.
那么当n=3时,则有11枚;当n=4时,则有14枚;当n=10时,则有32枚;
填表如下:
图形序号 ① ② ③ ④ … ⑩
每个图案中棋子个数 5 8 11 14 … 32
故答案为:11,14,32.
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需5+3×(n﹣1)=5+3n﹣3=(3n+2)枚棋子.
故答案为:(3n+2);
(3)第20个“T”字形图案共有棋子3×20+2=62(个).
即第20个图案需62个棋子;
(4)前20个“T”字形图案中棋子的总个数为:
5+8+11+14+17+…+53+56+59+62
=(5+62)+(8+59)+(11+56)+…+(32+35)
=67×10
=670(个).
故答案是:670.
16.解:(1);;
故答案为:﹣,﹣;
(2);
(3).
17.解:(1)原式=×(1﹣)+×(﹣)+×(﹣)+×(﹣)+…+×(﹣)
=(1﹣+﹣+﹣+﹣+…+﹣)
=(1﹣)
=;
故答案为:;
(2)根据题意可知:=×(﹣).
故答案为:×(﹣).
18.解:852=8×9×100+25=7225;
1052=10×11×100+25=11025;
发现:末位数字是5的数的平方的结果总是等于去掉5得到的数与比这个数大1的数的积的100倍加上25;
故答案为:7225,11025,去掉5得到的数与比这个数大1的数的积的100倍加上25;
说理:设末位数字的是5的数为10a+5,则
(10a+5)2=100a2+100a+25
=100a(a+1)+25.
故以上计算正确.
19.解:(1)∵(a﹣1)(a+1)=a2﹣1;
(a﹣1)(a2+a+1)=a3﹣1;
(a﹣1)(a3+a2+a+1)=a4﹣1.
∴(a﹣1)(a2020+a2019+a2018+…+a2+a+1)=a2021﹣1.
故答案为:a2021﹣1.
(2)∵(a﹣1)(a2020+a2019+a2018+…+a2+a+1)=a2021﹣1.
当a=2时,22020+22019+22018+…+22+2+1
=(2﹣1)×(22020+22019+22018+…+22+2+1)
=22021﹣1.
(3)∵(a﹣1)(a2020+a2019+a2018+…+a2+a+1)=a2021﹣1.
当a=5时,(5﹣1)×(52020+52019+52018+…+52+5+1)=52021﹣1,
∴52020+52019+52018+…+52+5+1=(52021﹣1),
∴52020+52019+52018+…+52+4
=52020+52019+52018+…+52+5+1﹣2
=(52021﹣1)﹣2
=.
20.解:(1)设S=1+2+22+……+210①,
则2S=2+22+……+211②,
②﹣①得,2S﹣S=S=211﹣1,
即S=211﹣1.
故答案为:211﹣1.
(2)设S=3+32+……+399,①
则3S=32+33+……+3100,②
②﹣①得,3S﹣S=2S=3100﹣3,
∴S=.
故答案为:.
(3)当a=1时,原式=n+1;
当a≠1时,
令S=1+a+a2+……+an,①
则aS=a+a2+……+an+1,②
②﹣①得,aS﹣S=(a﹣1)S=an+1﹣1,
∴S=.(a≠1)
综上所述:
当a=1时,原式=n+1;
当a≠1时,原式=1+a+a2+……+an=
