2021-2022学年人教版数学 七年级上册4.4 课题学习 设计制作长方体形状的包装纸盒课件(43张)
文档属性
| 名称 | 2021-2022学年人教版数学 七年级上册4.4 课题学习 设计制作长方体形状的包装纸盒课件(43张) |

|
|
| 格式 | zip | ||
| 文件大小 | 892.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 12:11:17 | ||
图片预览





文档简介
(共43张PPT)
人教版数学 七年级上册
第四章 几何图形初步
4.4 课题学习
设计制作长方体形状的包装纸盒
“鲁班锁”是一种立体插接玩具,是由中国
古代房屋的榫卯结构转化而来的,因为鲁班是中
国木工的始祖,所以得名“鲁班锁”.“鲁班锁”
一般由六根短木组成,中间有缺,缺缺结合,以十字双交卡榫组成.将木块大小不一的卡榫精准放置才能组合成功,而且只要抽掉一根木条,整个接合的木块就会散架.古老的中国智慧对今天我们所学内容有什么启示呢
导入新知
1. 通过问题的解决进一步理解立体图形和相应平面图形之间的转化关系.
2. 通过包装纸盒的制作,掌握制作长方体纸盒的一般方法,能够独立制作出相关的包装盒.
学习目标
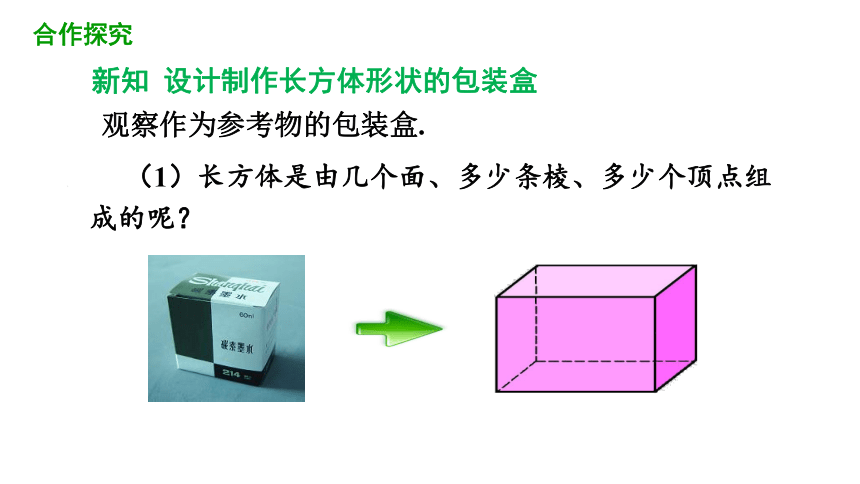
观察作为参考物的包装盒.
(1)长方体是由几个面、多少条棱、多少个顶点组成的呢?
新知 设计制作长方体形状的包装盒
合作探究
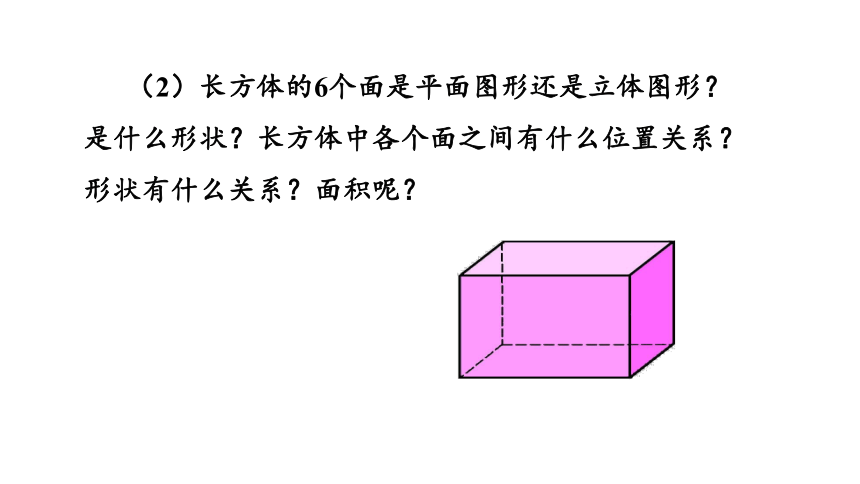
(2)长方体的6个面是平面图形还是立体图形?是什么形状?长方体中各个面之间有什么位置关系?形状有什么关系?面积呢?
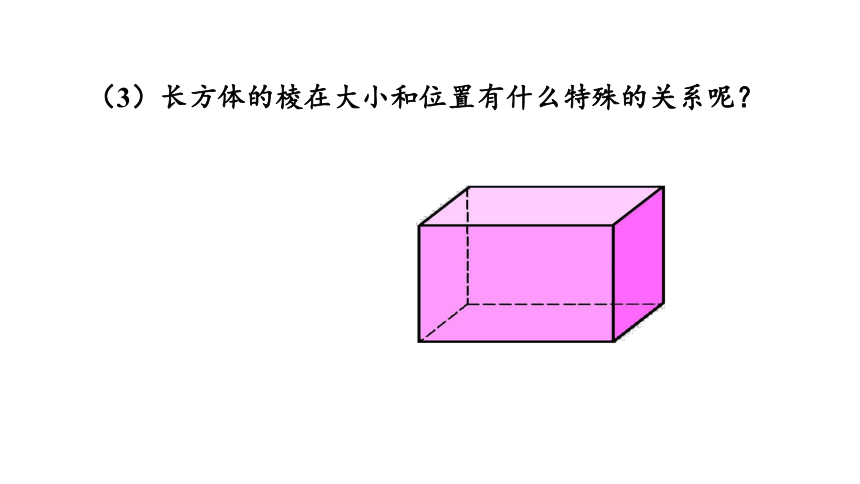
(3)长方体的棱在大小和位置有什么特殊的关系呢?
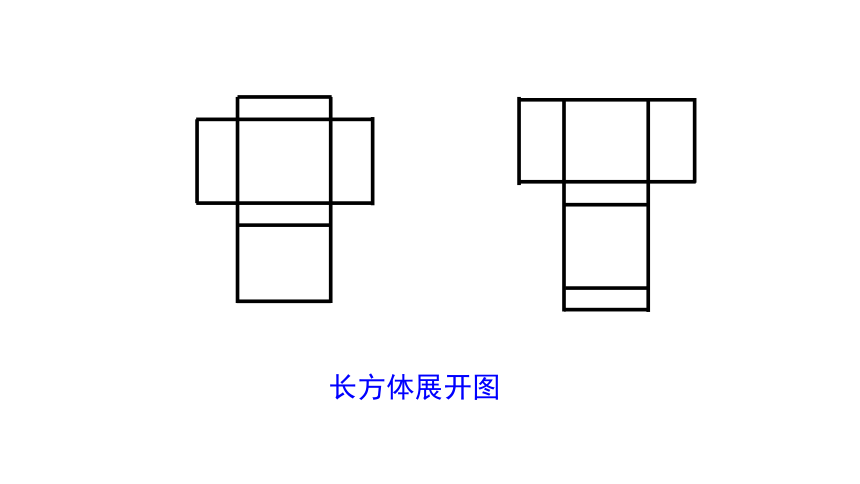
拆开观察长方体包装盒的展开图.
展开
(1)将每一组的纸制长方体沿棱剪开,展开成一个完整的平面展开图,需要剪开多少条棱?
长方体展开图
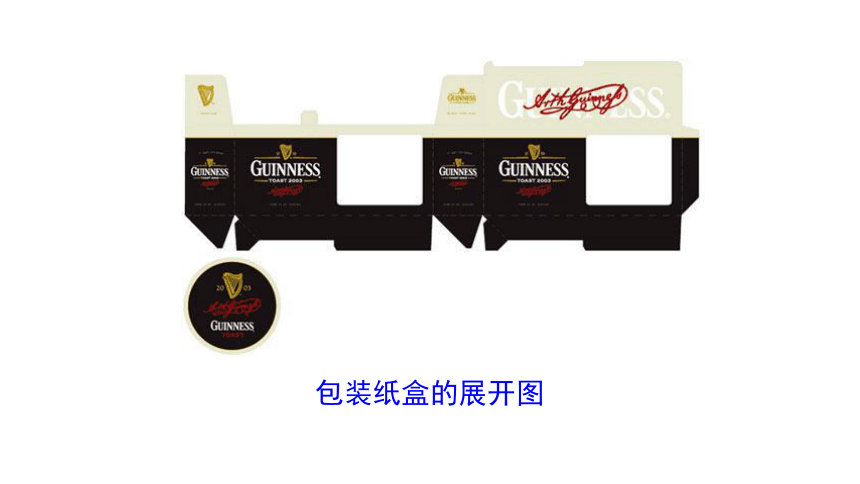
包装纸盒的展开图
包装纸盒的展开图
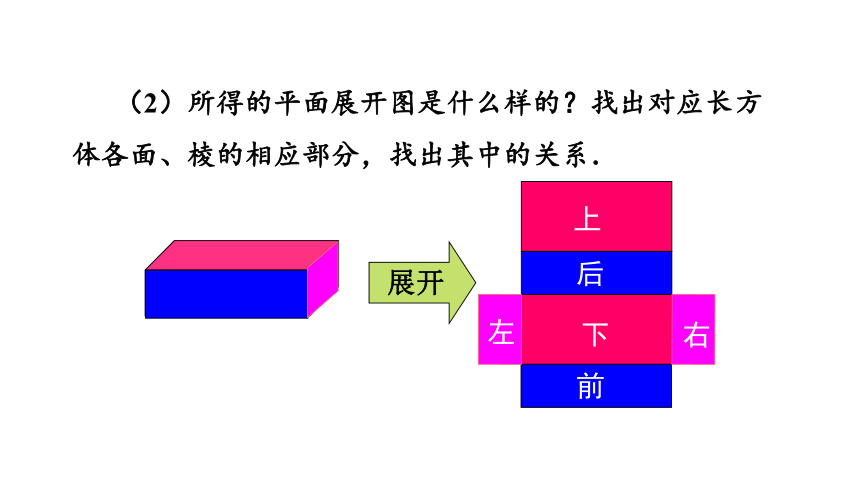
(2)所得的平面展开图是什么样的?找出对应长方体各面、棱的相应部分,找出其中的关系.
上
下
后
前
左
右
展开
上
前
后
左
右
展开
下
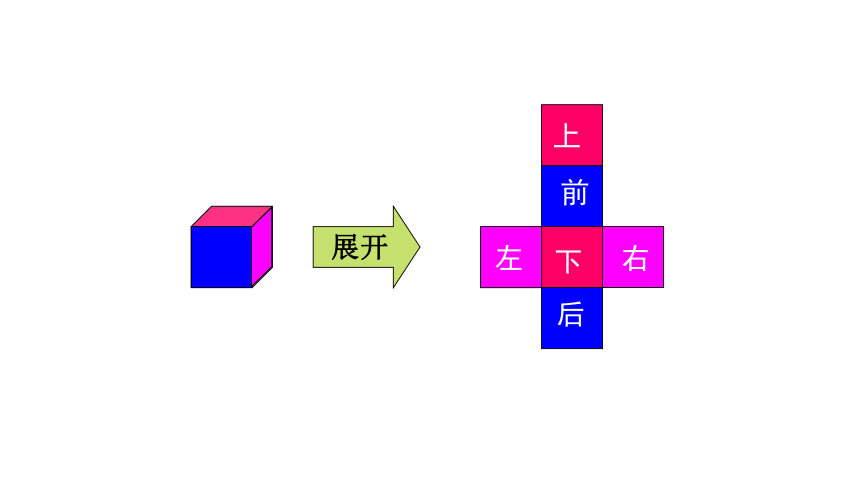
(3) 展示所得的图形,并说明展开图与立体图形之间的联系.
上
下
后
前
左
右
展开
上
下
前
后
左
右
展开
观察它是如何折叠并粘到一起的.
还原表面展开图为包装盒.
折叠
经过讨论,确定本组的设计方案.
包装盒的形状、尺寸、外表图案等.
设计方案内容包括:
素养考点
设计制作长方体形状的包装盒
设计
设计、制作出如图所示的纸盒.
4厘米
3厘米
5厘米
1
先在一张软纸上画出包装盒平面展开图的草图;设计时要仔细观察后再裁纸、折叠.
步骤
在硬纸板上,按照初步设计,画好包装盒的平面展开图,注意要预留出黏合处,并要适当剪去棱角.在平面展开图上进行图案与文字的美术设计.
2
步骤
裁下平面展开图,折叠并粘好黏合处,得到长方体包装盒.
3
各小组展示成果.
步骤
1.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是 ( )
C
A.
D.
C.
B.
2.下面每个图形都是由6个边长相同的正方形拼成的图形,其中能折叠成正方体的是( )
A. B. C. D.
C
3.将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是 ( )
A.庆 B.力
C.大 D.魅
A
制作立体图形时,要先将立体图转化为平面图形(平面展开图),再转化为立体图形(折叠).
归纳新知
1.若∠AOB=40°,∠BOC=20°,则∠AOC的度数为( )
A.60°
B.20°
C.20°或60°
D.40°或80°
C
课后练习
6cm或18cm
3.已知平面内有A,B,C,D四个点,过其中任意两点画一条直线,最多可以画出几条直线?请你画图说明.
解:①当A,B,C,D四个点在同一条直线上时,只能画出一条直线,如图1所示;②当A,B,C,D四个点中有三个点在同一条直线上(假设B,C,D三点在同一条直线上)时,可以画出4条直线,如图2所示;③当A,B,C,D四个点中任意三个点都不在同一条直线上时,可以画出6条直线,如图3所示.综上所述,最多可以画出1或4或6条直线.
4.已知线段AB=12 cm,直线AB上有一点C,且BC=6 cm,M是线段AC的中点,求线段AM 的长.
5.已知:如图,OC是∠AOB的平分线.
(1)当∠AOB=60°时,求∠AOC的度数;
(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;
(3)当∠AOB=α,∠EOC=90°时,直接写出∠AOE的度数.(用含α的式子表示)
7.如图,线段AB上顺次有三个点C,D,E,把线段AB分为2∶3∶4∶5四部分,且AB=28.
(1)求线段AE的长;
(2)若M,N分别是DE,EB的中点,求线段MN的长度.
8.如图,∠AOC和∠BOD都是直角.
(1)图中与∠BOC互余的角有_______和________;
(2)∠AOD与∠BOC互补吗?为什么?
(3)若∠AOB∶∠AOD=3∶13,求∠BOC与∠AOD的度数.
∠AOB
∠COD
解:(2)∠AOD与∠BOC互补,理由:因为∠AOC和∠BOD都是直角,所以∠AOB+∠BOC=∠COD+∠BOC=90°,又因为∠AOD=∠AOB+∠BOC+∠COD,所以∠AOD+∠BOC=∠AOB+∠BOC+∠COD+∠BOC=∠AOC+∠BOD=180°,所以∠AOD与∠BOC互补.
(3)设∠AOB=3x°,则∠AOD=13x°,所以∠BOD=∠AOD-∠AOB=13x-3x=10x=90,解得x=9,所以∠AOD=13x°=117°,由(2)可知∠AOD与∠BOC互补,所以∠BOC=180°-117°=63°.
9.如图,已知点C,D在线段AB上,M,N分别是AC,BD的中点.
(1)若AB=20,CD=4,求MN的长;
(2)若AB=a,CD=b,请用含有a,b的式子表示出MN的长.
再 见
人教版数学 七年级上册
第四章 几何图形初步
4.4 课题学习
设计制作长方体形状的包装纸盒
“鲁班锁”是一种立体插接玩具,是由中国
古代房屋的榫卯结构转化而来的,因为鲁班是中
国木工的始祖,所以得名“鲁班锁”.“鲁班锁”
一般由六根短木组成,中间有缺,缺缺结合,以十字双交卡榫组成.将木块大小不一的卡榫精准放置才能组合成功,而且只要抽掉一根木条,整个接合的木块就会散架.古老的中国智慧对今天我们所学内容有什么启示呢
导入新知
1. 通过问题的解决进一步理解立体图形和相应平面图形之间的转化关系.
2. 通过包装纸盒的制作,掌握制作长方体纸盒的一般方法,能够独立制作出相关的包装盒.
学习目标
观察作为参考物的包装盒.
(1)长方体是由几个面、多少条棱、多少个顶点组成的呢?
新知 设计制作长方体形状的包装盒
合作探究
(2)长方体的6个面是平面图形还是立体图形?是什么形状?长方体中各个面之间有什么位置关系?形状有什么关系?面积呢?
(3)长方体的棱在大小和位置有什么特殊的关系呢?
拆开观察长方体包装盒的展开图.
展开
(1)将每一组的纸制长方体沿棱剪开,展开成一个完整的平面展开图,需要剪开多少条棱?
长方体展开图
包装纸盒的展开图
包装纸盒的展开图
(2)所得的平面展开图是什么样的?找出对应长方体各面、棱的相应部分,找出其中的关系.
上
下
后
前
左
右
展开
上
前
后
左
右
展开
下
(3) 展示所得的图形,并说明展开图与立体图形之间的联系.
上
下
后
前
左
右
展开
上
下
前
后
左
右
展开
观察它是如何折叠并粘到一起的.
还原表面展开图为包装盒.
折叠
经过讨论,确定本组的设计方案.
包装盒的形状、尺寸、外表图案等.
设计方案内容包括:
素养考点
设计制作长方体形状的包装盒
设计
设计、制作出如图所示的纸盒.
4厘米
3厘米
5厘米
1
先在一张软纸上画出包装盒平面展开图的草图;设计时要仔细观察后再裁纸、折叠.
步骤
在硬纸板上,按照初步设计,画好包装盒的平面展开图,注意要预留出黏合处,并要适当剪去棱角.在平面展开图上进行图案与文字的美术设计.
2
步骤
裁下平面展开图,折叠并粘好黏合处,得到长方体包装盒.
3
各小组展示成果.
步骤
1.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是 ( )
C
A.
D.
C.
B.
2.下面每个图形都是由6个边长相同的正方形拼成的图形,其中能折叠成正方体的是( )
A. B. C. D.
C
3.将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是 ( )
A.庆 B.力
C.大 D.魅
A
制作立体图形时,要先将立体图转化为平面图形(平面展开图),再转化为立体图形(折叠).
归纳新知
1.若∠AOB=40°,∠BOC=20°,则∠AOC的度数为( )
A.60°
B.20°
C.20°或60°
D.40°或80°
C
课后练习
6cm或18cm
3.已知平面内有A,B,C,D四个点,过其中任意两点画一条直线,最多可以画出几条直线?请你画图说明.
解:①当A,B,C,D四个点在同一条直线上时,只能画出一条直线,如图1所示;②当A,B,C,D四个点中有三个点在同一条直线上(假设B,C,D三点在同一条直线上)时,可以画出4条直线,如图2所示;③当A,B,C,D四个点中任意三个点都不在同一条直线上时,可以画出6条直线,如图3所示.综上所述,最多可以画出1或4或6条直线.
4.已知线段AB=12 cm,直线AB上有一点C,且BC=6 cm,M是线段AC的中点,求线段AM 的长.
5.已知:如图,OC是∠AOB的平分线.
(1)当∠AOB=60°时,求∠AOC的度数;
(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;
(3)当∠AOB=α,∠EOC=90°时,直接写出∠AOE的度数.(用含α的式子表示)
7.如图,线段AB上顺次有三个点C,D,E,把线段AB分为2∶3∶4∶5四部分,且AB=28.
(1)求线段AE的长;
(2)若M,N分别是DE,EB的中点,求线段MN的长度.
8.如图,∠AOC和∠BOD都是直角.
(1)图中与∠BOC互余的角有_______和________;
(2)∠AOD与∠BOC互补吗?为什么?
(3)若∠AOB∶∠AOD=3∶13,求∠BOC与∠AOD的度数.
∠AOB
∠COD
解:(2)∠AOD与∠BOC互补,理由:因为∠AOC和∠BOD都是直角,所以∠AOB+∠BOC=∠COD+∠BOC=90°,又因为∠AOD=∠AOB+∠BOC+∠COD,所以∠AOD+∠BOC=∠AOB+∠BOC+∠COD+∠BOC=∠AOC+∠BOD=180°,所以∠AOD与∠BOC互补.
(3)设∠AOB=3x°,则∠AOD=13x°,所以∠BOD=∠AOD-∠AOB=13x-3x=10x=90,解得x=9,所以∠AOD=13x°=117°,由(2)可知∠AOD与∠BOC互补,所以∠BOC=180°-117°=63°.
9.如图,已知点C,D在线段AB上,M,N分别是AC,BD的中点.
(1)若AB=20,CD=4,求MN的长;
(2)若AB=a,CD=b,请用含有a,b的式子表示出MN的长.
再 见
