2021-2022学年人教版数学 八年级上册11.1.3 三角形的稳定性课件(42张)
文档属性
| 名称 | 2021-2022学年人教版数学 八年级上册11.1.3 三角形的稳定性课件(42张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 00:00:00 | ||
图片预览









文档简介
(共42张PPT)
人教版数学 八年级上册
第十一章 三角形
11.1 与三角形有关的线段
11.1.3 三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗
想一想
导入新知
生活小常识
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,如图,为什么要这样做呢?
1. 了解三角形的稳定性和四边形的不稳定性.
2. 了解三角形的稳定性和四边形不稳定性的应用.
学习目标
动手做一做
1. 将三根木条用钉子钉成一个三角形木架.
2. 将四根木条用钉子钉成一个四边形木架.
新知一 三角形的稳定性
合作探究
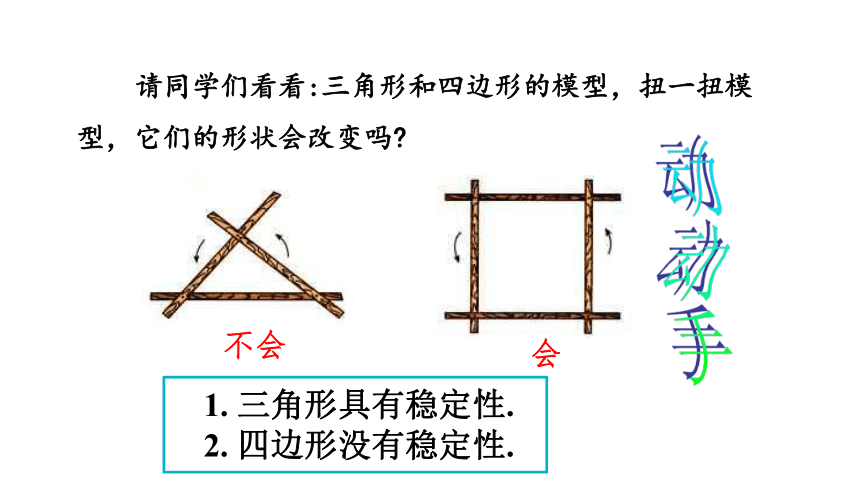
请同学们看看:三角形和四边形的模型,扭一扭模型,它们的形状会改变吗
动动手
不会
会
1. 三角形具有稳定性.
2. 四边形没有稳定性.
理解“稳定性”
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
【思考】你能举出一些现实生活中应用三角形稳定性的例子吗
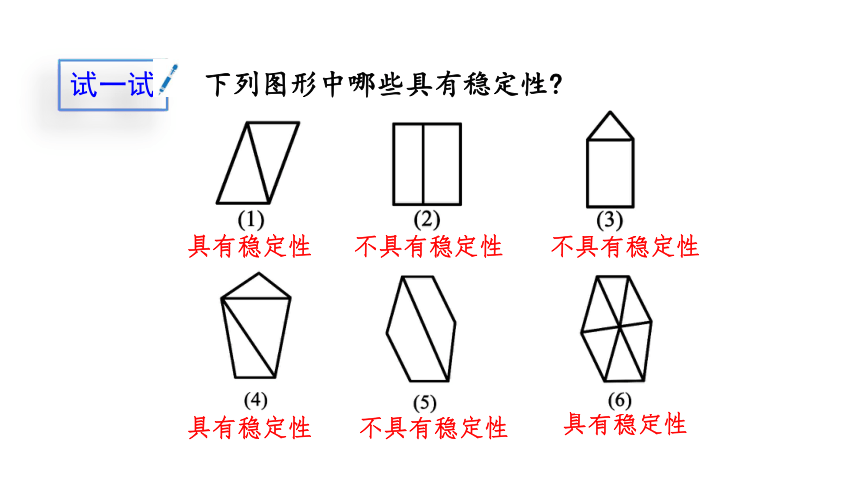
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
下列图形中哪些具有稳定性
试一试
四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
新知二 四边形不稳定性的应用
四边形的不稳定性有广泛的应用
活动晾衣架
伸缩门
遮阳棚
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗
四边形没有稳定性,怎样使它稳定呢
想一想
做一做
1. 牧民阿其木家用于圈羊的木栅门,由于年久失修已经变成如图甲,为什么会变形?
2. 为了恢复成原样图乙,而且要保持形状不变,他该怎么做呢?
(甲)
(乙)
帮帮忙
盖房子时,在窗框未安装好之前,工人师傅常常先在窗框上斜钉一根木条,为什么要这样做呢
三角形的稳定性
【思考】钉子架容易转动,怎样做可以使它稳定
例 要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使五边形,六边形木架,七边形木架保持稳定该怎么办呢
方法总结:为了使多边形具有稳定性,一般需要用木条将多边形固定成由一个一个的三角形组成的形式.
典例精析
1.下列图中具有稳定性有( )
A.1个 B.2个 C.3个 D.4个
C
课堂练习
2.下列关于三角形稳定性和四边形不稳定性的说 法正确的是( )
A.稳定性总是有益的,而不稳定性总是有害的
B.稳定性有利用价值,而不稳定性没有利用价值
C.稳定性和不稳定性均有利用价值
D.以上说法都不对
C
3. 如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短
B.三角形两边之和大于第三边
C.长方形的四个角都是直角
D.三角形的稳定性
D
B
A
E
F
C
D
应用
稳定性
三角形
独有性质
四边形具有不稳定性
归纳新知
1.如图,△ABC中,AC边上的高是( )
A.线段DA B.线段BA
C.线段BC D.线段BD
D
课后练习
2.以下是四位同学在钝角△ABC中画的BC边上的高,其中画法正确的是( )
B
3.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
4.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△ABC的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.DE是△BCD的中线
A
5.如图,BD是△ABC的中线,AD=2,AB+BC=5,则△ABC的周长为_____.
9
B
7.三角形的高、中线、角平分线都是( )
A.直线 B.线段
C.射线 D.以上情况都有
B
8.(2019·河北)下列图形具有稳定性的是( )
A
9.如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
D
10.若线段AP,AQ分别是△ABC边上的高和中线,则( )
A.AP>AQ B.AP≥AQ
C.AP<AQ D.AP≤AQ
11.下列说法中错误的是( )
A.三角形三条高至少有一条在三角形的内部
B.三角形三条中线都在三角形的内部
C.三角形三条角平分线都在三角形的内部
D.三角形三条高都在三角形的内部
D
D
12.用三角板作△ABC的边BC上的高时,下列三角板的摆放位置正确的是( )
A
13.如图,以AD为高的三角形共有____个.
6
14.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是_____.
9
15.(例题变式)如图,AD是△ABC的角平分线,DE∥AC交AB于点E,∠1=∠2,则DF与AB有什么关系?并说明理由.
解:DF∥AB.理由:∵DE∥AC,∴∠1=∠4,∵AD是△ABC的角平分线,∴∠3=∠4,∴∠1=∠3,又∵∠1=∠2,∴∠2=∠3,∴DF∥AB.
16.如图,在△ABC中,AB=AC,P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高,BD=8,求PF+PE的值.
17.如图,△ABC三边的中线AD,BE,CF的公共点为G,若S△ABC=12,求图中阴影部分的面积.
再 见
人教版数学 八年级上册
第十一章 三角形
11.1 与三角形有关的线段
11.1.3 三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗
想一想
导入新知
生活小常识
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,如图,为什么要这样做呢?
1. 了解三角形的稳定性和四边形的不稳定性.
2. 了解三角形的稳定性和四边形不稳定性的应用.
学习目标
动手做一做
1. 将三根木条用钉子钉成一个三角形木架.
2. 将四根木条用钉子钉成一个四边形木架.
新知一 三角形的稳定性
合作探究
请同学们看看:三角形和四边形的模型,扭一扭模型,它们的形状会改变吗
动动手
不会
会
1. 三角形具有稳定性.
2. 四边形没有稳定性.
理解“稳定性”
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
【思考】你能举出一些现实生活中应用三角形稳定性的例子吗
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
下列图形中哪些具有稳定性
试一试
四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
新知二 四边形不稳定性的应用
四边形的不稳定性有广泛的应用
活动晾衣架
伸缩门
遮阳棚
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗
四边形没有稳定性,怎样使它稳定呢
想一想
做一做
1. 牧民阿其木家用于圈羊的木栅门,由于年久失修已经变成如图甲,为什么会变形?
2. 为了恢复成原样图乙,而且要保持形状不变,他该怎么做呢?
(甲)
(乙)
帮帮忙
盖房子时,在窗框未安装好之前,工人师傅常常先在窗框上斜钉一根木条,为什么要这样做呢
三角形的稳定性
【思考】钉子架容易转动,怎样做可以使它稳定
例 要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使五边形,六边形木架,七边形木架保持稳定该怎么办呢
方法总结:为了使多边形具有稳定性,一般需要用木条将多边形固定成由一个一个的三角形组成的形式.
典例精析
1.下列图中具有稳定性有( )
A.1个 B.2个 C.3个 D.4个
C
课堂练习
2.下列关于三角形稳定性和四边形不稳定性的说 法正确的是( )
A.稳定性总是有益的,而不稳定性总是有害的
B.稳定性有利用价值,而不稳定性没有利用价值
C.稳定性和不稳定性均有利用价值
D.以上说法都不对
C
3. 如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短
B.三角形两边之和大于第三边
C.长方形的四个角都是直角
D.三角形的稳定性
D
B
A
E
F
C
D
应用
稳定性
三角形
独有性质
四边形具有不稳定性
归纳新知
1.如图,△ABC中,AC边上的高是( )
A.线段DA B.线段BA
C.线段BC D.线段BD
D
课后练习
2.以下是四位同学在钝角△ABC中画的BC边上的高,其中画法正确的是( )
B
3.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
4.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△ABC的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.DE是△BCD的中线
A
5.如图,BD是△ABC的中线,AD=2,AB+BC=5,则△ABC的周长为_____.
9
B
7.三角形的高、中线、角平分线都是( )
A.直线 B.线段
C.射线 D.以上情况都有
B
8.(2019·河北)下列图形具有稳定性的是( )
A
9.如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
D
10.若线段AP,AQ分别是△ABC边上的高和中线,则( )
A.AP>AQ B.AP≥AQ
C.AP<AQ D.AP≤AQ
11.下列说法中错误的是( )
A.三角形三条高至少有一条在三角形的内部
B.三角形三条中线都在三角形的内部
C.三角形三条角平分线都在三角形的内部
D.三角形三条高都在三角形的内部
D
D
12.用三角板作△ABC的边BC上的高时,下列三角板的摆放位置正确的是( )
A
13.如图,以AD为高的三角形共有____个.
6
14.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是_____.
9
15.(例题变式)如图,AD是△ABC的角平分线,DE∥AC交AB于点E,∠1=∠2,则DF与AB有什么关系?并说明理由.
解:DF∥AB.理由:∵DE∥AC,∴∠1=∠4,∵AD是△ABC的角平分线,∴∠3=∠4,∴∠1=∠3,又∵∠1=∠2,∴∠2=∠3,∴DF∥AB.
16.如图,在△ABC中,AB=AC,P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高,BD=8,求PF+PE的值.
17.如图,△ABC三边的中线AD,BE,CF的公共点为G,若S△ABC=12,求图中阴影部分的面积.
再 见
