鲁教版(五四学制)七年级上册 4.1无理数(共18张)
文档属性
| 名称 | 鲁教版(五四学制)七年级上册 4.1无理数(共18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 766.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 01:13:15 | ||
图片预览





文档简介
(共18张PPT)
4.1 无理数
学习目标
1.理解无理数的概念,会判断一个数是有理数还是
无理数.
2.能在数轴上表示某些简单的无理数.
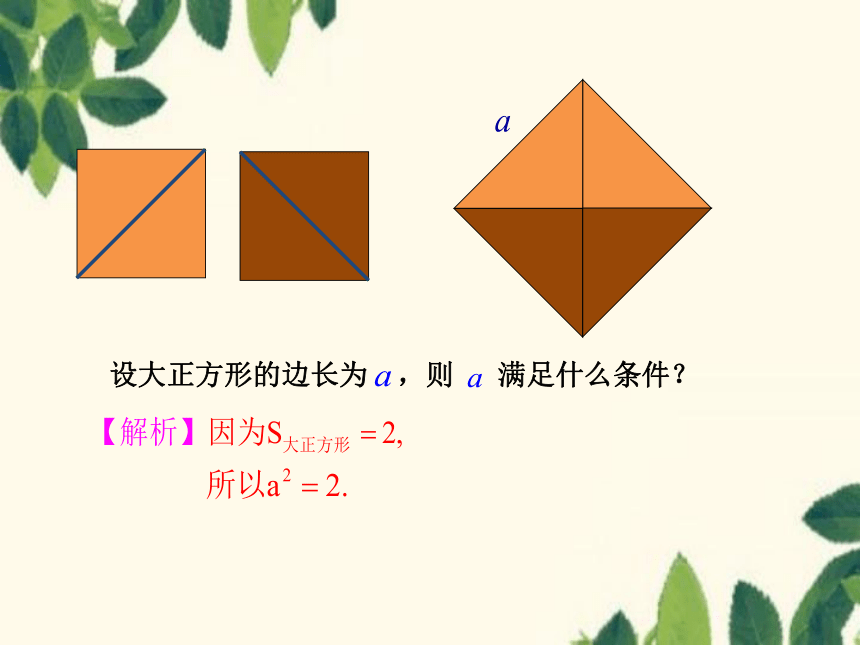
把两个边长为1的小正方形拼成一个大正方形
新课导入
设大正方形的边长为 ,则 满足什么条件?
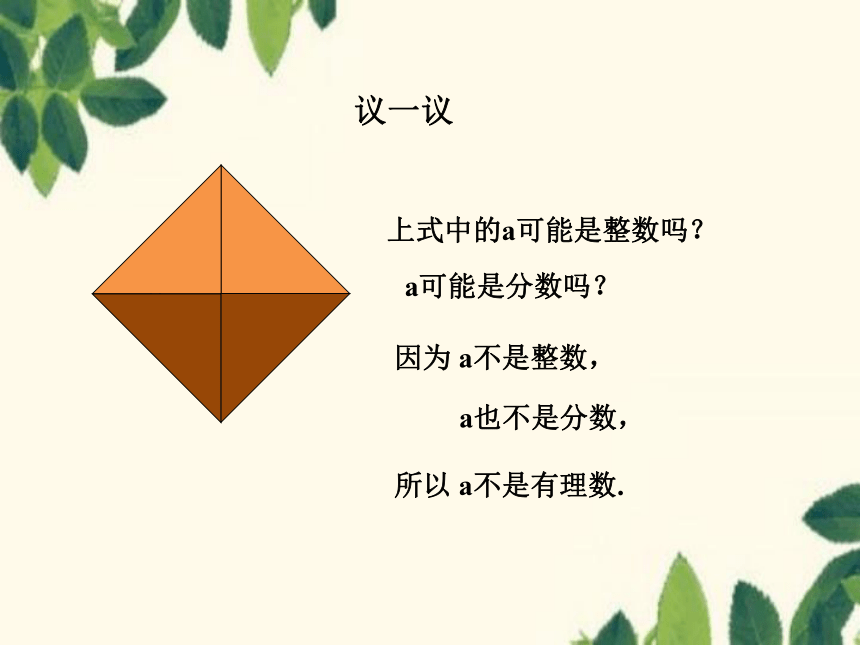
上式中的a可能是整数吗?
a可能是分数吗?
因为 a不是整数,
a也不是分数,
所以 a不是有理数.
议一议
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
探索发现
知识讲解
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环小数称为无理数.
0.101 001 000 1…(两个1之间依次多1个0)
-168.323 223 222 3…(两个3之间依次多1个2)
无理数的定义:
1
1
a
a
2
2
面积为2
由上可得边长a的一个大致的范围,但a的整数部分是几?十分位是几?百分位呢?千分位呢?……
估一估
请同学们借助计算器进行探索
边长a 面积S
11.41.411.4141.414 2算一算
11.961.988 11.999 3961.999 961 64边长a会不会算到某一位时,它的平方恰好等于2呢?为什么?
a可能是有限小数吗?它会是一个怎样的数呢?
事实上,a=1.414 213 56…,
它是一个无限不循环小数!
【例】把下列各数分别填入相应的有理数集合与无理数集合内:
(相邻两个3之间的7的个数逐次加1)
【例题】
有理数集合
无理数集合
(相邻两个3之间的7的个数逐次加1)
整数有_________________________________
有理数有_______________________________
无理数有_______________________________
实数有_________________________________
填空:在实数
【跟踪训练】
1.圆周率 及一些最终结果含有 的数.
2.开方开不尽的数.
3.有一定的规律,但不循环的无限小数.
无理数的特征:
【规律方法】
1.下列各数: (相邻两个3之间0
的个数逐次加1),1中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
【解析】选A.无限不循环小数是无理数,其中
(相邻两个3之间0的个数逐次加1)两个是无理数,其他是有理数.
随堂练习
2.下列各数中,是无理数的为( )
A. 3.14 B. C. D.
【解析】选C.因为3.14是小数, 是分数, 是无限循环小
数,所以选项A,B,D都是有理数; 是无
限不循环小数,所以是无理数.
通过本课时的学习,需要我们掌握:
无理数的概念:无限不循环小数称为无理数.
课堂小结
4.1 无理数
学习目标
1.理解无理数的概念,会判断一个数是有理数还是
无理数.
2.能在数轴上表示某些简单的无理数.
把两个边长为1的小正方形拼成一个大正方形
新课导入
设大正方形的边长为 ,则 满足什么条件?
上式中的a可能是整数吗?
a可能是分数吗?
因为 a不是整数,
a也不是分数,
所以 a不是有理数.
议一议
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
探索发现
知识讲解
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环小数称为无理数.
0.101 001 000 1…(两个1之间依次多1个0)
-168.323 223 222 3…(两个3之间依次多1个2)
无理数的定义:
1
1
a
a
2
2
面积为2
由上可得边长a的一个大致的范围,但a的整数部分是几?十分位是几?百分位呢?千分位呢?……
估一估
请同学们借助计算器进行探索
边长a 面积S
1
1
a可能是有限小数吗?它会是一个怎样的数呢?
事实上,a=1.414 213 56…,
它是一个无限不循环小数!
【例】把下列各数分别填入相应的有理数集合与无理数集合内:
(相邻两个3之间的7的个数逐次加1)
【例题】
有理数集合
无理数集合
(相邻两个3之间的7的个数逐次加1)
整数有_________________________________
有理数有_______________________________
无理数有_______________________________
实数有_________________________________
填空:在实数
【跟踪训练】
1.圆周率 及一些最终结果含有 的数.
2.开方开不尽的数.
3.有一定的规律,但不循环的无限小数.
无理数的特征:
【规律方法】
1.下列各数: (相邻两个3之间0
的个数逐次加1),1中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
【解析】选A.无限不循环小数是无理数,其中
(相邻两个3之间0的个数逐次加1)两个是无理数,其他是有理数.
随堂练习
2.下列各数中,是无理数的为( )
A. 3.14 B. C. D.
【解析】选C.因为3.14是小数, 是分数, 是无限循环小
数,所以选项A,B,D都是有理数; 是无
限不循环小数,所以是无理数.
通过本课时的学习,需要我们掌握:
无理数的概念:无限不循环小数称为无理数.
课堂小结
