2021-2022学年湘教版数学九年级下册期末达标检测卷(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级下册期末达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 526.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 08:37:26 | ||
图片预览

文档简介
期末达标检测卷
一、选择题(每题3分,共30分)
1.如图是一个放置在水平桌面上的锥形瓶,则它的俯视图为( )
2.【教材P125动脑筋变式】小玲参加综合知识竞赛活动,现有语文题6道、数学题5道、综合题9道,她从中随机抽取1道,抽中数学题的概率是( )
A. B. C. D.
3.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别为( )
A.0,5 B.0,1 C.-4,5 D.-4,1
4.如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D,连接OC.若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
5.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2
C.y3>y2>y1 D.y3>y1>y2
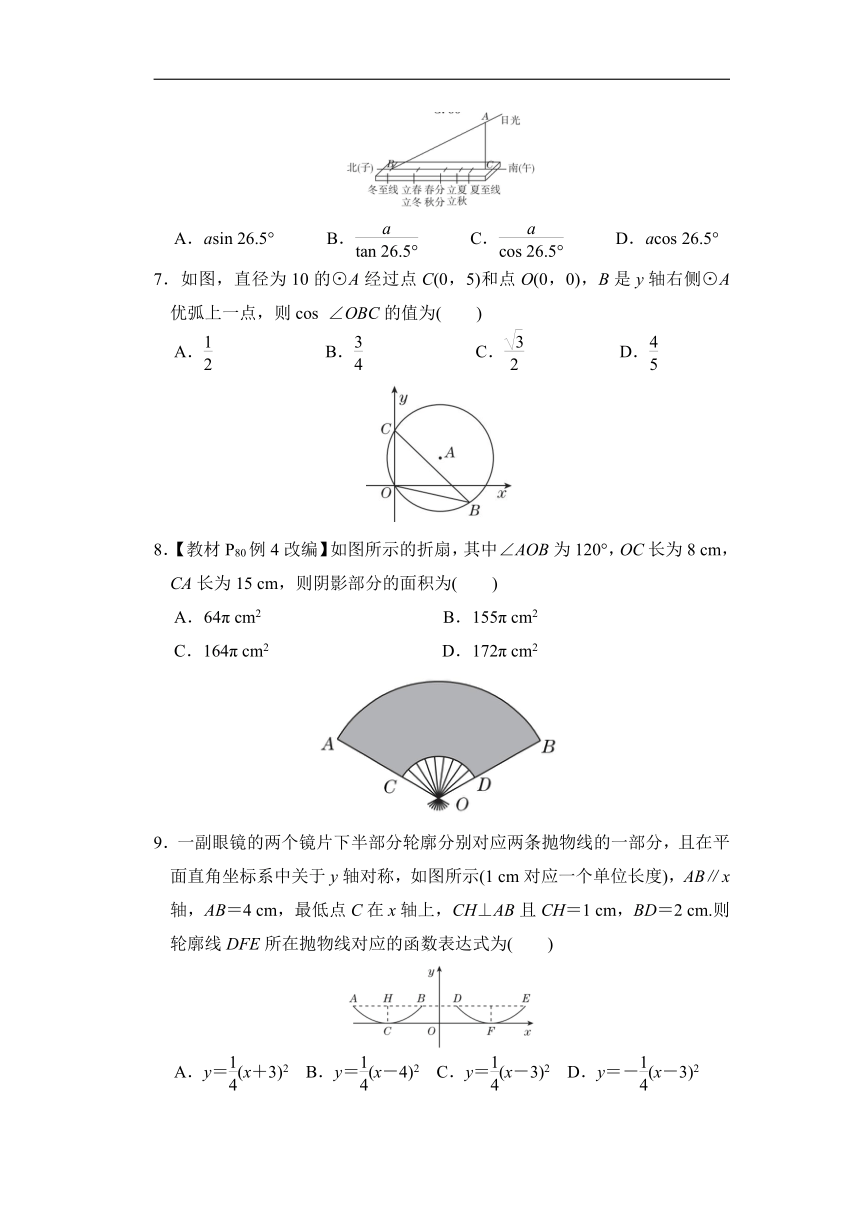
6.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A.asin 26.5° B. C. D.acos 26.5°
7.如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos ∠OBC的值为( )
A. B. C. D.
8.【教材P80例4改编】如图所示的折扇,其中∠AOB为120°,OC长为8 cm,CA长为15 cm,则阴影部分的面积为( )
A.64π cm2 B.155π cm2
C.164π cm2 D.172π cm2
9.一副眼镜的两个镜片下半部分轮廓分别对应两条抛物线的一部分,且在平面直角坐标系中关于y轴对称,如图所示(1 cm对应一个单位长度),AB∥x轴,AB=4 cm,最低点C在x轴上,CH⊥AB且CH=1 cm,BD=2 cm.则轮廓线DFE所在抛物线对应的函数表达式为( )
A.y=(x+3)2 B.y=(x-4)2 C.y=(x-3)2 D.y=-(x-3)2
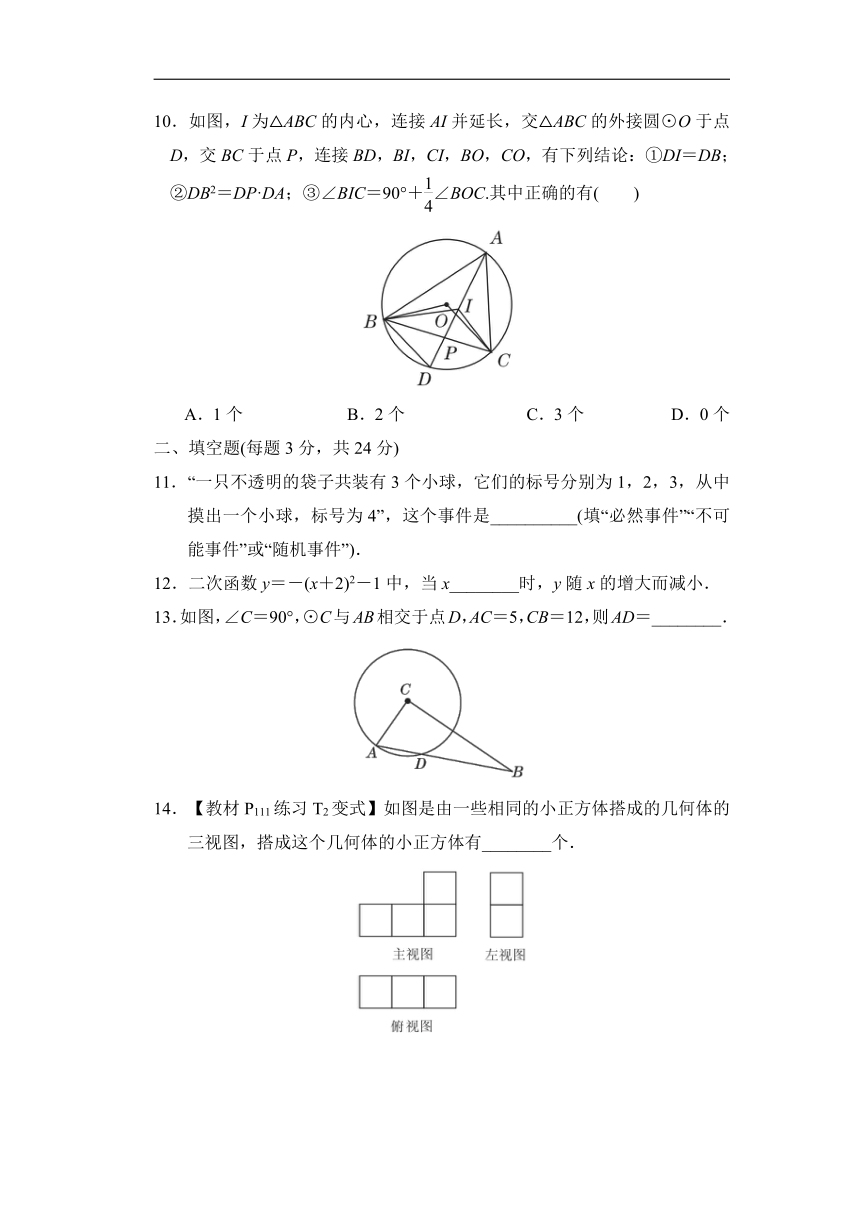
10.如图,I为△ABC的内心,连接AI并延长,交△ABC的外接圆⊙O于点D,交BC于点P,连接BD,BI,CI,BO,CO,有下列结论:①DI=DB;②DB2=DP·DA;③∠BIC=90°+∠BOC.其中正确的有( )
A.1个 B.2个 C.3个 D.0个
二、填空题(每题3分,共24分)
11.“一只不透明的袋子共装有3个小球,它们的标号分别为1,2,3,从中摸出一个小球,标号为4”,这个事件是__________(填“必然事件”“不可能事件”或“随机事件”).
12.二次函数y=-(x+2)2-1中,当x________时,y随x的增大而减小.
13.如图,∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,则AD=________.
14.【教材P111练习T2变式】如图是由一些相同的小正方体搭成的几何体的三视图,搭成这个几何体的小正方体有________个.
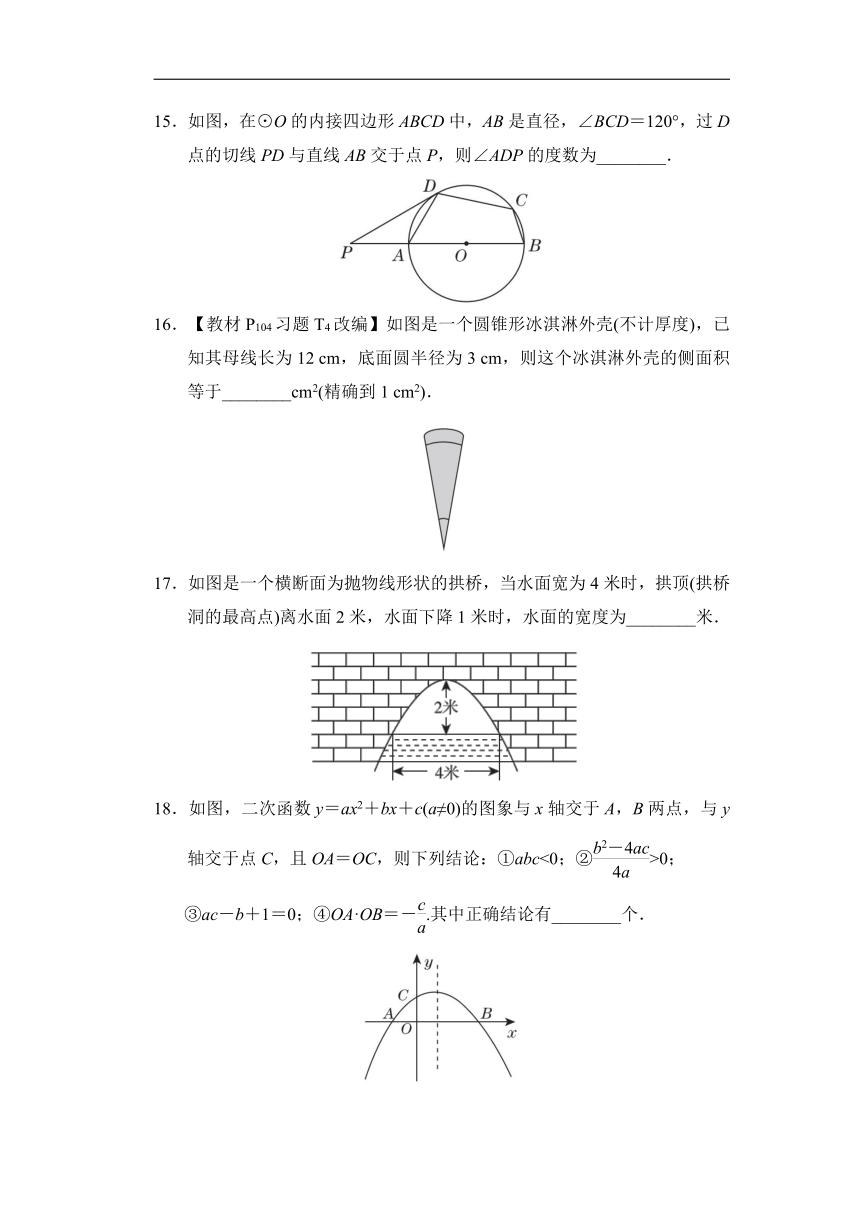
15.如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为________.
16.【教材P104习题T4改编】如图是一个圆锥形冰淇淋外壳(不计厚度),已知其母线长为12 cm,底面圆半径为3 cm,则这个冰淇淋外壳的侧面积等于________cm2(精确到1 cm2).
17.如图是一个横断面为抛物线形状的拱桥,当水面宽为4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为________米.
18.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②>0;
③ac-b+1=0;④OA·OB=-.其中正确结论有________个.
三、解答题(19~21题每题10分,其余每题12分,共66分)
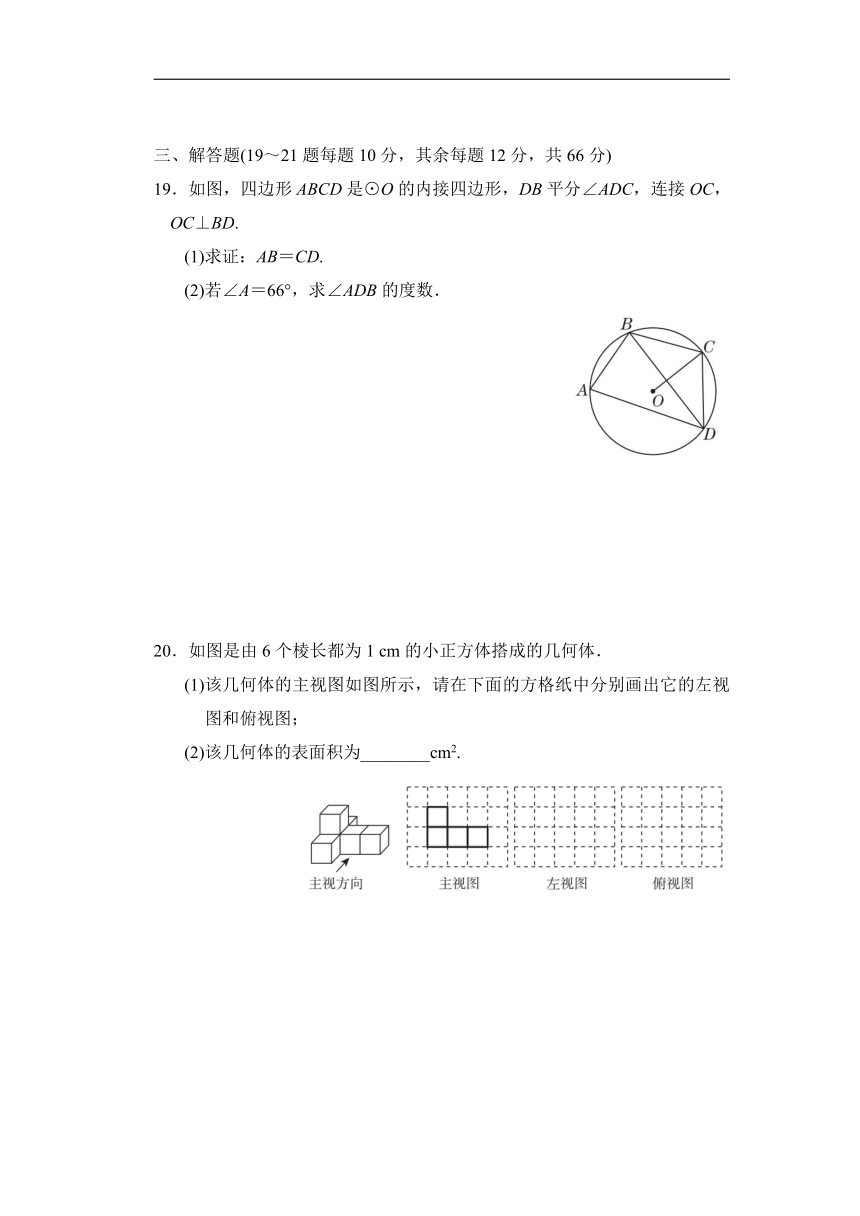
19.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A=66°,求∠ADB的度数.
20.如图是由6个棱长都为1 cm的小正方体搭成的几何体.
(1)该几何体的主视图如图所示,请在下面的方格纸中分别画出它的左视图和俯视图;
(2)该几何体的表面积为________cm2.
21.现有A,B两个不透明的袋子,分别装有3个除颜色外其他完全相同的小球.其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球.
(1)将A袋摇匀,然后从中随机摸出一个小球,求摸出白球的概率.
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两个袋子中各随机摸出一个小球,摸出的这两个小球若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.
22.一家服装店销售一种进价为50元/件的衬衣,生产厂家规定每件衬衣售价在60元至150元之间,当售价为60元/件时,每星期可卖出70件,该服装店老板调查发现,若每件每涨价10元,则每星期少卖出5件.
(1)当每件衬衣售价为多少元时(售价为10元的正整数倍),服装店每星期的利润最大?最大利润为多少元?
(2)请分析每件衬衣的售价定在什么范围内时,每星期的销售利润不低于
2 700元.
23.如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,点E是AC的中点,OE交CD于点F,连接DE.
(1)若∠BCD=36°,BC=10,求的长.
(2)判断直线DE与⊙O的位置关系,并说明理由.
(3)求证:2CE2=AB·EF.
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为,且与y轴交于点C(0,2),与x轴交于A,B两点.且点A在点B的左边.
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由.
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
答案
一、1.B 2.C 3.D 4.B 5.A 6.B
7.C 点拨:连接CA并延长,与圆相交于点D,易知点D是⊙A与x轴的另一交点,再利用同弧所对的圆周角相等得到∠OBC=∠ODC.在直角三角形OCD中,已知CD及OC的长,利用勾股定理可求出OD的长,然后利用余弦函数定义求出cos ∠ODC的值,即为cos ∠OBC的值.
8.B 9.C
10.C 点拨:∵I为△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠BID=∠BAD+∠ABI,∠DBI=∠DBC+∠CBI,∠CAD=∠DBC,∴∠DBI=∠DIB.
∴DI=DB.故①正确.
又易知△DBP∽△DAB,∴=,
∴DB2=DP·DA,故②正确.
∵∠BIC+∠IBC+∠ICB
=∠BIC+(∠ABC+∠ACB)
=∠BIC+(180°-∠BAC)
=∠BIC+90°-∠BAC=180°,
∴∠BIC=90°+∠BAC.
又∵∠BOC=2∠BAC,
∴∠BIC=90°+∠BOC,故③正确.
二、11.不可能事件 12.>-2 13. 14.4 15.30° 16.113
17.2 点拨:建立如图所示的平面直角坐标系,则抛物线顶点C的坐标为(0,2).设抛物线的表达式为y=ax2+2,则A(-2,0),B(2,0),代入得a=-,故y=-x2+2.当y=-1时,x=±.故水面的宽度为2米.
18.3 点拨:∵抛物线开口向下,∴a<0.
∵抛物线的对称轴在y轴的右侧,
∴->0,∴b>0.
∵抛物线与y轴的交点在x轴的上方,
∴c>0,∴abc<0.∴①正确.
∵抛物线与x轴有两个交点,
∴Δ=b2-4ac>0.而a<0,
∴<0.∴②错误.
易知点C的坐标为(0,c).
∵OA=OC,
∴点A的坐标为(-c,0).
把A(-c,0)的坐标代入y=ax2+bx+c得ac2-bc+c=0,∴c(ac-b+1)=0.
∵c≠0,∴ac-b+1=0.∴③正确.
设A(x1,0),B(x2,0),
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,∴x1·x2=,
∴OA·OB=-x1·x2=-.
∴④正确.
故正确的结论有3个.
三、 19.(1)证明:∵DB平分∠ADC,
∴=.
∵OC⊥BD,∴=,∴=,
∴AB=CD.
(2)解:∵四边形ABCD是⊙O的内接四边形,∴∠BCD=180°-∠A=114°.
∵=,∴BC=CD,
∴∠BDC=×(180°-114°)=33°.
∵DB平分∠ADC,
∴∠ADB=∠BDC=33°.
20.解:(1)如图.
(2)26
21.解:(1)从A袋随机摸出一个小球共有3种等可能的结果,而摸出白球的结果有2种,
∴P(摸出白球)=.
(2)根据题意,列表如下:
由表可知,共有9种等可能的结果,其中颜色不相同的结果有5种,颜色相同的结果有4种,
∴P(颜色不相同)=,P(颜色相同)=.
∵≠,即两人获胜的概率不相等,
∴这个游戏规则对双方不公平.
22.解:(1)设每件衬衣售价为x元,服装店每星期的利润为W元.
由题意得W=(x-50)=-x2+125x-5 000=-(x-125)2+2 812.5.
∵60≤x≤150,且x是10的正整数倍,
∴当x取120或130时,W有最大值2 800.
因此当每件衬衣售价为120元或130元时,服装店每星期的利润最大,最大利润为2 800元.
(2)由(1)知,销售利润W=-x2+125x-5 000,令W=2 700,
即-x2+125x-5 000=2 700,
解得x1=110,x2=140.
∴每件衬衣的售价定在110元至140元之间时(售价为10元的正整数倍),每星期的销售利润不低于2 700元.
23.(1)解:在⊙O中,∵BC=10,
∴OB=5.连接OD,
∵∠BCD=36°,∴∠BOD=72°,
∴的长为=2π.
(2)解:直线DE与⊙O相切.
理由:∵BC为⊙O的直径,
∴∠BDC=90°.
∵E是AC的中点,O是BC的中点,
∴OE为△ABC的中位线,∴OE∥AB,
∴∠OFC=90°.易知CF=FD,
∴OE垂直平分CD.∴CE=DE.
又∵OD=OC,OE=OE,
∴△ODE≌△OCE.
∴∠ODE=∠OCE.
∵∠ACB=90°,∴∠ODE=90°.
又∵OD为⊙O的半径,
∴直线DE与⊙O相切.
(3)证明:∵OE∥AB,∴∠A=∠OEC.
∵OE⊥CD,∴∠EFC=90°.
又∵∠ACB=90°,∴△ABC∽△ECF.
∴=.
∵E是AC的中点,∴2CE=AC.
∴2CE2=AB·EF.
24.解:(1)由题意可设抛物线的表达式为y=a(x-4)2-(a≠0).
∵抛物线经过点C(0,2),
∴a(0-4)2-=2,解得a=.
∴y=(x-4)2-,
即y=x2-x+2.
当y=0时,x2-x+2=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)存在.
易知抛物线的对称轴l为直线x=4,
A,B两点关于l对称.
连接CB交l于点P,
连接AP,则AP=BP,
∴AP+CP=BC,此时AP+CP的值最小.
∵B(6,0),C(0,2),∴OB=6,OC=2.
∴BC==2 .
∴AP+CP=BC=2 .
∴AP+CP的最小值为2 .
(3)连接ME.
∵CE是⊙M的切线,∴CE⊥ME.
∴∠CEM=90°.
∴∠COD=∠DEM=90°.
由题意,得OC=ME=2,∠ODC=∠MDE,
∴△COD≌△MED.
∴DC=DM.
易知OM=4.
设OD=x,
则CD=DM=OM-OD=4-x.
在Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2.∴x=.
∴D.
设直线CE的表达式为y=kx+d(k≠0),
∵直线CE过C(0,2),D两点,
则解得
∴直线CE的表达式为y=-x+2.
一、选择题(每题3分,共30分)
1.如图是一个放置在水平桌面上的锥形瓶,则它的俯视图为( )
2.【教材P125动脑筋变式】小玲参加综合知识竞赛活动,现有语文题6道、数学题5道、综合题9道,她从中随机抽取1道,抽中数学题的概率是( )
A. B. C. D.
3.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别为( )
A.0,5 B.0,1 C.-4,5 D.-4,1
4.如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D,连接OC.若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
5.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2
C.y3>y2>y1 D.y3>y1>y2
6.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A.asin 26.5° B. C. D.acos 26.5°
7.如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos ∠OBC的值为( )
A. B. C. D.
8.【教材P80例4改编】如图所示的折扇,其中∠AOB为120°,OC长为8 cm,CA长为15 cm,则阴影部分的面积为( )
A.64π cm2 B.155π cm2
C.164π cm2 D.172π cm2
9.一副眼镜的两个镜片下半部分轮廓分别对应两条抛物线的一部分,且在平面直角坐标系中关于y轴对称,如图所示(1 cm对应一个单位长度),AB∥x轴,AB=4 cm,最低点C在x轴上,CH⊥AB且CH=1 cm,BD=2 cm.则轮廓线DFE所在抛物线对应的函数表达式为( )
A.y=(x+3)2 B.y=(x-4)2 C.y=(x-3)2 D.y=-(x-3)2
10.如图,I为△ABC的内心,连接AI并延长,交△ABC的外接圆⊙O于点D,交BC于点P,连接BD,BI,CI,BO,CO,有下列结论:①DI=DB;②DB2=DP·DA;③∠BIC=90°+∠BOC.其中正确的有( )
A.1个 B.2个 C.3个 D.0个
二、填空题(每题3分,共24分)
11.“一只不透明的袋子共装有3个小球,它们的标号分别为1,2,3,从中摸出一个小球,标号为4”,这个事件是__________(填“必然事件”“不可能事件”或“随机事件”).
12.二次函数y=-(x+2)2-1中,当x________时,y随x的增大而减小.
13.如图,∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,则AD=________.
14.【教材P111练习T2变式】如图是由一些相同的小正方体搭成的几何体的三视图,搭成这个几何体的小正方体有________个.
15.如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为________.
16.【教材P104习题T4改编】如图是一个圆锥形冰淇淋外壳(不计厚度),已知其母线长为12 cm,底面圆半径为3 cm,则这个冰淇淋外壳的侧面积等于________cm2(精确到1 cm2).
17.如图是一个横断面为抛物线形状的拱桥,当水面宽为4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为________米.
18.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②>0;
③ac-b+1=0;④OA·OB=-.其中正确结论有________个.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A=66°,求∠ADB的度数.
20.如图是由6个棱长都为1 cm的小正方体搭成的几何体.
(1)该几何体的主视图如图所示,请在下面的方格纸中分别画出它的左视图和俯视图;
(2)该几何体的表面积为________cm2.
21.现有A,B两个不透明的袋子,分别装有3个除颜色外其他完全相同的小球.其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球.
(1)将A袋摇匀,然后从中随机摸出一个小球,求摸出白球的概率.
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两个袋子中各随机摸出一个小球,摸出的这两个小球若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.
22.一家服装店销售一种进价为50元/件的衬衣,生产厂家规定每件衬衣售价在60元至150元之间,当售价为60元/件时,每星期可卖出70件,该服装店老板调查发现,若每件每涨价10元,则每星期少卖出5件.
(1)当每件衬衣售价为多少元时(售价为10元的正整数倍),服装店每星期的利润最大?最大利润为多少元?
(2)请分析每件衬衣的售价定在什么范围内时,每星期的销售利润不低于
2 700元.
23.如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,点E是AC的中点,OE交CD于点F,连接DE.
(1)若∠BCD=36°,BC=10,求的长.
(2)判断直线DE与⊙O的位置关系,并说明理由.
(3)求证:2CE2=AB·EF.
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为,且与y轴交于点C(0,2),与x轴交于A,B两点.且点A在点B的左边.
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由.
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
答案
一、1.B 2.C 3.D 4.B 5.A 6.B
7.C 点拨:连接CA并延长,与圆相交于点D,易知点D是⊙A与x轴的另一交点,再利用同弧所对的圆周角相等得到∠OBC=∠ODC.在直角三角形OCD中,已知CD及OC的长,利用勾股定理可求出OD的长,然后利用余弦函数定义求出cos ∠ODC的值,即为cos ∠OBC的值.
8.B 9.C
10.C 点拨:∵I为△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠BID=∠BAD+∠ABI,∠DBI=∠DBC+∠CBI,∠CAD=∠DBC,∴∠DBI=∠DIB.
∴DI=DB.故①正确.
又易知△DBP∽△DAB,∴=,
∴DB2=DP·DA,故②正确.
∵∠BIC+∠IBC+∠ICB
=∠BIC+(∠ABC+∠ACB)
=∠BIC+(180°-∠BAC)
=∠BIC+90°-∠BAC=180°,
∴∠BIC=90°+∠BAC.
又∵∠BOC=2∠BAC,
∴∠BIC=90°+∠BOC,故③正确.
二、11.不可能事件 12.>-2 13. 14.4 15.30° 16.113
17.2 点拨:建立如图所示的平面直角坐标系,则抛物线顶点C的坐标为(0,2).设抛物线的表达式为y=ax2+2,则A(-2,0),B(2,0),代入得a=-,故y=-x2+2.当y=-1时,x=±.故水面的宽度为2米.
18.3 点拨:∵抛物线开口向下,∴a<0.
∵抛物线的对称轴在y轴的右侧,
∴->0,∴b>0.
∵抛物线与y轴的交点在x轴的上方,
∴c>0,∴abc<0.∴①正确.
∵抛物线与x轴有两个交点,
∴Δ=b2-4ac>0.而a<0,
∴<0.∴②错误.
易知点C的坐标为(0,c).
∵OA=OC,
∴点A的坐标为(-c,0).
把A(-c,0)的坐标代入y=ax2+bx+c得ac2-bc+c=0,∴c(ac-b+1)=0.
∵c≠0,∴ac-b+1=0.∴③正确.
设A(x1,0),B(x2,0),
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,∴x1·x2=,
∴OA·OB=-x1·x2=-.
∴④正确.
故正确的结论有3个.
三、 19.(1)证明:∵DB平分∠ADC,
∴=.
∵OC⊥BD,∴=,∴=,
∴AB=CD.
(2)解:∵四边形ABCD是⊙O的内接四边形,∴∠BCD=180°-∠A=114°.
∵=,∴BC=CD,
∴∠BDC=×(180°-114°)=33°.
∵DB平分∠ADC,
∴∠ADB=∠BDC=33°.
20.解:(1)如图.
(2)26
21.解:(1)从A袋随机摸出一个小球共有3种等可能的结果,而摸出白球的结果有2种,
∴P(摸出白球)=.
(2)根据题意,列表如下:
由表可知,共有9种等可能的结果,其中颜色不相同的结果有5种,颜色相同的结果有4种,
∴P(颜色不相同)=,P(颜色相同)=.
∵≠,即两人获胜的概率不相等,
∴这个游戏规则对双方不公平.
22.解:(1)设每件衬衣售价为x元,服装店每星期的利润为W元.
由题意得W=(x-50)=-x2+125x-5 000=-(x-125)2+2 812.5.
∵60≤x≤150,且x是10的正整数倍,
∴当x取120或130时,W有最大值2 800.
因此当每件衬衣售价为120元或130元时,服装店每星期的利润最大,最大利润为2 800元.
(2)由(1)知,销售利润W=-x2+125x-5 000,令W=2 700,
即-x2+125x-5 000=2 700,
解得x1=110,x2=140.
∴每件衬衣的售价定在110元至140元之间时(售价为10元的正整数倍),每星期的销售利润不低于2 700元.
23.(1)解:在⊙O中,∵BC=10,
∴OB=5.连接OD,
∵∠BCD=36°,∴∠BOD=72°,
∴的长为=2π.
(2)解:直线DE与⊙O相切.
理由:∵BC为⊙O的直径,
∴∠BDC=90°.
∵E是AC的中点,O是BC的中点,
∴OE为△ABC的中位线,∴OE∥AB,
∴∠OFC=90°.易知CF=FD,
∴OE垂直平分CD.∴CE=DE.
又∵OD=OC,OE=OE,
∴△ODE≌△OCE.
∴∠ODE=∠OCE.
∵∠ACB=90°,∴∠ODE=90°.
又∵OD为⊙O的半径,
∴直线DE与⊙O相切.
(3)证明:∵OE∥AB,∴∠A=∠OEC.
∵OE⊥CD,∴∠EFC=90°.
又∵∠ACB=90°,∴△ABC∽△ECF.
∴=.
∵E是AC的中点,∴2CE=AC.
∴2CE2=AB·EF.
24.解:(1)由题意可设抛物线的表达式为y=a(x-4)2-(a≠0).
∵抛物线经过点C(0,2),
∴a(0-4)2-=2,解得a=.
∴y=(x-4)2-,
即y=x2-x+2.
当y=0时,x2-x+2=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)存在.
易知抛物线的对称轴l为直线x=4,
A,B两点关于l对称.
连接CB交l于点P,
连接AP,则AP=BP,
∴AP+CP=BC,此时AP+CP的值最小.
∵B(6,0),C(0,2),∴OB=6,OC=2.
∴BC==2 .
∴AP+CP=BC=2 .
∴AP+CP的最小值为2 .
(3)连接ME.
∵CE是⊙M的切线,∴CE⊥ME.
∴∠CEM=90°.
∴∠COD=∠DEM=90°.
由题意,得OC=ME=2,∠ODC=∠MDE,
∴△COD≌△MED.
∴DC=DM.
易知OM=4.
设OD=x,
则CD=DM=OM-OD=4-x.
在Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2.∴x=.
∴D.
设直线CE的表达式为y=kx+d(k≠0),
∵直线CE过C(0,2),D两点,
则解得
∴直线CE的表达式为y=-x+2.
同课章节目录
