勾股定理的应用
图片预览




文档简介
(共18张PPT)
勾股定理能解决直角三角形中的许多问题,因此在我们的现实生活中有着广泛的应用,本节课我们将学习它在实际生活中应用。
实例:两军舰同时从某军港O出发执行任务,甲舰以30海里/时的速度向西北方向航行,乙舰以40海里/时的速度向西南方向航行,1小时后两舰相距多远?
①请同学们想一想:解决实际问题的关键是什么?
②请学生们再动动脑筋,能不能找出勾股定理在现实生活中运用的实例呢?
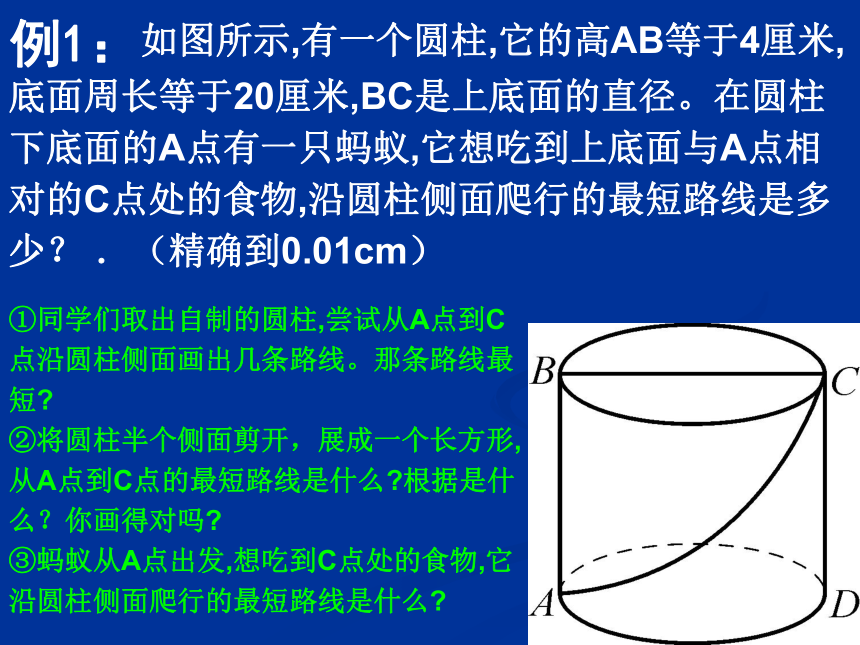
例1:如图所示,有一个圆柱,它的高AB等于4厘米,底面周长等于20厘米,BC是上底面的直径。在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的C点处的食物,沿圆柱侧面爬行的最短路线是多少? .(精确到0.01cm)
①同学们取出自制的圆柱,尝试从A点到C点沿圆柱侧面画出几条路线。那条路线最短
②将圆柱半个侧面剪开,展成一个长方形,从A点到C点的最短路线是什么 根据是什么?你画得对吗
③蚂蚁从A点出发,想吃到C点处的食物,它沿圆柱侧面爬行的最短路线是什么
B
A
cm
10cm
4cm
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开,得到矩形ABCD,根据“两点之间,线段最短”,所求的最短路线就是圆柱半个侧面展开图即矩形对角线AC之长。
解:在Rt△ABC中,BC=底面周长的一半=10cm,
(勾股定理)
答:最短路程约为10.77cm.
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
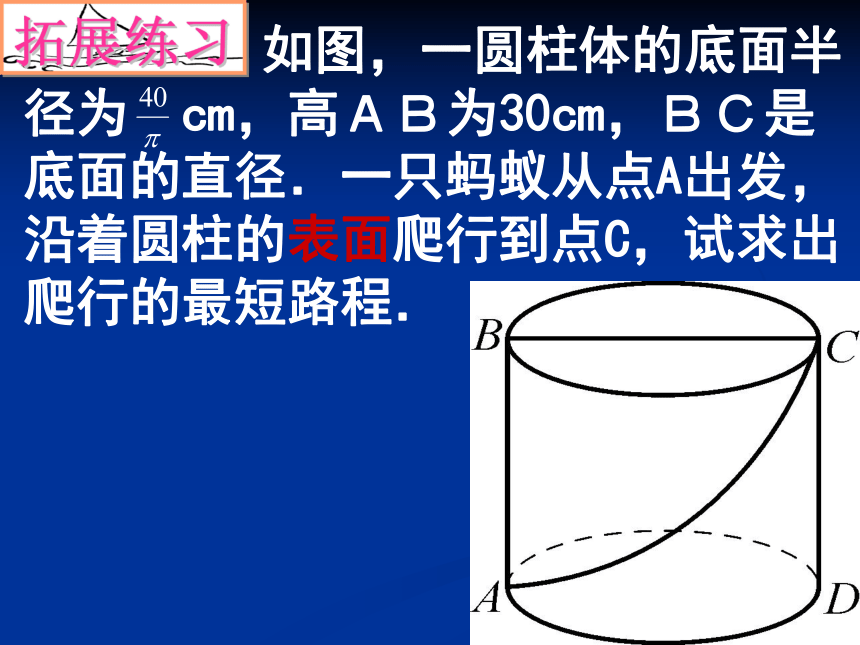
如图,一圆柱体的底面半径为 cm,高AB为30cm,BC是底面的直径.一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,试求出爬行的最短路程.
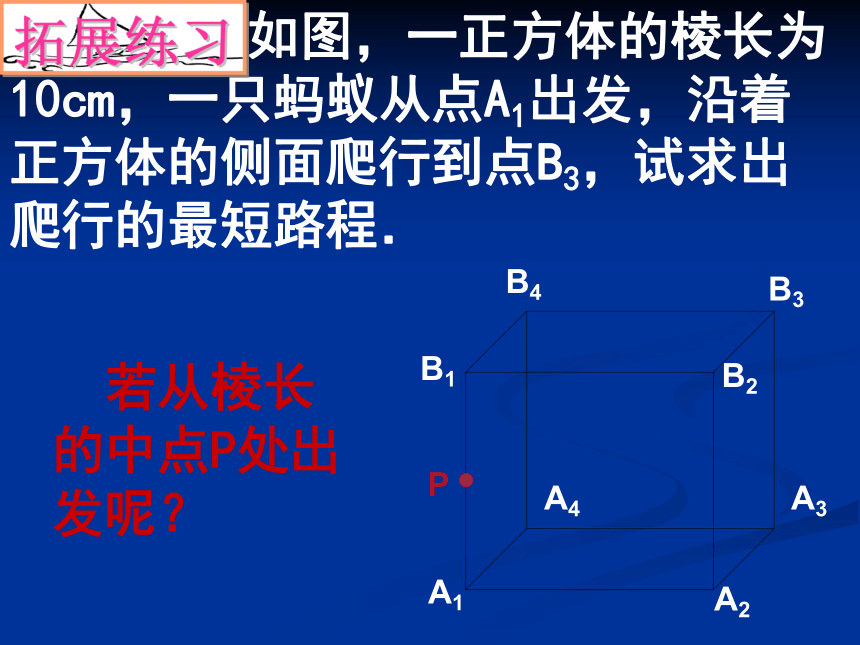
如图,一正方体的棱长为10cm,一只蚂蚁从点A1出发,沿着正方体的侧面爬行到点B3,试求出爬行的最短路程.
A1
A4
A3
A2
B1
B2
B3
B4
P
若从棱长的中点P处出发呢?
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如右图的某工厂,问这辆卡车能否通过该工厂的厂门
2.3米
2米
分析:如图由于厂门的宽度是足够的,这个问题的关键是观察当卡车位于厂门正中间时其高度是否小于CH,点D在离厂门中线0.8米处,CD⊥AB,与地面交于H,寻找出Rt△OCD,运用勾股定理求出CD。
解:在Rt△OCD中,由勾股定理得
因此高度上有0.4米的余量,所以卡车能通过厂门
试一试:
在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?
D
A
B
C
解:设,则水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1
=12+1
=13(米)
答:水池的深度为12米,芦苇高为13米.
想一想
小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电
视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉
得一定是售货员搞错了.你同意他的想法吗?你能解释这是
为什么吗?
1、勾股定理在生活中的应用非常广泛,那么,用勾股定理解题时的步骤是什么?
2、谈谈这节课你的收获,还存在哪些问题。
作业:
1、巩固练习
P58练习第1、2题
2、作业
P60 习题14.2第1、2 题
勾股定理能解决直角三角形中的许多问题,因此在我们的现实生活中有着广泛的应用,本节课我们将学习它在实际生活中应用。
实例:两军舰同时从某军港O出发执行任务,甲舰以30海里/时的速度向西北方向航行,乙舰以40海里/时的速度向西南方向航行,1小时后两舰相距多远?
①请同学们想一想:解决实际问题的关键是什么?
②请学生们再动动脑筋,能不能找出勾股定理在现实生活中运用的实例呢?
例1:如图所示,有一个圆柱,它的高AB等于4厘米,底面周长等于20厘米,BC是上底面的直径。在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的C点处的食物,沿圆柱侧面爬行的最短路线是多少? .(精确到0.01cm)
①同学们取出自制的圆柱,尝试从A点到C点沿圆柱侧面画出几条路线。那条路线最短
②将圆柱半个侧面剪开,展成一个长方形,从A点到C点的最短路线是什么 根据是什么?你画得对吗
③蚂蚁从A点出发,想吃到C点处的食物,它沿圆柱侧面爬行的最短路线是什么
B
A
cm
10cm
4cm
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开,得到矩形ABCD,根据“两点之间,线段最短”,所求的最短路线就是圆柱半个侧面展开图即矩形对角线AC之长。
解:在Rt△ABC中,BC=底面周长的一半=10cm,
(勾股定理)
答:最短路程约为10.77cm.
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
如图,一圆柱体的底面半径为 cm,高AB为30cm,BC是底面的直径.一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,试求出爬行的最短路程.
如图,一正方体的棱长为10cm,一只蚂蚁从点A1出发,沿着正方体的侧面爬行到点B3,试求出爬行的最短路程.
A1
A4
A3
A2
B1
B2
B3
B4
P
若从棱长的中点P处出发呢?
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如右图的某工厂,问这辆卡车能否通过该工厂的厂门
2.3米
2米
分析:如图由于厂门的宽度是足够的,这个问题的关键是观察当卡车位于厂门正中间时其高度是否小于CH,点D在离厂门中线0.8米处,CD⊥AB,与地面交于H,寻找出Rt△OCD,运用勾股定理求出CD。
解:在Rt△OCD中,由勾股定理得
因此高度上有0.4米的余量,所以卡车能通过厂门
试一试:
在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?
D
A
B
C
解:设,则水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1
=12+1
=13(米)
答:水池的深度为12米,芦苇高为13米.
想一想
小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电
视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉
得一定是售货员搞错了.你同意他的想法吗?你能解释这是
为什么吗?
1、勾股定理在生活中的应用非常广泛,那么,用勾股定理解题时的步骤是什么?
2、谈谈这节课你的收获,还存在哪些问题。
作业:
1、巩固练习
P58练习第1、2题
2、作业
P60 习题14.2第1、2 题
