平行四边形的复习课件
图片预览




文档简介
(共16张PPT)
第20章 平行四边形的判定
复习课
华东师范大学出版社
义务教育课程标准实验教科书 八年级数学(下)
我会构建
我会学习
我会听讲
我会动手
我会探索
我会变式
我会总结
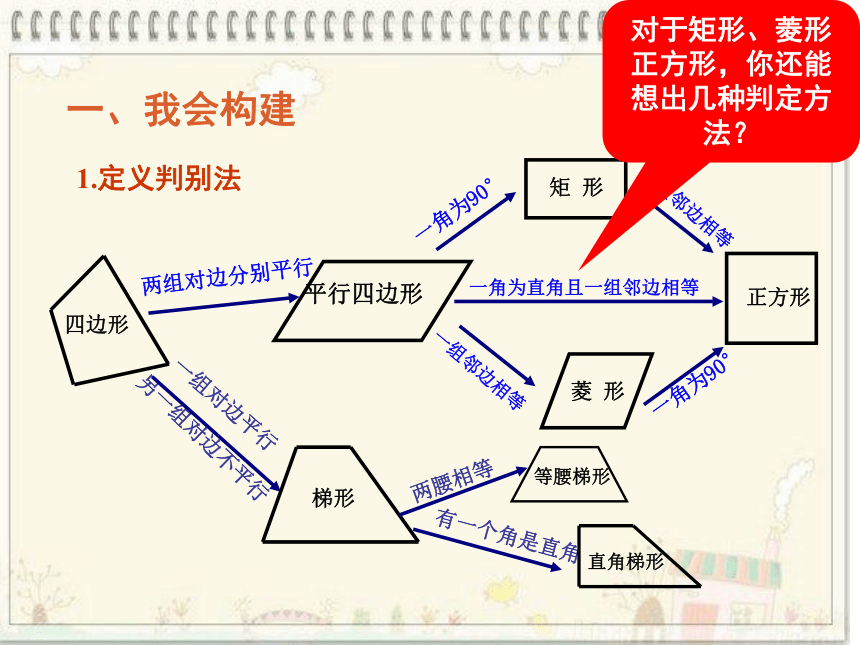
四边形
平行四边形
矩 形
菱 形
一角为90°
正方形
两组对边分别平行
一角为直角且一组邻边相等
一组邻边相等
一组邻边相等
一角为90°
一、我会构建
1.定义判别法
一组对边平行
另一组对边不平行
梯形
两腰相等
有一个角是直角
等腰梯形
直角梯形
对于矩形、菱形正方形,你还能想出几种判定方法?
梯形辅助线总结
A
B
C
D
E
F
A
B
C
D
E
A
B
C
D
O
2.
3.发散思维
4.整体梳理
平行四边形
矩形
菱形
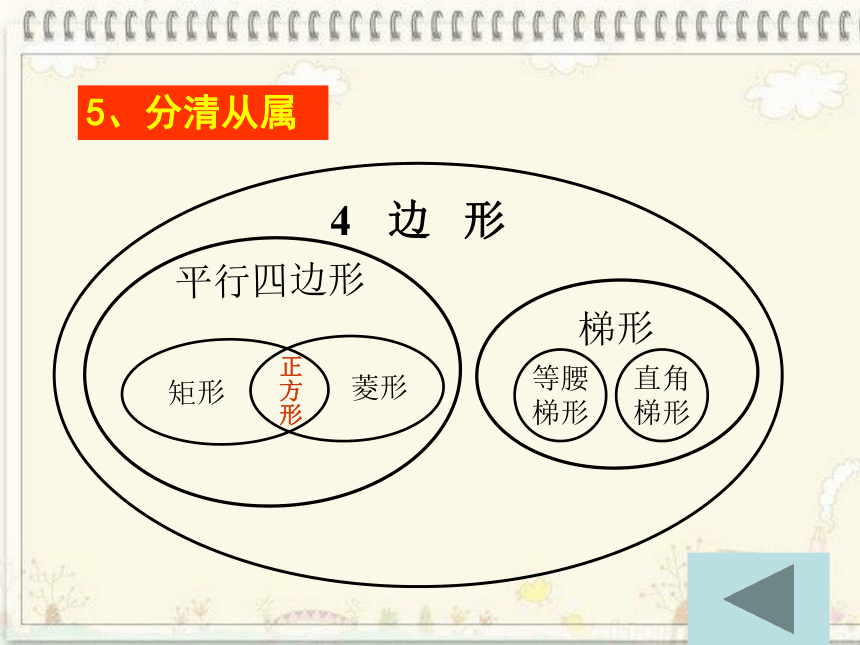
5、分清从属
边 形
梯形
等腰
梯形
直角
梯形
正方形
(2)若四边形ABCD为平行四边形,请补充条件
使得四边形ABCD为菱形.
(1)已知:AD∥BC,要使四边形ABCD为平行四边形,需要增加条件是___________________.
AB=BC、
或AD=BC、或∠A=∠C、或∠B=∠D 、
或∠A+∠D=180°、 或∠B+∠C=180°.
二.我会听讲
AC⊥BD
AB∥DC
火眼金睛:
AB=CD可以吗?
(3)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC, 若对角线 AC=6cm,则你能提出什么问题?
(4)如图,菱形ABCD的边长为8cm,∠BAD=120°,你会提什么问题?
A
B
C
D
O
我发现:
当矩形对角线夹角为60°时,以等边三角形为突破口;当菱形有一个内角为60°时,以等边三角形为突破口.
角?
边?
周长?
面积?
菱形的面积等于它的两条对角线乘积的一半.
我想到:
B
A
D
C
O
我也会提问
如:菱形的面积为多少?
(1)用直尺和圆规作正方形;
(2)把长方形的纸片通过折纸, 剪 出一个正方形纸片.
说说你作图和剪纸的理由.
三.我会动手
6.如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
A
B
D
C
O
P
解:四边形CODP是菱形
∵ DP∥OC, DP=OC,
∴ 四边形CODP是平行四边形.
∵四边形ABCD是矩形 ,
∴CO=DO.
∴四边形CODP是菱形 .
四、我会探索
如果题目中的矩形变为正方形(图二),结论又应变为什么?
如果题目中的矩形变为菱形(图一),结论应变为什么?
图一
A
O
D
P
B
C
P
C
D
O
B
A
图二
A
B
D
C
O
P
1) 如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
五、我会变式
变式1:
变式2:
①当∠BAC等于 时,四边形ADFE是矩形;
②当∠BAC等于 时,平行四边形ADFE不存在;
③当△ABC分别满足什么条件时,平行四边形是菱形、正方形.
(2)以△ABC的边AB、AC为边作等边△ABD和等边△ ACE,DF∥AE,EF ∥AD,
解: ③ AB=AC时,平行四边形ADFE时菱形.
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形.
150°
60°
B
C
A
E
F
D
60°
60°
实践出真知
演示
走近中招
如图,在梯形ABCD中,E是BC的中点,点P是边BC上一动点,设BP的长为
(1)当 的值为______时,以点P、A、D、E为顶点的四边形为直角梯形
(2)当 的值为_____时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC上运动过程中,以点P、A、D、E为顶点的四边形能否为菱形 试说明理由
A
B
C
D
P
E
从结论入手,例如: 若它为直角梯形,则能得出∠PAD或∠EPD为直角,
分析
演示
解题过程
解:(1)3或8
(2)1或11
(3)当x=11时,以A、P、E、D
为顶点的四边形是菱形。
证明:过点D作DH⊥BC,垂足为H。
∵∠C=45°,CD=
∴CH= DH= 4
∵PB=11,BC=12
∴CP=1,PH=CH-PC=4-1=3
在RT⊿DPH中,PD=
由(2)知,当x=PB=11时,它是平行四边形
∴以A、P、E、D为顶点的四边 形是菱形。
A
B
C
D
P
E
H
∟
六、我会总结
1.平行四边形及特殊平行四边形的判定方法
2.梯形及特殊梯形的判定方法
3.逆向思维的思考方法;
4.发散思维的思考方法.
还有……
七.布置作业:
课本124页 第1、5、7
第20章 平行四边形的判定
复习课
华东师范大学出版社
义务教育课程标准实验教科书 八年级数学(下)
我会构建
我会学习
我会听讲
我会动手
我会探索
我会变式
我会总结
四边形
平行四边形
矩 形
菱 形
一角为90°
正方形
两组对边分别平行
一角为直角且一组邻边相等
一组邻边相等
一组邻边相等
一角为90°
一、我会构建
1.定义判别法
一组对边平行
另一组对边不平行
梯形
两腰相等
有一个角是直角
等腰梯形
直角梯形
对于矩形、菱形正方形,你还能想出几种判定方法?
梯形辅助线总结
A
B
C
D
E
F
A
B
C
D
E
A
B
C
D
O
2.
3.发散思维
4.整体梳理
平行四边形
矩形
菱形
5、分清从属
边 形
梯形
等腰
梯形
直角
梯形
正方形
(2)若四边形ABCD为平行四边形,请补充条件
使得四边形ABCD为菱形.
(1)已知:AD∥BC,要使四边形ABCD为平行四边形,需要增加条件是___________________.
AB=BC、
或AD=BC、或∠A=∠C、或∠B=∠D 、
或∠A+∠D=180°、 或∠B+∠C=180°.
二.我会听讲
AC⊥BD
AB∥DC
火眼金睛:
AB=CD可以吗?
(3)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC, 若对角线 AC=6cm,则你能提出什么问题?
(4)如图,菱形ABCD的边长为8cm,∠BAD=120°,你会提什么问题?
A
B
C
D
O
我发现:
当矩形对角线夹角为60°时,以等边三角形为突破口;当菱形有一个内角为60°时,以等边三角形为突破口.
角?
边?
周长?
面积?
菱形的面积等于它的两条对角线乘积的一半.
我想到:
B
A
D
C
O
我也会提问
如:菱形的面积为多少?
(1)用直尺和圆规作正方形;
(2)把长方形的纸片通过折纸, 剪 出一个正方形纸片.
说说你作图和剪纸的理由.
三.我会动手
6.如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
A
B
D
C
O
P
解:四边形CODP是菱形
∵ DP∥OC, DP=OC,
∴ 四边形CODP是平行四边形.
∵四边形ABCD是矩形 ,
∴CO=DO.
∴四边形CODP是菱形 .
四、我会探索
如果题目中的矩形变为正方形(图二),结论又应变为什么?
如果题目中的矩形变为菱形(图一),结论应变为什么?
图一
A
O
D
P
B
C
P
C
D
O
B
A
图二
A
B
D
C
O
P
1) 如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
五、我会变式
变式1:
变式2:
①当∠BAC等于 时,四边形ADFE是矩形;
②当∠BAC等于 时,平行四边形ADFE不存在;
③当△ABC分别满足什么条件时,平行四边形是菱形、正方形.
(2)以△ABC的边AB、AC为边作等边△ABD和等边△ ACE,DF∥AE,EF ∥AD,
解: ③ AB=AC时,平行四边形ADFE时菱形.
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形.
150°
60°
B
C
A
E
F
D
60°
60°
实践出真知
演示
走近中招
如图,在梯形ABCD中,E是BC的中点,点P是边BC上一动点,设BP的长为
(1)当 的值为______时,以点P、A、D、E为顶点的四边形为直角梯形
(2)当 的值为_____时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC上运动过程中,以点P、A、D、E为顶点的四边形能否为菱形 试说明理由
A
B
C
D
P
E
从结论入手,例如: 若它为直角梯形,则能得出∠PAD或∠EPD为直角,
分析
演示
解题过程
解:(1)3或8
(2)1或11
(3)当x=11时,以A、P、E、D
为顶点的四边形是菱形。
证明:过点D作DH⊥BC,垂足为H。
∵∠C=45°,CD=
∴CH= DH= 4
∵PB=11,BC=12
∴CP=1,PH=CH-PC=4-1=3
在RT⊿DPH中,PD=
由(2)知,当x=PB=11时,它是平行四边形
∴以A、P、E、D为顶点的四边 形是菱形。
A
B
C
D
P
E
H
∟
六、我会总结
1.平行四边形及特殊平行四边形的判定方法
2.梯形及特殊梯形的判定方法
3.逆向思维的思考方法;
4.发散思维的思考方法.
还有……
七.布置作业:
课本124页 第1、5、7
