第二章点、直线、平面之间的位置关系达标检测-2021-2022学年高一上学期数学人教A版必修2(Word含解析)
文档属性
| 名称 | 第二章点、直线、平面之间的位置关系达标检测-2021-2022学年高一上学期数学人教A版必修2(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 399.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:57:42 | ||
图片预览




文档简介
本章达标检测
一、选择题(本题共12小题,每小题5分,共60分)
1.下列命题正确的是( )
①过平面外一点有且仅有一个平面与已知平面垂直;
②如果一条直线和两个垂直平面中的一个垂直,那么它必和另一个平面平行;
③过不在平面内的一条直线可作无数个平面与已知平面垂直;
④如果两个平面互相垂直,那么经过一个平面内一点与另一平面垂直的直线在第一个平面内.
A.①③ B.②③
C.②③④ D.④
2.平面α与平面β平行的条件可以是( )
A.α内有无数多条直线都与β平行
B.直线a α,b β,且a∥β,b∥α
C.直线a∥α,a∥β,且直线a不在α内,也不在β内
D.一个平面α内两条不平行的直线都平行于另一个平面β
3.在正方体ABCD-A1B1C1D1中,M是棱CD上的动点,则直线MC1与平面AA1B1B的位置关系是( )
A.相交 B.平行
C.异面 D.相交或平行
4.已知正三棱柱ABC-A1B1C1的侧棱长为4,底面边长为2.若点M是线段A1C1的中点,则直线BM与底面ABC所成角的正切值为( )
A. B. C. D.
5.已知E,F,G,H分别为四面体ABCD的棱AB,BC,DA,CD上的点,且AE=EB,BF=FC,CH=2HD,AG=2GD,则下列说法错误的是( )
A.AC∥平面EFH
B.EF∥GH
C.直线EG,FH,BD相交于同一点
D.BD∥平面EFG
6.如图,在边长为1的正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在的直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
A.无论翻折到什么位置,A、C两点都不可能重合
B.存在某个位置,使得直线AF与直线CE所成的角为60°
C.存在某个位置,使得直线AF与直线CE所成的角为90°
D.存在某个位置,使得直线AB与直线CD所成的角为90°
7.如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出五个结论:①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;④OM∥平面PBA;⑤OM∥平面PBC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
8.已知三条不重合的直线m、n、l与两个不重合的平面α、 β,有下列命题:
①若m∥n,n α,则m∥α;
②若l⊥α,m⊥β,l∥m,则α∥β;
③若m α,n α,m∥β,n∥β,则α∥β;
④若α⊥β,α∩β=m,n β,n⊥m,则n⊥α.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
9.已知正方体ABCD-A1B1C1D1的棱长为1,E是棱D1C1的中点,点F在正方体内部或正方体的表面上,且EF∥平面A1BC1,则动点F的轨迹所形成的区域面积是( )
A. B. C. D.
10.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为( )
A.90° B.60° C.45° D.30°
11.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为45°和30°.过A,B分别作两平面交线的垂线,垂足分别为A',B',则AB∶A'B'等于( )
A.2∶1 B.3∶1
C.3∶2 D.4∶3
12.如图,正三棱柱ABC-A1B1C1各条棱的长度均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中不正确的是( )
A.在△DMN内总存在与平面ABC平行的线段
B.平面DMN⊥平面BCC1B1
C.三棱锥A1-DMN的体积为定值
D.△DMN可能为直角三角形
二、填空题(本题共4小题,每小题5分,共20分)
13.已知正四棱锥的侧棱长为2,侧棱与底面所成的角为60°,则该四棱锥的高为 .
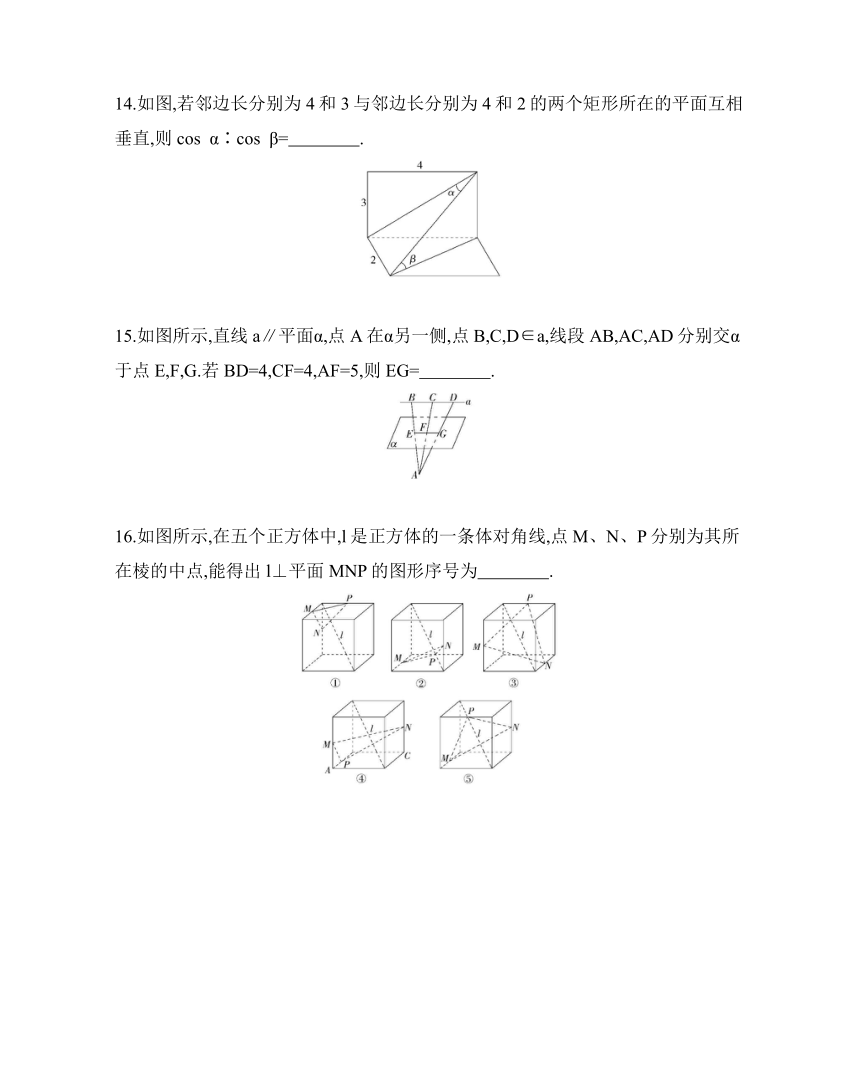
14.如图,若邻边长分别为4和3与邻边长分别为4和2的两个矩形所在的平面互相垂直,则cos α∶cos β= .
15.如图所示,直线a∥平面α,点A在α另一侧,点B,C,D∈a,线段AB,AC,AD分别交α于点E,F,G.若BD=4,CF=4,AF=5,则EG= .
16.如图所示,在五个正方体中,l是正方体的一条体对角线,点M、N、P分别为其所在棱的中点,能得出l⊥平面MNP的图形序号为 .
三、解答题(本题共6小题,共70分)
17.(10分)如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC.
(1)求证:AM⊥平面EBC;
(2)求直线EC与平面ABE所成角的正切值.
18.(12分)如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,AA1=A1C=AC,AB=BC=1,AB⊥BC,E,F分别为AC,B1C1的中点.
(1)求证:直线EF∥平面ABB1A1;
(2)求三棱锥F-ABA1的体积.
19.(12分)在四棱锥P-ABCD中,PD⊥平面ABCD,且底面ABCD是边长为2的菱形,∠BAD=60°,PD=2.
(1)证明:面PAC⊥面PDB;
(2)在图中作出点D在平面PBC内的正投影M(说明作法及其理由),并求四面体PBDM的体积.
20.(12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2,求三棱锥C-A1DE的体积.
21.(12分)如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,D是BC的中点,侧面BB1C1C⊥底面ABC.
(1)求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱AA1于点M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)若截面MBC1⊥侧面BB1C1C,则AM=MA1成立吗 请说明理由.
22.(12分)四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,△PAD是等边三角形,F为AD的中点,PD⊥BF.
(1)求证:AD⊥PB;
(2)若E在线段BC上,且EC=BC,能否在棱PC上找到一点G,使平面DEG⊥平面ABCD 若存在,求四面体DCEG的体积.
答案全解全析
一、选择题
1.D 对于①,过平面外一点可作无数个平面与已知平面垂直,故①错误;
对于②,如果一条直线和两个垂直平面中的一个垂直,那么它和另一个平面平行或在平面内,故②错误;
对于③,过不在平面内的一条直线可以作一个平面与已知平面垂直,故③错误;
对于④,如果两个平面互相垂直,那么经过一个平面内一点与另一平面垂直的直线在第一个平面内,故④正确.故选D.
2.D 对于A,α内有无数多条直线都与β平行,则α、β可能相交,A错;
对于B,直线a α,b β,且a∥β,b∥α,则α、β可能相交,B错;
对于C,直线a∥α,a∥β,且直线a不在α内,也不在β内,则α、β可能相交,C错;
对于D,一个平面内两条不平行的直线必相交,根据平面与平面平行的判定定理可知D正确.
故选D.
3.B ∵MC1 平面DD1C1C,平面AA1B1B∥平面DD1C1C,
∴MC1∥平面AA1B1B.故选B.
4.B 过点M作MN⊥AC于点N,连接BN,则∠MBN为直线BM与底面ABC所成的角.由已知可得MN=4,BN=3,所以tan∠MBN=,故选B.
5.D ∵AE=EB,BF=FC,
∴EF是△ABC的中位线,
∴EF∥AC,且EF=AC,
∵EF 平面EFH,AC 平面EFH,
∴AC∥平面EFH,故A中说法正确;
∵CH=2HD,AG=2GD,
∴GH∥AC,且GH=AC,
则EF∥GH,故B中说法正确;
∵四边形EFHG是梯形,则直线FH,EG相交,设交点为M,
则M∈EG,M∈平面ABD,M∈FH,M∈平面BCD,
则M是平面ABD和平面BCD的公共点,
则M∈BD,即直线EG,FH,BD相交于同一点,故C中说法正确,
因为AE=EB,AG=2GD,所以直线BD与EG必相交,所以D中说法错误.
故选D.
6.D 在A中,点A与点C一定不重合,故A中说法正确;
在B中,存在某个位置,使得直线AF与直线CE所成的角为60°,故B中说法正确;
在C中,当平面ABF⊥平面BEDF,平面DCE⊥平面BEDF时,直线AF与直线CE垂直,故C中说法正确;
在D中,直线AB与直线CD不可能垂直,故D错误.故选D.
7.C 因为矩形ABCD的对角线AC与BD交于O点,所以O为BD的中点.在△PBD中,M是PB的中点,所以OM是中位线,故OM∥PD,所以OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA、平面PBC相交.故正确的结论共有3个.
8.B 对于①,若m∥n,n α,则m∥α或m α,故①不正确;
对于②,若l⊥α,m⊥β,l∥m,则α∥β,显然成立;
对于③,若m α,n α,m∥β,n∥β,
当m∥n时,α与β可能相交,故③不正确;
对于④,若α⊥β,α∩β=m,n β,n⊥m,则n⊥α,由面面垂直的性质定理知它是正确的.
综上所述,正确命题的个数为2.故选B.
9.C 如图,分别取棱CC1、BC、AB、AA1、A1D1的中点M、N、G、Q、P,
则PE∥A1C1∥GN,EM∥A1B∥GQ,PQ∥BC1∥MN,
∴平面EMNGQP∥平面A1BC1,
∵点F在正方体内部或正方体的表面上,EF∥平面A1BC1,
∴动点F的轨迹所形成的区域是平面EMNGQP,
∵正方体ABCD-A1B1C1D1的棱长为1,
∴PE=EM=MN=NG=GQ=PQ=,PN=,
∴E到PN的距离d==,
∴动点F的轨迹所形成的区域面积为
S=2S梯形PNME=2××=.故选C.
10.C 当三棱锥D-ABC体积最大时,平面DAC⊥平面ABC,取AC的中点O,连接BO,DO,则△DBO是等腰直角三角形,即∠DBO=45°.
11.A 如图,连接AB',BA',则∠ABA'=30°,∠BAB'=45°.在Rt△ABB'中,=,所以AB'=AB.在Rt△AA'B中,=,所以AA'=AB.
∴在Rt△AA'B'中,A'B'=AB.故选A.
12.D A项,用平行于平面ABC的平面截平面MND,则交线平行于平面ABC,故结论正确;
B项,如图:
当M、N分别在BB1、CC1上运动时,若满足BM=C1N,则线段MN必过正方形BCC1B1的中心O,连接DO,由DO垂直于平面BCC1B1可得平面DMN⊥平面BCC1B1,故结论正确;
C项,当M、N分别在BB1、CC1上运动时,△A1DM的面积不变,N到平面A1DM的距离不变,所以棱锥N-A1DM的体积不变,即三棱锥A1-DMN的体积为定值,故结论正确;
D项,若△DMN为直角三角形,则必是以∠MDN为直角的直角三角形,但MN的最大值为BC1,而此时DM,DN的长大于BB1,所以△DMN不可能为直角三角形,故结论错误.
故选D.
二、填空题
13.答案 3
解析 如图,过点S作SO⊥平面ABCD,连接OC,则∠SCO=60°,
∴SO=sin 60°·SC=×2=3.
14.答案 ∶2
解析 由题意,两个矩形的对角线长分别为5,2,所以cos α==,
cos β=,所以cos α∶cos β=∶2.
15.答案
解析 因为A a,所以点A与直线a确定一个平面,即平面ABD.因为a∥α,且α∩平面ABD=EG,所以a∥EG,即BD∥EG,所以=.又=,所以=.于是EG===.
16.答案 ①④⑤
解析 对于①,如图所示,正方体ABCD-A'B'C'D'.
∵M、P分别为其所在棱的中点,
∴MP∥AC,
∵四边形ABCD为正方形,∴AC⊥BD,
∵BB'⊥平面ABCD,AC 平面ABCD,
∴BB'⊥AC,
∵AC⊥BD,BD∩BB'=B,
∴AC⊥平面DBB',∵DB' 平面DBB',
∴AC⊥DB'.
∵MP∥AC,∴DB'⊥MP,同理可证DB'⊥MN,DB'⊥NP,
∵MP∩NP=P,MP 平面MNP,NP 平面MNP,
∴DB'⊥平面MNP,即l垂直于平面MNP,故①正确.
对于④,易知l⊥MP,连接AC,
∵MN∥AC,AC⊥l,∴l⊥MN,
∴l⊥平面MNP,故④正确.
同理可证⑤中l⊥平面MNP.
三、解答题
17.解析 (1)证明:∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,BC⊥AC,
∴BC⊥平面ACDE.
又AM 平面ACDE,∴BC⊥AM.
∵四边形ACDE是正方形,∴AM⊥CE.
又BC∩CE=C,∴AM⊥平面EBC.
(2)如图,取AB的中点F,连接CF,EF.
∵EA⊥AC,平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,
∴EA⊥平面ABC,
∴EA⊥CF.
又AC=BC,∴CF⊥AB.
∵EA∩AB=A,
∴CF⊥平面AEB,
∴CF⊥EF,
∴∠CEF即为直线EC与平面ABE所成的角.
∵正方形ACDE的边长为2,
∴在Rt△CFE中,CF=,FE=,
∴tan∠CEF==.
18.解析 (1)证明:取A1C1的中点G,连接EG,FG,由于E,F分别为AC,B1C1的中点,所以FG∥A1B1,又A1B1 平面ABB1A1,FG 平面ABB1A1,所以FG∥平面ABB1A1.又AE∥A1G且AE=A1G,
所以四边形AEGA1是平行四边形.
所以EG∥AA1又AA1 平面ABB1A1,EG 平面ABB1A1,
所以EG∥平面ABB1A1.
所以平面EFG∥平面ABB1A1.
又EF 平面EFG,
所以直线EF∥平面ABB1A1.
(2)因为AB=BC=1,AB⊥BC,
所以AA1=A1C=AC=,
连接A1E,由于E为AC的中点,所以A1E⊥AC,又侧面AA1C1C⊥底面ABC,
交线为AC,A1E 平面AA1C1C,
则A1E⊥平面ABC,连接EB,可知EB,EA,EA1两两垂直.
由(1)知直线EF∥平面ABA1,=== ×EB·EA·EA1=.
19.解析 (1)证明:因为PD⊥平面ABCD,AC 面ABCD,所以PD⊥AC.
在菱形ABCD中,AC⊥BD,且PD∩BD=D,
所以AC⊥面PBD,
又因为AC 面PAC,
所以面PAC⊥面PDB .
(2)取BC的中点E,连接DE,PE,易得△BDC是等边三角形,
所以BC⊥DE,
又因为PD⊥面ABCD,
所以PD⊥BC,
又PD∩DE=D,
所以BC⊥面PDE,
在面PDE中,过D作DM⊥PE于M,则DM⊥BC,
又BC∩PE=E,
所以DM⊥面PBC,
即M是点D在平面PBC内的正投影,
经计算得DE=,在Rt△PDE中,PD=2,PE==,
DM==,PM==,所以VD-PBM=×S△PBM×DM=×××1×=.
20.解析 (1)证明:如图,连接AC1交A1C于点F,连接DF,
则F为AC1的中点.
因为D是AB的中点,所以BC1∥DF.
因为DF 平面A1CD,BC1 平面A1CD,
所以BC1∥平面A1CD.
(2)因为三棱柱ABC-A1B1C1是直三棱柱,
所以AA1⊥CD.由已知AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2得,
∠ACB=90°,CD=,A1D=,DE=,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以=××××=1.
21.解析 (1)证明:∵AB=AC,D是BC的中点,∴AD⊥BC.
∵底面ABC⊥侧面BB1C1C,底面ABC∩侧面BB1C1C=BC,
∴AD⊥侧面BB1C1C.
又CC1 侧面BB1C1C,∴AD⊥CC1.
(2)证明:如图,延长B1A1与BM的延长线交于点N,连接C1N.
∵AM=MA1,∴NA1=A1B1.∵A1B1=A1C1,
∴A1C1=A1N=A1B1,
∴C1N⊥B1C1,∴C1N⊥侧面BB1C1C.
∵C1N 平面MBC1,
∴截面MBC1⊥侧面BB1C1C.
(3)成立.过M作ME⊥BC1于点E,连接DE.
∵截面MBC1⊥侧面BB1C1C,
∴ME⊥侧面BB1C1C.
又AD⊥侧面BB1C1C,∴ME∥AD,
∴M,E,D,A四点共面.
∵MA∥侧面BB1C1C,∴AM∥DE.
∴四边形AMED是平行四边形,
又AM∥CC1,∴DE∥CC1.
∵D是BC的中点,∴DE=CC1,
∴AM=CC1=AA1.∴AM=MA1.
22.解析 (1)证明:连接PF,BD,
∵△PAD是等边三角形,F为AD的中点,
∴PF⊥AD,
∵底面ABCD是菱形,∠BAD=60°,
∴△ABD是等边三角形,
∵F为AD的中点,
∴BF⊥AD,
又PF,BF 平面PBF,PF∩BF=F,
∴AD⊥平面PBF,∵PB 平面PBF,
∴AD⊥PB.
(2)由(1)得BF⊥AD,又∵PD⊥BF,AD,PD 平面PAD,
∴BF⊥平面PAD,又BF 平面ABCD,
∴平面PAD⊥平面ABCD,
由(1)得PF⊥AD,平面PAD∩平面ABCD=AD,
∴PF⊥平面ABCD,
连接FC交DE于H,则△HEC与△HDF相似,又EC=BC=FD,∴CH=CF,
∴在△PFC中,过H作GH∥PF交PC于G,则GH⊥平面ABCD,又GH 平面GED,则平面GED⊥平面ABCD,此时CG=CP,
∴四面体DCEG的体积VD-CEG=VG-CED=S△CED·GH=××2×2××PF=.
所以存在G满足CG=CP, 使平面DEG⊥平面ABCD,且VD-CEG=.
一、选择题(本题共12小题,每小题5分,共60分)
1.下列命题正确的是( )
①过平面外一点有且仅有一个平面与已知平面垂直;
②如果一条直线和两个垂直平面中的一个垂直,那么它必和另一个平面平行;
③过不在平面内的一条直线可作无数个平面与已知平面垂直;
④如果两个平面互相垂直,那么经过一个平面内一点与另一平面垂直的直线在第一个平面内.
A.①③ B.②③
C.②③④ D.④
2.平面α与平面β平行的条件可以是( )
A.α内有无数多条直线都与β平行
B.直线a α,b β,且a∥β,b∥α
C.直线a∥α,a∥β,且直线a不在α内,也不在β内
D.一个平面α内两条不平行的直线都平行于另一个平面β
3.在正方体ABCD-A1B1C1D1中,M是棱CD上的动点,则直线MC1与平面AA1B1B的位置关系是( )
A.相交 B.平行
C.异面 D.相交或平行
4.已知正三棱柱ABC-A1B1C1的侧棱长为4,底面边长为2.若点M是线段A1C1的中点,则直线BM与底面ABC所成角的正切值为( )
A. B. C. D.
5.已知E,F,G,H分别为四面体ABCD的棱AB,BC,DA,CD上的点,且AE=EB,BF=FC,CH=2HD,AG=2GD,则下列说法错误的是( )
A.AC∥平面EFH
B.EF∥GH
C.直线EG,FH,BD相交于同一点
D.BD∥平面EFG
6.如图,在边长为1的正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在的直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
A.无论翻折到什么位置,A、C两点都不可能重合
B.存在某个位置,使得直线AF与直线CE所成的角为60°
C.存在某个位置,使得直线AF与直线CE所成的角为90°
D.存在某个位置,使得直线AB与直线CD所成的角为90°
7.如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出五个结论:①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;④OM∥平面PBA;⑤OM∥平面PBC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
8.已知三条不重合的直线m、n、l与两个不重合的平面α、 β,有下列命题:
①若m∥n,n α,则m∥α;
②若l⊥α,m⊥β,l∥m,则α∥β;
③若m α,n α,m∥β,n∥β,则α∥β;
④若α⊥β,α∩β=m,n β,n⊥m,则n⊥α.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
9.已知正方体ABCD-A1B1C1D1的棱长为1,E是棱D1C1的中点,点F在正方体内部或正方体的表面上,且EF∥平面A1BC1,则动点F的轨迹所形成的区域面积是( )
A. B. C. D.
10.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为( )
A.90° B.60° C.45° D.30°
11.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为45°和30°.过A,B分别作两平面交线的垂线,垂足分别为A',B',则AB∶A'B'等于( )
A.2∶1 B.3∶1
C.3∶2 D.4∶3
12.如图,正三棱柱ABC-A1B1C1各条棱的长度均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中不正确的是( )
A.在△DMN内总存在与平面ABC平行的线段
B.平面DMN⊥平面BCC1B1
C.三棱锥A1-DMN的体积为定值
D.△DMN可能为直角三角形
二、填空题(本题共4小题,每小题5分,共20分)
13.已知正四棱锥的侧棱长为2,侧棱与底面所成的角为60°,则该四棱锥的高为 .
14.如图,若邻边长分别为4和3与邻边长分别为4和2的两个矩形所在的平面互相垂直,则cos α∶cos β= .
15.如图所示,直线a∥平面α,点A在α另一侧,点B,C,D∈a,线段AB,AC,AD分别交α于点E,F,G.若BD=4,CF=4,AF=5,则EG= .
16.如图所示,在五个正方体中,l是正方体的一条体对角线,点M、N、P分别为其所在棱的中点,能得出l⊥平面MNP的图形序号为 .
三、解答题(本题共6小题,共70分)
17.(10分)如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC.
(1)求证:AM⊥平面EBC;
(2)求直线EC与平面ABE所成角的正切值.
18.(12分)如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,AA1=A1C=AC,AB=BC=1,AB⊥BC,E,F分别为AC,B1C1的中点.
(1)求证:直线EF∥平面ABB1A1;
(2)求三棱锥F-ABA1的体积.
19.(12分)在四棱锥P-ABCD中,PD⊥平面ABCD,且底面ABCD是边长为2的菱形,∠BAD=60°,PD=2.
(1)证明:面PAC⊥面PDB;
(2)在图中作出点D在平面PBC内的正投影M(说明作法及其理由),并求四面体PBDM的体积.
20.(12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2,求三棱锥C-A1DE的体积.
21.(12分)如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,D是BC的中点,侧面BB1C1C⊥底面ABC.
(1)求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱AA1于点M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)若截面MBC1⊥侧面BB1C1C,则AM=MA1成立吗 请说明理由.
22.(12分)四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,△PAD是等边三角形,F为AD的中点,PD⊥BF.
(1)求证:AD⊥PB;
(2)若E在线段BC上,且EC=BC,能否在棱PC上找到一点G,使平面DEG⊥平面ABCD 若存在,求四面体DCEG的体积.
答案全解全析
一、选择题
1.D 对于①,过平面外一点可作无数个平面与已知平面垂直,故①错误;
对于②,如果一条直线和两个垂直平面中的一个垂直,那么它和另一个平面平行或在平面内,故②错误;
对于③,过不在平面内的一条直线可以作一个平面与已知平面垂直,故③错误;
对于④,如果两个平面互相垂直,那么经过一个平面内一点与另一平面垂直的直线在第一个平面内,故④正确.故选D.
2.D 对于A,α内有无数多条直线都与β平行,则α、β可能相交,A错;
对于B,直线a α,b β,且a∥β,b∥α,则α、β可能相交,B错;
对于C,直线a∥α,a∥β,且直线a不在α内,也不在β内,则α、β可能相交,C错;
对于D,一个平面内两条不平行的直线必相交,根据平面与平面平行的判定定理可知D正确.
故选D.
3.B ∵MC1 平面DD1C1C,平面AA1B1B∥平面DD1C1C,
∴MC1∥平面AA1B1B.故选B.
4.B 过点M作MN⊥AC于点N,连接BN,则∠MBN为直线BM与底面ABC所成的角.由已知可得MN=4,BN=3,所以tan∠MBN=,故选B.
5.D ∵AE=EB,BF=FC,
∴EF是△ABC的中位线,
∴EF∥AC,且EF=AC,
∵EF 平面EFH,AC 平面EFH,
∴AC∥平面EFH,故A中说法正确;
∵CH=2HD,AG=2GD,
∴GH∥AC,且GH=AC,
则EF∥GH,故B中说法正确;
∵四边形EFHG是梯形,则直线FH,EG相交,设交点为M,
则M∈EG,M∈平面ABD,M∈FH,M∈平面BCD,
则M是平面ABD和平面BCD的公共点,
则M∈BD,即直线EG,FH,BD相交于同一点,故C中说法正确,
因为AE=EB,AG=2GD,所以直线BD与EG必相交,所以D中说法错误.
故选D.
6.D 在A中,点A与点C一定不重合,故A中说法正确;
在B中,存在某个位置,使得直线AF与直线CE所成的角为60°,故B中说法正确;
在C中,当平面ABF⊥平面BEDF,平面DCE⊥平面BEDF时,直线AF与直线CE垂直,故C中说法正确;
在D中,直线AB与直线CD不可能垂直,故D错误.故选D.
7.C 因为矩形ABCD的对角线AC与BD交于O点,所以O为BD的中点.在△PBD中,M是PB的中点,所以OM是中位线,故OM∥PD,所以OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA、平面PBC相交.故正确的结论共有3个.
8.B 对于①,若m∥n,n α,则m∥α或m α,故①不正确;
对于②,若l⊥α,m⊥β,l∥m,则α∥β,显然成立;
对于③,若m α,n α,m∥β,n∥β,
当m∥n时,α与β可能相交,故③不正确;
对于④,若α⊥β,α∩β=m,n β,n⊥m,则n⊥α,由面面垂直的性质定理知它是正确的.
综上所述,正确命题的个数为2.故选B.
9.C 如图,分别取棱CC1、BC、AB、AA1、A1D1的中点M、N、G、Q、P,
则PE∥A1C1∥GN,EM∥A1B∥GQ,PQ∥BC1∥MN,
∴平面EMNGQP∥平面A1BC1,
∵点F在正方体内部或正方体的表面上,EF∥平面A1BC1,
∴动点F的轨迹所形成的区域是平面EMNGQP,
∵正方体ABCD-A1B1C1D1的棱长为1,
∴PE=EM=MN=NG=GQ=PQ=,PN=,
∴E到PN的距离d==,
∴动点F的轨迹所形成的区域面积为
S=2S梯形PNME=2××=.故选C.
10.C 当三棱锥D-ABC体积最大时,平面DAC⊥平面ABC,取AC的中点O,连接BO,DO,则△DBO是等腰直角三角形,即∠DBO=45°.
11.A 如图,连接AB',BA',则∠ABA'=30°,∠BAB'=45°.在Rt△ABB'中,=,所以AB'=AB.在Rt△AA'B中,=,所以AA'=AB.
∴在Rt△AA'B'中,A'B'=AB.故选A.
12.D A项,用平行于平面ABC的平面截平面MND,则交线平行于平面ABC,故结论正确;
B项,如图:
当M、N分别在BB1、CC1上运动时,若满足BM=C1N,则线段MN必过正方形BCC1B1的中心O,连接DO,由DO垂直于平面BCC1B1可得平面DMN⊥平面BCC1B1,故结论正确;
C项,当M、N分别在BB1、CC1上运动时,△A1DM的面积不变,N到平面A1DM的距离不变,所以棱锥N-A1DM的体积不变,即三棱锥A1-DMN的体积为定值,故结论正确;
D项,若△DMN为直角三角形,则必是以∠MDN为直角的直角三角形,但MN的最大值为BC1,而此时DM,DN的长大于BB1,所以△DMN不可能为直角三角形,故结论错误.
故选D.
二、填空题
13.答案 3
解析 如图,过点S作SO⊥平面ABCD,连接OC,则∠SCO=60°,
∴SO=sin 60°·SC=×2=3.
14.答案 ∶2
解析 由题意,两个矩形的对角线长分别为5,2,所以cos α==,
cos β=,所以cos α∶cos β=∶2.
15.答案
解析 因为A a,所以点A与直线a确定一个平面,即平面ABD.因为a∥α,且α∩平面ABD=EG,所以a∥EG,即BD∥EG,所以=.又=,所以=.于是EG===.
16.答案 ①④⑤
解析 对于①,如图所示,正方体ABCD-A'B'C'D'.
∵M、P分别为其所在棱的中点,
∴MP∥AC,
∵四边形ABCD为正方形,∴AC⊥BD,
∵BB'⊥平面ABCD,AC 平面ABCD,
∴BB'⊥AC,
∵AC⊥BD,BD∩BB'=B,
∴AC⊥平面DBB',∵DB' 平面DBB',
∴AC⊥DB'.
∵MP∥AC,∴DB'⊥MP,同理可证DB'⊥MN,DB'⊥NP,
∵MP∩NP=P,MP 平面MNP,NP 平面MNP,
∴DB'⊥平面MNP,即l垂直于平面MNP,故①正确.
对于④,易知l⊥MP,连接AC,
∵MN∥AC,AC⊥l,∴l⊥MN,
∴l⊥平面MNP,故④正确.
同理可证⑤中l⊥平面MNP.
三、解答题
17.解析 (1)证明:∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,BC⊥AC,
∴BC⊥平面ACDE.
又AM 平面ACDE,∴BC⊥AM.
∵四边形ACDE是正方形,∴AM⊥CE.
又BC∩CE=C,∴AM⊥平面EBC.
(2)如图,取AB的中点F,连接CF,EF.
∵EA⊥AC,平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,
∴EA⊥平面ABC,
∴EA⊥CF.
又AC=BC,∴CF⊥AB.
∵EA∩AB=A,
∴CF⊥平面AEB,
∴CF⊥EF,
∴∠CEF即为直线EC与平面ABE所成的角.
∵正方形ACDE的边长为2,
∴在Rt△CFE中,CF=,FE=,
∴tan∠CEF==.
18.解析 (1)证明:取A1C1的中点G,连接EG,FG,由于E,F分别为AC,B1C1的中点,所以FG∥A1B1,又A1B1 平面ABB1A1,FG 平面ABB1A1,所以FG∥平面ABB1A1.又AE∥A1G且AE=A1G,
所以四边形AEGA1是平行四边形.
所以EG∥AA1又AA1 平面ABB1A1,EG 平面ABB1A1,
所以EG∥平面ABB1A1.
所以平面EFG∥平面ABB1A1.
又EF 平面EFG,
所以直线EF∥平面ABB1A1.
(2)因为AB=BC=1,AB⊥BC,
所以AA1=A1C=AC=,
连接A1E,由于E为AC的中点,所以A1E⊥AC,又侧面AA1C1C⊥底面ABC,
交线为AC,A1E 平面AA1C1C,
则A1E⊥平面ABC,连接EB,可知EB,EA,EA1两两垂直.
由(1)知直线EF∥平面ABA1,=== ×EB·EA·EA1=.
19.解析 (1)证明:因为PD⊥平面ABCD,AC 面ABCD,所以PD⊥AC.
在菱形ABCD中,AC⊥BD,且PD∩BD=D,
所以AC⊥面PBD,
又因为AC 面PAC,
所以面PAC⊥面PDB .
(2)取BC的中点E,连接DE,PE,易得△BDC是等边三角形,
所以BC⊥DE,
又因为PD⊥面ABCD,
所以PD⊥BC,
又PD∩DE=D,
所以BC⊥面PDE,
在面PDE中,过D作DM⊥PE于M,则DM⊥BC,
又BC∩PE=E,
所以DM⊥面PBC,
即M是点D在平面PBC内的正投影,
经计算得DE=,在Rt△PDE中,PD=2,PE==,
DM==,PM==,所以VD-PBM=×S△PBM×DM=×××1×=.
20.解析 (1)证明:如图,连接AC1交A1C于点F,连接DF,
则F为AC1的中点.
因为D是AB的中点,所以BC1∥DF.
因为DF 平面A1CD,BC1 平面A1CD,
所以BC1∥平面A1CD.
(2)因为三棱柱ABC-A1B1C1是直三棱柱,
所以AA1⊥CD.由已知AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2得,
∠ACB=90°,CD=,A1D=,DE=,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以=××××=1.
21.解析 (1)证明:∵AB=AC,D是BC的中点,∴AD⊥BC.
∵底面ABC⊥侧面BB1C1C,底面ABC∩侧面BB1C1C=BC,
∴AD⊥侧面BB1C1C.
又CC1 侧面BB1C1C,∴AD⊥CC1.
(2)证明:如图,延长B1A1与BM的延长线交于点N,连接C1N.
∵AM=MA1,∴NA1=A1B1.∵A1B1=A1C1,
∴A1C1=A1N=A1B1,
∴C1N⊥B1C1,∴C1N⊥侧面BB1C1C.
∵C1N 平面MBC1,
∴截面MBC1⊥侧面BB1C1C.
(3)成立.过M作ME⊥BC1于点E,连接DE.
∵截面MBC1⊥侧面BB1C1C,
∴ME⊥侧面BB1C1C.
又AD⊥侧面BB1C1C,∴ME∥AD,
∴M,E,D,A四点共面.
∵MA∥侧面BB1C1C,∴AM∥DE.
∴四边形AMED是平行四边形,
又AM∥CC1,∴DE∥CC1.
∵D是BC的中点,∴DE=CC1,
∴AM=CC1=AA1.∴AM=MA1.
22.解析 (1)证明:连接PF,BD,
∵△PAD是等边三角形,F为AD的中点,
∴PF⊥AD,
∵底面ABCD是菱形,∠BAD=60°,
∴△ABD是等边三角形,
∵F为AD的中点,
∴BF⊥AD,
又PF,BF 平面PBF,PF∩BF=F,
∴AD⊥平面PBF,∵PB 平面PBF,
∴AD⊥PB.
(2)由(1)得BF⊥AD,又∵PD⊥BF,AD,PD 平面PAD,
∴BF⊥平面PAD,又BF 平面ABCD,
∴平面PAD⊥平面ABCD,
由(1)得PF⊥AD,平面PAD∩平面ABCD=AD,
∴PF⊥平面ABCD,
连接FC交DE于H,则△HEC与△HDF相似,又EC=BC=FD,∴CH=CF,
∴在△PFC中,过H作GH∥PF交PC于G,则GH⊥平面ABCD,又GH 平面GED,则平面GED⊥平面ABCD,此时CG=CP,
∴四面体DCEG的体积VD-CEG=VG-CED=S△CED·GH=××2×2××PF=.
所以存在G满足CG=CP, 使平面DEG⊥平面ABCD,且VD-CEG=.
