冀教版九年级下册课时作业 29.3切线的性质和判定(word版含答案)
文档属性
| 名称 | 冀教版九年级下册课时作业 29.3切线的性质和判定(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 471.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 08:46:06 | ||
图片预览

文档简介
29.3切线的性质和判定
一、单选题
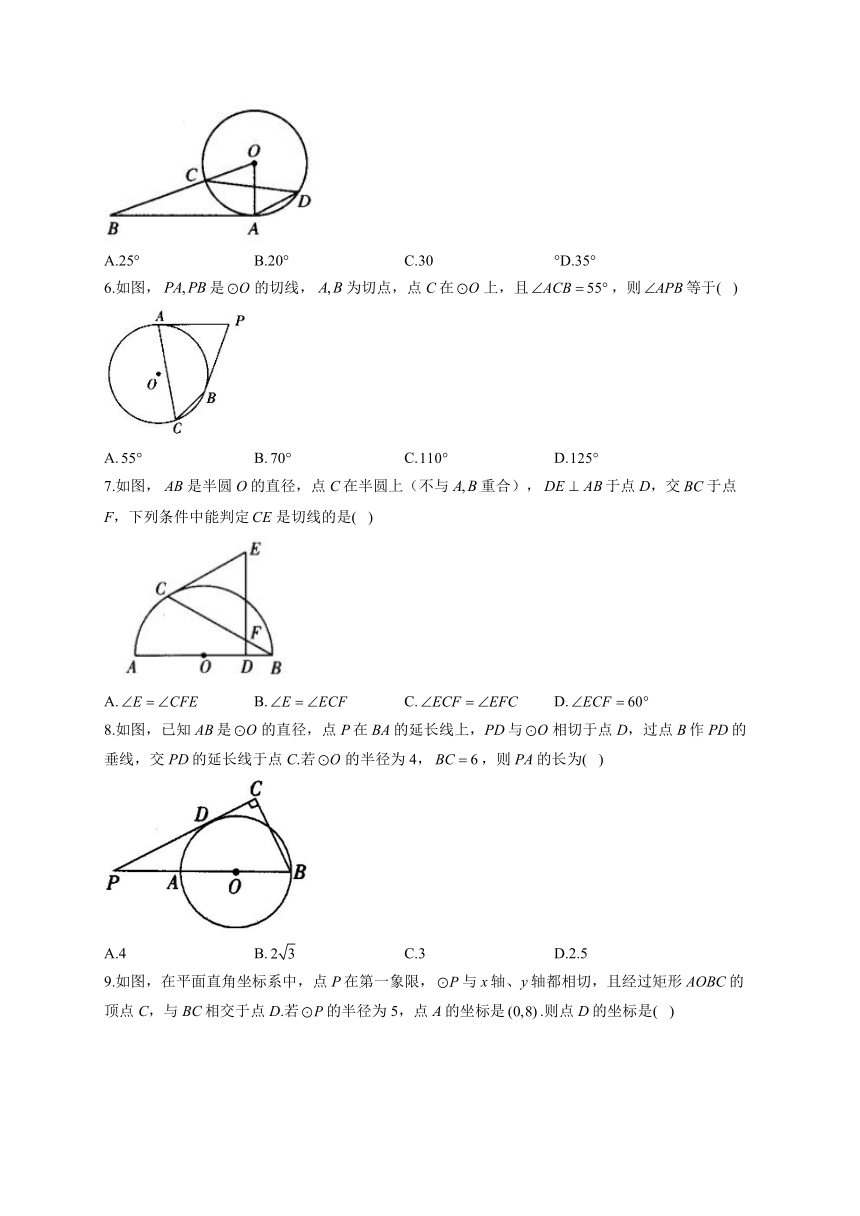
1.已知的半径为5,直线EF经过上一点P(点E,F在点P的两旁),下列条件能判定直线EF与相切的是( )
A. B. C.点O到直线EF的距离是4 D.
2.如图,AB是的直径,点P,Q在上,过点P的切线与AB的延长线交于点C,连接AQ,PQ.若,则的度数为( )
A.66° B.65° C.64° D.63°
3.如图,点P为外一点,PA为的切线,A为切点,交于点B,,,则线段BP的长为( )
A.3 B. C.6 D.9
4.下列直线一定是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆的直径端点的直线
5.如图,为的切线,点为切点,交于点,点在上,连接,若,则的度数为( )
A.25° B.20° C.30 °D.35°
6.如图,是的切线,为切点,点C在上,且,则等于( )
A. B. C. D.
7.如图,是半圆O的直径,点C在半圆上(不与重合),于点D,交于点F,下列条件中能判定是切线的是( )
A. B. C. D.
8.如图,已知AB是的直径,点P在BA的延长线上,PD与相切于点D,过点B作PD的垂线,交PD的延长线于点C.若的半径为4,,则PA的长为( )
A.4 B. C.3 D.2.5
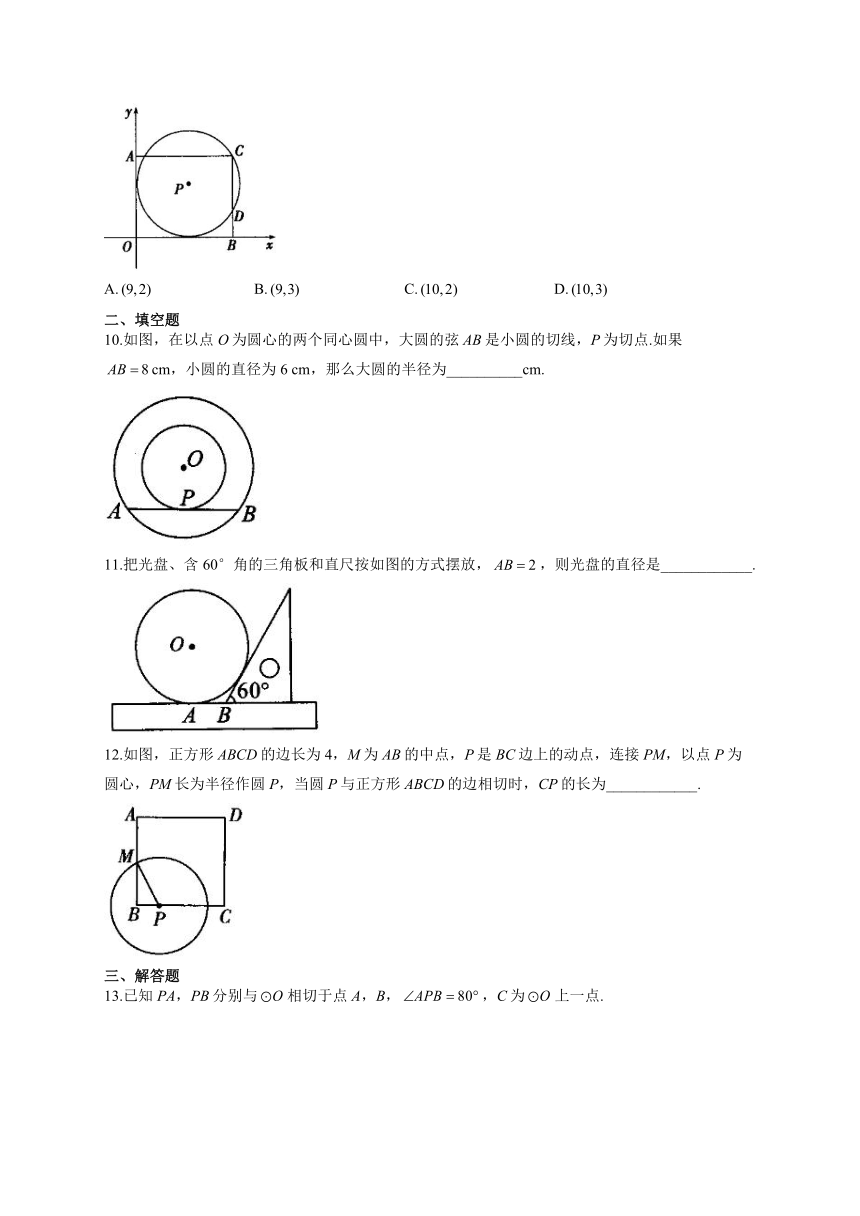
9.如图,在平面直角坐标系中,点P在第一象限,与x轴、y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D.若的半径为5,点A的坐标是.则点D的坐标是( )
A. B. C. D.
二、填空题
10.如图,在以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,P为切点.如果cm,小圆的直径为6 cm,那么大圆的半径为__________cm.
11.把光盘、含60°角的三角板和直尺按如图的方式摆放,,则光盘的直径是____________.
12.如图,正方形ABCD的边长为4,M为AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作圆P,当圆P与正方形ABCD的边相切时,CP的长为____________.
三、解答题
13.已知PA,PB分别与相切于点A,B,,C为上一点.
(1)如图(1),求的大小.
(2)如图(2),AE为的直径,AE与BC相交于点D.若,求的大小.
参考答案
1.答案:D
解析:点P在上,只需要即可.故选D.
2.答案:D
解析:如答图,连接OP.PC是的切线,.,,,.故选D.
3.答案:A
解析:连接OA.PA为的切线,.,,,则,.
4.答案:B
解析:与圆只有一个公共点的直线是圆的切线,A选项不符合题意;由到圆心的距离等于半径的直线易知该直线与此圆只有一个公共点,即该直线为此圆的切线,B选项符合题意;圆的切线垂直于圆的半径且经过半径的外端点,C选项不符合题意;过圆的直径端点且与该直径垂直的直线是圆的切线,D选项不符合题意.故选B.
5.答案:B
解析:本题考查圆的切线的性质、圆周角定理.切于点,.,故选B.
6.答案:B
解析:如图,连接.是的切线,.
又,
.
7.答案:C
解析:如图,连接.
,
,
,
,
,是的切线.故选C.
8.答案:A
解析:本题考查圆的基本性质、切线的性质、平行线的判定、相似三角形的判定和性质.连接OD,PC是的切线,,,的半径是4,,又,,解得,故选A.
9.答案:A
解析:如图,设与x轴,y轴相切的切点分别是F,E点,连接PE,PF,PC,PD,延长EP与CD交于点G,则轴,轴.,四边形PEOF是矩形.,四边形PEOF为正方形,.,,.四边形OACB为矩形,,,.,,四边形AEGC为平行四边形,四边形OEGB为平行四边形,,.,,.,,.,,,,.故选A.
10.答案:5
解析:如答图,连接OP,AO.AB是小圆的切线,.又OP经过圆心,cm,(cm).小圆的直径为6 cm, cm.在中,由勾股定理得(cm),即大圆的半径为5 cm.
11.答案:
解析:如答图,设三角板与圆的切点为C,连接OA,OB,OC.AB,BC分别与相切于点A,C,.在和中,,,,.在中,,光盘的直径为.
12.答案:2.5或
解析:如图(1),当与CD相切时,设,则.M为AB的中点,.在中,,,,.如图(2),当与AD相切时.设切点为K,连接PK,则,四边形PKDC是矩形.
.,.在中,,.综上所述,CP的长为2.5或.故答案是2.5或.
13.答案:(1)连接OA,OB.
PA,PB是的切线,
,
.
由圆周角定理得,.
(2)连接CE.
AE为的直径,.
,,
.
,,
.
一、单选题
1.已知的半径为5,直线EF经过上一点P(点E,F在点P的两旁),下列条件能判定直线EF与相切的是( )
A. B. C.点O到直线EF的距离是4 D.
2.如图,AB是的直径,点P,Q在上,过点P的切线与AB的延长线交于点C,连接AQ,PQ.若,则的度数为( )
A.66° B.65° C.64° D.63°
3.如图,点P为外一点,PA为的切线,A为切点,交于点B,,,则线段BP的长为( )
A.3 B. C.6 D.9
4.下列直线一定是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆的直径端点的直线
5.如图,为的切线,点为切点,交于点,点在上,连接,若,则的度数为( )
A.25° B.20° C.30 °D.35°
6.如图,是的切线,为切点,点C在上,且,则等于( )
A. B. C. D.
7.如图,是半圆O的直径,点C在半圆上(不与重合),于点D,交于点F,下列条件中能判定是切线的是( )
A. B. C. D.
8.如图,已知AB是的直径,点P在BA的延长线上,PD与相切于点D,过点B作PD的垂线,交PD的延长线于点C.若的半径为4,,则PA的长为( )
A.4 B. C.3 D.2.5
9.如图,在平面直角坐标系中,点P在第一象限,与x轴、y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D.若的半径为5,点A的坐标是.则点D的坐标是( )
A. B. C. D.
二、填空题
10.如图,在以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,P为切点.如果cm,小圆的直径为6 cm,那么大圆的半径为__________cm.
11.把光盘、含60°角的三角板和直尺按如图的方式摆放,,则光盘的直径是____________.
12.如图,正方形ABCD的边长为4,M为AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作圆P,当圆P与正方形ABCD的边相切时,CP的长为____________.
三、解答题
13.已知PA,PB分别与相切于点A,B,,C为上一点.
(1)如图(1),求的大小.
(2)如图(2),AE为的直径,AE与BC相交于点D.若,求的大小.
参考答案
1.答案:D
解析:点P在上,只需要即可.故选D.
2.答案:D
解析:如答图,连接OP.PC是的切线,.,,,.故选D.
3.答案:A
解析:连接OA.PA为的切线,.,,,则,.
4.答案:B
解析:与圆只有一个公共点的直线是圆的切线,A选项不符合题意;由到圆心的距离等于半径的直线易知该直线与此圆只有一个公共点,即该直线为此圆的切线,B选项符合题意;圆的切线垂直于圆的半径且经过半径的外端点,C选项不符合题意;过圆的直径端点且与该直径垂直的直线是圆的切线,D选项不符合题意.故选B.
5.答案:B
解析:本题考查圆的切线的性质、圆周角定理.切于点,.,故选B.
6.答案:B
解析:如图,连接.是的切线,.
又,
.
7.答案:C
解析:如图,连接.
,
,
,
,
,是的切线.故选C.
8.答案:A
解析:本题考查圆的基本性质、切线的性质、平行线的判定、相似三角形的判定和性质.连接OD,PC是的切线,,,的半径是4,,又,,解得,故选A.
9.答案:A
解析:如图,设与x轴,y轴相切的切点分别是F,E点,连接PE,PF,PC,PD,延长EP与CD交于点G,则轴,轴.,四边形PEOF是矩形.,四边形PEOF为正方形,.,,.四边形OACB为矩形,,,.,,四边形AEGC为平行四边形,四边形OEGB为平行四边形,,.,,.,,.,,,,.故选A.
10.答案:5
解析:如答图,连接OP,AO.AB是小圆的切线,.又OP经过圆心,cm,(cm).小圆的直径为6 cm, cm.在中,由勾股定理得(cm),即大圆的半径为5 cm.
11.答案:
解析:如答图,设三角板与圆的切点为C,连接OA,OB,OC.AB,BC分别与相切于点A,C,.在和中,,,,.在中,,光盘的直径为.
12.答案:2.5或
解析:如图(1),当与CD相切时,设,则.M为AB的中点,.在中,,,,.如图(2),当与AD相切时.设切点为K,连接PK,则,四边形PKDC是矩形.
.,.在中,,.综上所述,CP的长为2.5或.故答案是2.5或.
13.答案:(1)连接OA,OB.
PA,PB是的切线,
,
.
由圆周角定理得,.
(2)连接CE.
AE为的直径,.
,,
.
,,
.
