冀教版九年级下册课时作业 30.4二次函数的应用(word版含答案)
文档属性
| 名称 | 冀教版九年级下册课时作业 30.4二次函数的应用(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 500.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 00:00:00 | ||
图片预览

文档简介
30.4二次函数的应用
一、单选题
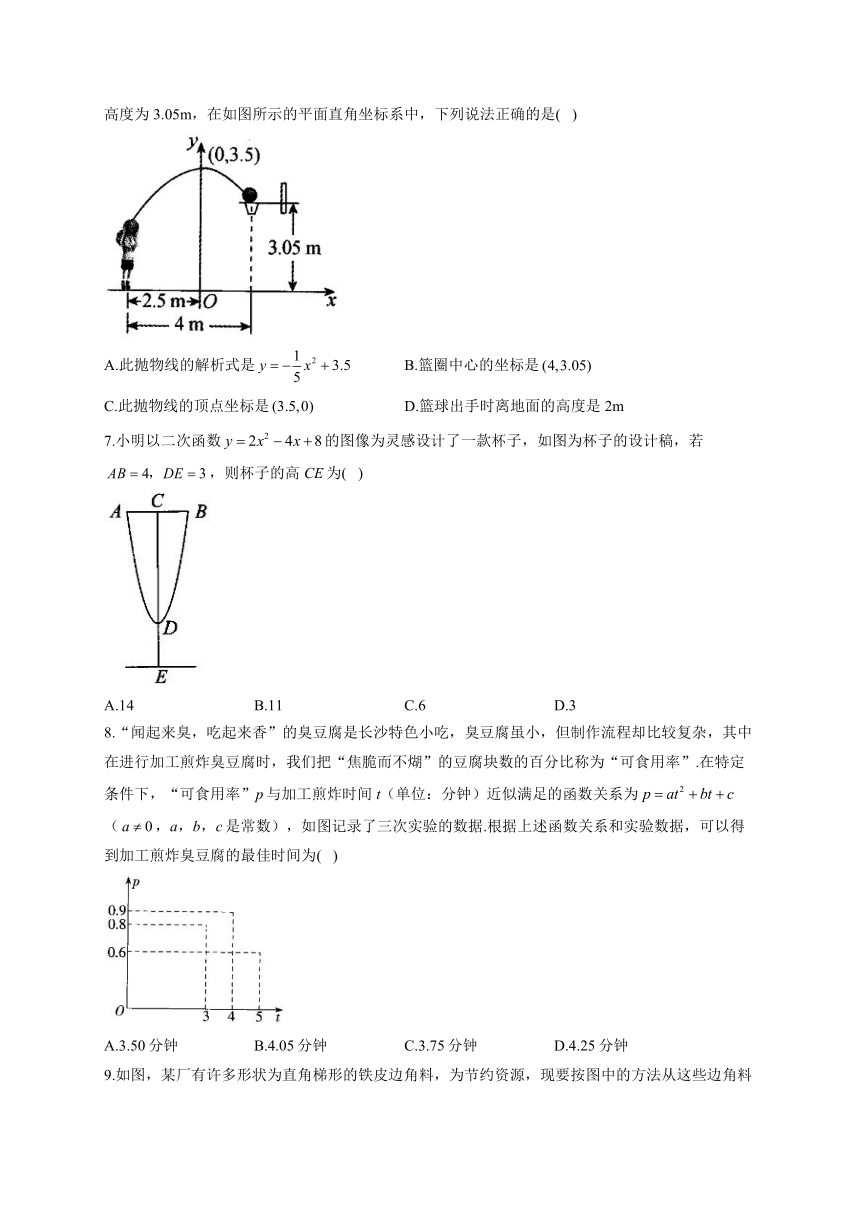
1.便民商店经营一种商品,在销售过程中发现一周所获利润y(元)与每件销售价x(元)之间满足关系式,由于某种原因,价格只能满足,那么一周可获得的最大利润是( )
A.1554元 B.1556元 C.1558元 D.1560元
2.如图,点是线段上的一动点,,分别以和为一边作正方形,用表示这两个正方形的面积之和,下列判断正确的是( )
A.当是的中点时,最小 B.当是的中点时,最大
C.当是的三等分点时,最小 D.当是的三等分点时,最大
3.如图,矩形中,,,点从出发,以每秒2个单位沿运动,同时点也从出发,以每秒1个单位沿运动,的面积为,运动的时间为秒,则关于的函数图象为( )
A. B. C. D.
4.竖直上抛物体离地面的高度与运动时间之间的关系可以近似地用公式表示,其中是物体抛出时离地面的高度,是物体抛出时的速度.某人将一个小球从距地面的高处以的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A. B. C. D.
5.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,则能获取的最大利润是( )
A.600元 B.625元 C.650元 D.675元
6.一位篮球运动员在距篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动到与球出手处水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面的高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是 B.篮圈中心的坐标是
C.此抛物线的顶点坐标是 D.篮球出手时离地面的高度是2m
7.小明以二次函数的图像为灵感设计了一款杯子,如图为杯子的设计稿,若,则杯子的高CE为( )
A.14 B.11 C.6 D.3
8.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不煳”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”p与加工煎炸时间t(单位:分钟)近似满足的函数关系为(,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
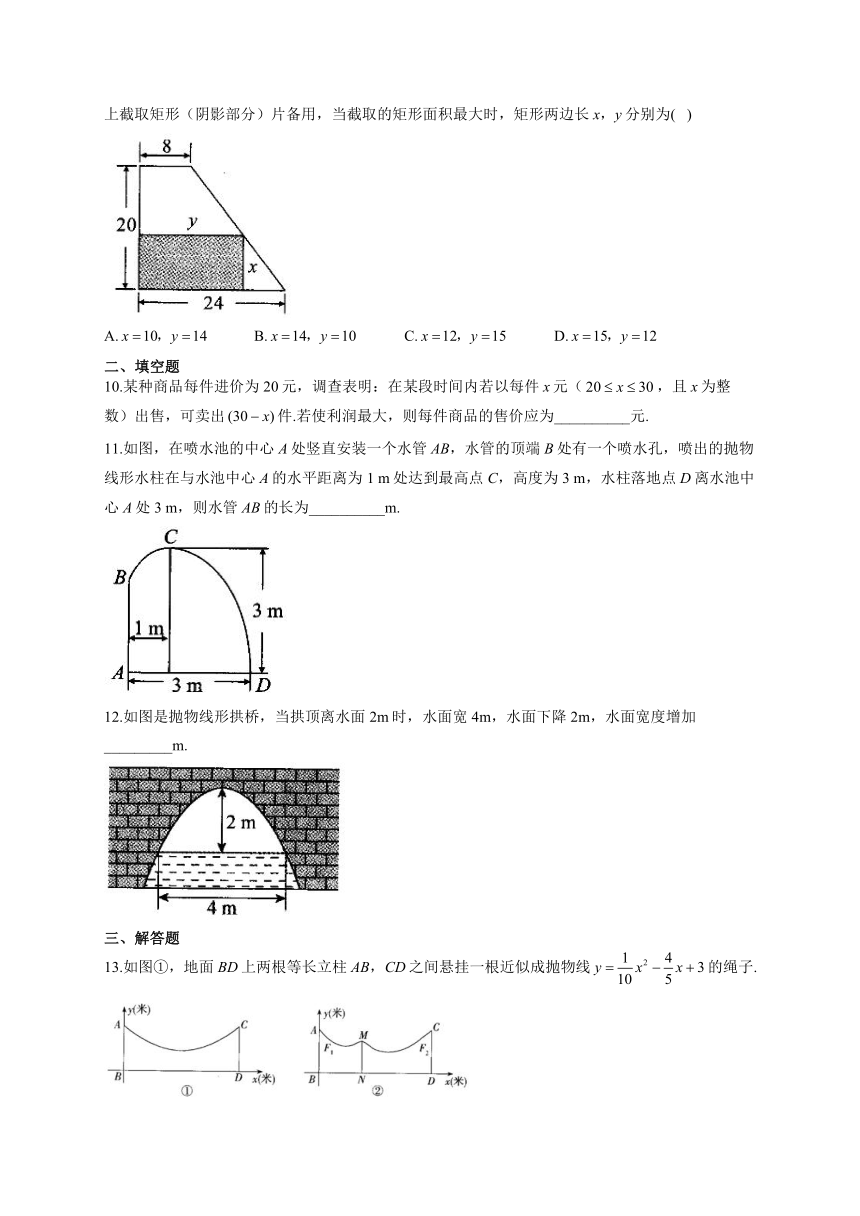
9.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中的方法从这些边角料上截取矩形(阴影部分)片备用,当截取的矩形面积最大时,矩形两边长x,y分别为( )
A. B. C. D.
二、填空题
10.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(,且x为整数)出售,可卖出件.若使利润最大,则每件商品的售价应为__________元.
11.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与水池中心A的水平距离为1 m处达到最高点C,高度为3 m,水柱落地点D离水池中心A处3 m,则水管AB的长为__________m.
12.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加_________m.
三、解答题
13.如图①,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线的绳子.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图②),使左边抛物线的最低点距MN1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线对应函数的二次项系数始终为.设MN离AB的距离为m,抛物线的顶点离地面的距离为k,当时,求m的取值范围.
参考答案
1.答案:B
解析:当时,y随x的增大而增大.,当时,y取得最大值,最大值为,即一周可获得的最大利润是1556元.故选B.
2.答案:A
解析:设,则,根据题意,得,所以当时,取得最小值,此时,是的中点.故选A.
3.答案:A
解析:当时,;
当时,;
当时,.
符合题意的图象是选项A中的图象.
故选A.
4.答案:C
解析:本题考查二次函数的实际应用.由题意知,当时,取最大值为,故选C.
5.答案:B
解析:设降价x元时获取利润y元,则有.,当时,.
6.答案:A
解析:抛物线的顶点坐标为,可设抛物线的函数解析式为.篮圈中心在抛物线上,将其代入上式,得,,.由题图知,篮圈中心的坐标是,抛物线的顶点坐标是.设这次跳投时,球出手处离地面h m,,当时,.这次跳投时,球出手处离地面2.25m.故选A.
7.答案:B
解析:抛物线顶点D的坐标为点B的横坐标为,把代入,得.故选B.
8.答案:C
解析:将图象中的三个点、、代入函数关系中,得.解得.函数关系式为.加工煎炸臭豆腐的最佳时间为分钟.故选C.
9.答案:D
解析:如答图,过点D作于点E,,,得矩形面积当时,S有最大值,此时.故选D.
10.答案:25
解析:设利润为w元,则,,当时,w有最大值25.
11.答案:2.25
解析:以水池中心为原点,竖直安装的水管AB所在的直线为y轴,与水管垂直的直线为x轴建立平面直角坐标系.由于在距水池中心的水平距离为1 m时达到最高,高度为3 m,则设抛物线对应的函数表达式为,将代入,得,解得抛物线对应的函数表达式为.令,则,即水管AB的长为2.25 m.
12.答案:
解析:建立平面直角坐标系,设横轴x经过A,B,纵轴y通过AB中点O且经过C点,通过画图可知,抛物线以y轴为对称轴,且经过A,B两点,OA和OB为AB的一半2m,抛物线顶点C的坐标为,通过以上条件可设抛物线的顶点式为,代入A点坐标,得出.所以抛物线的解析式为.当水面下降2m,即当时,有,解得,所以水面宽度增加到米,比原先的宽度增加了m.
13.答案:(1),抛物线的顶点为最低点,
,
绳子最低点离地面的距离为米.
(2)由(1)可知,,令,得,,.
由题意得抛物线的顶点坐标为,
设的解析式为,
将代入,得,解得,
抛物线的解析式为.
当时,,
MN的长度为2.1米.
(3),根据抛物线的对称性可知抛物线的顶点在线段ND的垂直平分线上,
抛物线的顶点坐标为,
抛物线的解析式为.
把代入,得,
,.
k是关于m的二次函数.
又,k随m的增大而增大.
当时,,解得,(不符合题意,舍去).
当时,,解得,(不符合题意,舍去).
m的取值范围是.
一、单选题
1.便民商店经营一种商品,在销售过程中发现一周所获利润y(元)与每件销售价x(元)之间满足关系式,由于某种原因,价格只能满足,那么一周可获得的最大利润是( )
A.1554元 B.1556元 C.1558元 D.1560元
2.如图,点是线段上的一动点,,分别以和为一边作正方形,用表示这两个正方形的面积之和,下列判断正确的是( )
A.当是的中点时,最小 B.当是的中点时,最大
C.当是的三等分点时,最小 D.当是的三等分点时,最大
3.如图,矩形中,,,点从出发,以每秒2个单位沿运动,同时点也从出发,以每秒1个单位沿运动,的面积为,运动的时间为秒,则关于的函数图象为( )
A. B. C. D.
4.竖直上抛物体离地面的高度与运动时间之间的关系可以近似地用公式表示,其中是物体抛出时离地面的高度,是物体抛出时的速度.某人将一个小球从距地面的高处以的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A. B. C. D.
5.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,则能获取的最大利润是( )
A.600元 B.625元 C.650元 D.675元
6.一位篮球运动员在距篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动到与球出手处水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面的高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是 B.篮圈中心的坐标是
C.此抛物线的顶点坐标是 D.篮球出手时离地面的高度是2m
7.小明以二次函数的图像为灵感设计了一款杯子,如图为杯子的设计稿,若,则杯子的高CE为( )
A.14 B.11 C.6 D.3
8.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不煳”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”p与加工煎炸时间t(单位:分钟)近似满足的函数关系为(,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
9.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中的方法从这些边角料上截取矩形(阴影部分)片备用,当截取的矩形面积最大时,矩形两边长x,y分别为( )
A. B. C. D.
二、填空题
10.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(,且x为整数)出售,可卖出件.若使利润最大,则每件商品的售价应为__________元.
11.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与水池中心A的水平距离为1 m处达到最高点C,高度为3 m,水柱落地点D离水池中心A处3 m,则水管AB的长为__________m.
12.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加_________m.
三、解答题
13.如图①,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线的绳子.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图②),使左边抛物线的最低点距MN1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线对应函数的二次项系数始终为.设MN离AB的距离为m,抛物线的顶点离地面的距离为k,当时,求m的取值范围.
参考答案
1.答案:B
解析:当时,y随x的增大而增大.,当时,y取得最大值,最大值为,即一周可获得的最大利润是1556元.故选B.
2.答案:A
解析:设,则,根据题意,得,所以当时,取得最小值,此时,是的中点.故选A.
3.答案:A
解析:当时,;
当时,;
当时,.
符合题意的图象是选项A中的图象.
故选A.
4.答案:C
解析:本题考查二次函数的实际应用.由题意知,当时,取最大值为,故选C.
5.答案:B
解析:设降价x元时获取利润y元,则有.,当时,.
6.答案:A
解析:抛物线的顶点坐标为,可设抛物线的函数解析式为.篮圈中心在抛物线上,将其代入上式,得,,.由题图知,篮圈中心的坐标是,抛物线的顶点坐标是.设这次跳投时,球出手处离地面h m,,当时,.这次跳投时,球出手处离地面2.25m.故选A.
7.答案:B
解析:抛物线顶点D的坐标为点B的横坐标为,把代入,得.故选B.
8.答案:C
解析:将图象中的三个点、、代入函数关系中,得.解得.函数关系式为.加工煎炸臭豆腐的最佳时间为分钟.故选C.
9.答案:D
解析:如答图,过点D作于点E,,,得矩形面积当时,S有最大值,此时.故选D.
10.答案:25
解析:设利润为w元,则,,当时,w有最大值25.
11.答案:2.25
解析:以水池中心为原点,竖直安装的水管AB所在的直线为y轴,与水管垂直的直线为x轴建立平面直角坐标系.由于在距水池中心的水平距离为1 m时达到最高,高度为3 m,则设抛物线对应的函数表达式为,将代入,得,解得抛物线对应的函数表达式为.令,则,即水管AB的长为2.25 m.
12.答案:
解析:建立平面直角坐标系,设横轴x经过A,B,纵轴y通过AB中点O且经过C点,通过画图可知,抛物线以y轴为对称轴,且经过A,B两点,OA和OB为AB的一半2m,抛物线顶点C的坐标为,通过以上条件可设抛物线的顶点式为,代入A点坐标,得出.所以抛物线的解析式为.当水面下降2m,即当时,有,解得,所以水面宽度增加到米,比原先的宽度增加了m.
13.答案:(1),抛物线的顶点为最低点,
,
绳子最低点离地面的距离为米.
(2)由(1)可知,,令,得,,.
由题意得抛物线的顶点坐标为,
设的解析式为,
将代入,得,解得,
抛物线的解析式为.
当时,,
MN的长度为2.1米.
(3),根据抛物线的对称性可知抛物线的顶点在线段ND的垂直平分线上,
抛物线的顶点坐标为,
抛物线的解析式为.
把代入,得,
,.
k是关于m的二次函数.
又,k随m的增大而增大.
当时,,解得,(不符合题意,舍去).
当时,,解得,(不符合题意,舍去).
m的取值范围是.
