山东省潍坊市2021-2022学年高二上学期期中考试数学试题(PDF版含答案)
文档属性
| 名称 | 山东省潍坊市2021-2022学年高二上学期期中考试数学试题(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 728.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 21:30:44 | ||
图片预览



文档简介
2021年11月份期中检测试题
高 二 数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试用时120分钟。
注意事项:
1.答题前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号、班级和科类填写在答
题卡和答题纸规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改
动,用橡皮擦干净后,再选涂其它答案标号。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应
的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改
液、胶带纸、修正带。不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
第Ⅰ卷(共60分)
一、单项选择题:本大题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合
题目要求的.
1.直线x+y+1=0的倾斜角为
A.π 3π π4 B.4 C.3 D.
2π
3
2.已知直线l不在平面α内,则“l∥α”是“直线l上存在两个点到平面α的距离相等”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.在平面直角坐标系中,直线 3x-y+3=0绕它与x 轴的交点A 按顺时针方向旋转
30°所得的直线方程是
A.x-3y-3=0 B.x=3
C.x-3y+3=0 D.x-3y+33=0
4.若直线ax+2y+2=0与直线3x-y-2=0垂直,则a=
A.-23 B.-6 C.
3
2 D.
2
3
5.半径为4的半圆卷成一个圆锥,则该圆锥的体积为
A.23π3 B.
43π
3 C.
83π
3 D.
163π
3
高二数学试题第1页(共4页)
6.圆C 上的点(1,2)关于直线x+y=0的对称点仍在圆C 上,且该圆的半径为 5,则圆
C 的方程为
A.x2+y2=5 B.(x+1)2+(y-1)2=5
C.x2+y2=5或(x-1)2+(y+1)2=5 D.x2+y2=5或(x+1)2+(y-1)2=5
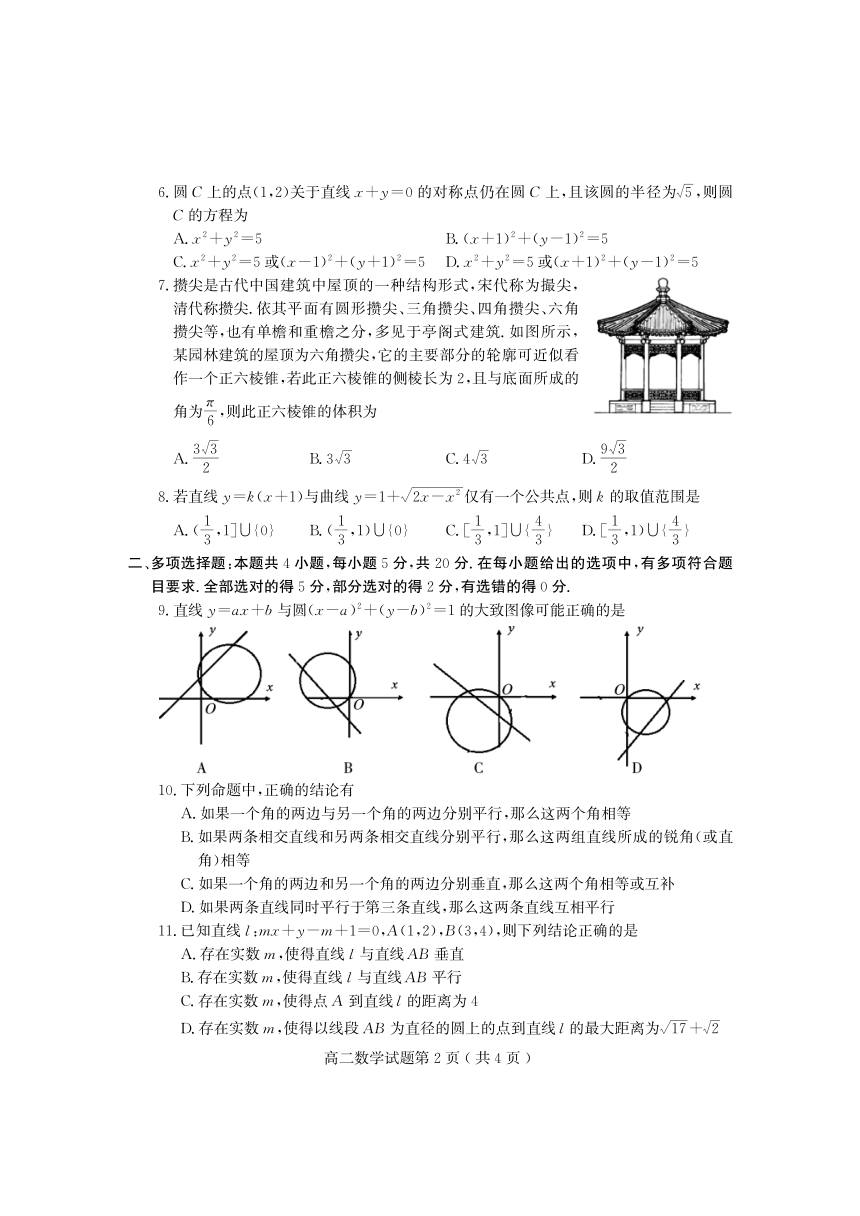
7.攒尖是古代中国建筑中屋顶的一种结构形式,宋代称为撮尖,
清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、六角
攒尖等,也有单檐和重檐之分,多见于亭阁式建筑.如图所示,
某园林建筑的屋顶为六角攒尖,它的主要部分的轮廓可近似看
作一个正六棱锥,若此正六棱锥的侧棱长为2,且与底面所成的
角为π,则此正六棱锥的体积为
6
A.332 B.33 C.43 D.
93
2
8.若直线y=k(x+1)与曲线y=1+ 2x-x2仅有一个公共点,则k的取值范围是
A.(1,1]∪{0} B.(1,1)∪{0} C.[1,1]∪{4} D.[1,1)3 3 3 3 3 ∪
{4}
3
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.直线y=ax+b与圆(x-a)2+(y-b)2=1的大致图像可能正确的是
10.下列命题中,正确的结论有
A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等
B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直
角)相等
C.如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行
11.已知直线l:mx+y-m+1=0,A(1,2),B(3,4),则下列结论正确的是
A.存在实数m,使得直线l与直线AB 垂直
B.存在实数m,使得直线l与直线AB 平行
C.存在实数m,使得点A 到直线l的距离为4
D.存在实数m,使得以线段AB 为直径的圆上的点到直线l的最大距离为 17+2
高二数学试题第2页(共4页)
12.“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面
体,它体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三
棱锥,共截去八个三棱锥,得到的半正多面体的表面积为12+43,则关于该半正多面
体的下列说法中正确的是
A.AB=2
B.该半正多面体的外接球的表面积为6π
C.AB 与平面BCD 所成的角为π4
D.与AB 所成的角是π的棱共有3 16
条
第Ⅱ卷(非选择题,共90分)
三、填空题:(本大题共4小题,每小题5分,共20分,把正确答案填在答题卡相应题的横线上)
13.过P(1,2),Q(-2,1)两点的直线l的斜率为 .
→ → → →
14.已知空间向量m=(-1,x,2),n=(1,3,y),若m∥n,则x+y= .
15.过点 P(1,3),Q(0,a)的光线经 y 轴反射后与圆x2+y2=1相切,则a
= .
16.已知点P(1,2,3)是空间直角坐标系O-xyz内一点,则点P 关于x轴的对称点Q 的
坐标为 .若点 P 在平面xOy 上的射影为 M,则四面体O-PQM 的体积
为 .
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知△ABC 的三个顶点A(4,0),B(8,10),C(0,a),边AC 的中线所在直线方程
为4x-3y-2=0,
(1)求实数a;
(2)试判断点C 与以线段AB 为直径的圆的位置关系,并说明理由.
18.(本小题满分12分)
→ →
如图,三棱柱ABC-A1B1C1中,D 为B1C1的中点,A1E=ED,设
→ → → → → →
AA1=a,AB=b,AC=c.
(1)
→,→试用ab,
→ →
c表示向量AE;
(2)若∠A1AB=∠A1AC=60°,∠CAB=90°,A1A=AC=AB=2,
求异面直线AE 与BB1所成角的余弦值.
高二数学试题第3页(共4页)
19.(本小题满分12分)
如图,在五面体ABCDEF 中,四边形ABCD 是矩形,AB//EF,AB=2EF,∠EAB=90°,
平面ABFE⊥平面ABCD.
(1)若点G 是AC 的中点,求证:FG//平面AED;
(2)若AE=AD=1,AB=2,求点D 到平面AFC 的距离.
20.(本小题满分12分)
已知圆C 的圆心在直线y=2x-1上,且过点A(1,3),B(2,2).
(1)求圆C 的方程;
(2)已知圆C 上存在点M,使得△MAB 的面积为1,求点M 的坐标2 .
21.(本小题满分12分)
如图,已知矩形ABCD 中,AB=4,AD=2,
M 为DC 的中点,将△ADM 沿AM 折起,使得平
面ADM⊥平面ABCM.
(1)求证:平面ADM⊥平面BDM;
(2)若点E 是线段DB 上的一动点,且DE=tDB(0弦值为 5时,求
5 t
的值.
22.(本小题满分12分)
已知圆M 的圆心与点N(-1,4)关于直线x-y+1=0对称,且圆M 与y 轴相切于原
点O.
(1)求圆M 的方程;
(2)过原点O 的两条直线与圆M 分别交于A,B 两点,直线OA,OB 的斜率之积为-1,2
OD⊥AB,D 为垂足,是否存在定点P,使得|DP|为定值,若存在,求出P 点坐标;若不存在,
说明理由.
高二数学试题第4页(共4页)
高二数学试题参考答案及评分标准
一、单项选择题:本大题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合
题目要求的.
1-5BACDC 6-8DAD
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.AC 10.BD 11.ABD 12.ACD
三、填空题:(本大题共4小题,每小题5分,共20分,把正确答案填在答题卡相应题的横线上)
13.13 14.-5 15.
5 (, , )
3 16.1-2-3 2
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.解:(1)由题意可得,AC 的中点坐标为D(2,a),…………………………………2分2
所以4×2-3×a ,……………………………………………………………… 分2-2=0 4
所以a=4; ………………………………………………………………………………5分
(2)由已知可得AB 的中点坐标为(6,5),………………………………………………6分
得|AB|= (8-4)2+102=2 29,……………………………………………………7分
所以以AB 为直径的圆的方程为(x-6)2+(y-5)2=29,
因为(0-6)2+(4-5)2=37>29,………………………………………………………9分
所以点C 在以AB 为直径的圆外 .……………………………………………………10分
18.解:(1)因为D 为B1C1中点,
→
所以A1D=
1(→ → → →
2 A1B1+A1C
1
1)= (2b+c
), …………………………………………2分
→ → → 1 → 1 → → 由A1E=ED,所以A1E= A1D= (b+c),………………………………………4分2 4
→ → → → 1(→ →所以AE=AA1+A1E=a+ b+c);………………………………………………4 5
分
(2)
→ → → →
由题意知a·b=2×2×cos60°=2,a·c=2×2×cos60°=2,
→
b·
→
c=2×2×cos90°=0, ………………………………………………………………7分
→ → → → → →
所以|AE|=|AA1+AE|= [a+
1(b+c)]2= 261 ,4 2
→
|BB1|=2,
→ → → → → →
AE·BB 11=[a+ (b+c)]·a=5,…………………………………………………… 分4 9
→ →
<→ → AE
·
, > BB所以cosAE BB = 1 =5 261 ,………………………………………… 分→ → 26 11
|AE||BB1|
所以异面直线AE 与BC1所成角的余弦值为
5 26. ………………………………12分26
高二数学试题参考答案第1页(共4页)
19.证明:(1)取AD 中点H,连接EH,GH,
因为H,G 分别为AD,AC 的中点,
所以GH∥DC,且GH=1DC,………………………………2 2
分
因为四边形ABCD 是矩形,AB//EF,AB=2EF,
所以EF∥DC,且EF=12DC
,
所以GH=EF,且GH∥EF,
所以四边形EFGH 是平行四边形,……………………………………………………4分
所以FG∥EH,
又FG 平面AED,EH 平面AED,
所以FG∥平面AED;……………………………………………………………………6分
(2)证明:因为平面ABFE⊥平面ABCD,
平面ABFE∩平面ABCD=AB,AE⊥AB,AE 平面ABEF,
所以AE⊥平面ABCD.…………………………………………………………………7分
因为EF//AB,EF 平面ABCD,AB 平面ABCD,
所以EF//平面ABCD …………………………………………………………………8分
所以F 到平面ACD 的距离为E 到平面ACD 的距离EA,
所以V三棱锥D-AFC=V三棱锥F-ADC,设D 到平面AFC 的距离h,
所以1·
3 S△AFC
·h=1·S△ADC·EA=
1×1×1×2×1=1,…………………… 分3 3 2 3 9
因为AF=2,AC=5,FC=3,
所以AF⊥FC,…………………………………………………………………………10分
所以S =1AF·FC=1×2×3= 6△AFC ,2 2 2
所以h= 1 =1= 6 ……………………………………………………………… 分S△AFC 6 3
11
2
所以点D 到平面AFC 的距离为 6.…………………………………………………12分3
20.解:(1)由题意知AB 所在直线的斜率为kAB=
2-3 ,
2-1=-1
A(1,3),B(2,2)的中点为(3,5),2 2
所以线段AB 的垂直平分线为y-
5 3,
2=x-2
即y=x+1,
,
联立 y=2x-1,,得C(2,3)…………………………………………………………… 分y=x+1 2
半径r= (2-2)2+(3-2)2=1,
所以圆C 方程为(x-2)2+(y-3)2=1;………………………………………………4分
(2)由题意得AB 所在直线方程为y-2=-(x-2),即x+y-4=0,………………5分
高二数学试题参考答案第2页(共4页)
可得|AB|=2,
因为三角形MAB 的面积为1,2
所以点M 到直线AB 的距离为 2,……………………………………………………8分2
设点M 所在直线方程为x+y+c=0,
所以d=|c+4|= 2,
2 2
所以c=-3或-5,………………………………………………………………………9分
( )2 ( )2 ,
当c=-3时,联立 x-2 +y-3 =1x+y-3=0,
无解;
(x-2)2 (当c=-5时,联立 +y-3)
2=1,
x+y-5=0,
2, x=2+2 x=2-
2,
得 或 2
2 2
y=3-
, y=3+ ,2 2
所以M(2+ 2,3- 2)或M(2- 2,2 2 2 3+
2).……………………………………… 分2 12
21.证明:(1)因为在矩形ABCD 中,AB=4,AD=2,M 为DC 的中点,
所以AM=BM=22,
因为AM2+BM2=AB2,所以AM⊥BM,……………………………………………1分
因为平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,
BM 平面ABCM,
所以BM⊥平面ADM,…………………………………………………………………3分
因为AD 平面ADM,所以AD⊥BM,………………………………………………4分
又因为AD⊥DM,DM∩BM=M,所以AD⊥平面BDM,…………………………5分
又因为AD 平面ADM,
所以平面ADM⊥平面BDM; …………………………………………………………6分
(2)解:取AM 中点O,连接DO,则DO⊥平面ABCM,过O 做AM 的垂线,交AB 于
点F,
以O 为原点,OA,OF,OD 所在直线分别为x,y,z轴,建立如图所示空间直角坐标系,
………………………………………………………………………………………………7分
则A(2,0,0),B(-2,22,0),
M(-2,0,0),D(0,0,2),
→
平面ADM 的一个法向量为n1=(0,1,0),………………8分
→ →
因为DE=tDB 且0→ → → → →
ME=MD+DE=MD+tDB=(2-2t,22t,2-2t),
高二数学试题参考答案第3页(共4页)
→
AM=(-22,0,0),……………………………………………………………………9分
→·→
→ n2 AM=0,
设平面AME 的一个法向量为n2=(x,y,z) 则 →n2·→ME=0,
即 -22x=0,(2-2t)x+22ty+(2-2t)z=0,
→
取y=1,得n2=(0,1,
2t ),…………………………………………………………10分t-1
→· →
所以cos<
→,→n n >
n n
= 1 21 2 → → =
1 = 5,
|n1||n 52| 1+(2t )2t-1
解得t=1,所以t=1 …………………………………………………………………12分2 2
22.解:(1)设M(a,b),
b-4=-1,
则 a+1 ………………………………………………………………… 分a-1 b+4 2 - , 2 2 +1=0
,
解得 a=3,………………………………………………………………………………b=0 3分
所以该圆的半径为3,……………………………………………………………………4分
所以圆M 的方程为(x-3)2+y2=9;…………………………………………………5分
(2)由题意知圆M 的方程为(x-3)2+y2=9,…………………………………………6分
设OA 所在直线方程为y=kx(k≠0),
( )2 2 ,
联立 x-3 +y =9y=kx,
得x 6A= 2,yA=
6k , …………………………………………………………… 分
1+k 1+k2 8
2
同理把k换做-1,可得x = 24k , =-12kB 2yB 2,…………………………………2k 1+4k 1+4k 9
分
所以AB 所在直线方程为 - 6k 3k ( 6y ),………………………… 分1+k2=1-2k2x-1+k2 10
当y=0时,可得x=4,
故直线AB 过定点C(4,0),……………………………………………………………11分
由于OC 为定值,且△ODC 为直角三角形,OC 为斜边,
所以OC 中点P 满足|DP|=|OC|2 =2
为定值,
由于O(0,0),C(4,0),故由中点坐标公式可得P(2,0),
故存在点P(2,0),使得|DP|为定值.…………………………………………………12分
高二数学试题参考答案第4页(共4页)
高 二 数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试用时120分钟。
注意事项:
1.答题前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号、班级和科类填写在答
题卡和答题纸规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改
动,用橡皮擦干净后,再选涂其它答案标号。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应
的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改
液、胶带纸、修正带。不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
第Ⅰ卷(共60分)
一、单项选择题:本大题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合
题目要求的.
1.直线x+y+1=0的倾斜角为
A.π 3π π4 B.4 C.3 D.
2π
3
2.已知直线l不在平面α内,则“l∥α”是“直线l上存在两个点到平面α的距离相等”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.在平面直角坐标系中,直线 3x-y+3=0绕它与x 轴的交点A 按顺时针方向旋转
30°所得的直线方程是
A.x-3y-3=0 B.x=3
C.x-3y+3=0 D.x-3y+33=0
4.若直线ax+2y+2=0与直线3x-y-2=0垂直,则a=
A.-23 B.-6 C.
3
2 D.
2
3
5.半径为4的半圆卷成一个圆锥,则该圆锥的体积为
A.23π3 B.
43π
3 C.
83π
3 D.
163π
3
高二数学试题第1页(共4页)
6.圆C 上的点(1,2)关于直线x+y=0的对称点仍在圆C 上,且该圆的半径为 5,则圆
C 的方程为
A.x2+y2=5 B.(x+1)2+(y-1)2=5
C.x2+y2=5或(x-1)2+(y+1)2=5 D.x2+y2=5或(x+1)2+(y-1)2=5
7.攒尖是古代中国建筑中屋顶的一种结构形式,宋代称为撮尖,
清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、六角
攒尖等,也有单檐和重檐之分,多见于亭阁式建筑.如图所示,
某园林建筑的屋顶为六角攒尖,它的主要部分的轮廓可近似看
作一个正六棱锥,若此正六棱锥的侧棱长为2,且与底面所成的
角为π,则此正六棱锥的体积为
6
A.332 B.33 C.43 D.
93
2
8.若直线y=k(x+1)与曲线y=1+ 2x-x2仅有一个公共点,则k的取值范围是
A.(1,1]∪{0} B.(1,1)∪{0} C.[1,1]∪{4} D.[1,1)3 3 3 3 3 ∪
{4}
3
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.直线y=ax+b与圆(x-a)2+(y-b)2=1的大致图像可能正确的是
10.下列命题中,正确的结论有
A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等
B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直
角)相等
C.如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行
11.已知直线l:mx+y-m+1=0,A(1,2),B(3,4),则下列结论正确的是
A.存在实数m,使得直线l与直线AB 垂直
B.存在实数m,使得直线l与直线AB 平行
C.存在实数m,使得点A 到直线l的距离为4
D.存在实数m,使得以线段AB 为直径的圆上的点到直线l的最大距离为 17+2
高二数学试题第2页(共4页)
12.“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面
体,它体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三
棱锥,共截去八个三棱锥,得到的半正多面体的表面积为12+43,则关于该半正多面
体的下列说法中正确的是
A.AB=2
B.该半正多面体的外接球的表面积为6π
C.AB 与平面BCD 所成的角为π4
D.与AB 所成的角是π的棱共有3 16
条
第Ⅱ卷(非选择题,共90分)
三、填空题:(本大题共4小题,每小题5分,共20分,把正确答案填在答题卡相应题的横线上)
13.过P(1,2),Q(-2,1)两点的直线l的斜率为 .
→ → → →
14.已知空间向量m=(-1,x,2),n=(1,3,y),若m∥n,则x+y= .
15.过点 P(1,3),Q(0,a)的光线经 y 轴反射后与圆x2+y2=1相切,则a
= .
16.已知点P(1,2,3)是空间直角坐标系O-xyz内一点,则点P 关于x轴的对称点Q 的
坐标为 .若点 P 在平面xOy 上的射影为 M,则四面体O-PQM 的体积
为 .
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知△ABC 的三个顶点A(4,0),B(8,10),C(0,a),边AC 的中线所在直线方程
为4x-3y-2=0,
(1)求实数a;
(2)试判断点C 与以线段AB 为直径的圆的位置关系,并说明理由.
18.(本小题满分12分)
→ →
如图,三棱柱ABC-A1B1C1中,D 为B1C1的中点,A1E=ED,设
→ → → → → →
AA1=a,AB=b,AC=c.
(1)
→,→试用ab,
→ →
c表示向量AE;
(2)若∠A1AB=∠A1AC=60°,∠CAB=90°,A1A=AC=AB=2,
求异面直线AE 与BB1所成角的余弦值.
高二数学试题第3页(共4页)
19.(本小题满分12分)
如图,在五面体ABCDEF 中,四边形ABCD 是矩形,AB//EF,AB=2EF,∠EAB=90°,
平面ABFE⊥平面ABCD.
(1)若点G 是AC 的中点,求证:FG//平面AED;
(2)若AE=AD=1,AB=2,求点D 到平面AFC 的距离.
20.(本小题满分12分)
已知圆C 的圆心在直线y=2x-1上,且过点A(1,3),B(2,2).
(1)求圆C 的方程;
(2)已知圆C 上存在点M,使得△MAB 的面积为1,求点M 的坐标2 .
21.(本小题满分12分)
如图,已知矩形ABCD 中,AB=4,AD=2,
M 为DC 的中点,将△ADM 沿AM 折起,使得平
面ADM⊥平面ABCM.
(1)求证:平面ADM⊥平面BDM;
(2)若点E 是线段DB 上的一动点,且DE=tDB(0
5 t
的值.
22.(本小题满分12分)
已知圆M 的圆心与点N(-1,4)关于直线x-y+1=0对称,且圆M 与y 轴相切于原
点O.
(1)求圆M 的方程;
(2)过原点O 的两条直线与圆M 分别交于A,B 两点,直线OA,OB 的斜率之积为-1,2
OD⊥AB,D 为垂足,是否存在定点P,使得|DP|为定值,若存在,求出P 点坐标;若不存在,
说明理由.
高二数学试题第4页(共4页)
高二数学试题参考答案及评分标准
一、单项选择题:本大题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合
题目要求的.
1-5BACDC 6-8DAD
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.AC 10.BD 11.ABD 12.ACD
三、填空题:(本大题共4小题,每小题5分,共20分,把正确答案填在答题卡相应题的横线上)
13.13 14.-5 15.
5 (, , )
3 16.1-2-3 2
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.解:(1)由题意可得,AC 的中点坐标为D(2,a),…………………………………2分2
所以4×2-3×a ,……………………………………………………………… 分2-2=0 4
所以a=4; ………………………………………………………………………………5分
(2)由已知可得AB 的中点坐标为(6,5),………………………………………………6分
得|AB|= (8-4)2+102=2 29,……………………………………………………7分
所以以AB 为直径的圆的方程为(x-6)2+(y-5)2=29,
因为(0-6)2+(4-5)2=37>29,………………………………………………………9分
所以点C 在以AB 为直径的圆外 .……………………………………………………10分
18.解:(1)因为D 为B1C1中点,
→
所以A1D=
1(→ → → →
2 A1B1+A1C
1
1)= (2b+c
), …………………………………………2分
→ → → 1 → 1 → → 由A1E=ED,所以A1E= A1D= (b+c),………………………………………4分2 4
→ → → → 1(→ →所以AE=AA1+A1E=a+ b+c);………………………………………………4 5
分
(2)
→ → → →
由题意知a·b=2×2×cos60°=2,a·c=2×2×cos60°=2,
→
b·
→
c=2×2×cos90°=0, ………………………………………………………………7分
→ → → → → →
所以|AE|=|AA1+AE|= [a+
1(b+c)]2= 261 ,4 2
→
|BB1|=2,
→ → → → → →
AE·BB 11=[a+ (b+c)]·a=5,…………………………………………………… 分4 9
→ →
<→ → AE
·
, > BB所以cosAE BB = 1 =5 261 ,………………………………………… 分→ → 26 11
|AE||BB1|
所以异面直线AE 与BC1所成角的余弦值为
5 26. ………………………………12分26
高二数学试题参考答案第1页(共4页)
19.证明:(1)取AD 中点H,连接EH,GH,
因为H,G 分别为AD,AC 的中点,
所以GH∥DC,且GH=1DC,………………………………2 2
分
因为四边形ABCD 是矩形,AB//EF,AB=2EF,
所以EF∥DC,且EF=12DC
,
所以GH=EF,且GH∥EF,
所以四边形EFGH 是平行四边形,……………………………………………………4分
所以FG∥EH,
又FG 平面AED,EH 平面AED,
所以FG∥平面AED;……………………………………………………………………6分
(2)证明:因为平面ABFE⊥平面ABCD,
平面ABFE∩平面ABCD=AB,AE⊥AB,AE 平面ABEF,
所以AE⊥平面ABCD.…………………………………………………………………7分
因为EF//AB,EF 平面ABCD,AB 平面ABCD,
所以EF//平面ABCD …………………………………………………………………8分
所以F 到平面ACD 的距离为E 到平面ACD 的距离EA,
所以V三棱锥D-AFC=V三棱锥F-ADC,设D 到平面AFC 的距离h,
所以1·
3 S△AFC
·h=1·S△ADC·EA=
1×1×1×2×1=1,…………………… 分3 3 2 3 9
因为AF=2,AC=5,FC=3,
所以AF⊥FC,…………………………………………………………………………10分
所以S =1AF·FC=1×2×3= 6△AFC ,2 2 2
所以h= 1 =1= 6 ……………………………………………………………… 分S△AFC 6 3
11
2
所以点D 到平面AFC 的距离为 6.…………………………………………………12分3
20.解:(1)由题意知AB 所在直线的斜率为kAB=
2-3 ,
2-1=-1
A(1,3),B(2,2)的中点为(3,5),2 2
所以线段AB 的垂直平分线为y-
5 3,
2=x-2
即y=x+1,
,
联立 y=2x-1,,得C(2,3)…………………………………………………………… 分y=x+1 2
半径r= (2-2)2+(3-2)2=1,
所以圆C 方程为(x-2)2+(y-3)2=1;………………………………………………4分
(2)由题意得AB 所在直线方程为y-2=-(x-2),即x+y-4=0,………………5分
高二数学试题参考答案第2页(共4页)
可得|AB|=2,
因为三角形MAB 的面积为1,2
所以点M 到直线AB 的距离为 2,……………………………………………………8分2
设点M 所在直线方程为x+y+c=0,
所以d=|c+4|= 2,
2 2
所以c=-3或-5,………………………………………………………………………9分
( )2 ( )2 ,
当c=-3时,联立 x-2 +y-3 =1x+y-3=0,
无解;
(x-2)2 (当c=-5时,联立 +y-3)
2=1,
x+y-5=0,
2, x=2+2 x=2-
2,
得 或 2
2 2
y=3-
, y=3+ ,2 2
所以M(2+ 2,3- 2)或M(2- 2,2 2 2 3+
2).……………………………………… 分2 12
21.证明:(1)因为在矩形ABCD 中,AB=4,AD=2,M 为DC 的中点,
所以AM=BM=22,
因为AM2+BM2=AB2,所以AM⊥BM,……………………………………………1分
因为平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,
BM 平面ABCM,
所以BM⊥平面ADM,…………………………………………………………………3分
因为AD 平面ADM,所以AD⊥BM,………………………………………………4分
又因为AD⊥DM,DM∩BM=M,所以AD⊥平面BDM,…………………………5分
又因为AD 平面ADM,
所以平面ADM⊥平面BDM; …………………………………………………………6分
(2)解:取AM 中点O,连接DO,则DO⊥平面ABCM,过O 做AM 的垂线,交AB 于
点F,
以O 为原点,OA,OF,OD 所在直线分别为x,y,z轴,建立如图所示空间直角坐标系,
………………………………………………………………………………………………7分
则A(2,0,0),B(-2,22,0),
M(-2,0,0),D(0,0,2),
→
平面ADM 的一个法向量为n1=(0,1,0),………………8分
→ →
因为DE=tDB 且0
ME=MD+DE=MD+tDB=(2-2t,22t,2-2t),
高二数学试题参考答案第3页(共4页)
→
AM=(-22,0,0),……………………………………………………………………9分
→·→
→ n2 AM=0,
设平面AME 的一个法向量为n2=(x,y,z) 则 →n2·→ME=0,
即 -22x=0,(2-2t)x+22ty+(2-2t)z=0,
→
取y=1,得n2=(0,1,
2t ),…………………………………………………………10分t-1
→· →
所以cos<
→,→n n >
n n
= 1 21 2 → → =
1 = 5,
|n1||n 52| 1+(2t )2t-1
解得t=1,所以t=1 …………………………………………………………………12分2 2
22.解:(1)设M(a,b),
b-4=-1,
则 a+1 ………………………………………………………………… 分a-1 b+4 2 - , 2 2 +1=0
,
解得 a=3,………………………………………………………………………………b=0 3分
所以该圆的半径为3,……………………………………………………………………4分
所以圆M 的方程为(x-3)2+y2=9;…………………………………………………5分
(2)由题意知圆M 的方程为(x-3)2+y2=9,…………………………………………6分
设OA 所在直线方程为y=kx(k≠0),
( )2 2 ,
联立 x-3 +y =9y=kx,
得x 6A= 2,yA=
6k , …………………………………………………………… 分
1+k 1+k2 8
2
同理把k换做-1,可得x = 24k , =-12kB 2yB 2,…………………………………2k 1+4k 1+4k 9
分
所以AB 所在直线方程为 - 6k 3k ( 6y ),………………………… 分1+k2=1-2k2x-1+k2 10
当y=0时,可得x=4,
故直线AB 过定点C(4,0),……………………………………………………………11分
由于OC 为定值,且△ODC 为直角三角形,OC 为斜边,
所以OC 中点P 满足|DP|=|OC|2 =2
为定值,
由于O(0,0),C(4,0),故由中点坐标公式可得P(2,0),
故存在点P(2,0),使得|DP|为定值.…………………………………………………12分
高二数学试题参考答案第4页(共4页)
同课章节目录
