《红对勾》人教版数学必修一1.3.1.1《单调性与最大(小)值》课件
文档属性
| 名称 | 《红对勾》人教版数学必修一1.3.1.1《单调性与最大(小)值》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-19 19:34:53 | ||
图片预览










文档简介
(共48张PPT)
第一章
集合与函数概念
1.3 函数的基本性质
1.3.1 单调性与最大(小)值
第1课时 函数的单调性
1.在回顾初中学过的一次函数、二次函数、反比例函数的图象后,理解函数的单调性的概念.
2.通过取值、描点分析函数值的变化规律,体会函数值的变化趋势,获得形成函数单调性这一概念的经验,探索函数单调性的实质.
研 习 新 知
新 知 视 界
1.增函数
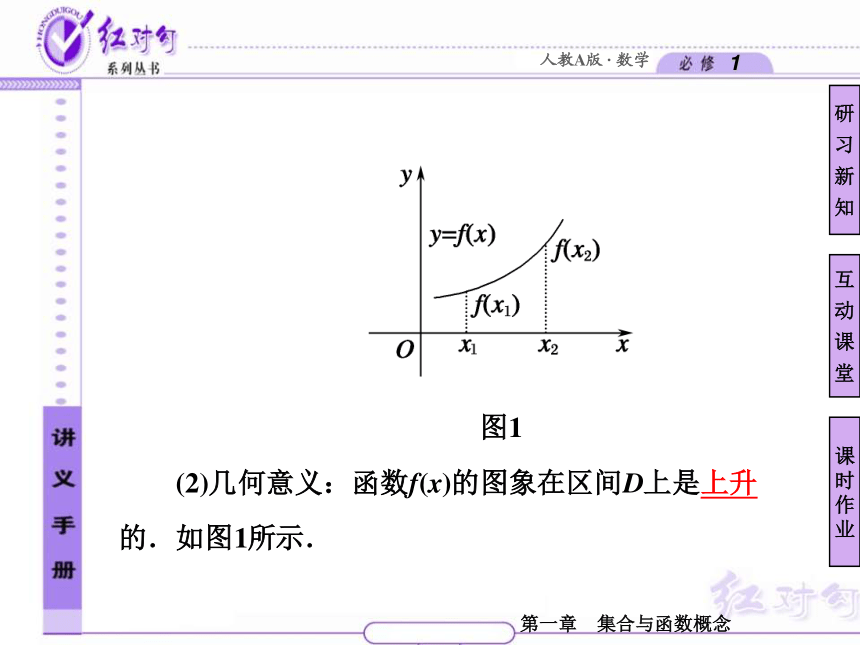
(1)定义:设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x12.减函数
(1)定义:设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x1f(x2),那么就说函数f(x)在区间D上是减函数,区间D称为函数f(x)的单调递减区间.
3.单调性与单调区间
定义:如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
自 我 检 测
1.若函数y=kx+b(k≠0)是R上的减函数,那么( )
A.k>0 B.k<0
C.k≠0 D.无法确定
答案:B
2.函数y=x2在区间[-1,2]上( )
A.是增函数 B.是减函数
C.是增函数又是减函数 D.不具有单调性
答案:D
3.函数y=f(x)的图象如图4所示,其增区间是( )
A.[-4,4]
B.[-4,-3]∪[1,4]
C.[-3,1]
D.[-3,4]
答案:C
4.函数f(x)在(-∞,+∞)上为减函数,则f(-3)与f(2)的大小关系是________.
答案:f(-3)>f(2)
5.求证f(x)=x2-2x在区间(1,+∞)上是增函数.
证明:设x1,x2是区间(1,+∞)上的任意两个值,且x1f(x1)=x12-2x1,f(x2)=x22-2x2,
f(x2)-f(x1)=x22-2x2-x12+2x1
=x22-x12-2x2+2x1
=(x2-x1)(x2+x1)-2(x2-x1)
=(x2-x1)(x2+x1-2).
∵x2>x1,∴x2-x1>0.
又∵x1,x2∈(1,+∞),∴x2>x1>1.
∴x1+x2>2.∴x1+x2-2>0.
∴f(x2)-f(x1)>0,即f(x2)>f(x1).
故f(x)=x2-2x在(1,+∞)上是增函数.
互 动 课 堂
由此可知:y=f(x)的单调增区间是(- ∞,-1],[0,1].
y=f(x)的单调减区间是(-1,0),(1,+∞).
[点评] 利用函数图象确定函数的单调区间,具体做法是:先化简函数式,然后再画出它的草图,最后根据函数定义域与草图的位置、状态,确定函数的单调区间.当单调递增(或递减)区间由几个区间组成时,一般情况下不能取它们的并集,应用“和”或“,”连接.
解:(1)令f(x)=x2+2x-3=(x+1)2-4.先作出f(x)的图象,保留其在x轴及x轴上方部分,把它在x轴下方的图象翻到x轴上方,就得到y=|x2+2x-3|的图象,如图7所示.由图象易得:
递增区间是[-3,-1]和[1,+∞).
递减区间是(-∞,-3]和[-1,1].
类型三 根据单调性求参数取值范围
[例3] 函数f(x)=x2-2ax-3在区间[1,2]上单调,则( )
A.a∈(-∞,1]
B.a∈[2,+∞)
C.a∈[1,2]
D.a∈(-∞,1]∪[2,+∞)
[解析] 本题是关于一个二次函数的单调区间问题.二次函数的单调区间取决于其对称轴,为此需先确定函数的对称轴.
不难得到函数的对称轴为x=a,函数图象开口向上,如图8.
要使函数在区间[1,2]上单调,只需a≤1或a≥2(其中当a≤1时函数在区间[1,2]上单调递增,当a≥2时函数在区间[1,2]上单调递减),从而a∈(-∞,1]∪[2,+∞),故选D.
[答案] D
变式体验3 已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,求实数a的取值范围.
分析:由题意可知是(-∞,4]应该是该函数的递减区间的子区间,从而可通过比较对称轴与4的大小来求得.
解:f(x)=x2+2(a-1)x+2
=[x+(a-1)]2-(a-1)2+2,
∴此二次函数的对称轴为x=1-a,
∴f(x)的单调减区间为(-∞,1-a].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=1-a必须在直线x=4的右侧或与其重合.
∴1-a≥4,解得a≤-3.
类型四 函数单调性的应用
[例4] 已知f(x)是定义在[-1,1]上的增函数,且
f(x-2)[点评] 对于x1思 悟 升 华
1.函数f(x)在给定区间上的单调性,反映了函数f(x)在区间上函数值的变化趋势,是函数的局部性质,所以求函数的单调区间须先求函数的定义域.
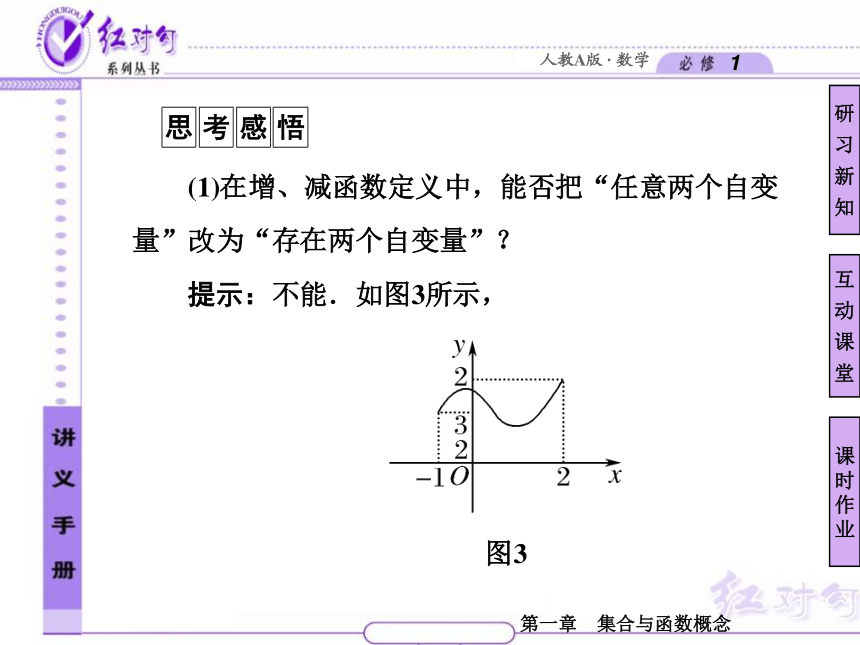
2.函数定义中的x1,x2应深刻理解,一是任意性,即“任意取x1,x2”,“任意”两个字决不能丢掉,不能为某两个特殊值;二是x1,x2有大小,通常规定Δx=x2-x1>0;三是同属于一个单调区间.
3.判断函数的单调性主要是利用定义,其中作差后变形是关键,常采用的方法有因式分解、通分、配方、有理化等.
4.根据函数单调性的定义,若f(x)为增函数,则x1f(x2),它常用来比较大小或解抽象函数的不等式.
课时作业(9)
第一章
集合与函数概念
1.3 函数的基本性质
1.3.1 单调性与最大(小)值
第1课时 函数的单调性
1.在回顾初中学过的一次函数、二次函数、反比例函数的图象后,理解函数的单调性的概念.
2.通过取值、描点分析函数值的变化规律,体会函数值的变化趋势,获得形成函数单调性这一概念的经验,探索函数单调性的实质.
研 习 新 知
新 知 视 界
1.增函数
(1)定义:设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x1
(1)定义:设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x1
3.单调性与单调区间
定义:如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
自 我 检 测
1.若函数y=kx+b(k≠0)是R上的减函数,那么( )
A.k>0 B.k<0
C.k≠0 D.无法确定
答案:B
2.函数y=x2在区间[-1,2]上( )
A.是增函数 B.是减函数
C.是增函数又是减函数 D.不具有单调性
答案:D
3.函数y=f(x)的图象如图4所示,其增区间是( )
A.[-4,4]
B.[-4,-3]∪[1,4]
C.[-3,1]
D.[-3,4]
答案:C
4.函数f(x)在(-∞,+∞)上为减函数,则f(-3)与f(2)的大小关系是________.
答案:f(-3)>f(2)
5.求证f(x)=x2-2x在区间(1,+∞)上是增函数.
证明:设x1,x2是区间(1,+∞)上的任意两个值,且x1
f(x2)-f(x1)=x22-2x2-x12+2x1
=x22-x12-2x2+2x1
=(x2-x1)(x2+x1)-2(x2-x1)
=(x2-x1)(x2+x1-2).
∵x2>x1,∴x2-x1>0.
又∵x1,x2∈(1,+∞),∴x2>x1>1.
∴x1+x2>2.∴x1+x2-2>0.
∴f(x2)-f(x1)>0,即f(x2)>f(x1).
故f(x)=x2-2x在(1,+∞)上是增函数.
互 动 课 堂
由此可知:y=f(x)的单调增区间是(- ∞,-1],[0,1].
y=f(x)的单调减区间是(-1,0),(1,+∞).
[点评] 利用函数图象确定函数的单调区间,具体做法是:先化简函数式,然后再画出它的草图,最后根据函数定义域与草图的位置、状态,确定函数的单调区间.当单调递增(或递减)区间由几个区间组成时,一般情况下不能取它们的并集,应用“和”或“,”连接.
解:(1)令f(x)=x2+2x-3=(x+1)2-4.先作出f(x)的图象,保留其在x轴及x轴上方部分,把它在x轴下方的图象翻到x轴上方,就得到y=|x2+2x-3|的图象,如图7所示.由图象易得:
递增区间是[-3,-1]和[1,+∞).
递减区间是(-∞,-3]和[-1,1].
类型三 根据单调性求参数取值范围
[例3] 函数f(x)=x2-2ax-3在区间[1,2]上单调,则( )
A.a∈(-∞,1]
B.a∈[2,+∞)
C.a∈[1,2]
D.a∈(-∞,1]∪[2,+∞)
[解析] 本题是关于一个二次函数的单调区间问题.二次函数的单调区间取决于其对称轴,为此需先确定函数的对称轴.
不难得到函数的对称轴为x=a,函数图象开口向上,如图8.
要使函数在区间[1,2]上单调,只需a≤1或a≥2(其中当a≤1时函数在区间[1,2]上单调递增,当a≥2时函数在区间[1,2]上单调递减),从而a∈(-∞,1]∪[2,+∞),故选D.
[答案] D
变式体验3 已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,求实数a的取值范围.
分析:由题意可知是(-∞,4]应该是该函数的递减区间的子区间,从而可通过比较对称轴与4的大小来求得.
解:f(x)=x2+2(a-1)x+2
=[x+(a-1)]2-(a-1)2+2,
∴此二次函数的对称轴为x=1-a,
∴f(x)的单调减区间为(-∞,1-a].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=1-a必须在直线x=4的右侧或与其重合.
∴1-a≥4,解得a≤-3.
类型四 函数单调性的应用
[例4] 已知f(x)是定义在[-1,1]上的增函数,且
f(x-2)
1.函数f(x)在给定区间上的单调性,反映了函数f(x)在区间上函数值的变化趋势,是函数的局部性质,所以求函数的单调区间须先求函数的定义域.
2.函数定义中的x1,x2应深刻理解,一是任意性,即“任意取x1,x2”,“任意”两个字决不能丢掉,不能为某两个特殊值;二是x1,x2有大小,通常规定Δx=x2-x1>0;三是同属于一个单调区间.
3.判断函数的单调性主要是利用定义,其中作差后变形是关键,常采用的方法有因式分解、通分、配方、有理化等.
4.根据函数单调性的定义,若f(x)为增函数,则x1
课时作业(9)
