《红对勾》人教版数学必修一1.3.2《集合的基本运算》课件.
文档属性
| 名称 | 《红对勾》人教版数学必修一1.3.2《集合的基本运算》课件. |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-19 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
第一章
集合与函数概念
1.1 集合
1.1.3 集合的基本运算
第2课时
补集及集合的综合应用
1.理解在给定集合中一个子集的补集的含义与性质是本节的重点,一定要重点掌握.
2.并集、交集、补集的运算以及利用Venn图表达集合的关系与运算是考试的重点又是难点,在学习时要用心哦.
研 习 新 知
新 知 视 界
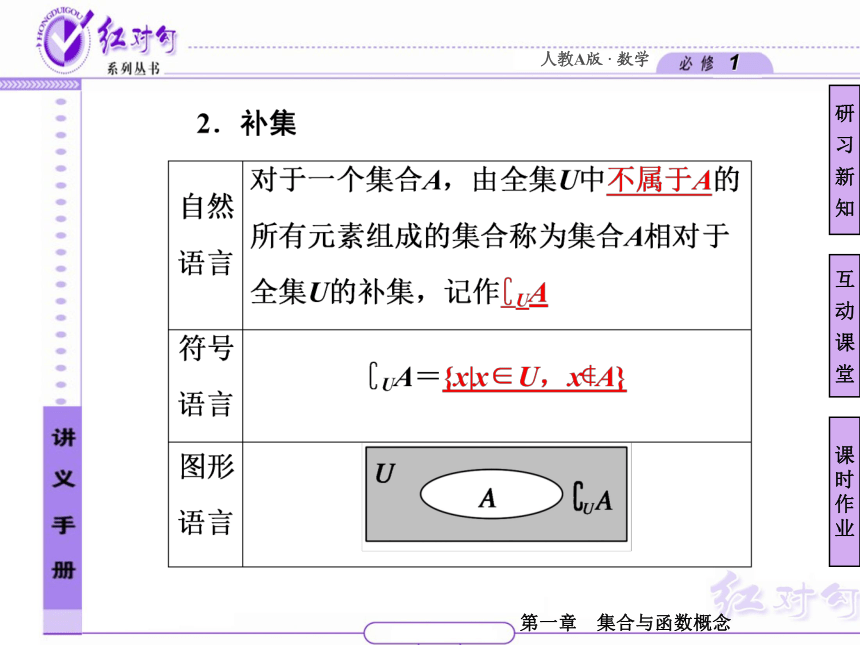
1.全集
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,我们就称这个集合为全集,记作U.
3.补集的性质
(1) U =U;
(2) UU= ;
(3) U( UA)=A;
(4)A∩( UA)= ,A∪( UA)=U;
(5)( UA)∪( UB)= U(A∩B).
自 我 检 测
1.设全集U={1,2,4,8},B={2,4},则 UB=( )
A.{1} B.{8}
C.{1,8} D.
答案:C
2.已知全集U={0,1,2},且 UA={2},则集合A的真子集共有( )
A.3个 B.4个
C.5个 D.6个
解析:∵U={0,1,2},且 UA={2},
∴A={0,1}.∴A的真子集是{0},{1}, 共3个,故选A.
答案:A
3.设集合S={三角形},A={直角三角形},则 SA=__________.
解析:三角形中去掉直角三角形,∴ SA={斜三角形}.
答案:{斜三角形}
4.设全集U=R,集合X={x|x≥0},Y={y|y≥1},则
UY与 UX包含关系 UX__________ UY.
解析:∵X={x|x≥0},Y={y|y≥1},
∴ UX={x|x<0}, UY={y<1},∴ UX? UY.
互 动 课 堂
典 例 导 悟
类型一 补集的运算
[例1] 设U={x|2<|x|≤5,x∈Z},A={x|x2-2x-15=0},B={-3,3,4},求 UA, UB.
[解] 法1:∵2<|x|≤5,且x∈Z,
则x的值为-5,-4,-3,3,4,5;
方程x2-2x-15=0的解为5,-3,
∵A={5,-3},B={-3,3,4},
U={-5,-4,-3,3,4,5},
∴ UA={-5,-4,3,4}, UB={-5,-4,5}.
变式体验1 已知全集U,集合A={1,3,5,7,9}, UA={2,4,6,8}, UB={1,4,6,8,9},求集合B.
类型二 交、并、补的综合运算
[例2] 已知全集U={x|x≤4},集合A={x|-2[分析] 由题目可获取以下主要信息:①全集U,集合A、B均为无限集;②所求问题为集合间交、并、补运算.解答此题可借助数轴求解.
[解] 把全集U和集合A,B在数轴上表示如图3:
由图可知 UA={x|x≤-2或3≤x≤4},
A∩B={x|-2 U(A∩B)={x|x≤-2或3≤x≤4},
( UA)∩B={x|-3[点评] 求解用不等式表示的数集间的集合运算时,一般要借助于数轴求解,此法的特点是简单直观,同时要注意各个端点的画法及取到与否.
变式体验2 已知集合A={x|xA.a≤2 B.a<1
C.a≥2 D.a>2
答案:C
类型三 Venn图的应用
有些集合问题比较抽象,解题时若借助Venn图进行分析或利用数轴、图象采取数形结合的思想方法,往往可将问题直观化、形象化,使问题简捷地获解.
[例3] 已知集合U={x|x是不大于30的质数},A,B是U的两个子集,且满足A∩( UB)={5,13,23},B∩( UA)={11,19,29},( UA)∩( UB)={3,7},求集合A,B.
[分析] 结合Venn图可把全集U划分为如下四部分,全集U中的任一元素必在且只在图5四部分之一中,由题意可知11、13不在前三部分内,必然在A∩B内.
变式体验3 如图7(1)所示,设U为全集,M,P,N是U的三个子集,则图中阴影部分表示的集合是( )
A.(M∩P)∩N B.(M∩P)∪N
C.(M∩P)∩( UN) D.(M∩P)∪( UN)
解析:首先我们画出M∩P帮助我们思考,如图7(2),再结合图7(1),我们发现图中阴影部分为M∩P去掉被集合N覆盖的部分,换句话说即是与 UN做交运算.从而图7(1)中阴影部分表示的集合为(M∩P)∩( UN),故选C.
答案:C
点评:对于给定集合求阴影部分所表示的集合问题,可先确定两个主要的集合运算,对于去掉的部分可用与补集相交的方法来解决.
思 悟 升 华
1.全集是相对于研究问题而言的一个相对概念,它含有与所研究问题有关的各个集合的全部元素,因此,全集因研究问题而异.例如在研究数集时全集概念:在整数范围内研究问题,则Z为全集;而当问题扩展到实数集时,则R为全集,这时Z就不是全集.在立体几何中,三维空间是全集,这时平面是全集的一个子集.而在平面几何中,整个平面可以看做是一个全集.
2.补集符号: UA表示U为全集时A的补集,如果全集换成其他集合(如R)时,则记号中“U”也必须换成相应的集合(即 RA).
3.集合运算问题多与方程、函数、不等式等有关,在求解时,要注意等价转化思想的运用.常将集合化简或转化为熟知的代数、几何问题等.
4.处理集合的有关问题时,首先要将集合进行简化,在交、并、补的运算中,最容易被忽视、最常出错的地方是空集.
课时作业(5)
第一章
集合与函数概念
1.1 集合
1.1.3 集合的基本运算
第2课时
补集及集合的综合应用
1.理解在给定集合中一个子集的补集的含义与性质是本节的重点,一定要重点掌握.
2.并集、交集、补集的运算以及利用Venn图表达集合的关系与运算是考试的重点又是难点,在学习时要用心哦.
研 习 新 知
新 知 视 界
1.全集
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,我们就称这个集合为全集,记作U.
3.补集的性质
(1) U =U;
(2) UU= ;
(3) U( UA)=A;
(4)A∩( UA)= ,A∪( UA)=U;
(5)( UA)∪( UB)= U(A∩B).
自 我 检 测
1.设全集U={1,2,4,8},B={2,4},则 UB=( )
A.{1} B.{8}
C.{1,8} D.
答案:C
2.已知全集U={0,1,2},且 UA={2},则集合A的真子集共有( )
A.3个 B.4个
C.5个 D.6个
解析:∵U={0,1,2},且 UA={2},
∴A={0,1}.∴A的真子集是{0},{1}, 共3个,故选A.
答案:A
3.设集合S={三角形},A={直角三角形},则 SA=__________.
解析:三角形中去掉直角三角形,∴ SA={斜三角形}.
答案:{斜三角形}
4.设全集U=R,集合X={x|x≥0},Y={y|y≥1},则
UY与 UX包含关系 UX__________ UY.
解析:∵X={x|x≥0},Y={y|y≥1},
∴ UX={x|x<0}, UY={y<1},∴ UX? UY.
互 动 课 堂
典 例 导 悟
类型一 补集的运算
[例1] 设U={x|2<|x|≤5,x∈Z},A={x|x2-2x-15=0},B={-3,3,4},求 UA, UB.
[解] 法1:∵2<|x|≤5,且x∈Z,
则x的值为-5,-4,-3,3,4,5;
方程x2-2x-15=0的解为5,-3,
∵A={5,-3},B={-3,3,4},
U={-5,-4,-3,3,4,5},
∴ UA={-5,-4,3,4}, UB={-5,-4,5}.
变式体验1 已知全集U,集合A={1,3,5,7,9}, UA={2,4,6,8}, UB={1,4,6,8,9},求集合B.
类型二 交、并、补的综合运算
[例2] 已知全集U={x|x≤4},集合A={x|-2
[解] 把全集U和集合A,B在数轴上表示如图3:
由图可知 UA={x|x≤-2或3≤x≤4},
A∩B={x|-2
( UA)∩B={x|-3
变式体验2 已知集合A={x|x
C.a≥2 D.a>2
答案:C
类型三 Venn图的应用
有些集合问题比较抽象,解题时若借助Venn图进行分析或利用数轴、图象采取数形结合的思想方法,往往可将问题直观化、形象化,使问题简捷地获解.
[例3] 已知集合U={x|x是不大于30的质数},A,B是U的两个子集,且满足A∩( UB)={5,13,23},B∩( UA)={11,19,29},( UA)∩( UB)={3,7},求集合A,B.
[分析] 结合Venn图可把全集U划分为如下四部分,全集U中的任一元素必在且只在图5四部分之一中,由题意可知11、13不在前三部分内,必然在A∩B内.
变式体验3 如图7(1)所示,设U为全集,M,P,N是U的三个子集,则图中阴影部分表示的集合是( )
A.(M∩P)∩N B.(M∩P)∪N
C.(M∩P)∩( UN) D.(M∩P)∪( UN)
解析:首先我们画出M∩P帮助我们思考,如图7(2),再结合图7(1),我们发现图中阴影部分为M∩P去掉被集合N覆盖的部分,换句话说即是与 UN做交运算.从而图7(1)中阴影部分表示的集合为(M∩P)∩( UN),故选C.
答案:C
点评:对于给定集合求阴影部分所表示的集合问题,可先确定两个主要的集合运算,对于去掉的部分可用与补集相交的方法来解决.
思 悟 升 华
1.全集是相对于研究问题而言的一个相对概念,它含有与所研究问题有关的各个集合的全部元素,因此,全集因研究问题而异.例如在研究数集时全集概念:在整数范围内研究问题,则Z为全集;而当问题扩展到实数集时,则R为全集,这时Z就不是全集.在立体几何中,三维空间是全集,这时平面是全集的一个子集.而在平面几何中,整个平面可以看做是一个全集.
2.补集符号: UA表示U为全集时A的补集,如果全集换成其他集合(如R)时,则记号中“U”也必须换成相应的集合(即 RA).
3.集合运算问题多与方程、函数、不等式等有关,在求解时,要注意等价转化思想的运用.常将集合化简或转化为熟知的代数、几何问题等.
4.处理集合的有关问题时,首先要将集合进行简化,在交、并、补的运算中,最容易被忽视、最常出错的地方是空集.
课时作业(5)
