第13章全等三角形周清试卷2021-2022学年 华东师大版八年级上册数学(word版含答案)
文档属性
| 名称 | 第13章全等三角形周清试卷2021-2022学年 华东师大版八年级上册数学(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 537.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 10:17:40 | ||
图片预览

文档简介
新华师大版八年级上册数学
第13章 全等三角形周清试卷
姓名____________ 时间: 60分钟 满分:100分 总分____________
一、选择题(每小题3分,共15分)
1. 如图所示,在△ABC和△DEF中,,添加下列一个条件后,仍然不能证明△ABC≌△DEF的是 【 】
(A) (B) (C) (D)
2. 如图所示,在△ABC中,AC的垂直平分线交AB于点D,CD平分,若,则的度数为 【 】
(A) (B) (C) (D)
3. 如图所示,,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F,再分别以E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP,交CD于点M,若,则的度数为 【 】
(A) (B) (C) (D)
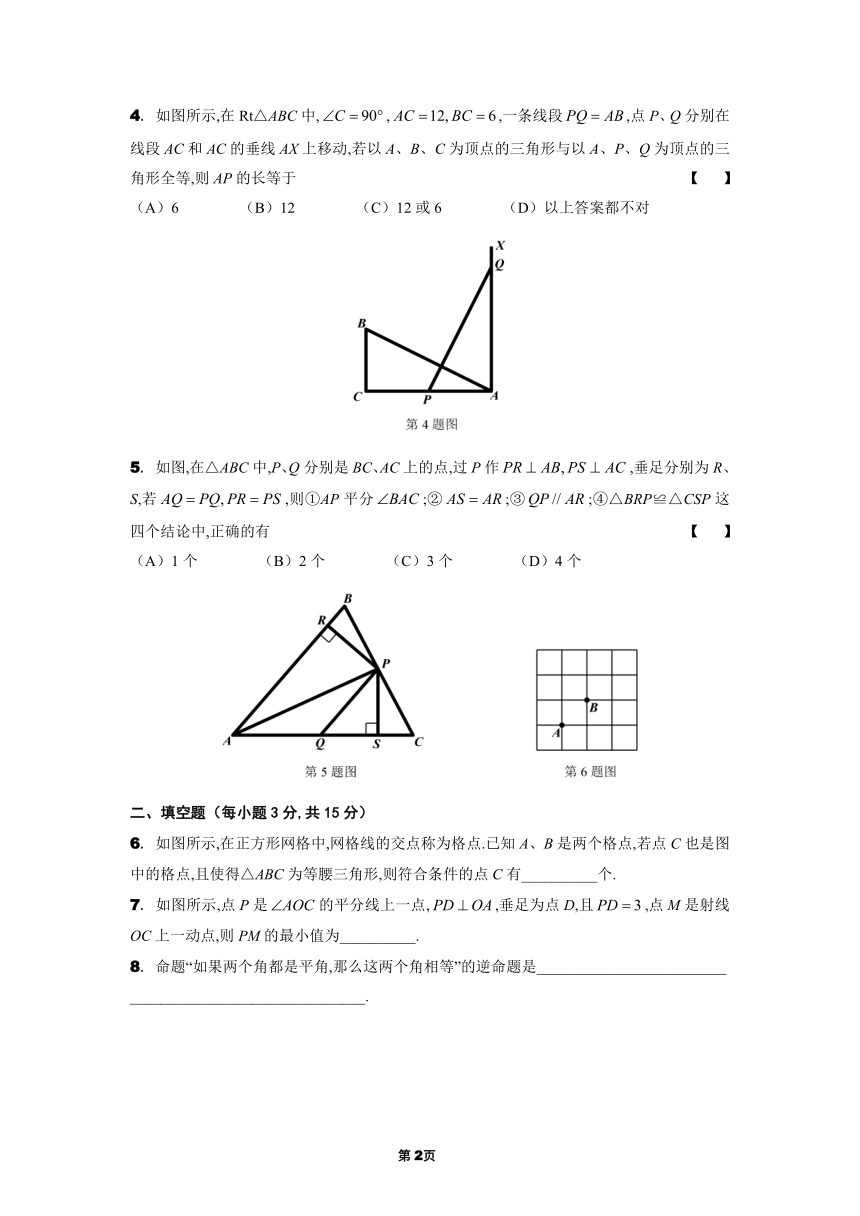
4. 如图所示,在Rt△ABC中,,,一条线段,点P、Q分别在线段AC和AC的垂线AX上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则AP的长等于 【 】
(A)6 (B)12 (C)12或6 (D)以上答案都不对
5. 如图,在△ABC中,P、Q分别是BC、AC上的点,过P作,垂足分别为R、S,若,则①AP平分;②;③;④△BRP≌△CSP这四个结论中,正确的有 【 】
(A)1个 (B)2个 (C)3个 (D)4个
二、填空题(每小题3分,共15分)
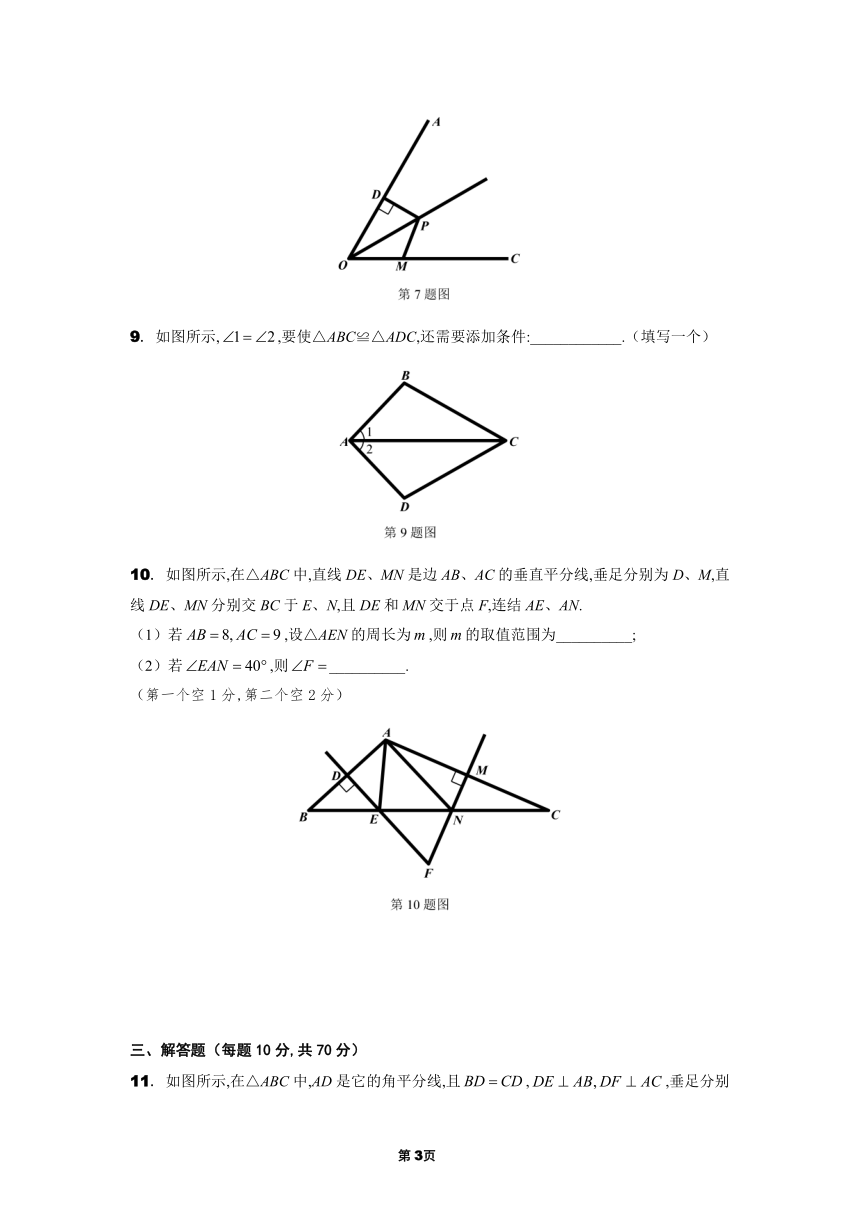
6. 如图所示,在正方形网格中,网格线的交点称为格点.已知A、B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有__________个.
7. 如图所示,点P是的平分线上一点,,垂足为点D,且,点M是射线OC上一动点,则PM的最小值为__________.
8. 命题“如果两个角都是平角,那么这两个角相等”的逆命题是_________________________
_______________________________.
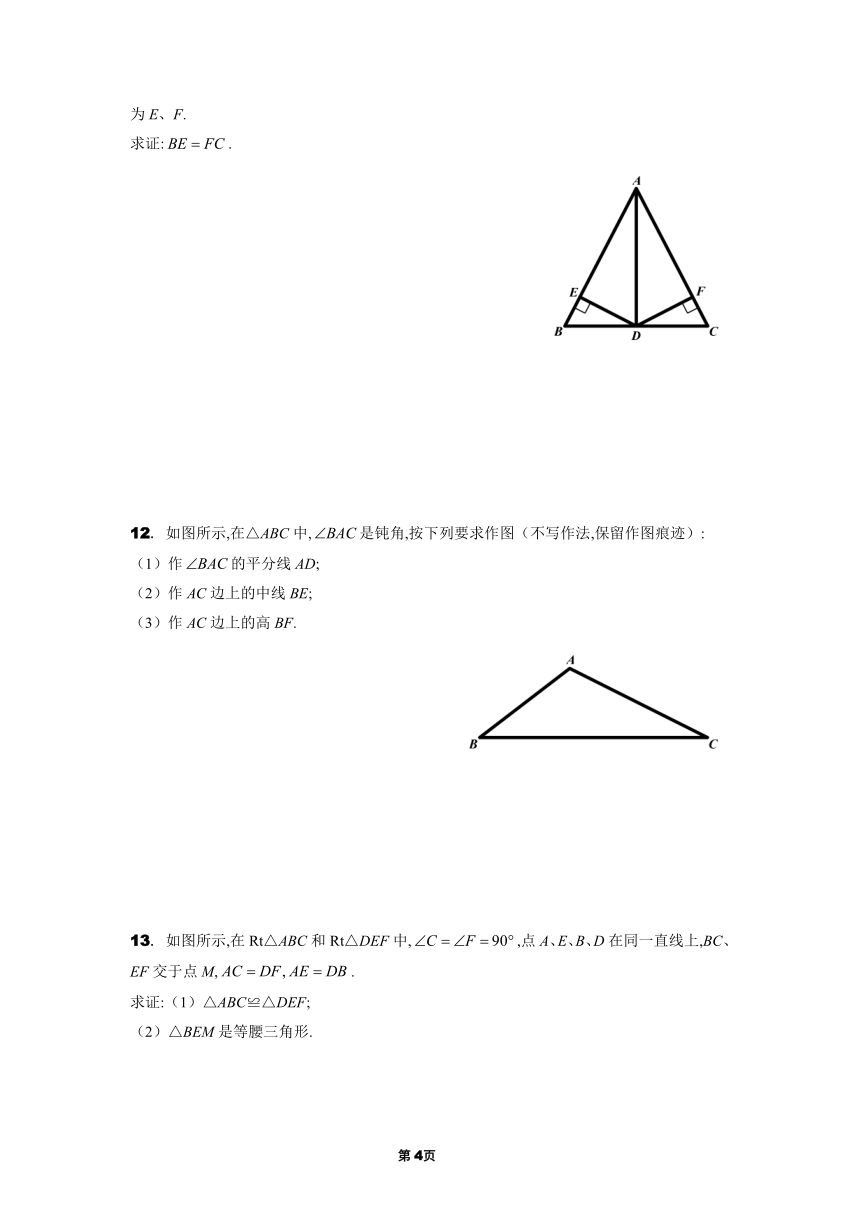
9. 如图所示,,要使△ABC≌△ADC,还需要添加条件:____________.(填写一个)
10. 如图所示,在△ABC中,直线DE、MN是边AB、AC的垂直平分线,垂足分别为D、M,直线DE、MN分别交BC于E、N,且DE和MN交于点F,连结AE、AN.
(1)若,设△AEN的周长为,则的取值范围为__________;
(2)若,则__________.
(第一个空1分,第二个空2分)
三、解答题(每题10分,共70分)
11. 如图所示,在△ABC中,AD是它的角平分线,且,,垂足分别为E、F.
求证:.
12. 如图所示,在△ABC中,是钝角,按下列要求作图(不写作法,保留作图痕迹):
(1)作的平分线AD;
(2)作AC边上的中线BE;
(3)作AC边上的高BF.
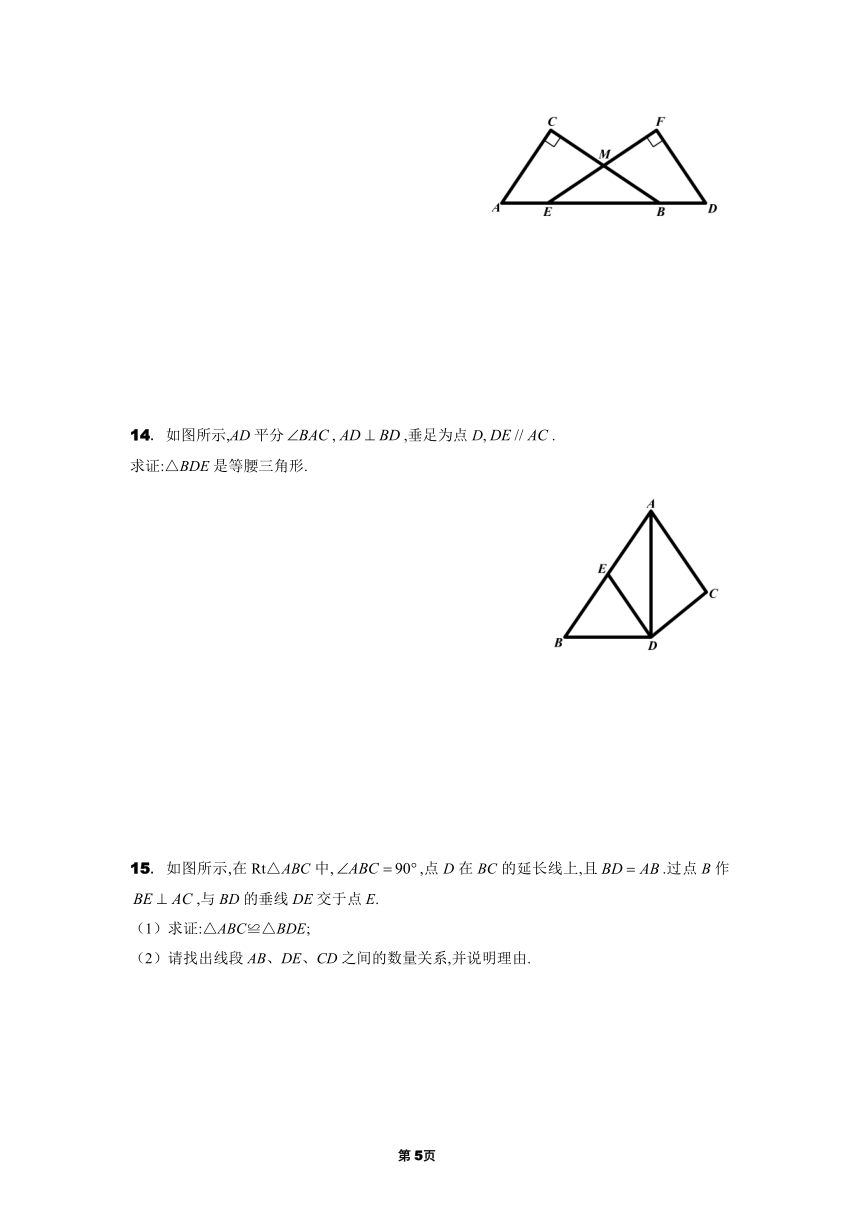
13. 如图所示,在Rt△ABC和Rt△DEF中,,点A、E、B、D在同一直线上,BC、EF交于点M,.
求证:(1)△ABC≌△DEF;
(2)△BEM是等腰三角形.
14. 如图所示,AD平分,,垂足为点D,.
求证:△BDE是等腰三角形.
15. 如图所示,在Rt△ABC中,,点D在BC的延长线上,且.过点B作,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
16. 如图所示,.
(1)添加条件__________,可利用SAS证明△ABE≌△CBF;
(2)在(1)的基础上,证明:△ABE≌△CBF.
17. 如图所示,已知△ABC为等边三角形,点D、E分别在BC、AC上,且,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求的度数.
新华师大版八年级上册数学
第13章 全等三角形周清试卷答案解析
一、选择题(每小题3分,共15分)
题号 1 2 3 4 5
答案 D B B C C
3. 如图所示,,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F,再分别以E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP,交CD于点M,若,则的度数为 【 】
(A) (B) (C) (D)
答案 【 B 】
解析 本题考查尺规作图的原理以及等腰三角形的判定(角平分线平行线模型).
由尺规作图可知:AM平分,∴.
∵,∴,.
∴
∴.
∴选择答案【 B 】.
4. 如图所示,在Rt△ABC中,,,一条线段,点P、Q分别在线段AC和AC的垂线AX上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则AP的长等于 【 】
(A)6 (B)12 (C)12或6 (D)以上答案都不对
答案 【 C 】
解析 本题考查三角形全等.
分为两种情况:
①当△APQ≌△CBA时,如图1所示.
此时,;
②当△APQ≌△CAB时,如图2所示.
此时,.
综上所述,AP的长等于12或6.
∴选择答案【 C 】.
5. 如图,在△ABC中,P、Q分别是BC、AC上的点,过P作,垂足分别为R、S,若,则①AP平分;②;③;④△BRP≌△CSP这四个结论中,正确的有 【 】
(A)1个 (B)2个
(C)3个 (D)4个
答案 【 C 】
解析 本题考查角平分线性质定理的逆定理、
平行线的判定定理以及三角形全等的知识.
对于结论①,∵,
∴点P在的平分线上
∴AP平分,故结论①正确;
对于结论②,易证:Rt△APS≌Rt△APR(HL).
∴.故结论②正确;
对于结论③,∵AP平分,∴.
∵,∴.
∴,∴.故结论③正确;
对于结论④,题目条件和图形不足以说明△BRP≌△CSP,故结论④错误.
综上所述,正确的结论有3个.
∴选择答案【 C 】.
二、填空题(每小题3分,共15分)
6. 8 7. 3 8. 如果两个角相等,那么这两个角是对顶角.
9. 或或 10.
6. 如图所示,在正方形网格中,网格线的交点称为格点.已知A、B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有__________个.
答案 8
解析 本题考查等腰三角形的存在性问题.
分别以点A、B为圆心,以AB的长为半径作圆,如图1所示,则可以找到这样的点C有4个.这两种情况下,△ABC是以AB为腰长的等腰三角形.
若AB为底边长,则作出AB的垂直平分线,如图2所示,可以找到这样的点C有4个.
综上所述,符合条件的点C有8个.
7. 如图所示,点P是的平分线上一点,,垂足为点D,且,点M是射线OC上一动点,则PM的最小值为__________.
答案 3
解析 本题考查角平分线的性质定理和垂线段最短.
根据垂线段最短可知,当时,PM取得最小值.
当时,结合,OP平分,可知.
∴PM的最小值为3.
8. 命题“如果两个角都是平角,那么这两个角相等”的逆命题是_________________________
_______________________________.
答案 如果两个角相等,那么这两个角是对顶角.
解析 本题考查互逆命题.
9. 如图所示,,要使△ABC≌△ADC,还需要添加条件:____________.(填写一个)
答案 或或
解析 本题考查全等三角形的判定定理.本题为开放性问题,应根据选择的判定定理并结合图形给出添加的条件,答案不唯一.
10. 如图所示,在△ABC中,直线DE、MN是边AB、AC的垂直平分线,垂足分别为D、M,直线DE、MN分别交BC于E、N,且DE和MN交于点F,连结AE、AN.
(1)若,设△AEN的周长为,则的取值范围为__________;
(2)若,则__________.(第一个空1分,第二个空2分)
答案
解析 本题主要考查垂直平分线的性质定理.
(1)∵DE、MN分别垂直平分AB、AC
∴
∴
∵
∴,即;
(2)在四边形ADFM中,易知.
∵,∴.
∵
∴
∴
∵
∴
∴
∴.
三、解答题(每题10分,共70分)
11. 如图所示,在△ABC中,AD是它的角平分线,且,,垂足分别为E、F.
求证:.
证明:∵AD平分,
∴,△BDE和△CDF都是直角三角形………………………………………………4分
在Rt△BDE和Rt△CDF中
∵
∴Rt△BDE≌Rt△CDF(HL)…………………………………………………………………8分
∴……………………………………………………………………………………10分
12. 如图所示,在△ABC中,是钝角,按下列要求作图(不写作法,保留作图痕迹):
(1)作的平分线AD;
(2)作AC边上的中线BE;
(3)作AC边上的高BF.
解:(1)如图所示; ……………………………………………………………………………3分
(2)如图所示;…………………………………………………………………………………6分
(3)如图所示; ………………………………………………………………………………10分
13. 如图所示,在Rt△ABC和Rt△DEF中,,点A、E、B、D在同一直线上,BC、EF交于点M,.
求证:(1)△ABC≌△DEF;
(2)△BEM是等腰三角形.
证明:(1)∵
∴
∴……………………………………………………………………………………1分
在Rt△ABC和Rt△DEF中
∵
∴Rt△ABC≌Rt△DEF(HL);………………………………………………………………6分
(2)由(1)知: Rt△ABC≌Rt△DEF
∴………………………………………………………………………………………7分
∴ …………………………………………………………………………………10分
∴△BEM是等腰三角形.
14. 如图所示,AD平分,,垂足为点D,.
求证:△BDE是等腰三角形.
证明:∵AD平分
∴………………………………………………………………………………………1分
∵
∴ ……………………………………………………………………………………2分
∴………………………………………………………………………………………3分
∵
∴…………………………………………………………5分
∴…………………………………………………………………………………6分
∴ ……………………………………………………………………………………9分
∴△BDE是等腰三角形.………………………………………………………………………10分
15. 如图所示,在Rt△ABC中,,点D在BC的延长线上,且.过点B作,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
(1)证明:∵,
∴………………………………………………………………………1分
∵
∴ …………………………………………………………………………2分
∵
∴………………………………………………………………………………………3分
在△ABC和△BDE中
∵
∴△ABC≌△BDE(ASA); …………………………………………………………………6分
(2)解:.………………………………………………………………………7分
理由如下:由(1)知:△ABC≌△BDE
∴ ……………………………………………………………………………………8分
∵
∴.……………………………………………………………………………10分
16. 如图所示,.
(1)添加条件__________,可利用SAS证明△ABE≌△CBF;
(2)在(1)的基础上,证明:△ABE≌△CBF.
(1)解:; ……………………………………………………………………………3分
(2)证明:∵
∴
∴ ……………………………………………………………………………4分
在△ABE和△CBF中
∵
∴△ABE≌△CBF(SAS). …………………………………………………………………10分
17. 如图所示,已知△ABC为等边三角形,点D、E分别在BC、AC上,且,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求的度数.
(1)证明:∵△ABC为等边三角形
∴……………………………………………………………1分
在△ABE和△CAD中
∵
∴△ABE≌△CAD(SAS); …………………………………………………………………6分
(2)解:由(1)知:△ABE≌△CAD
∴………………………………………………………………………………………7分
∵ ………………………………………………………………………9分
∴.……………………………………………………10分
PAGE
第17页
第13章 全等三角形周清试卷
姓名____________ 时间: 60分钟 满分:100分 总分____________
一、选择题(每小题3分,共15分)
1. 如图所示,在△ABC和△DEF中,,添加下列一个条件后,仍然不能证明△ABC≌△DEF的是 【 】
(A) (B) (C) (D)
2. 如图所示,在△ABC中,AC的垂直平分线交AB于点D,CD平分,若,则的度数为 【 】
(A) (B) (C) (D)
3. 如图所示,,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F,再分别以E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP,交CD于点M,若,则的度数为 【 】
(A) (B) (C) (D)
4. 如图所示,在Rt△ABC中,,,一条线段,点P、Q分别在线段AC和AC的垂线AX上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则AP的长等于 【 】
(A)6 (B)12 (C)12或6 (D)以上答案都不对
5. 如图,在△ABC中,P、Q分别是BC、AC上的点,过P作,垂足分别为R、S,若,则①AP平分;②;③;④△BRP≌△CSP这四个结论中,正确的有 【 】
(A)1个 (B)2个 (C)3个 (D)4个
二、填空题(每小题3分,共15分)
6. 如图所示,在正方形网格中,网格线的交点称为格点.已知A、B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有__________个.
7. 如图所示,点P是的平分线上一点,,垂足为点D,且,点M是射线OC上一动点,则PM的最小值为__________.
8. 命题“如果两个角都是平角,那么这两个角相等”的逆命题是_________________________
_______________________________.
9. 如图所示,,要使△ABC≌△ADC,还需要添加条件:____________.(填写一个)
10. 如图所示,在△ABC中,直线DE、MN是边AB、AC的垂直平分线,垂足分别为D、M,直线DE、MN分别交BC于E、N,且DE和MN交于点F,连结AE、AN.
(1)若,设△AEN的周长为,则的取值范围为__________;
(2)若,则__________.
(第一个空1分,第二个空2分)
三、解答题(每题10分,共70分)
11. 如图所示,在△ABC中,AD是它的角平分线,且,,垂足分别为E、F.
求证:.
12. 如图所示,在△ABC中,是钝角,按下列要求作图(不写作法,保留作图痕迹):
(1)作的平分线AD;
(2)作AC边上的中线BE;
(3)作AC边上的高BF.
13. 如图所示,在Rt△ABC和Rt△DEF中,,点A、E、B、D在同一直线上,BC、EF交于点M,.
求证:(1)△ABC≌△DEF;
(2)△BEM是等腰三角形.
14. 如图所示,AD平分,,垂足为点D,.
求证:△BDE是等腰三角形.
15. 如图所示,在Rt△ABC中,,点D在BC的延长线上,且.过点B作,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
16. 如图所示,.
(1)添加条件__________,可利用SAS证明△ABE≌△CBF;
(2)在(1)的基础上,证明:△ABE≌△CBF.
17. 如图所示,已知△ABC为等边三角形,点D、E分别在BC、AC上,且,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求的度数.
新华师大版八年级上册数学
第13章 全等三角形周清试卷答案解析
一、选择题(每小题3分,共15分)
题号 1 2 3 4 5
答案 D B B C C
3. 如图所示,,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F,再分别以E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP,交CD于点M,若,则的度数为 【 】
(A) (B) (C) (D)
答案 【 B 】
解析 本题考查尺规作图的原理以及等腰三角形的判定(角平分线平行线模型).
由尺规作图可知:AM平分,∴.
∵,∴,.
∴
∴.
∴选择答案【 B 】.
4. 如图所示,在Rt△ABC中,,,一条线段,点P、Q分别在线段AC和AC的垂线AX上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则AP的长等于 【 】
(A)6 (B)12 (C)12或6 (D)以上答案都不对
答案 【 C 】
解析 本题考查三角形全等.
分为两种情况:
①当△APQ≌△CBA时,如图1所示.
此时,;
②当△APQ≌△CAB时,如图2所示.
此时,.
综上所述,AP的长等于12或6.
∴选择答案【 C 】.
5. 如图,在△ABC中,P、Q分别是BC、AC上的点,过P作,垂足分别为R、S,若,则①AP平分;②;③;④△BRP≌△CSP这四个结论中,正确的有 【 】
(A)1个 (B)2个
(C)3个 (D)4个
答案 【 C 】
解析 本题考查角平分线性质定理的逆定理、
平行线的判定定理以及三角形全等的知识.
对于结论①,∵,
∴点P在的平分线上
∴AP平分,故结论①正确;
对于结论②,易证:Rt△APS≌Rt△APR(HL).
∴.故结论②正确;
对于结论③,∵AP平分,∴.
∵,∴.
∴,∴.故结论③正确;
对于结论④,题目条件和图形不足以说明△BRP≌△CSP,故结论④错误.
综上所述,正确的结论有3个.
∴选择答案【 C 】.
二、填空题(每小题3分,共15分)
6. 8 7. 3 8. 如果两个角相等,那么这两个角是对顶角.
9. 或或 10.
6. 如图所示,在正方形网格中,网格线的交点称为格点.已知A、B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有__________个.
答案 8
解析 本题考查等腰三角形的存在性问题.
分别以点A、B为圆心,以AB的长为半径作圆,如图1所示,则可以找到这样的点C有4个.这两种情况下,△ABC是以AB为腰长的等腰三角形.
若AB为底边长,则作出AB的垂直平分线,如图2所示,可以找到这样的点C有4个.
综上所述,符合条件的点C有8个.
7. 如图所示,点P是的平分线上一点,,垂足为点D,且,点M是射线OC上一动点,则PM的最小值为__________.
答案 3
解析 本题考查角平分线的性质定理和垂线段最短.
根据垂线段最短可知,当时,PM取得最小值.
当时,结合,OP平分,可知.
∴PM的最小值为3.
8. 命题“如果两个角都是平角,那么这两个角相等”的逆命题是_________________________
_______________________________.
答案 如果两个角相等,那么这两个角是对顶角.
解析 本题考查互逆命题.
9. 如图所示,,要使△ABC≌△ADC,还需要添加条件:____________.(填写一个)
答案 或或
解析 本题考查全等三角形的判定定理.本题为开放性问题,应根据选择的判定定理并结合图形给出添加的条件,答案不唯一.
10. 如图所示,在△ABC中,直线DE、MN是边AB、AC的垂直平分线,垂足分别为D、M,直线DE、MN分别交BC于E、N,且DE和MN交于点F,连结AE、AN.
(1)若,设△AEN的周长为,则的取值范围为__________;
(2)若,则__________.(第一个空1分,第二个空2分)
答案
解析 本题主要考查垂直平分线的性质定理.
(1)∵DE、MN分别垂直平分AB、AC
∴
∴
∵
∴,即;
(2)在四边形ADFM中,易知.
∵,∴.
∵
∴
∴
∵
∴
∴
∴.
三、解答题(每题10分,共70分)
11. 如图所示,在△ABC中,AD是它的角平分线,且,,垂足分别为E、F.
求证:.
证明:∵AD平分,
∴,△BDE和△CDF都是直角三角形………………………………………………4分
在Rt△BDE和Rt△CDF中
∵
∴Rt△BDE≌Rt△CDF(HL)…………………………………………………………………8分
∴……………………………………………………………………………………10分
12. 如图所示,在△ABC中,是钝角,按下列要求作图(不写作法,保留作图痕迹):
(1)作的平分线AD;
(2)作AC边上的中线BE;
(3)作AC边上的高BF.
解:(1)如图所示; ……………………………………………………………………………3分
(2)如图所示;…………………………………………………………………………………6分
(3)如图所示; ………………………………………………………………………………10分
13. 如图所示,在Rt△ABC和Rt△DEF中,,点A、E、B、D在同一直线上,BC、EF交于点M,.
求证:(1)△ABC≌△DEF;
(2)△BEM是等腰三角形.
证明:(1)∵
∴
∴……………………………………………………………………………………1分
在Rt△ABC和Rt△DEF中
∵
∴Rt△ABC≌Rt△DEF(HL);………………………………………………………………6分
(2)由(1)知: Rt△ABC≌Rt△DEF
∴………………………………………………………………………………………7分
∴ …………………………………………………………………………………10分
∴△BEM是等腰三角形.
14. 如图所示,AD平分,,垂足为点D,.
求证:△BDE是等腰三角形.
证明:∵AD平分
∴………………………………………………………………………………………1分
∵
∴ ……………………………………………………………………………………2分
∴………………………………………………………………………………………3分
∵
∴…………………………………………………………5分
∴…………………………………………………………………………………6分
∴ ……………………………………………………………………………………9分
∴△BDE是等腰三角形.………………………………………………………………………10分
15. 如图所示,在Rt△ABC中,,点D在BC的延长线上,且.过点B作,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
(1)证明:∵,
∴………………………………………………………………………1分
∵
∴ …………………………………………………………………………2分
∵
∴………………………………………………………………………………………3分
在△ABC和△BDE中
∵
∴△ABC≌△BDE(ASA); …………………………………………………………………6分
(2)解:.………………………………………………………………………7分
理由如下:由(1)知:△ABC≌△BDE
∴ ……………………………………………………………………………………8分
∵
∴.……………………………………………………………………………10分
16. 如图所示,.
(1)添加条件__________,可利用SAS证明△ABE≌△CBF;
(2)在(1)的基础上,证明:△ABE≌△CBF.
(1)解:; ……………………………………………………………………………3分
(2)证明:∵
∴
∴ ……………………………………………………………………………4分
在△ABE和△CBF中
∵
∴△ABE≌△CBF(SAS). …………………………………………………………………10分
17. 如图所示,已知△ABC为等边三角形,点D、E分别在BC、AC上,且,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求的度数.
(1)证明:∵△ABC为等边三角形
∴……………………………………………………………1分
在△ABE和△CAD中
∵
∴△ABE≌△CAD(SAS); …………………………………………………………………6分
(2)解:由(1)知:△ABE≌△CAD
∴………………………………………………………………………………………7分
∵ ………………………………………………………………………9分
∴.……………………………………………………10分
PAGE
第17页
