第四章图形的相似单元练习 2021—2022学年北师大版数学九年级上册(Word版含答案)
文档属性
| 名称 | 第四章图形的相似单元练习 2021—2022学年北师大版数学九年级上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 10:21:44 | ||
图片预览

文档简介
九年级上学期第四章图形的相似单元练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,AD是BC边上的高,∠C=45°,sinB=,AD=1.则△ABC的面积为( )
A.1 B. C. D.2
2.视力表用来测试一个人的视力,如图是视力表的一部分,图中的“E”均是相似图形,其中不是位似图形的是( )
A.①和④ B.②和③ C.①和② D.②和④
3.如图,在直角坐标系中,矩形的顶点在原点,边在轴上,在轴上,如果与关于点位似,且的面积等于面积的,则点的坐标为( )
A. B.或
C. D.或
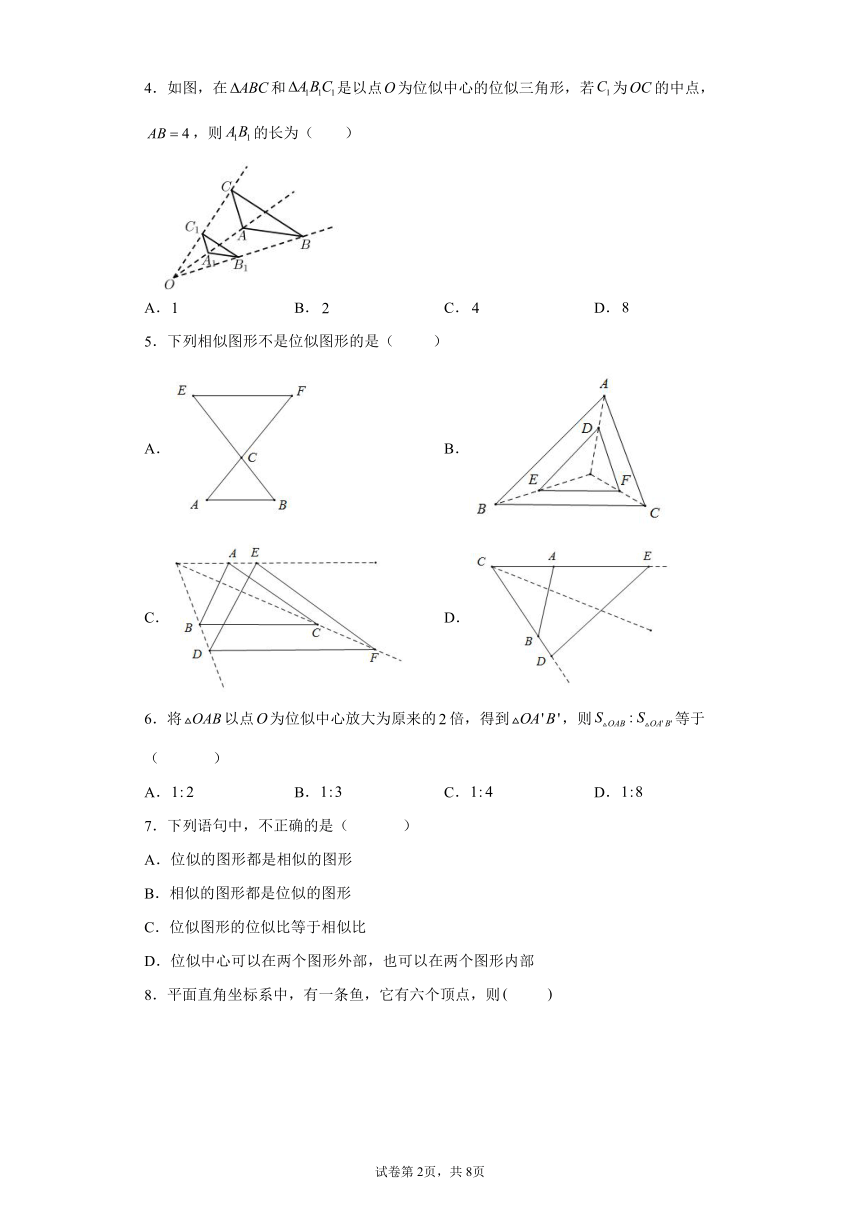
4.如图,在和是以点为位似中心的位似三角形,若为的中点,,则的长为( )
A. B. C. D.
5.下列相似图形不是位似图形的是( )
A. B.
C. D.
6.将以点为位似中心放大为原来的倍,得到,则等于( )
A. B. C. D.
7.下列语句中,不正确的是( )
A.位似的图形都是相似的图形
B.相似的图形都是位似的图形
C.位似图形的位似比等于相似比
D.位似中心可以在两个图形外部,也可以在两个图形内部
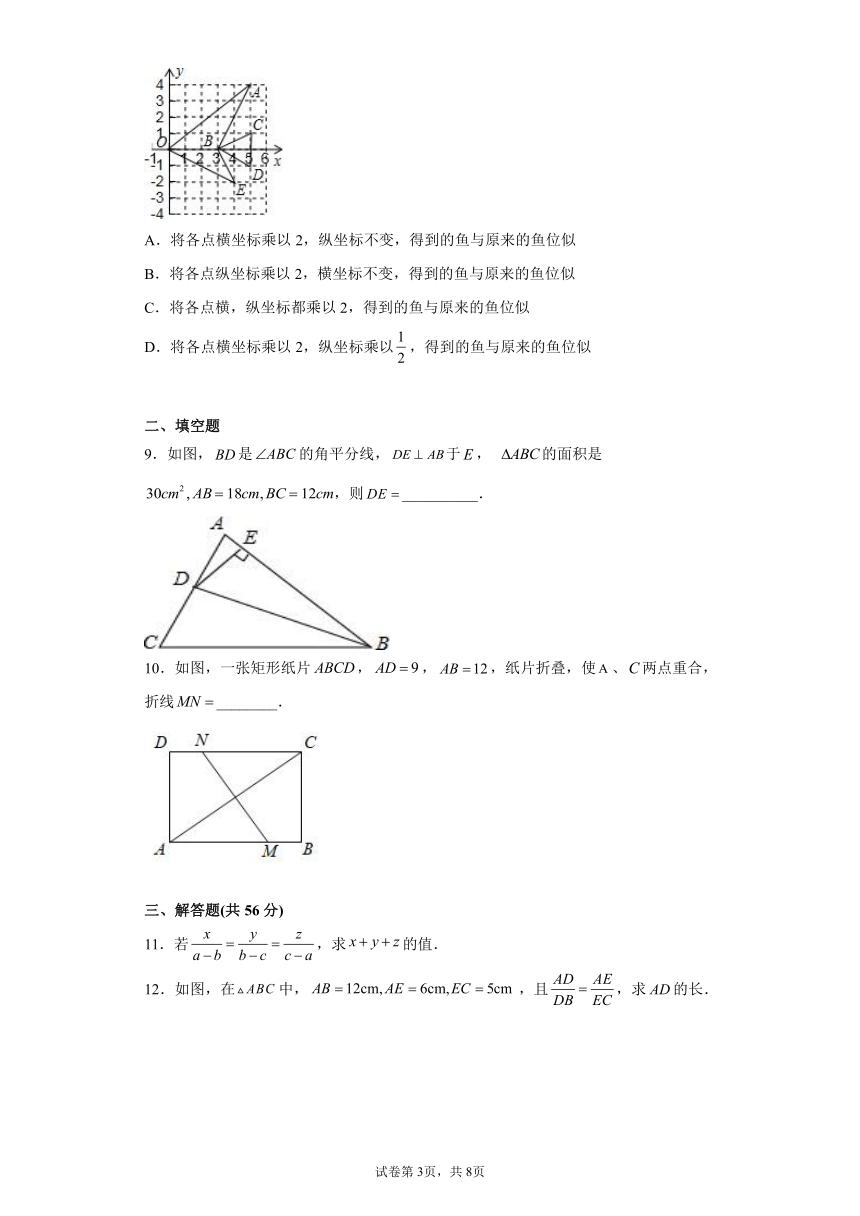
8.平面直角坐标系中,有一条鱼,它有六个顶点,则
A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似
B.将各点纵坐标乘以2,横坐标不变,得到的鱼与原来的鱼位似
C.将各点横,纵坐标都乘以2,得到的鱼与原来的鱼位似
D.将各点横坐标乘以2,纵坐标乘以,得到的鱼与原来的鱼位似
二、填空题
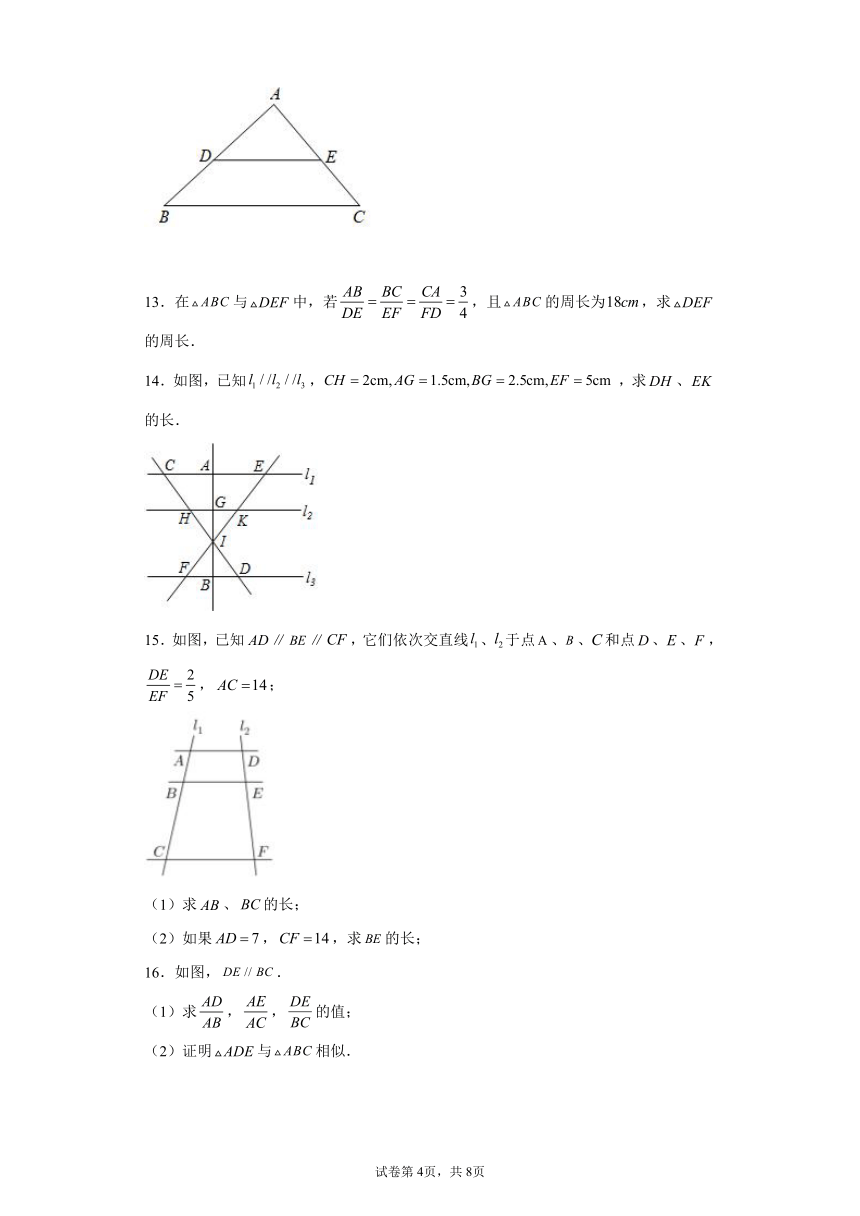
9.如图,是的角平分线,于, 的面积是,则__________.
10.如图,一张矩形纸片,,,纸片折叠,使、两点重合,折线________.
三、解答题(共56分)
11.若,求的值.
12.如图,在中,,且,求的长.
13.在与中,若,且的周长为,求的周长.
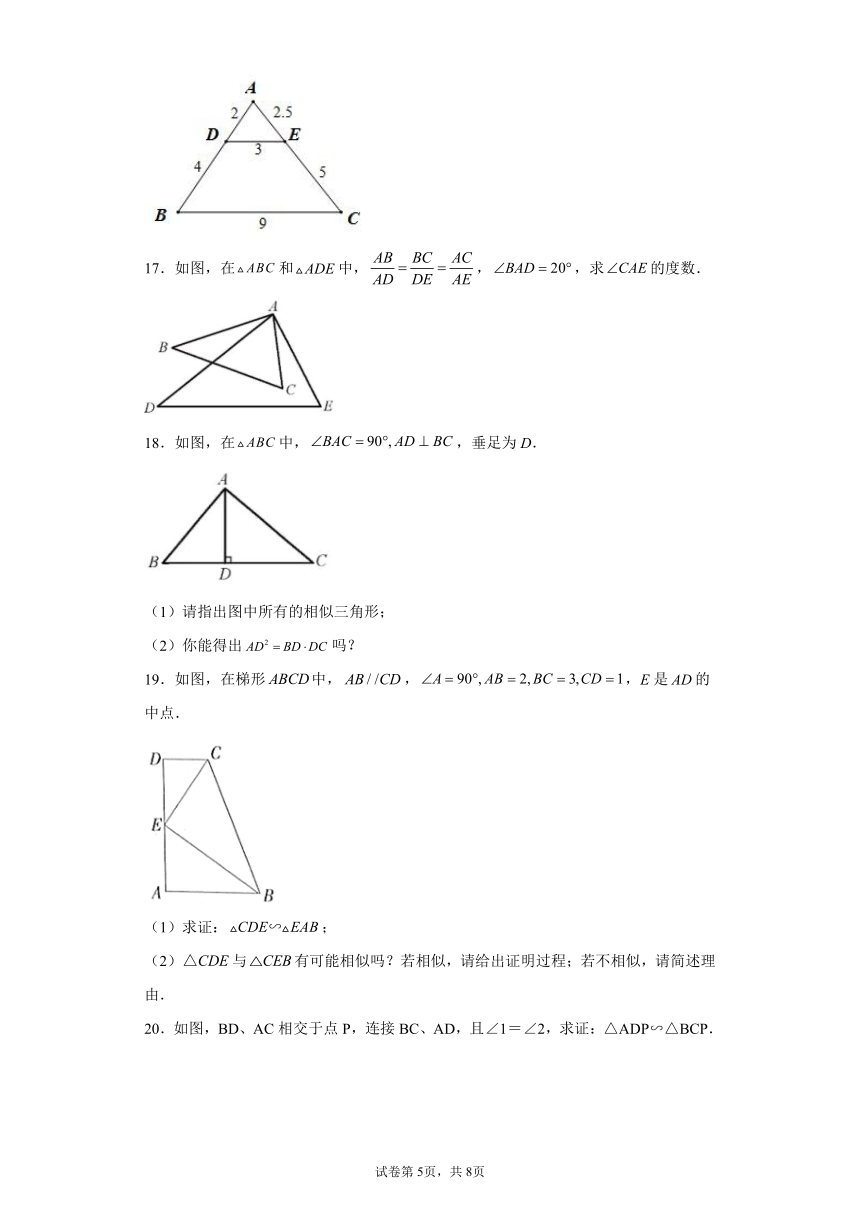
14.如图,已知,,求、的长.
15.如图,已知∥∥,它们依次交直线、于点、、和点、、,,;
(1)求、的长;
(2)如果,,求的长;
16.如图,.
(1)求,,的值;
(2)证明与相似.
17.如图,在和中,,,求的度数.
18.如图,在中,,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出吗?
19.如图,在梯形中,,,E是的中点.
(1)求证:;
(2)与有可能相似吗?若相似,请给出证明过程;若不相似,请简述理由.
20.如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,求证:△ADP∽△BCP.
21.旗杆的影子长,同时测得旗杆顶端到其影子顶端的距离是,如果此时附近小树的影子长,那么小树有多高?
22.如图,雨后初晴,小明在运动场上玩,当他在E点时发现前面2米处有一处积水C,从积水中看到旗杆顶端的倒影,若旗杆底部B距积水处40米,此时眼睛距地面1.5米.求旗杆的高度.
23.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.
24.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高.
25.如图,与相似,求x,y的值.
26.如图,在中,对角线与相交于点O,E是延长线上的一点,连接交于点F.已知,求的长.
27.已知,和是它们的对应中线,,求的长.
28.如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m.
(1)图中△ABC与△ADE是否相似?为什么?
(2)求古塔的高度.
29.如图,的三条边与的三条边满足,,,且.的面积与的面积之间有什么关系?
30.如图,正方形,都是正方形的位似图形,点P是位似中心.
(l)哪个图形与正方形的相似比为3?
(2)正方形是正方形的位似图形吗?如果是,求相似比.
(3)正方形与正方形的相似比是多少?
31.如图,在平面直角坐标系中,以原点O为位似中心,画出五边形的位似图形,使它与的相似比为.比较两个图形对应点的坐标,你能发现什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【分析】
先由三角形的高的定义得出∠ADB=∠ADC=90°,解Rt△ADB,得出AB=3,根据勾股定理求出BD=2,解Rt△ADC,得出DC=1,然后根据三角形的面积公式计算即可;
【详解】
在Rt△ABD中,
∵sinB==,
又∵AD=1,
∴AB=3,
∵BD2=AB2﹣AD2,
∴BD.
在Rt△ADC中,
∵∠C=45°,
∴CD=AD=1.
∴BC=BD+DC=2+1,
∴S△ABC= BC AD=×(2+1)×1=,
故选:C.
【点睛】
本题考查了三角形的面积问题,掌握三角形的面积公式是解题的关键.
2.B
【分析】
两个图形不仅是相似图形,而且每组对应点的连线都经过同一个点,对应边互相平行(或共线),那么这样的两个图形就是位似图形,根据定义即可解答.
【详解】
A.两个图形相似,且对应点的连线都经过同一个点,对应边互相平行,故是位似图形,
B.两个图形相似,但是对应点的连线不在同一个点,故不是位似图形,
C.两个图形相似,且对应点的连线都经过同一个点,对应边互相平行,故是位似图形,
D.两个图形相似,且对应点的连线都经过同一个点,对应边互相平行,故是位似图形,
故选:B.
【点睛】
此题考查位似图形,确定位似图形时确定对应点和对应边是解题的关键,由对应点连线交于一点,对应边互相平行即可判定图形是位似图形.
3.D
【分析】
由与关于点O位似,且的面积等于面积的,利用相似三角形的面积比等于相似比的平方,即可求得与的位似比为1:2,又由点B的坐标为(6,4),即可求得答案.
【详解】
解:∵与关于点O位似,
∴∽,
∵的面积等于面积的,
∴位似比为1:2,
∵点B的坐标为(6,4),
∴点B′的坐标是:(3,2)或(-3,-2).
故选D.
【点睛】
此题考查了位似图形的性质.此题难度不大,注意位似图形是特殊的相似图形,注意掌握相似三角形的面积比等于相似比的平方定理的应用,注意数形结合思想的应用.
4.B
【分析】
先利用位似图形的性质得出,然后根据位似图形的性质解答即可.
【详解】
为的中点,
和是以点为位似中心的位似三角形,
,
即
.
故选B.
【点睛】
本题主要考查了位似变换,正确应用位似图形的性质是解答本题关键.
5.D
【分析】
根据位似变换的概念判断即可.
【详解】
解:D中两个图形,对应边不互相平行,不是位似图形,
A、B、C中的图形符合位似变换的定义,是位似图形,
故选:D.
【点睛】
本题考查的是位似变换,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.
6.C
【分析】
利用位似图形的性质得出位似比进而得出面积比.
【详解】
∵ 将以点为位似中心放大为原来的倍,得到,
∴ 与的位似比为,
则=.
故选:C
【点睛】
此题主要考查了位似变换,正确得出位似比和面积比是解题关键.
7.B
【分析】
利用位似图形的性质分别判断得出即可.
【详解】
A、位似的图形都是相似的图形,正确,不合题意;
B、相似的图形不一定是位似的图形,错误,符合题意;
C、位似图形的位似比等于相似比,正确,不合题意;
D、位似中心可以在两个图形外部,也可以在两个图形内部,正确,不合题意.
故选:B.
【点睛】
此题主要考查了位似图形的性质,正确掌握位似图形的相关性质是解题关键.
8.C
【详解】
解:平面直角坐标系中图形的各个顶点,如果横纵坐标同时乘以同一个非0的实数k,得到的图形与原图形关于原点成位似图形,位似比是|k|.若乘的不是同一个数,得到的图形一定不会与原图形关于原点对称.故选C.
9.2cm
【分析】
过点D作,垂足为点F,根据BD是∠ABC的角平分线,得DE=DF,根据等高的三角形的面积之比等于其底边长之比,得△BDC与△BDA的面积之比,再求出△BDA的面积,进而求出DE.
【详解】
如图,过点D作,垂足为点F
∵BD是∠ABC的角平分线,
∴DE=DF
∵的面积是
∴
即
∴DE=2cm
故答案为:2cm.
【点睛】
本题考查了三角形的问题,掌握角平分线的性质、等高的三角形的面积之比等于其底边长之比是解题的关键.
10.
【分析】
如下图,连接AC交MN于点O,连接CM,由已知易得AC=15,由折叠的性质易得AM=CM,AO=CO=,∠AOM=∠CON=90°,这样设AM=x,在Rt△BCM中建立关于x的方程即可求得CM=,进而在Rt△CMO中可求得OM=,再证△AMO∽△CNO即可得到ON=OM,由此即可得到MN=.
【详解】
解:如下图,连接AC交MN于点O,连接CM,
∵在矩形ABCD中,BC=AD=9cm,AB=12cm,
∴AC=,
∵将矩形沿MN折叠后,点C与点A重合,
∴AM=CM,AO=CO=,∠AOM=∠CON=90°,
设AM=x,则CM=x,BM=12-x,
∵在Rt△CBM中,∠B=90°,BC=9cm,
∴,解得:,即CM=AM=cm,
∴在Rt△CMO中,OM=cm,
∵在矩形ABCD中,CD∥AB,
∴∠MAO=∠NCO,∠CNO=∠AMO,
∴△AMO∽△CNO
∴.,
∴cm,
∴cm,
故答案为:.
【点睛】
本题主要考查了矩形与折叠,勾股定理,相似三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.
11.0
【分析】
设,则,,,然后计算即可得到答案.
【详解】
解:∵,
设,
∴,,,
∴
=
=;
【点睛】
本题考查了比例的性质,求代数式的值,解题的关键是熟练掌握比例的性质进行解题.
12..
【分析】
利用比例线段得到,然后根据比例性质求.
【详解】
解:,即,
,
.
【点睛】
本题考查了比例线段、比例的性质,解题的关键是掌握对于四条线段、、、,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,如(即,我们就说这四条线段是成比例线段,简称比例线段.
13.
【分析】
根据相似三角形的判定与性质即可得.
【详解】
,
,
的周长与的周长之比为,
的周长等于18cm,
的周长为cm,
故答案为:24cm.
【点睛】
本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.
14.,.
【分析】
由可得,可求,可得,设,可得,解方程即可.
【详解】
解:∵
∴,
∴,
∴,
∴,,
设,
∴,
解得.
∴.
【点睛】
本题考查平行线截线段成比例性质,利用比例构建方程,掌握平行线截线段成比例性质,利用比例构建方程是解题关键.
15.(1)AB=4;BC=10;(2)9.
【分析】
(1)由平行线分线段成比例定理和比例的性质得出,即可求出AB的长,得出BC的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,得出AD=HE=GF=7,由平行线分线段成比例定理得出比例式求出BH,即可得出结果.
【详解】
(1)∵AD∥BE∥CF
∴
∴
∵AC=14
∴AB=4
∴BC=
(2)
过点A作AG∥DF交BE于点H,交CF于点G
又∵AD∥BE∥CF,AD=7
∴AD=HE=GF=7
∵CF=14
∴CG=147=7
∵BE∥CF
∴
∴BH=2
∴BE=2+7=9
【点睛】
本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;熟练掌握平行线分线段成比例,通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键.
16.(1);(2)见解析
【分析】
(1)由图可知、的长度,分别代入,,计算即可得本题答案;
(2)由(1)知和对应边成比例,由可知,,;再根据相似三角形的判定定理,对应边成比例,对应角分别相等的两个三角形相似,即可判定与相似.
【详解】
(1)∵,
∴,,,
即.
(2)由(1)知,,
又∵
∴,,,
∴∽(对应边成比例,对应角分别相等的两个三角形相似).
【点睛】
本题主要考查了比例线段及相似三角形的判定定理的知识,熟练掌握相关知识是解题的关键.
17.
【分析】
由在和中,,可证得,然后由相似三角形的对应角相等.
【详解】
解:在和中,,
,
,
,
.
【点睛】
本题考查了相似三角形的判定与性质,解题的关键是证明.
18.(1),,;(2),见解析
【分析】
(1)根据相似三角形的判定定理写出所有的相似三角形;
(2)利用两角对应相等的两个三角形相似证明,根据相似三角形的性质证明结论.
【详解】
解:(1),,;
(2)能,
,
,
,
,
,
,
,
,
;
【点睛】
本题考查的是相似三角形的判定和性质,解题的关键是掌握相似三角形的判定定理和性质定理.
19.(1)见解析;(2)相似,理由见解析
【分析】
(1)过点C作CF⊥AB于F,先证明四边形ADCF是矩形,得到AF=CD=1,AD=CF,BF=AB-AF=1,然后利用勾股定理求出,即可得到,再证明即可;
(2)利用勾股定理求出,,然后证明即可.
【详解】
解:(1)过点C作CF⊥AB于F,
∴∠A=∠CFA=∠CFB=90°,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠D=90°,
∴四边形ADCF是矩形,
∴AF=CD=1,AD=CF,
∴BF=AB-AF=1,
∴,
∵E是AD的中点,
∴,
∴,
∴,
又∵∠D=∠A=90°,
∴△CDE∽△EAB;
(2)△CDE∽△CEB相似,理由如下:
∵,,
∴,,,
∴ ,
∴△CDE∽△CEB.
【点睛】
本题主要考查了矩形的性质与判定,相似三角形的判定,勾股定理,平行的性质,解题的关键在于能够熟练掌握相关知识进行求解.
20.见解析
【分析】
根据两角对应相等,两三角形相似的判定定理得解.
【详解】
证明:∵∠1=∠2,∠DPA=∠CPB,∴△ADP∽△BCP.
【点睛】
本题考查相似三角形的判定,熟练掌握三角形相似的各种判定方法是解题关键.
21.
【分析】
根据题意可知旗杆、地面和影子组成的三角形是相似三角形,先根据勾股定理求出影长为的树的高度,然后根据对应边成比例求出树高即可.
【详解】
解:
由题意得,,,
在中,;
△,
,
即,
解得:,
答:树高为.
【点睛】
本题考查了相似三角形在测量高度时的应用,解题的关键是找出题中的相似三角形,并建立适当的数学模型来解决问题.
22.旗杆的高度为30米
【分析】
根据题意,可得直角△ABE与直角△CDE,根据镜面反射的性质求出△ABE∽△CDE,再根据其相似比解答.
【详解】
∵,,
∴,
又∵,
∴,
∴,即,
∴米,
∴旗杆的高度为30米.
【点睛】
本题考查了相似三角形的应用,应用反射的基本性质,得出三角形相似,运用相似比即可解答.
23.2.3米
【分析】
先根据同一时刻物高与影长成正比求出QD的影长,再根据此影长列出比例式即可
【详解】
解:如图,过点N作ND⊥PQ于D,则DN=PM,
∴△ABC∽△QDN,
.
∵AB=2米,BC=1.6米,PM=1.2米,NM=0.8米,
=1.5(米),
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木杆PQ的长度为2.3米.
【点睛】
此题考查相似三角形的应用和平行投影,解题关键在于掌握运算法则
24.树高为 5.5 米
【解析】
【分析】
根据两角相等的两个三角形相似,可得 △DEF∽△DCB ,利用相似三角形的对边成比例,可得, 代入数据计算即得BC的长,由 AB=AC+BC ,即可求出树高.
【详解】
∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB
∴ ,
∵DE=0.4m,EF=0.2m,CD=8m,
∴,
∴CB=4(m),
∴AB=AC+BC=1.5+4=5.5(米)
答:树高为 5.5 米.
【点睛】
本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型.
25.,或x= ,y=.
【分析】
由△ABC与△DEF相似,∠B、∠E为钝角,可知当,即时,△ABC∽△DEF;当,即时,△ABC∽△FED,继而求得答案.
【详解】
解:∵△ABC与△DEF相似,∠B、∠E为钝角,
∴∠B=∠E,
∴当,即时,△ABC∽△DEF,
解得:x=6,y= ;
当,即时,△ABC∽△FED,
解得:x= ,y=,
∴x=6,y=或x= ,y=.
【点睛】
此题考查了相似三角形的性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.
26..
【分析】
首先过点O作OMAB,交BC于点M,易得,,然后由相似三角形的对应边成比例,即可得出答案.
【详解】
解:过点O作OMAB,交BC于点M,
四边形ABCD是平行四边形
,
.
【点睛】
本题考查了平行四边形的性质以及相似三角形的判定及性质,此题难度适中,注意掌握辅助线的作法及数形结合思想的应用.
27..
【分析】
相似三角形对应中线的比等于相似比,即对应边的比.因而BD:B′D′=3:2解得:BD=6cm.
【详解】
解:∵△ABC∽△A′B′C′,
∴AC:A′C′=BD:B′D′,
∵,B′D′=4cm,
∴BD=6cm.
【点睛】
本题考查对相似三角形性质的理解,熟记相似三角形对应中线的比等于相似比是解题关键.
28.(1)相似,见解析;(2)16m
【分析】
(1)根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似;
(2)利用相似三角形的性质求得相应线段的长即可.
【详解】
解:(1)△ABC∽△ADE.
∵BC⊥AE,DE⊥AE,
∴∠ACB=∠AED=90°.
∵∠A=∠A,
∴△ABC∽△ADE;
(2)由(1)得△ABC∽△ADE,
∴
∵AC=2m,AE=2+18=20m,BC=1.6m,
∴,
∴DE=16m,
即古塔的高度为16m.
【点睛】
本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
29.的面积为的面积的9倍
【分析】
由条件可知△A′B′C′和△ABC是位似图形,且位似比为1:3,利用位似图形的性质可知△A′B′C′∽△ABC,可求得结论.
【详解】
解:的面积为的面积的9倍.
证明:∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴
∴,
∴,
∴,且相似比为3,
∴与的面积比为9.
【点睛】
本题考查了相似三角形的判定和性质,掌握位似图形的定义和性质是解题的关键.
30.(1)正方形;(2)是,正方形与正方形的相似比为;(3)正方形与正方形的相似比为2
【分析】
(1)利用位似比等于相似比求解;
(2)根据位似的定义和位似比等于相似比解决问题;
(3)利用位似比等于相似比求解.
【详解】
解:(1)因为PI:PA=6:2=3:1,
所以正方形IJKL与正方形ABCD的相似比为3;
(2)正方形IJKL是正方形EFGH的位似图形,
∴相似比为:;
(3)正方形EFGH与正方形ABCD的相似比为:.
【点睛】
本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行(或共线),那么这样的两个图形叫做位似图形,这个点叫做位似中心.两个图形必须是相似形;对应点的连线都经过同一点;
31.作图见解析;所得位似图形顶点的横坐标、纵坐标是五边形对应顶点横坐标、纵坐标的或.
【分析】
连接BO、CO、DO、EO,再分别取它们的中点B1、C1、D1、E1,顺次连接O、B1、C1、D1、E1即可,再分别延长BO、CO、DO、EO,再分别在其延长线上取点B1、C1、D1、E1,关于点O的对称点B2、C2、D2、E2,顺次连接O、B2、C2、D2、E2即可,再利用关于原点对称点的性质得出对应点坐标进而得出答案.
【详解】
解:如图所示:五边形和五边形即为所求,
由图可知:,,,;
,,,;
,,,;
比较两个图形的对应点的坐标可得:所得位似图形顶点的横坐标、纵坐标是五边形对应顶点横坐标、纵坐标的或.
【点睛】
本题考查了作图-位似变换:画位似图形的一般步骤,先确定位似中心,再分别连接并延长位似中心和能代表原图的关键点,接着根据位似比,确定能代表所作的位似图形的关键点,然后顺次连接上述各点,得到放大或缩小的图形.答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,AD是BC边上的高,∠C=45°,sinB=,AD=1.则△ABC的面积为( )
A.1 B. C. D.2
2.视力表用来测试一个人的视力,如图是视力表的一部分,图中的“E”均是相似图形,其中不是位似图形的是( )
A.①和④ B.②和③ C.①和② D.②和④
3.如图,在直角坐标系中,矩形的顶点在原点,边在轴上,在轴上,如果与关于点位似,且的面积等于面积的,则点的坐标为( )
A. B.或
C. D.或
4.如图,在和是以点为位似中心的位似三角形,若为的中点,,则的长为( )
A. B. C. D.
5.下列相似图形不是位似图形的是( )
A. B.
C. D.
6.将以点为位似中心放大为原来的倍,得到,则等于( )
A. B. C. D.
7.下列语句中,不正确的是( )
A.位似的图形都是相似的图形
B.相似的图形都是位似的图形
C.位似图形的位似比等于相似比
D.位似中心可以在两个图形外部,也可以在两个图形内部
8.平面直角坐标系中,有一条鱼,它有六个顶点,则
A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似
B.将各点纵坐标乘以2,横坐标不变,得到的鱼与原来的鱼位似
C.将各点横,纵坐标都乘以2,得到的鱼与原来的鱼位似
D.将各点横坐标乘以2,纵坐标乘以,得到的鱼与原来的鱼位似
二、填空题
9.如图,是的角平分线,于, 的面积是,则__________.
10.如图,一张矩形纸片,,,纸片折叠,使、两点重合,折线________.
三、解答题(共56分)
11.若,求的值.
12.如图,在中,,且,求的长.
13.在与中,若,且的周长为,求的周长.
14.如图,已知,,求、的长.
15.如图,已知∥∥,它们依次交直线、于点、、和点、、,,;
(1)求、的长;
(2)如果,,求的长;
16.如图,.
(1)求,,的值;
(2)证明与相似.
17.如图,在和中,,,求的度数.
18.如图,在中,,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出吗?
19.如图,在梯形中,,,E是的中点.
(1)求证:;
(2)与有可能相似吗?若相似,请给出证明过程;若不相似,请简述理由.
20.如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,求证:△ADP∽△BCP.
21.旗杆的影子长,同时测得旗杆顶端到其影子顶端的距离是,如果此时附近小树的影子长,那么小树有多高?
22.如图,雨后初晴,小明在运动场上玩,当他在E点时发现前面2米处有一处积水C,从积水中看到旗杆顶端的倒影,若旗杆底部B距积水处40米,此时眼睛距地面1.5米.求旗杆的高度.
23.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.
24.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高.
25.如图,与相似,求x,y的值.
26.如图,在中,对角线与相交于点O,E是延长线上的一点,连接交于点F.已知,求的长.
27.已知,和是它们的对应中线,,求的长.
28.如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m.
(1)图中△ABC与△ADE是否相似?为什么?
(2)求古塔的高度.
29.如图,的三条边与的三条边满足,,,且.的面积与的面积之间有什么关系?
30.如图,正方形,都是正方形的位似图形,点P是位似中心.
(l)哪个图形与正方形的相似比为3?
(2)正方形是正方形的位似图形吗?如果是,求相似比.
(3)正方形与正方形的相似比是多少?
31.如图,在平面直角坐标系中,以原点O为位似中心,画出五边形的位似图形,使它与的相似比为.比较两个图形对应点的坐标,你能发现什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【分析】
先由三角形的高的定义得出∠ADB=∠ADC=90°,解Rt△ADB,得出AB=3,根据勾股定理求出BD=2,解Rt△ADC,得出DC=1,然后根据三角形的面积公式计算即可;
【详解】
在Rt△ABD中,
∵sinB==,
又∵AD=1,
∴AB=3,
∵BD2=AB2﹣AD2,
∴BD.
在Rt△ADC中,
∵∠C=45°,
∴CD=AD=1.
∴BC=BD+DC=2+1,
∴S△ABC= BC AD=×(2+1)×1=,
故选:C.
【点睛】
本题考查了三角形的面积问题,掌握三角形的面积公式是解题的关键.
2.B
【分析】
两个图形不仅是相似图形,而且每组对应点的连线都经过同一个点,对应边互相平行(或共线),那么这样的两个图形就是位似图形,根据定义即可解答.
【详解】
A.两个图形相似,且对应点的连线都经过同一个点,对应边互相平行,故是位似图形,
B.两个图形相似,但是对应点的连线不在同一个点,故不是位似图形,
C.两个图形相似,且对应点的连线都经过同一个点,对应边互相平行,故是位似图形,
D.两个图形相似,且对应点的连线都经过同一个点,对应边互相平行,故是位似图形,
故选:B.
【点睛】
此题考查位似图形,确定位似图形时确定对应点和对应边是解题的关键,由对应点连线交于一点,对应边互相平行即可判定图形是位似图形.
3.D
【分析】
由与关于点O位似,且的面积等于面积的,利用相似三角形的面积比等于相似比的平方,即可求得与的位似比为1:2,又由点B的坐标为(6,4),即可求得答案.
【详解】
解:∵与关于点O位似,
∴∽,
∵的面积等于面积的,
∴位似比为1:2,
∵点B的坐标为(6,4),
∴点B′的坐标是:(3,2)或(-3,-2).
故选D.
【点睛】
此题考查了位似图形的性质.此题难度不大,注意位似图形是特殊的相似图形,注意掌握相似三角形的面积比等于相似比的平方定理的应用,注意数形结合思想的应用.
4.B
【分析】
先利用位似图形的性质得出,然后根据位似图形的性质解答即可.
【详解】
为的中点,
和是以点为位似中心的位似三角形,
,
即
.
故选B.
【点睛】
本题主要考查了位似变换,正确应用位似图形的性质是解答本题关键.
5.D
【分析】
根据位似变换的概念判断即可.
【详解】
解:D中两个图形,对应边不互相平行,不是位似图形,
A、B、C中的图形符合位似变换的定义,是位似图形,
故选:D.
【点睛】
本题考查的是位似变换,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.
6.C
【分析】
利用位似图形的性质得出位似比进而得出面积比.
【详解】
∵ 将以点为位似中心放大为原来的倍,得到,
∴ 与的位似比为,
则=.
故选:C
【点睛】
此题主要考查了位似变换,正确得出位似比和面积比是解题关键.
7.B
【分析】
利用位似图形的性质分别判断得出即可.
【详解】
A、位似的图形都是相似的图形,正确,不合题意;
B、相似的图形不一定是位似的图形,错误,符合题意;
C、位似图形的位似比等于相似比,正确,不合题意;
D、位似中心可以在两个图形外部,也可以在两个图形内部,正确,不合题意.
故选:B.
【点睛】
此题主要考查了位似图形的性质,正确掌握位似图形的相关性质是解题关键.
8.C
【详解】
解:平面直角坐标系中图形的各个顶点,如果横纵坐标同时乘以同一个非0的实数k,得到的图形与原图形关于原点成位似图形,位似比是|k|.若乘的不是同一个数,得到的图形一定不会与原图形关于原点对称.故选C.
9.2cm
【分析】
过点D作,垂足为点F,根据BD是∠ABC的角平分线,得DE=DF,根据等高的三角形的面积之比等于其底边长之比,得△BDC与△BDA的面积之比,再求出△BDA的面积,进而求出DE.
【详解】
如图,过点D作,垂足为点F
∵BD是∠ABC的角平分线,
∴DE=DF
∵的面积是
∴
即
∴DE=2cm
故答案为:2cm.
【点睛】
本题考查了三角形的问题,掌握角平分线的性质、等高的三角形的面积之比等于其底边长之比是解题的关键.
10.
【分析】
如下图,连接AC交MN于点O,连接CM,由已知易得AC=15,由折叠的性质易得AM=CM,AO=CO=,∠AOM=∠CON=90°,这样设AM=x,在Rt△BCM中建立关于x的方程即可求得CM=,进而在Rt△CMO中可求得OM=,再证△AMO∽△CNO即可得到ON=OM,由此即可得到MN=.
【详解】
解:如下图,连接AC交MN于点O,连接CM,
∵在矩形ABCD中,BC=AD=9cm,AB=12cm,
∴AC=,
∵将矩形沿MN折叠后,点C与点A重合,
∴AM=CM,AO=CO=,∠AOM=∠CON=90°,
设AM=x,则CM=x,BM=12-x,
∵在Rt△CBM中,∠B=90°,BC=9cm,
∴,解得:,即CM=AM=cm,
∴在Rt△CMO中,OM=cm,
∵在矩形ABCD中,CD∥AB,
∴∠MAO=∠NCO,∠CNO=∠AMO,
∴△AMO∽△CNO
∴.,
∴cm,
∴cm,
故答案为:.
【点睛】
本题主要考查了矩形与折叠,勾股定理,相似三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.
11.0
【分析】
设,则,,,然后计算即可得到答案.
【详解】
解:∵,
设,
∴,,,
∴
=
=;
【点睛】
本题考查了比例的性质,求代数式的值,解题的关键是熟练掌握比例的性质进行解题.
12..
【分析】
利用比例线段得到,然后根据比例性质求.
【详解】
解:,即,
,
.
【点睛】
本题考查了比例线段、比例的性质,解题的关键是掌握对于四条线段、、、,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,如(即,我们就说这四条线段是成比例线段,简称比例线段.
13.
【分析】
根据相似三角形的判定与性质即可得.
【详解】
,
,
的周长与的周长之比为,
的周长等于18cm,
的周长为cm,
故答案为:24cm.
【点睛】
本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.
14.,.
【分析】
由可得,可求,可得,设,可得,解方程即可.
【详解】
解:∵
∴,
∴,
∴,
∴,,
设,
∴,
解得.
∴.
【点睛】
本题考查平行线截线段成比例性质,利用比例构建方程,掌握平行线截线段成比例性质,利用比例构建方程是解题关键.
15.(1)AB=4;BC=10;(2)9.
【分析】
(1)由平行线分线段成比例定理和比例的性质得出,即可求出AB的长,得出BC的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,得出AD=HE=GF=7,由平行线分线段成比例定理得出比例式求出BH,即可得出结果.
【详解】
(1)∵AD∥BE∥CF
∴
∴
∵AC=14
∴AB=4
∴BC=
(2)
过点A作AG∥DF交BE于点H,交CF于点G
又∵AD∥BE∥CF,AD=7
∴AD=HE=GF=7
∵CF=14
∴CG=147=7
∵BE∥CF
∴
∴BH=2
∴BE=2+7=9
【点睛】
本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;熟练掌握平行线分线段成比例,通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键.
16.(1);(2)见解析
【分析】
(1)由图可知、的长度,分别代入,,计算即可得本题答案;
(2)由(1)知和对应边成比例,由可知,,;再根据相似三角形的判定定理,对应边成比例,对应角分别相等的两个三角形相似,即可判定与相似.
【详解】
(1)∵,
∴,,,
即.
(2)由(1)知,,
又∵
∴,,,
∴∽(对应边成比例,对应角分别相等的两个三角形相似).
【点睛】
本题主要考查了比例线段及相似三角形的判定定理的知识,熟练掌握相关知识是解题的关键.
17.
【分析】
由在和中,,可证得,然后由相似三角形的对应角相等.
【详解】
解:在和中,,
,
,
,
.
【点睛】
本题考查了相似三角形的判定与性质,解题的关键是证明.
18.(1),,;(2),见解析
【分析】
(1)根据相似三角形的判定定理写出所有的相似三角形;
(2)利用两角对应相等的两个三角形相似证明,根据相似三角形的性质证明结论.
【详解】
解:(1),,;
(2)能,
,
,
,
,
,
,
,
,
;
【点睛】
本题考查的是相似三角形的判定和性质,解题的关键是掌握相似三角形的判定定理和性质定理.
19.(1)见解析;(2)相似,理由见解析
【分析】
(1)过点C作CF⊥AB于F,先证明四边形ADCF是矩形,得到AF=CD=1,AD=CF,BF=AB-AF=1,然后利用勾股定理求出,即可得到,再证明即可;
(2)利用勾股定理求出,,然后证明即可.
【详解】
解:(1)过点C作CF⊥AB于F,
∴∠A=∠CFA=∠CFB=90°,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠D=90°,
∴四边形ADCF是矩形,
∴AF=CD=1,AD=CF,
∴BF=AB-AF=1,
∴,
∵E是AD的中点,
∴,
∴,
∴,
又∵∠D=∠A=90°,
∴△CDE∽△EAB;
(2)△CDE∽△CEB相似,理由如下:
∵,,
∴,,,
∴ ,
∴△CDE∽△CEB.
【点睛】
本题主要考查了矩形的性质与判定,相似三角形的判定,勾股定理,平行的性质,解题的关键在于能够熟练掌握相关知识进行求解.
20.见解析
【分析】
根据两角对应相等,两三角形相似的判定定理得解.
【详解】
证明:∵∠1=∠2,∠DPA=∠CPB,∴△ADP∽△BCP.
【点睛】
本题考查相似三角形的判定,熟练掌握三角形相似的各种判定方法是解题关键.
21.
【分析】
根据题意可知旗杆、地面和影子组成的三角形是相似三角形,先根据勾股定理求出影长为的树的高度,然后根据对应边成比例求出树高即可.
【详解】
解:
由题意得,,,
在中,;
△,
,
即,
解得:,
答:树高为.
【点睛】
本题考查了相似三角形在测量高度时的应用,解题的关键是找出题中的相似三角形,并建立适当的数学模型来解决问题.
22.旗杆的高度为30米
【分析】
根据题意,可得直角△ABE与直角△CDE,根据镜面反射的性质求出△ABE∽△CDE,再根据其相似比解答.
【详解】
∵,,
∴,
又∵,
∴,
∴,即,
∴米,
∴旗杆的高度为30米.
【点睛】
本题考查了相似三角形的应用,应用反射的基本性质,得出三角形相似,运用相似比即可解答.
23.2.3米
【分析】
先根据同一时刻物高与影长成正比求出QD的影长,再根据此影长列出比例式即可
【详解】
解:如图,过点N作ND⊥PQ于D,则DN=PM,
∴△ABC∽△QDN,
.
∵AB=2米,BC=1.6米,PM=1.2米,NM=0.8米,
=1.5(米),
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木杆PQ的长度为2.3米.
【点睛】
此题考查相似三角形的应用和平行投影,解题关键在于掌握运算法则
24.树高为 5.5 米
【解析】
【分析】
根据两角相等的两个三角形相似,可得 △DEF∽△DCB ,利用相似三角形的对边成比例,可得, 代入数据计算即得BC的长,由 AB=AC+BC ,即可求出树高.
【详解】
∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB
∴ ,
∵DE=0.4m,EF=0.2m,CD=8m,
∴,
∴CB=4(m),
∴AB=AC+BC=1.5+4=5.5(米)
答:树高为 5.5 米.
【点睛】
本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型.
25.,或x= ,y=.
【分析】
由△ABC与△DEF相似,∠B、∠E为钝角,可知当,即时,△ABC∽△DEF;当,即时,△ABC∽△FED,继而求得答案.
【详解】
解:∵△ABC与△DEF相似,∠B、∠E为钝角,
∴∠B=∠E,
∴当,即时,△ABC∽△DEF,
解得:x=6,y= ;
当,即时,△ABC∽△FED,
解得:x= ,y=,
∴x=6,y=或x= ,y=.
【点睛】
此题考查了相似三角形的性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.
26..
【分析】
首先过点O作OMAB,交BC于点M,易得,,然后由相似三角形的对应边成比例,即可得出答案.
【详解】
解:过点O作OMAB,交BC于点M,
四边形ABCD是平行四边形
,
.
【点睛】
本题考查了平行四边形的性质以及相似三角形的判定及性质,此题难度适中,注意掌握辅助线的作法及数形结合思想的应用.
27..
【分析】
相似三角形对应中线的比等于相似比,即对应边的比.因而BD:B′D′=3:2解得:BD=6cm.
【详解】
解:∵△ABC∽△A′B′C′,
∴AC:A′C′=BD:B′D′,
∵,B′D′=4cm,
∴BD=6cm.
【点睛】
本题考查对相似三角形性质的理解,熟记相似三角形对应中线的比等于相似比是解题关键.
28.(1)相似,见解析;(2)16m
【分析】
(1)根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似;
(2)利用相似三角形的性质求得相应线段的长即可.
【详解】
解:(1)△ABC∽△ADE.
∵BC⊥AE,DE⊥AE,
∴∠ACB=∠AED=90°.
∵∠A=∠A,
∴△ABC∽△ADE;
(2)由(1)得△ABC∽△ADE,
∴
∵AC=2m,AE=2+18=20m,BC=1.6m,
∴,
∴DE=16m,
即古塔的高度为16m.
【点睛】
本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
29.的面积为的面积的9倍
【分析】
由条件可知△A′B′C′和△ABC是位似图形,且位似比为1:3,利用位似图形的性质可知△A′B′C′∽△ABC,可求得结论.
【详解】
解:的面积为的面积的9倍.
证明:∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴
∴,
∴,
∴,且相似比为3,
∴与的面积比为9.
【点睛】
本题考查了相似三角形的判定和性质,掌握位似图形的定义和性质是解题的关键.
30.(1)正方形;(2)是,正方形与正方形的相似比为;(3)正方形与正方形的相似比为2
【分析】
(1)利用位似比等于相似比求解;
(2)根据位似的定义和位似比等于相似比解决问题;
(3)利用位似比等于相似比求解.
【详解】
解:(1)因为PI:PA=6:2=3:1,
所以正方形IJKL与正方形ABCD的相似比为3;
(2)正方形IJKL是正方形EFGH的位似图形,
∴相似比为:;
(3)正方形EFGH与正方形ABCD的相似比为:.
【点睛】
本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行(或共线),那么这样的两个图形叫做位似图形,这个点叫做位似中心.两个图形必须是相似形;对应点的连线都经过同一点;
31.作图见解析;所得位似图形顶点的横坐标、纵坐标是五边形对应顶点横坐标、纵坐标的或.
【分析】
连接BO、CO、DO、EO,再分别取它们的中点B1、C1、D1、E1,顺次连接O、B1、C1、D1、E1即可,再分别延长BO、CO、DO、EO,再分别在其延长线上取点B1、C1、D1、E1,关于点O的对称点B2、C2、D2、E2,顺次连接O、B2、C2、D2、E2即可,再利用关于原点对称点的性质得出对应点坐标进而得出答案.
【详解】
解:如图所示:五边形和五边形即为所求,
由图可知:,,,;
,,,;
,,,;
比较两个图形的对应点的坐标可得:所得位似图形顶点的横坐标、纵坐标是五边形对应顶点横坐标、纵坐标的或.
【点睛】
本题考查了作图-位似变换:画位似图形的一般步骤,先确定位似中心,再分别连接并延长位似中心和能代表原图的关键点,接着根据位似比,确定能代表所作的位似图形的关键点,然后顺次连接上述各点,得到放大或缩小的图形.答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
