2021-2022学年湖南省岳阳市岳阳县六校联考九年级(上)第一次月考数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南省岳阳市岳阳县六校联考九年级(上)第一次月考数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 385.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 00:00:00 | ||
图片预览



文档简介
2021-2022学年湖南省岳阳市岳阳县六校联考九年级(上)第一次月考数学试卷
一、单选题(本大道题共8小题,每题3分,满分24分)
1.(3分)下列方程是一元二次方程的是( )
A.2xy+1=0 B.x﹣=1 C.x2=2 D.ax2+bx+c=0
2.(3分)对于反比例函数y=,下列说法中不正确的是( )
A.y随x的增大而减小
B.它的图象在第一、三象限
C.点(﹣3,﹣1)在它的图象上
D.函数图象关于原点中心对称
3.(3分)一元二次方程4x2﹣4x+1=0的根的情况是( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
4.(3分)方程x2﹣6x﹣10=0变形时,下列变形正确的是( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
5.(3分)已知点A(﹣2,y1),B(﹣4,y2)都在反比例函数y=(k>0)的图象上,则y1,y2的大小关系( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法确定
6.(3分)如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b>的解集为( )
A.x<﹣6 B.﹣6<x<0或x>2
C.x>2 D.x<﹣6或0<x<2
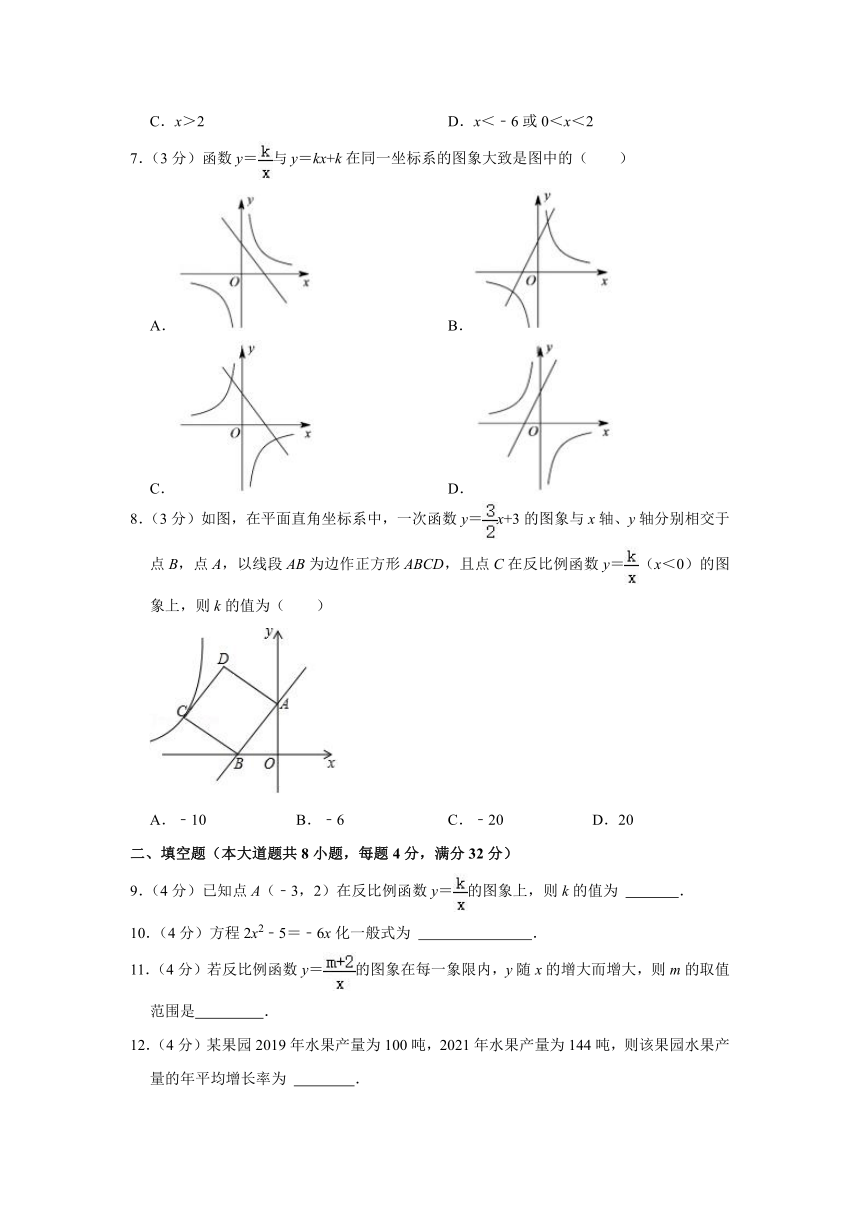
7.(3分)函数y=与y=kx+k在同一坐标系的图象大致是图中的( )
A. B.
C. D.
8.(3分)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴、y轴分别相交于点B,点A,以线段AB为边作正方形ABCD,且点C在反比例函数y=(x<0)的图象上,则k的值为( )
A.﹣10 B.﹣6 C.﹣20 D.20
二、填空题(本大道题共8小题,每题4分,满分32分)
9.(4分)已知点A(﹣3,2)在反比例函数y=的图象上,则k的值为 .
10.(4分)方程2x2﹣5=﹣6x化一般式为 .
11.(4分)若反比例函数y=的图象在每一象限内,y随x的增大而增大,则m的取值范围是 .
12.(4分)某果园2019年水果产量为100吨,2021年水果产量为144吨,则该果园水果产量的年平均增长率为 .
13.(4分)若方程3x2﹣5x﹣2=0有一根是a,则6a2﹣10a= .
14.(4分)如图,反比例函数y=(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作轴BE⊥x于点E,连接AD,已知AC=2,BE=2,S矩形BEOD=16,则S△ACD= .
15.(4分)中国民歌不仅脍炙人口,而且许多还有教育意义,有一首《牧童王小良》的民歌还包含着一个数学问题:
牧童王小良,放牧一群羊.问他羊几只,请你仔细想.头数加只数,只数减头数.只数乘头数,只数除头数.四数连加起,正好一百数.
如果设羊的只数为x,则根据民歌的大意,你能列出的方程是 .
16.(4分)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,
下列结论:
①BE+DF=EF;②CE=CF;③∠AEB=75°;④S正方形ABCD=2+,
其中正确的序号是 .
三、解答题(本大道题共8小题,满分64分)
17.(6分)当m为何值时,函数y=(m+3)x2﹣|m|是反比例函数?
18.(6分)先化简,再求值,其中x2+x﹣6=0.
19.(8分)解方程:
(1)8﹣2x2=0;
(2)x(2﹣x)=x﹣2.
20.(8分)如图,一次函数y=mx+n(m≠0)与反比例函数y=(k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积.
21.(8分)已知关于x的一元二次方程x2﹣mx﹣3=0.
(1)求证:无论m取何实数,该方程总有两个不相等的实数根;
(2)若方程的一根为3,求m的值及另一个根.
22.(8分)为抗击疫情,人们众志成城,响应号召,口罩成了生活必需品,某药店销售普通口罩和N95口罩.
(1)计划N95口罩每包售价比普通口罩贵16元,14包普通口罩和6包N95口罩总售价相同,求普通口罩和N95口罩每包售价;
(2)已知普通口罩每包进价8元,按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包.该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天普通口罩的利润为320元,求此时普通口罩每包售价.
23.(10分)如图所示,四边形ABCD为矩形,AB=6cm,AD=4cm,若点Q从A点出发沿AD以1cm/s的速度向D运动,P从B点出发沿BA以2cm/s的速度向A运动,如果P、Q分别同时出发,当一个点到达终点时,另一点也同时停止.设运动的时间为t(s).
(1)当t为何值时,△PAQ为等腰三角形?
(2)当t为何值时,△APD的面积为6cm2?
(3)五边形PBCDQ的面积能否达到20cm2?若能,请求出t的值;若不能,请说明理由.
(4)当t为何值时,P、Q两点之间的距离为cm?
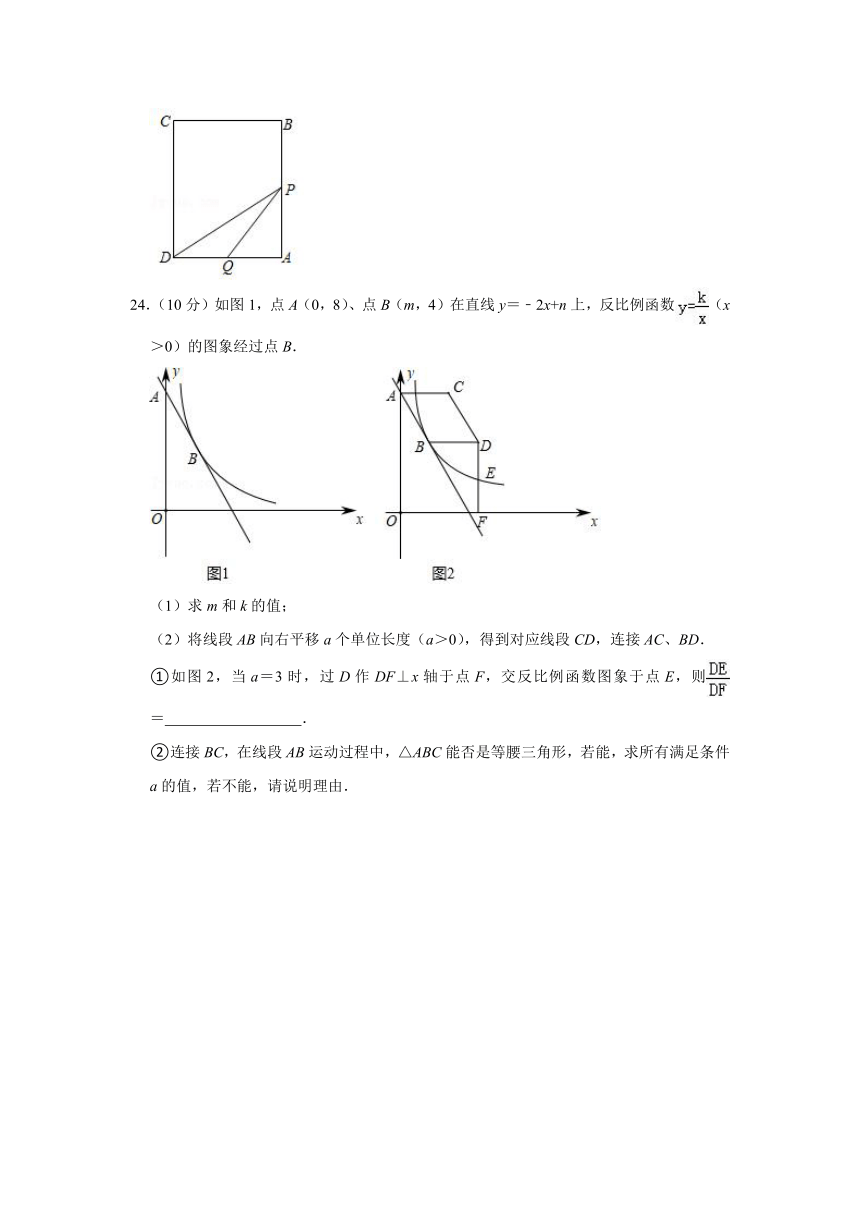
24.(10分)如图1,点A(0,8)、点B(m,4)在直线y=﹣2x+n上,反比例函数(x>0)的图象经过点B.
(1)求m和k的值;
(2)将线段AB向右平移a个单位长度(a>0),得到对应线段CD,连接AC、BD.
①如图2,当a=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,则= .
②连接BC,在线段AB运动过程中,△ABC能否是等腰三角形,若能,求所有满足条件a的值,若不能,请说明理由.
2021-2022学年湖南省岳阳市岳阳县六校联考九年级(上)第一次月考数学试卷
参考答案与试题解析
一、单选题(本大道题共8小题,每题3分,满分24分)
1.(3分)下列方程是一元二次方程的是( )
A.2xy+1=0 B.x﹣=1 C.x2=2 D.ax2+bx+c=0
【分析】利用一元二次方程定义进行解答即可.
【解答】解:A、含有2个未知数,不是一元二次方程,故此选项不符合题意;
B、是分式方程,故此选项不符合题意;
C、是一元二次方程,故此选项符合题意;
D、当a=0时,该方程不是一元二次方程,故此选项不符合题意.
故选:C.
2.(3分)对于反比例函数y=,下列说法中不正确的是( )
A.y随x的增大而减小
B.它的图象在第一、三象限
C.点(﹣3,﹣1)在它的图象上
D.函数图象关于原点中心对称
【分析】根据题目中的函数解析式和反比例函数的性质,可以判断各个选项中的说法是否正确,本题得以解决.
【解答】解:∵反比例函数y=,
∴该函数图象在第一、三象限,故选项B正确;
在每个象限内,y随x的增大而减小,故选项A错误;
当x=﹣3时,y=﹣1,即点(﹣3,﹣1)在它的图象上,故选项C正确;
函数图象关于原点中心对称,故选项D正确;
故选:A.
3.(3分)一元二次方程4x2﹣4x+1=0的根的情况是( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
【分析】根据方程的系数结合根的判别式,可得出Δ=0,进而可得出一元二次方程4x2﹣4x+1=0有两个相等的实数根.
【解答】解:∵Δ=(﹣4)2﹣4×4×1=0,
∴一元二次方程4x2﹣4x+1=0有两个相等的实数根.
故选:C.
4.(3分)方程x2﹣6x﹣10=0变形时,下列变形正确的是( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
【分析】根据配方法即可求出答案.
【解答】解:∵x2﹣6x﹣10=0,
∴x2﹣6x=10,
∴x2﹣6x+9=19,
∴(x﹣3)2=19,
故选:D.
5.(3分)已知点A(﹣2,y1),B(﹣4,y2)都在反比例函数y=(k>0)的图象上,则y1,y2的大小关系( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法确定
【分析】直接利用反比例函数的增减性分析得出答案.
【解答】解:∵反比例函数y=(k>0)中,k>0,
∴在每个象限内,y随x的增大而减小,
∵点A(﹣2,y1),B(﹣4,y2)都在反比例函数y=(k>0)的图象上,且﹣2>﹣4
∴y1<y2,
故选:B.
6.(3分)如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b>的解集为( )
A.x<﹣6 B.﹣6<x<0或x>2
C.x>2 D.x<﹣6或0<x<2
【分析】根据函数的图象和交点坐标即可求得结果.
【解答】解:不等式kx+b>的解集为:﹣6<x<0或x>2,
故选:B.
7.(3分)函数y=与y=kx+k在同一坐标系的图象大致是图中的( )
A. B.
C. D.
【分析】因为k的符号不确定,所以应根据k的符号及一次函数与反比例函数图象的性质解答.
【解答】解:∵y=kx+k=k(x+1),
∴直线经过点(﹣1,0),故A、C选项错误;
当k<0时,反比例函数y=的图象在二,四象限,一次函数y=kx+k的图象过二、三、四象限,选项B、D不符合;
当k>0时,反比例函数y=的图象在一、三象限,一次函数y=kx+k的图象过一、二、三象限,选项B符合.
故选:B.
8.(3分)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴、y轴分别相交于点B,点A,以线段AB为边作正方形ABCD,且点C在反比例函数y=(x<0)的图象上,则k的值为( )
A.﹣10 B.﹣6 C.﹣20 D.20
【分析】过点C作CE⊥x轴于E,证明△AOB≌△BEC,可得点C坐标,代入求解即可.
【解答】解:∵当x=0时,y=×0+3=3,
∴A(0,3),
∴OA=3;
∵当y=0时,0=x+3,
∴x=﹣2,
∴B(﹣2,0),
∴OB=2;
过点C作CE⊥x轴于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠CBE+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
在△AOB和△BEC中,
,
∴△AOB≌△BEC(AAS),
∴BE=AO=3,CE=OB=2,
∴OE=3+2=5,
∴C点坐标为(﹣5,2),
∵点C在反比例函数y=(x<0)的图象上,
∴k=﹣5×2=﹣10.
故选:A.
二、填空题(本大道题共8小题,每题4分,满分32分)
9.(4分)已知点A(﹣3,2)在反比例函数y=的图象上,则k的值为 ﹣6 .
【分析】根据点A的坐标,利用反比例函数图象上点的坐标特征求出k值,此题得解.
【解答】解:∵点A(﹣3,2)在反比例函数y=的图象上,
∴k=(﹣3)×2=﹣6.
故答案为:﹣6.
10.(4分)方程2x2﹣5=﹣6x化一般式为 2x2+6x﹣5=0 .
【分析】移项后即可得出一元二次方程的一般形式.
【解答】解:2x2﹣5=﹣6x,
移项,得2x2+6x﹣5=0,
故答案为:2x2+6x﹣5=0.
11.(4分)若反比例函数y=的图象在每一象限内,y随x的增大而增大,则m的取值范围是 m<﹣2 .
【分析】根据反比例函数的性质得到m+2<0,然后解一元一次不等式即可.
【解答】解:根据题意得m+2<0,
解得m<﹣2.
故答案为m<﹣2.
12.(4分)某果园2019年水果产量为100吨,2021年水果产量为144吨,则该果园水果产量的年平均增长率为 20% .
【分析】可根据二次增长公式a(1+x)2=b,列出以增长率为未知数的方程,求出增长率.
【解答】解:设该果园水果产量的年平均增长率为x,根据题意,得
100(1+x)2=144,
解方程得x1=0.2,x2=﹣2.2.x2=﹣2.2不符合题意,舍去.
故答案为20%.
13.(4分)若方程3x2﹣5x﹣2=0有一根是a,则6a2﹣10a= 4 .
【分析】将a代入方程3x2﹣5x﹣2=0,得到3a2﹣5a=2,等式的两边都扩大为原来的2倍,问题可求.
【解答】解:由题意,把是a的根代入3x2﹣5x﹣2=0,
得:3a2﹣5a=2,
∴2×(3a2﹣5a)=2×2,
∴6a2﹣10a=4.
14.(4分)如图,反比例函数y=(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作轴BE⊥x于点E,连接AD,已知AC=2,BE=2,S矩形BEOD=16,则S△ACD= 6 .
【分析】利用反比例函数比例系数k的几何意义得到S矩形BEOD=|k|=16,则求出k得到反比例函数的解析式为y=,再利用A点的横坐标为2可计算出A点的纵坐标为8,从而得到CD=6,然后根据三角形面积公式计算S△ACD.
【解答】解:∵BE⊥x轴于E,BD⊥y轴于D,
∴S矩形BEOD=|k|=16,
而k<0,
∴k=16,
∴反比例函数的解析式为y=,
∵AC⊥y轴,AC=2,
∴A点的横坐标为2,
当x=2时,y==8,
∴CD=OC﹣OD=8﹣2=6,
∴S△ACD=×2×6=6.
故答案为6.
15.(4分)中国民歌不仅脍炙人口,而且许多还有教育意义,有一首《牧童王小良》的民歌还包含着一个数学问题:
牧童王小良,放牧一群羊.问他羊几只,请你仔细想.头数加只数,只数减头数.只数乘头数,只数除头数.四数连加起,正好一百数.
如果设羊的只数为x,则根据民歌的大意,你能列出的方程是 x2+2x+1=100 .
【分析】等量关系为:头数加只数+只数减头数+只数乘头数+只数除头数=100,把相关数值代入化简即可.
【解答】解:∵羊的只数为x,
∴头数加只数为2x,只数减头数为0.只数乘头数为x2,只数除头数为1,
∴可列方程为:x2+2x+1=100,
故答案为:x2+2x+1=100.
16.(4分)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,
下列结论:
①BE+DF=EF;②CE=CF;③∠AEB=75°;④S正方形ABCD=2+,
其中正确的序号是 ②③④ .
【分析】由正方形的性质得AB=AD,∠B=∠D=90°,由等边三角形的性质得AE=AF,则可判断Rt△ABE≌△ADF,得到BE=DF,∠BAE=∠DAF,加上∠EAF=60°,易得∠BAE=∠DAF=15°,利用互余得∠AEB=75°,则可对③进行判断;由于CB=CD,BE=DF,则CE=CF,于是可对②进行判断;先判断△CEF为等腰直角三角形得到CE=CF=EF=,设正方形的边长为x,则AB=x,BE=x﹣,在Rt△ABE中利用勾股定理得x2+(x﹣)2=22,解得x1=,x2=(舍去),则可计算出BE+DF=﹣,于是可判断①错误;然后利用正方形面积公式可对④进行判断.
【解答】解:∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°,
∵△AEF为等边三角形,
∴AE=AF,
在Rt△ABE和△ADF中,
,
∴Rt△ABE≌△ADF,
∴BE=DF,∠BAE=∠DAF,
而∠EAF=60°,
∴∠BAE=∠DAF=15°,
∴∠AEB=75°,所以③正确,
∵CB=CD,
∴CB﹣BE=CD﹣DF,
即CE=CF,所以②正确;
∴△CEF为等腰直角三角形,
∴CE=CF=EF=,
设正方形的边长为x,则AB=x,BE=x﹣,
在Rt△ABE中,∵AB2+BE2=AE2,
∴x2+(x﹣)2=22,
整理得x2﹣x﹣1=0,解得x1=,x2=(舍去),
∴BE+DF=2(x﹣)=2(﹣)=﹣≠2,所以①错误;
∴S正方形ABCD=x2=()2=2+,所以④正确.
对于①的判断可用下面的方法:
连接AC交EF于G,如图,
∵AE=AF,CE=CF,
∴AC垂直平分EF,
∴EG=FG,
∵∠BAE=15°,∠GAE=30°,
∴BE=AE sin15°,EG=AE sin30°,
∴BE≠EG,
∴BE+DF≠EF,所以①错误.
故答案为②③④.
三、解答题(本大道题共8小题,满分64分)
17.(6分)当m为何值时,函数y=(m+3)x2﹣|m|是反比例函数?
【分析】根据反比例函数的定义得出2﹣|m|=﹣1且m+3≠0,再求出m即可.
【解答】解:∵函数y=(m+3)x2﹣|m|是反比例函数,
∴2﹣|m|=﹣1且m+3≠0,
解得:m=3,
即当m=3时,函数y=(m+3)x2﹣|m|是反比例函数.
18.(6分)先化简,再求值,其中x2+x﹣6=0.
【分析】先按照分式乘除法法则化简计算,再解一元二次方程求解x值,后代入计算可求解.
【解答】解:原式=
=x+1,
∵x2+x﹣6=0,
∴x1=﹣3,x2=2,
∵x(x+1)=0,x﹣2≠0,
∴x≠0,﹣1,2,
∴x=﹣3,
∴原式=x+1
=﹣3+1
=﹣2.
19.(8分)解方程:
(1)8﹣2x2=0;
(2)x(2﹣x)=x﹣2.
【分析】(1)利用直接开平方法解方程;
(2)利用因式分解法解方程.
【解答】解:(1)原方程化简为x2=4,
∴x=±2,
∴x1=2,x2=﹣2;
(2)原方程可化为(x﹣2)(x+1)=0,
∴x﹣2=0或x+1=0,
∴x1=2,x2=﹣1.
20.(8分)如图,一次函数y=mx+n(m≠0)与反比例函数y=(k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积.
【分析】(1)把A点坐标代入反比例函数解析式可求得k,再把B点坐标代入可求得b,再利用待定系数法可求得一次函数解析式;
(2)可先求得D点坐标,再利用三角形的面积计算即可.
【解答】解:
(1)∵反比例函数y=(k≠0)的图象过A(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣,
当x=2时,y=﹣1,
即B点坐标为(2,﹣1),
∵一次函数y=mx+n(m≠0)过A、B两点,
∴把A、B两点坐标代入可得,解得,
∴一次函数解析式为y=﹣x+1;
(2)在y=﹣x+1中,当x=0时,y=1,
∴C点坐标为(0,1),
∵点D与点C关于x轴对称,
∴D点坐标为(0,﹣1),
∴CD=2,
∴S△ABD=S△ACD+S△BCD=×2×1+×2×2=3.
21.(8分)已知关于x的一元二次方程x2﹣mx﹣3=0.
(1)求证:无论m取何实数,该方程总有两个不相等的实数根;
(2)若方程的一根为3,求m的值及另一个根.
【分析】(1)根据方程的系数结合根的判别式即可得出Δ=m2+12≥12,由此即可得出结论.
(2)将x=3代入原方程求出m值,再将m的值代入原方程利用十字相乘法即可求出方程的另一根,或者直接利用两根之积等于﹣3可得.
【解答】(1)证明:∵在方程x2﹣mx﹣3=0中,Δ=(﹣m)2﹣4×1×(﹣3)=m2+12≥12,
∴对于任意实数m,方程总有两个不相等的实数根.
(2)解:方法一:将x=3代入x2﹣mx﹣3=0中,得:9﹣3m﹣3=0,
解得:m=2,
当m=2时,原方程为x2﹣2x﹣3=(x+1)(x﹣3)=0,
解得:x1=﹣1,x2=3,
∴方程的另一根为﹣1.
方法二:设方程的另一个根为a,
则3a=﹣3,
解得:a=﹣1,
即方程的另一根为﹣1.
22.(8分)为抗击疫情,人们众志成城,响应号召,口罩成了生活必需品,某药店销售普通口罩和N95口罩.
(1)计划N95口罩每包售价比普通口罩贵16元,14包普通口罩和6包N95口罩总售价相同,求普通口罩和N95口罩每包售价;
(2)已知普通口罩每包进价8元,按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包.该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天普通口罩的利润为320元,求此时普通口罩每包售价.
【分析】(1)设普通口罩每包的售价为x元,N95口罩每包的售价为y元,根据“N95口罩每包售价比普通口罩贵16元,14包普通口罩和6包N95口罩总售价相同”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设普通口罩每包的售价降低m元,则此时普通口罩每包的售价为(12﹣m)元,日均销售量为(120+20m)包,利用每天销售普通口罩的利润=销售每包普通口罩的利润×日均销售量,即可得出关于m的一元二次方程,解之取其正值即可得出m的值,再将其代入(12﹣m)中即可求出结论.
【解答】解:(1)设普通口罩每包的售价为x元,N95口罩每包的售价为y元,
依题意得:,
解得:.
答:普通口罩每包的售价为12元,N95口罩每包的售价为28元.
(2)设普通口罩每包的售价降低m元,则此时普通口罩每包的售价为(12﹣m)元,日均销售量为(120+20m)包,
依题意得:(12﹣m﹣8)(120+20m)=320,
整理得:m2+2m﹣8=0,
解得:m1=2,m2=﹣4(不合题意,舍去),
∴12﹣m=10.
答:此时普通口罩每包的售价为10元.
23.(10分)如图所示,四边形ABCD为矩形,AB=6cm,AD=4cm,若点Q从A点出发沿AD以1cm/s的速度向D运动,P从B点出发沿BA以2cm/s的速度向A运动,如果P、Q分别同时出发,当一个点到达终点时,另一点也同时停止.设运动的时间为t(s).
(1)当t为何值时,△PAQ为等腰三角形?
(2)当t为何值时,△APD的面积为6cm2?
(3)五边形PBCDQ的面积能否达到20cm2?若能,请求出t的值;若不能,请说明理由.
(4)当t为何值时,P、Q两点之间的距离为cm?
【分析】(1)由题意可得,AQ=tcm,BP=2tcm,AP=(6﹣2t)cm,根据△PAQ为等腰三角形,建立方程求解即可;
(2)根据S△APD=AD AP=12﹣4t=6,即可求得答案;
(3)根据S五边形PBCDQ=S矩形ABCD﹣S△APQ,可得t2﹣3t+4=0,利用根的判别式即可得出答案;
(4)运用勾股定理可得PQ==,由P、Q两点之间的距离为cm,建立方程求解即可.
【解答】解:(1)根据题意,AQ=tcm,BP=2tcm,AP=(6﹣2t)cm,
∵△PAQ为等腰三角形,∠A=90°,
∴AQ=AP,即t=6﹣2t,
解得:t=2,
∴当t=2时,△PAQ为等腰三角形.
(2)∵S△APD=AD AP=×4×(6﹣2t)=(12﹣4t)(cm2),
∴12﹣4t=6,
解得:t=,
∴当t=时,△APD的面积为6cm2.
(3)∵S五边形PBCDQ=S矩形ABCD﹣S△APQ=6×4﹣t(6﹣2t)=(24﹣3t+t2)(cm2),
∴24﹣3t+t2=20,
整理得:t2﹣3t+4=0,
∵△=(﹣3)2﹣4×1×4=﹣7<0,
∴该方程没有实数根,
∴五边形PBCDQ的面积不能达到20cm2.
(4)在Rt△APQ中,PQ==,
根据题意得:=2,
∴5t2﹣24t+16=0,
解得:t1=4,t2=,
∵6÷2=3,4÷1=4,
∴0≤t≤3,
∴t=.
24.(10分)如图1,点A(0,8)、点B(m,4)在直线y=﹣2x+n上,反比例函数(x>0)的图象经过点B.
(1)求m和k的值;
(2)将线段AB向右平移a个单位长度(a>0),得到对应线段CD,连接AC、BD.
①如图2,当a=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,则= .
②连接BC,在线段AB运动过程中,△ABC能否是等腰三角形,若能,求所有满足条件a的值,若不能,请说明理由.
【分析】(1)用待定系数法即可求出m和k的值;
(2)①根据线段AB向右平移3个单位得到CD,可以求出D的坐标,再根据反比例函数求出E的坐标,从而求出DE和DF;
②分BC=AB,BC=AC,AB=AC三种种情况讨论,分别列出对应的方程即可求解.
【解答】解:(1)∵点A(0,8)在直线y=﹣2x+n上,
∴﹣2×0+n=8,
∴n=8,
∴直线AB的解析式为y=﹣2x+8,
将点B(m,4)代入直线AB的解析式y=﹣2x+8上,得﹣2 m+8=4,
∴m=2,
∴B(2,4),
将B(2,4)代入反比例函数解析式中,得k=xy=2×4=8.
(2)①由(1)知,B(2,4),k=8,
∴反比例函数解析式为,
当a=3时,
∴将线段AB向右平移3个单位长度,得到对应线段CD,
∴D(2+3,4),
即:D(5,4),
∵DF⊥x轴于点F,交反比例函数图象于点E,
∴,
∴,,
∴;
故答案为:.
②如图,
∵将线段AB向右平移a个单位长度(a>0),得到对应线段CD,
∴CD=AB,AC=BD=a,
∵A(0,8),B(2,4),
∴C(a,8),
∵△ABC是等腰三角形,
∴Ⅰ、当BC=AB时,
∴点B在线段AC的垂直平分线上,
∴a=2×2=4.
Ⅱ、当BC=AC时,
∵B(2,4),C(a,8),
∴,
∴,
∴a=5,
Ⅲ、当AB=AC时,
∴,
即:△ABC是等腰三角形时,满足条件a的值为4或5或.
一、单选题(本大道题共8小题,每题3分,满分24分)
1.(3分)下列方程是一元二次方程的是( )
A.2xy+1=0 B.x﹣=1 C.x2=2 D.ax2+bx+c=0
2.(3分)对于反比例函数y=,下列说法中不正确的是( )
A.y随x的增大而减小
B.它的图象在第一、三象限
C.点(﹣3,﹣1)在它的图象上
D.函数图象关于原点中心对称
3.(3分)一元二次方程4x2﹣4x+1=0的根的情况是( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
4.(3分)方程x2﹣6x﹣10=0变形时,下列变形正确的是( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
5.(3分)已知点A(﹣2,y1),B(﹣4,y2)都在反比例函数y=(k>0)的图象上,则y1,y2的大小关系( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法确定
6.(3分)如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b>的解集为( )
A.x<﹣6 B.﹣6<x<0或x>2
C.x>2 D.x<﹣6或0<x<2
7.(3分)函数y=与y=kx+k在同一坐标系的图象大致是图中的( )
A. B.
C. D.
8.(3分)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴、y轴分别相交于点B,点A,以线段AB为边作正方形ABCD,且点C在反比例函数y=(x<0)的图象上,则k的值为( )
A.﹣10 B.﹣6 C.﹣20 D.20
二、填空题(本大道题共8小题,每题4分,满分32分)
9.(4分)已知点A(﹣3,2)在反比例函数y=的图象上,则k的值为 .
10.(4分)方程2x2﹣5=﹣6x化一般式为 .
11.(4分)若反比例函数y=的图象在每一象限内,y随x的增大而增大,则m的取值范围是 .
12.(4分)某果园2019年水果产量为100吨,2021年水果产量为144吨,则该果园水果产量的年平均增长率为 .
13.(4分)若方程3x2﹣5x﹣2=0有一根是a,则6a2﹣10a= .
14.(4分)如图,反比例函数y=(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作轴BE⊥x于点E,连接AD,已知AC=2,BE=2,S矩形BEOD=16,则S△ACD= .
15.(4分)中国民歌不仅脍炙人口,而且许多还有教育意义,有一首《牧童王小良》的民歌还包含着一个数学问题:
牧童王小良,放牧一群羊.问他羊几只,请你仔细想.头数加只数,只数减头数.只数乘头数,只数除头数.四数连加起,正好一百数.
如果设羊的只数为x,则根据民歌的大意,你能列出的方程是 .
16.(4分)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,
下列结论:
①BE+DF=EF;②CE=CF;③∠AEB=75°;④S正方形ABCD=2+,
其中正确的序号是 .
三、解答题(本大道题共8小题,满分64分)
17.(6分)当m为何值时,函数y=(m+3)x2﹣|m|是反比例函数?
18.(6分)先化简,再求值,其中x2+x﹣6=0.
19.(8分)解方程:
(1)8﹣2x2=0;
(2)x(2﹣x)=x﹣2.
20.(8分)如图,一次函数y=mx+n(m≠0)与反比例函数y=(k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积.
21.(8分)已知关于x的一元二次方程x2﹣mx﹣3=0.
(1)求证:无论m取何实数,该方程总有两个不相等的实数根;
(2)若方程的一根为3,求m的值及另一个根.
22.(8分)为抗击疫情,人们众志成城,响应号召,口罩成了生活必需品,某药店销售普通口罩和N95口罩.
(1)计划N95口罩每包售价比普通口罩贵16元,14包普通口罩和6包N95口罩总售价相同,求普通口罩和N95口罩每包售价;
(2)已知普通口罩每包进价8元,按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包.该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天普通口罩的利润为320元,求此时普通口罩每包售价.
23.(10分)如图所示,四边形ABCD为矩形,AB=6cm,AD=4cm,若点Q从A点出发沿AD以1cm/s的速度向D运动,P从B点出发沿BA以2cm/s的速度向A运动,如果P、Q分别同时出发,当一个点到达终点时,另一点也同时停止.设运动的时间为t(s).
(1)当t为何值时,△PAQ为等腰三角形?
(2)当t为何值时,△APD的面积为6cm2?
(3)五边形PBCDQ的面积能否达到20cm2?若能,请求出t的值;若不能,请说明理由.
(4)当t为何值时,P、Q两点之间的距离为cm?
24.(10分)如图1,点A(0,8)、点B(m,4)在直线y=﹣2x+n上,反比例函数(x>0)的图象经过点B.
(1)求m和k的值;
(2)将线段AB向右平移a个单位长度(a>0),得到对应线段CD,连接AC、BD.
①如图2,当a=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,则= .
②连接BC,在线段AB运动过程中,△ABC能否是等腰三角形,若能,求所有满足条件a的值,若不能,请说明理由.
2021-2022学年湖南省岳阳市岳阳县六校联考九年级(上)第一次月考数学试卷
参考答案与试题解析
一、单选题(本大道题共8小题,每题3分,满分24分)
1.(3分)下列方程是一元二次方程的是( )
A.2xy+1=0 B.x﹣=1 C.x2=2 D.ax2+bx+c=0
【分析】利用一元二次方程定义进行解答即可.
【解答】解:A、含有2个未知数,不是一元二次方程,故此选项不符合题意;
B、是分式方程,故此选项不符合题意;
C、是一元二次方程,故此选项符合题意;
D、当a=0时,该方程不是一元二次方程,故此选项不符合题意.
故选:C.
2.(3分)对于反比例函数y=,下列说法中不正确的是( )
A.y随x的增大而减小
B.它的图象在第一、三象限
C.点(﹣3,﹣1)在它的图象上
D.函数图象关于原点中心对称
【分析】根据题目中的函数解析式和反比例函数的性质,可以判断各个选项中的说法是否正确,本题得以解决.
【解答】解:∵反比例函数y=,
∴该函数图象在第一、三象限,故选项B正确;
在每个象限内,y随x的增大而减小,故选项A错误;
当x=﹣3时,y=﹣1,即点(﹣3,﹣1)在它的图象上,故选项C正确;
函数图象关于原点中心对称,故选项D正确;
故选:A.
3.(3分)一元二次方程4x2﹣4x+1=0的根的情况是( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
【分析】根据方程的系数结合根的判别式,可得出Δ=0,进而可得出一元二次方程4x2﹣4x+1=0有两个相等的实数根.
【解答】解:∵Δ=(﹣4)2﹣4×4×1=0,
∴一元二次方程4x2﹣4x+1=0有两个相等的实数根.
故选:C.
4.(3分)方程x2﹣6x﹣10=0变形时,下列变形正确的是( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
【分析】根据配方法即可求出答案.
【解答】解:∵x2﹣6x﹣10=0,
∴x2﹣6x=10,
∴x2﹣6x+9=19,
∴(x﹣3)2=19,
故选:D.
5.(3分)已知点A(﹣2,y1),B(﹣4,y2)都在反比例函数y=(k>0)的图象上,则y1,y2的大小关系( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法确定
【分析】直接利用反比例函数的增减性分析得出答案.
【解答】解:∵反比例函数y=(k>0)中,k>0,
∴在每个象限内,y随x的增大而减小,
∵点A(﹣2,y1),B(﹣4,y2)都在反比例函数y=(k>0)的图象上,且﹣2>﹣4
∴y1<y2,
故选:B.
6.(3分)如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b>的解集为( )
A.x<﹣6 B.﹣6<x<0或x>2
C.x>2 D.x<﹣6或0<x<2
【分析】根据函数的图象和交点坐标即可求得结果.
【解答】解:不等式kx+b>的解集为:﹣6<x<0或x>2,
故选:B.
7.(3分)函数y=与y=kx+k在同一坐标系的图象大致是图中的( )
A. B.
C. D.
【分析】因为k的符号不确定,所以应根据k的符号及一次函数与反比例函数图象的性质解答.
【解答】解:∵y=kx+k=k(x+1),
∴直线经过点(﹣1,0),故A、C选项错误;
当k<0时,反比例函数y=的图象在二,四象限,一次函数y=kx+k的图象过二、三、四象限,选项B、D不符合;
当k>0时,反比例函数y=的图象在一、三象限,一次函数y=kx+k的图象过一、二、三象限,选项B符合.
故选:B.
8.(3分)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴、y轴分别相交于点B,点A,以线段AB为边作正方形ABCD,且点C在反比例函数y=(x<0)的图象上,则k的值为( )
A.﹣10 B.﹣6 C.﹣20 D.20
【分析】过点C作CE⊥x轴于E,证明△AOB≌△BEC,可得点C坐标,代入求解即可.
【解答】解:∵当x=0时,y=×0+3=3,
∴A(0,3),
∴OA=3;
∵当y=0时,0=x+3,
∴x=﹣2,
∴B(﹣2,0),
∴OB=2;
过点C作CE⊥x轴于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠CBE+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
在△AOB和△BEC中,
,
∴△AOB≌△BEC(AAS),
∴BE=AO=3,CE=OB=2,
∴OE=3+2=5,
∴C点坐标为(﹣5,2),
∵点C在反比例函数y=(x<0)的图象上,
∴k=﹣5×2=﹣10.
故选:A.
二、填空题(本大道题共8小题,每题4分,满分32分)
9.(4分)已知点A(﹣3,2)在反比例函数y=的图象上,则k的值为 ﹣6 .
【分析】根据点A的坐标,利用反比例函数图象上点的坐标特征求出k值,此题得解.
【解答】解:∵点A(﹣3,2)在反比例函数y=的图象上,
∴k=(﹣3)×2=﹣6.
故答案为:﹣6.
10.(4分)方程2x2﹣5=﹣6x化一般式为 2x2+6x﹣5=0 .
【分析】移项后即可得出一元二次方程的一般形式.
【解答】解:2x2﹣5=﹣6x,
移项,得2x2+6x﹣5=0,
故答案为:2x2+6x﹣5=0.
11.(4分)若反比例函数y=的图象在每一象限内,y随x的增大而增大,则m的取值范围是 m<﹣2 .
【分析】根据反比例函数的性质得到m+2<0,然后解一元一次不等式即可.
【解答】解:根据题意得m+2<0,
解得m<﹣2.
故答案为m<﹣2.
12.(4分)某果园2019年水果产量为100吨,2021年水果产量为144吨,则该果园水果产量的年平均增长率为 20% .
【分析】可根据二次增长公式a(1+x)2=b,列出以增长率为未知数的方程,求出增长率.
【解答】解:设该果园水果产量的年平均增长率为x,根据题意,得
100(1+x)2=144,
解方程得x1=0.2,x2=﹣2.2.x2=﹣2.2不符合题意,舍去.
故答案为20%.
13.(4分)若方程3x2﹣5x﹣2=0有一根是a,则6a2﹣10a= 4 .
【分析】将a代入方程3x2﹣5x﹣2=0,得到3a2﹣5a=2,等式的两边都扩大为原来的2倍,问题可求.
【解答】解:由题意,把是a的根代入3x2﹣5x﹣2=0,
得:3a2﹣5a=2,
∴2×(3a2﹣5a)=2×2,
∴6a2﹣10a=4.
14.(4分)如图,反比例函数y=(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作轴BE⊥x于点E,连接AD,已知AC=2,BE=2,S矩形BEOD=16,则S△ACD= 6 .
【分析】利用反比例函数比例系数k的几何意义得到S矩形BEOD=|k|=16,则求出k得到反比例函数的解析式为y=,再利用A点的横坐标为2可计算出A点的纵坐标为8,从而得到CD=6,然后根据三角形面积公式计算S△ACD.
【解答】解:∵BE⊥x轴于E,BD⊥y轴于D,
∴S矩形BEOD=|k|=16,
而k<0,
∴k=16,
∴反比例函数的解析式为y=,
∵AC⊥y轴,AC=2,
∴A点的横坐标为2,
当x=2时,y==8,
∴CD=OC﹣OD=8﹣2=6,
∴S△ACD=×2×6=6.
故答案为6.
15.(4分)中国民歌不仅脍炙人口,而且许多还有教育意义,有一首《牧童王小良》的民歌还包含着一个数学问题:
牧童王小良,放牧一群羊.问他羊几只,请你仔细想.头数加只数,只数减头数.只数乘头数,只数除头数.四数连加起,正好一百数.
如果设羊的只数为x,则根据民歌的大意,你能列出的方程是 x2+2x+1=100 .
【分析】等量关系为:头数加只数+只数减头数+只数乘头数+只数除头数=100,把相关数值代入化简即可.
【解答】解:∵羊的只数为x,
∴头数加只数为2x,只数减头数为0.只数乘头数为x2,只数除头数为1,
∴可列方程为:x2+2x+1=100,
故答案为:x2+2x+1=100.
16.(4分)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,
下列结论:
①BE+DF=EF;②CE=CF;③∠AEB=75°;④S正方形ABCD=2+,
其中正确的序号是 ②③④ .
【分析】由正方形的性质得AB=AD,∠B=∠D=90°,由等边三角形的性质得AE=AF,则可判断Rt△ABE≌△ADF,得到BE=DF,∠BAE=∠DAF,加上∠EAF=60°,易得∠BAE=∠DAF=15°,利用互余得∠AEB=75°,则可对③进行判断;由于CB=CD,BE=DF,则CE=CF,于是可对②进行判断;先判断△CEF为等腰直角三角形得到CE=CF=EF=,设正方形的边长为x,则AB=x,BE=x﹣,在Rt△ABE中利用勾股定理得x2+(x﹣)2=22,解得x1=,x2=(舍去),则可计算出BE+DF=﹣,于是可判断①错误;然后利用正方形面积公式可对④进行判断.
【解答】解:∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°,
∵△AEF为等边三角形,
∴AE=AF,
在Rt△ABE和△ADF中,
,
∴Rt△ABE≌△ADF,
∴BE=DF,∠BAE=∠DAF,
而∠EAF=60°,
∴∠BAE=∠DAF=15°,
∴∠AEB=75°,所以③正确,
∵CB=CD,
∴CB﹣BE=CD﹣DF,
即CE=CF,所以②正确;
∴△CEF为等腰直角三角形,
∴CE=CF=EF=,
设正方形的边长为x,则AB=x,BE=x﹣,
在Rt△ABE中,∵AB2+BE2=AE2,
∴x2+(x﹣)2=22,
整理得x2﹣x﹣1=0,解得x1=,x2=(舍去),
∴BE+DF=2(x﹣)=2(﹣)=﹣≠2,所以①错误;
∴S正方形ABCD=x2=()2=2+,所以④正确.
对于①的判断可用下面的方法:
连接AC交EF于G,如图,
∵AE=AF,CE=CF,
∴AC垂直平分EF,
∴EG=FG,
∵∠BAE=15°,∠GAE=30°,
∴BE=AE sin15°,EG=AE sin30°,
∴BE≠EG,
∴BE+DF≠EF,所以①错误.
故答案为②③④.
三、解答题(本大道题共8小题,满分64分)
17.(6分)当m为何值时,函数y=(m+3)x2﹣|m|是反比例函数?
【分析】根据反比例函数的定义得出2﹣|m|=﹣1且m+3≠0,再求出m即可.
【解答】解:∵函数y=(m+3)x2﹣|m|是反比例函数,
∴2﹣|m|=﹣1且m+3≠0,
解得:m=3,
即当m=3时,函数y=(m+3)x2﹣|m|是反比例函数.
18.(6分)先化简,再求值,其中x2+x﹣6=0.
【分析】先按照分式乘除法法则化简计算,再解一元二次方程求解x值,后代入计算可求解.
【解答】解:原式=
=x+1,
∵x2+x﹣6=0,
∴x1=﹣3,x2=2,
∵x(x+1)=0,x﹣2≠0,
∴x≠0,﹣1,2,
∴x=﹣3,
∴原式=x+1
=﹣3+1
=﹣2.
19.(8分)解方程:
(1)8﹣2x2=0;
(2)x(2﹣x)=x﹣2.
【分析】(1)利用直接开平方法解方程;
(2)利用因式分解法解方程.
【解答】解:(1)原方程化简为x2=4,
∴x=±2,
∴x1=2,x2=﹣2;
(2)原方程可化为(x﹣2)(x+1)=0,
∴x﹣2=0或x+1=0,
∴x1=2,x2=﹣1.
20.(8分)如图,一次函数y=mx+n(m≠0)与反比例函数y=(k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积.
【分析】(1)把A点坐标代入反比例函数解析式可求得k,再把B点坐标代入可求得b,再利用待定系数法可求得一次函数解析式;
(2)可先求得D点坐标,再利用三角形的面积计算即可.
【解答】解:
(1)∵反比例函数y=(k≠0)的图象过A(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣,
当x=2时,y=﹣1,
即B点坐标为(2,﹣1),
∵一次函数y=mx+n(m≠0)过A、B两点,
∴把A、B两点坐标代入可得,解得,
∴一次函数解析式为y=﹣x+1;
(2)在y=﹣x+1中,当x=0时,y=1,
∴C点坐标为(0,1),
∵点D与点C关于x轴对称,
∴D点坐标为(0,﹣1),
∴CD=2,
∴S△ABD=S△ACD+S△BCD=×2×1+×2×2=3.
21.(8分)已知关于x的一元二次方程x2﹣mx﹣3=0.
(1)求证:无论m取何实数,该方程总有两个不相等的实数根;
(2)若方程的一根为3,求m的值及另一个根.
【分析】(1)根据方程的系数结合根的判别式即可得出Δ=m2+12≥12,由此即可得出结论.
(2)将x=3代入原方程求出m值,再将m的值代入原方程利用十字相乘法即可求出方程的另一根,或者直接利用两根之积等于﹣3可得.
【解答】(1)证明:∵在方程x2﹣mx﹣3=0中,Δ=(﹣m)2﹣4×1×(﹣3)=m2+12≥12,
∴对于任意实数m,方程总有两个不相等的实数根.
(2)解:方法一:将x=3代入x2﹣mx﹣3=0中,得:9﹣3m﹣3=0,
解得:m=2,
当m=2时,原方程为x2﹣2x﹣3=(x+1)(x﹣3)=0,
解得:x1=﹣1,x2=3,
∴方程的另一根为﹣1.
方法二:设方程的另一个根为a,
则3a=﹣3,
解得:a=﹣1,
即方程的另一根为﹣1.
22.(8分)为抗击疫情,人们众志成城,响应号召,口罩成了生活必需品,某药店销售普通口罩和N95口罩.
(1)计划N95口罩每包售价比普通口罩贵16元,14包普通口罩和6包N95口罩总售价相同,求普通口罩和N95口罩每包售价;
(2)已知普通口罩每包进价8元,按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包.该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天普通口罩的利润为320元,求此时普通口罩每包售价.
【分析】(1)设普通口罩每包的售价为x元,N95口罩每包的售价为y元,根据“N95口罩每包售价比普通口罩贵16元,14包普通口罩和6包N95口罩总售价相同”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设普通口罩每包的售价降低m元,则此时普通口罩每包的售价为(12﹣m)元,日均销售量为(120+20m)包,利用每天销售普通口罩的利润=销售每包普通口罩的利润×日均销售量,即可得出关于m的一元二次方程,解之取其正值即可得出m的值,再将其代入(12﹣m)中即可求出结论.
【解答】解:(1)设普通口罩每包的售价为x元,N95口罩每包的售价为y元,
依题意得:,
解得:.
答:普通口罩每包的售价为12元,N95口罩每包的售价为28元.
(2)设普通口罩每包的售价降低m元,则此时普通口罩每包的售价为(12﹣m)元,日均销售量为(120+20m)包,
依题意得:(12﹣m﹣8)(120+20m)=320,
整理得:m2+2m﹣8=0,
解得:m1=2,m2=﹣4(不合题意,舍去),
∴12﹣m=10.
答:此时普通口罩每包的售价为10元.
23.(10分)如图所示,四边形ABCD为矩形,AB=6cm,AD=4cm,若点Q从A点出发沿AD以1cm/s的速度向D运动,P从B点出发沿BA以2cm/s的速度向A运动,如果P、Q分别同时出发,当一个点到达终点时,另一点也同时停止.设运动的时间为t(s).
(1)当t为何值时,△PAQ为等腰三角形?
(2)当t为何值时,△APD的面积为6cm2?
(3)五边形PBCDQ的面积能否达到20cm2?若能,请求出t的值;若不能,请说明理由.
(4)当t为何值时,P、Q两点之间的距离为cm?
【分析】(1)由题意可得,AQ=tcm,BP=2tcm,AP=(6﹣2t)cm,根据△PAQ为等腰三角形,建立方程求解即可;
(2)根据S△APD=AD AP=12﹣4t=6,即可求得答案;
(3)根据S五边形PBCDQ=S矩形ABCD﹣S△APQ,可得t2﹣3t+4=0,利用根的判别式即可得出答案;
(4)运用勾股定理可得PQ==,由P、Q两点之间的距离为cm,建立方程求解即可.
【解答】解:(1)根据题意,AQ=tcm,BP=2tcm,AP=(6﹣2t)cm,
∵△PAQ为等腰三角形,∠A=90°,
∴AQ=AP,即t=6﹣2t,
解得:t=2,
∴当t=2时,△PAQ为等腰三角形.
(2)∵S△APD=AD AP=×4×(6﹣2t)=(12﹣4t)(cm2),
∴12﹣4t=6,
解得:t=,
∴当t=时,△APD的面积为6cm2.
(3)∵S五边形PBCDQ=S矩形ABCD﹣S△APQ=6×4﹣t(6﹣2t)=(24﹣3t+t2)(cm2),
∴24﹣3t+t2=20,
整理得:t2﹣3t+4=0,
∵△=(﹣3)2﹣4×1×4=﹣7<0,
∴该方程没有实数根,
∴五边形PBCDQ的面积不能达到20cm2.
(4)在Rt△APQ中,PQ==,
根据题意得:=2,
∴5t2﹣24t+16=0,
解得:t1=4,t2=,
∵6÷2=3,4÷1=4,
∴0≤t≤3,
∴t=.
24.(10分)如图1,点A(0,8)、点B(m,4)在直线y=﹣2x+n上,反比例函数(x>0)的图象经过点B.
(1)求m和k的值;
(2)将线段AB向右平移a个单位长度(a>0),得到对应线段CD,连接AC、BD.
①如图2,当a=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,则= .
②连接BC,在线段AB运动过程中,△ABC能否是等腰三角形,若能,求所有满足条件a的值,若不能,请说明理由.
【分析】(1)用待定系数法即可求出m和k的值;
(2)①根据线段AB向右平移3个单位得到CD,可以求出D的坐标,再根据反比例函数求出E的坐标,从而求出DE和DF;
②分BC=AB,BC=AC,AB=AC三种种情况讨论,分别列出对应的方程即可求解.
【解答】解:(1)∵点A(0,8)在直线y=﹣2x+n上,
∴﹣2×0+n=8,
∴n=8,
∴直线AB的解析式为y=﹣2x+8,
将点B(m,4)代入直线AB的解析式y=﹣2x+8上,得﹣2 m+8=4,
∴m=2,
∴B(2,4),
将B(2,4)代入反比例函数解析式中,得k=xy=2×4=8.
(2)①由(1)知,B(2,4),k=8,
∴反比例函数解析式为,
当a=3时,
∴将线段AB向右平移3个单位长度,得到对应线段CD,
∴D(2+3,4),
即:D(5,4),
∵DF⊥x轴于点F,交反比例函数图象于点E,
∴,
∴,,
∴;
故答案为:.
②如图,
∵将线段AB向右平移a个单位长度(a>0),得到对应线段CD,
∴CD=AB,AC=BD=a,
∵A(0,8),B(2,4),
∴C(a,8),
∵△ABC是等腰三角形,
∴Ⅰ、当BC=AB时,
∴点B在线段AC的垂直平分线上,
∴a=2×2=4.
Ⅱ、当BC=AC时,
∵B(2,4),C(a,8),
∴,
∴,
∴a=5,
Ⅲ、当AB=AC时,
∴,
即:△ABC是等腰三角形时,满足条件a的值为4或5或.
同课章节目录
