鲁教版(五四学制)七年级上册第一章 三角形1.4三角形的尺规作图课件(共21张PPT)
文档属性
| 名称 | 鲁教版(五四学制)七年级上册第一章 三角形1.4三角形的尺规作图课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 427.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 15:54:33 | ||
图片预览





文档简介
(共21张PPT)
4.4 用尺规作三角形
1、尺规作图的工具是直尺和圆规
2、我们已经会用尺规作一条线段等于已知线段、作一个角等于已知角
复习引入
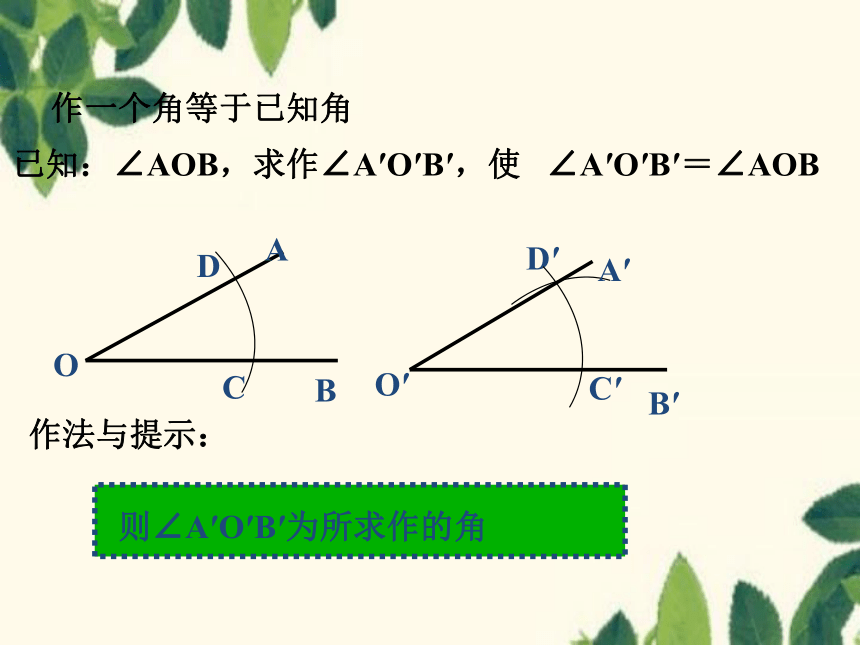
已知:∠AOB,求作∠A′O′B′,使 ∠A′O′B′=∠AOB
O
B
A
C
D
O′
B′
A′
D′
C′
则∠A′O′B′为所求作的角
作法与提示:
作一个角等于已知角
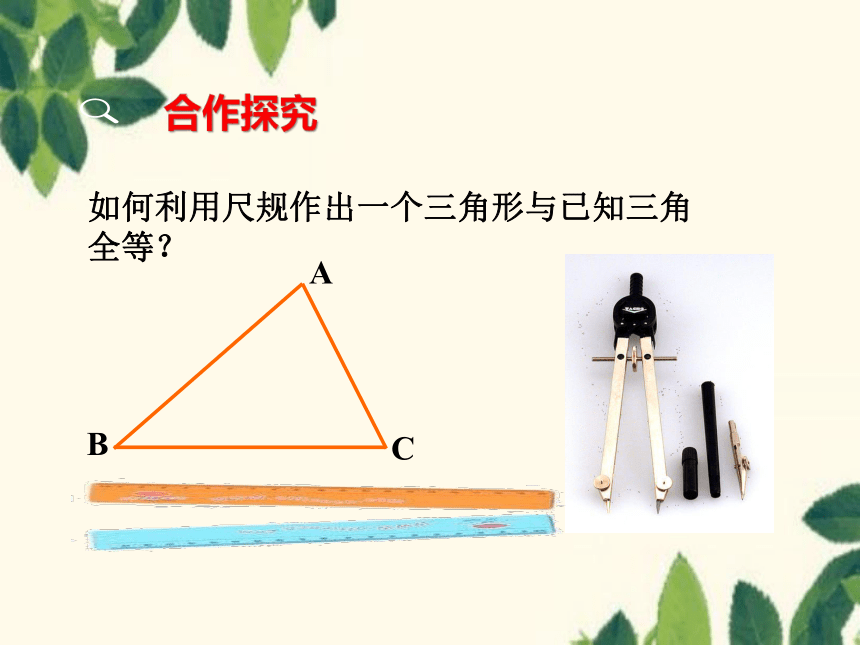
如何利用尺规作出一个三角形与已知三角
全等?
A
B
C
合作探究
已知三角形的两边及其夹角,求作这个三角形.
已知:线段a, c, .
求作:△ABC,使BC=a AB=c, ∠ABC= .
a
c
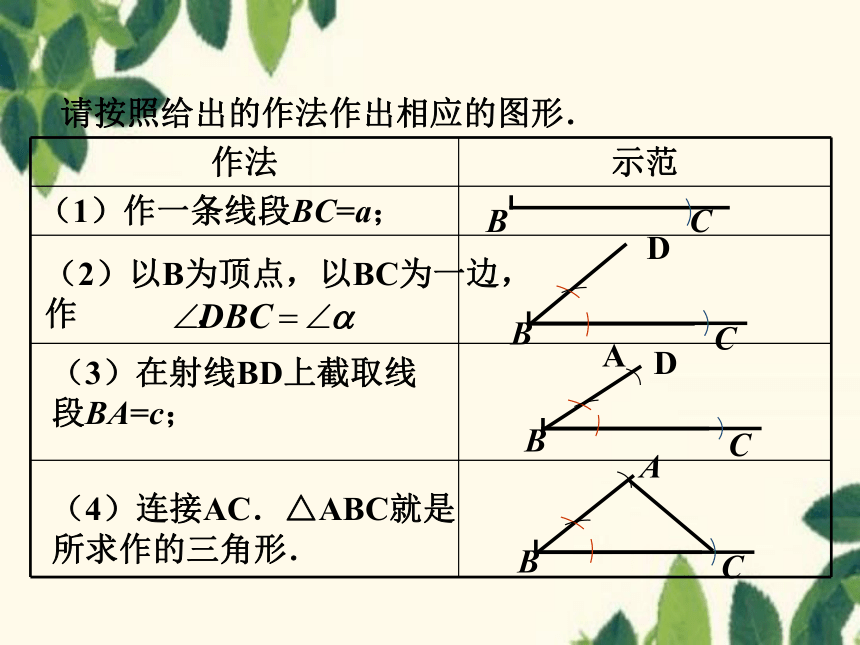
作法 示范
(1)作一条线段BC=a;
(2)以B为顶点,以BC为一边,作 .
B
C
B
C
B
C
B
C
(3)在射线BD上截取线段BA=c;
(4)连接AC.△ABC就是所求作的三角形.
A
D
D
A
请按照给出的作法作出相应的图形.
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
两边及它们的夹角对应相等的两个三角形全等(SAS)
已知三角形的两边及夹角,求作这个三角形。
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
还有没有其他的作法?
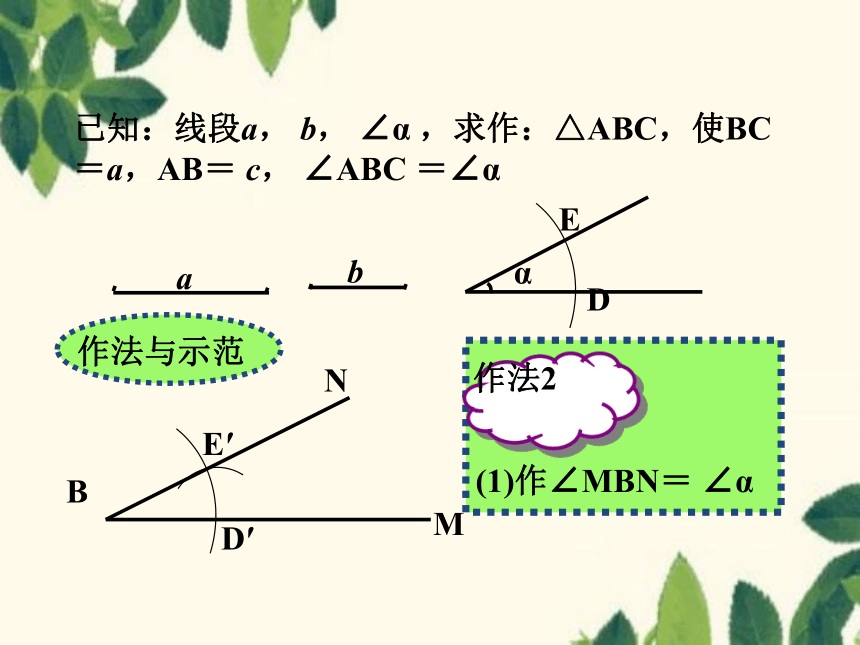
已知:线段a, b, ∠α ,求作:△ABC,使BC=a,AB= c, ∠ABC =∠α
a
b
α
B
M
D
E
D′
E′
N
(1)作∠MBN= ∠α
作法2
作法与示范
B
M
D′
E′
N
C
A
(2)在射线B M上截取BC=a,
在射线B N上截取BA=b,
作法2
作法与示范
a
b
B
M
D′
E′
N
C
A
(3)连接AC
则△ABC为所求作的三角形
作法2
作法与示范
a
b
已知三角形的两角及其夹边,求作这个三角形.
已知: , ,线段c.
c
求作:△ABC,使∠A= ,∠B= ,AB=c.
已知: , ,线段c.
c
求作:△ABC,使∠A= ,∠B= ,AB=c.
c
请按照给出的作法作出相应的图形.
作法 示范
(1)作 .
A
F
(2)在射线AF上截取线段AB=c;
C
D
B
A
D
F
A
B
D
F
(3)以B为顶点,以BA为一边,作 ,BE交AD于点C.则△ABC就是所求作的三角形.
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
两角及它们的夹边对应相等的两个三角形全等(ASA)
已知三角形的两角及其夹边,求作这个三角形。
回顾刚才作三角形的顺序
角
角
夹边
夹边
角
角
还有没有其他的作法?
已知:∠α, ∠β, 线段c,
求作:△ABC,使∠A=∠α,∠B=∠β,AB= c
β
c
作法示范
作法:(1)作线段 AB= c
A
M
A
M
B
(2)作∠NAB=∠α,
N
K
C
(3)作∠KBA=∠β
AN与BK相交于C,则△ABC为所求作的三角形
α
经过前面的实践,我们如何来分析作图题呢?
1. 假设所求作的图形已经作出,并在草稿纸上作出草图;
2. 在草图上标出已给的边、角的对应位置;
3. 从草图中首先找出基本图形,由此确定作图的起始步骤;
4. 在3的基础上逐步向所求图形扩展。
课堂小结
(1)作∠······=∠ ······ ;
(2)在······上截取,使······ = ······ ;
(3)以···为顶点,以······为一边,作∠ ······ =∠ ······ ;
(4)作一条线段······ = ······ ;
(5)连接······ ,或连接······交······于点······ ;
(6)分别以··· , ···为圆心,以··· , ···为半径画弧,两弧交于···点;
······ ······ ······ ······
你知道的常用作图语言有哪些呢?
1.已知三角形的三边,求作这个三角形.
已知:线段a,b,c.
a
c
b
求作:△ABC,使AB=c,AC=b,BC=a.
(1)请写出作法并作出相应的图形.
(2)将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
巩固训练
2.已知三角形的三条边,求作这个三角形。
已知:线段 a,b,c。
求作:△ABC,使AB=c,AC=b,BC=a。
(1)作一条线段BC=a;
(2)分别以B,C为圆心,以c,b为半径画弧,两弧交于A点;
(3)连接AB,AC。
△ABC就是所求作的三角形。
a
b
c
B
C
A
作法:
4.4 用尺规作三角形
1、尺规作图的工具是直尺和圆规
2、我们已经会用尺规作一条线段等于已知线段、作一个角等于已知角
复习引入
已知:∠AOB,求作∠A′O′B′,使 ∠A′O′B′=∠AOB
O
B
A
C
D
O′
B′
A′
D′
C′
则∠A′O′B′为所求作的角
作法与提示:
作一个角等于已知角
如何利用尺规作出一个三角形与已知三角
全等?
A
B
C
合作探究
已知三角形的两边及其夹角,求作这个三角形.
已知:线段a, c, .
求作:△ABC,使BC=a AB=c, ∠ABC= .
a
c
作法 示范
(1)作一条线段BC=a;
(2)以B为顶点,以BC为一边,作 .
B
C
B
C
B
C
B
C
(3)在射线BD上截取线段BA=c;
(4)连接AC.△ABC就是所求作的三角形.
A
D
D
A
请按照给出的作法作出相应的图形.
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
两边及它们的夹角对应相等的两个三角形全等(SAS)
已知三角形的两边及夹角,求作这个三角形。
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
还有没有其他的作法?
已知:线段a, b, ∠α ,求作:△ABC,使BC=a,AB= c, ∠ABC =∠α
a
b
α
B
M
D
E
D′
E′
N
(1)作∠MBN= ∠α
作法2
作法与示范
B
M
D′
E′
N
C
A
(2)在射线B M上截取BC=a,
在射线B N上截取BA=b,
作法2
作法与示范
a
b
B
M
D′
E′
N
C
A
(3)连接AC
则△ABC为所求作的三角形
作法2
作法与示范
a
b
已知三角形的两角及其夹边,求作这个三角形.
已知: , ,线段c.
c
求作:△ABC,使∠A= ,∠B= ,AB=c.
已知: , ,线段c.
c
求作:△ABC,使∠A= ,∠B= ,AB=c.
c
请按照给出的作法作出相应的图形.
作法 示范
(1)作 .
A
F
(2)在射线AF上截取线段AB=c;
C
D
B
A
D
F
A
B
D
F
(3)以B为顶点,以BA为一边,作 ,BE交AD于点C.则△ABC就是所求作的三角形.
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
两角及它们的夹边对应相等的两个三角形全等(ASA)
已知三角形的两角及其夹边,求作这个三角形。
回顾刚才作三角形的顺序
角
角
夹边
夹边
角
角
还有没有其他的作法?
已知:∠α, ∠β, 线段c,
求作:△ABC,使∠A=∠α,∠B=∠β,AB= c
β
c
作法示范
作法:(1)作线段 AB= c
A
M
A
M
B
(2)作∠NAB=∠α,
N
K
C
(3)作∠KBA=∠β
AN与BK相交于C,则△ABC为所求作的三角形
α
经过前面的实践,我们如何来分析作图题呢?
1. 假设所求作的图形已经作出,并在草稿纸上作出草图;
2. 在草图上标出已给的边、角的对应位置;
3. 从草图中首先找出基本图形,由此确定作图的起始步骤;
4. 在3的基础上逐步向所求图形扩展。
课堂小结
(1)作∠······=∠ ······ ;
(2)在······上截取,使······ = ······ ;
(3)以···为顶点,以······为一边,作∠ ······ =∠ ······ ;
(4)作一条线段······ = ······ ;
(5)连接······ ,或连接······交······于点······ ;
(6)分别以··· , ···为圆心,以··· , ···为半径画弧,两弧交于···点;
······ ······ ······ ······
你知道的常用作图语言有哪些呢?
1.已知三角形的三边,求作这个三角形.
已知:线段a,b,c.
a
c
b
求作:△ABC,使AB=c,AC=b,BC=a.
(1)请写出作法并作出相应的图形.
(2)将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
巩固训练
2.已知三角形的三条边,求作这个三角形。
已知:线段 a,b,c。
求作:△ABC,使AB=c,AC=b,BC=a。
(1)作一条线段BC=a;
(2)分别以B,C为圆心,以c,b为半径画弧,两弧交于A点;
(3)连接AB,AC。
△ABC就是所求作的三角形。
a
b
c
B
C
A
作法:
