13.3.1等腰三角形 练习题 2021—2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 13.3.1等腰三角形 练习题 2021—2022学年人教版八年级数学上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 441.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 00:00:00 | ||
图片预览



文档简介
2021——2022学年度人教版八年级数学上册 第十三章轴对称 13.3.1等腰三角形 练习题
一、选择题
1.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAC=5∠BAE,则∠C的度数为( )
A.30° B.40° C.50° D.60°
2.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线一点,点E在BC上,且AE=CF,∠CAE=30°,则∠ACF的度数是( )
A.75° B.60° C.55° D.45°
3.如图,在Rt△ABC中,∠ACB=90°.根据尺规作图痕迹,下列结论一定正确的是( )
A.BC=EC B.BE=EC C.BC=BE D.AE=EC
4.如图,在中,,于点 ,点是内一点,连接交于点 ,已知,若点是的内心,则 的度数为( )
A.36° B.48° C.60° D.72°
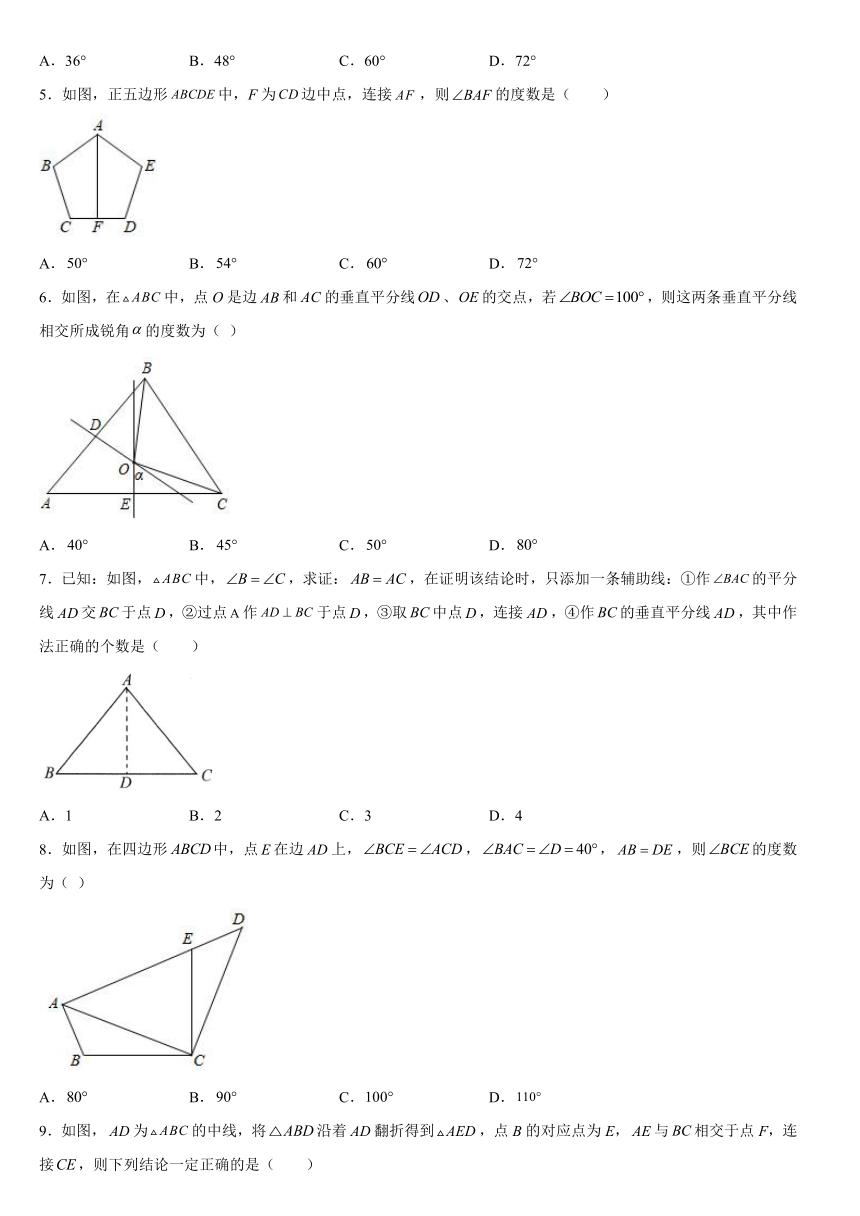
5.如图,正五边形中,F为边中点,连接,则的度数是( )
A. B. C. D.
6.如图,在中,点O是边和的垂直平分线、的交点,若,则这两条垂直平分线相交所成锐角的度数为( )
A. B. C. D.
7.已知:如图,中,,求证:,在证明该结论时,只添加一条辅助线:①作的平分线交于点,②过点作于点,③取中点,连接,④作的垂直平分线,其中作法正确的个数是( )
A.1 B.2 C.3 D.4
8.如图,在四边形中,点在边上,,,,则的度数为( )
A. B. C. D.
9.如图,为的中线,将沿着翻折得到,点B的对应点为E,与相交于点F,连接,则下列结论一定正确的是( )
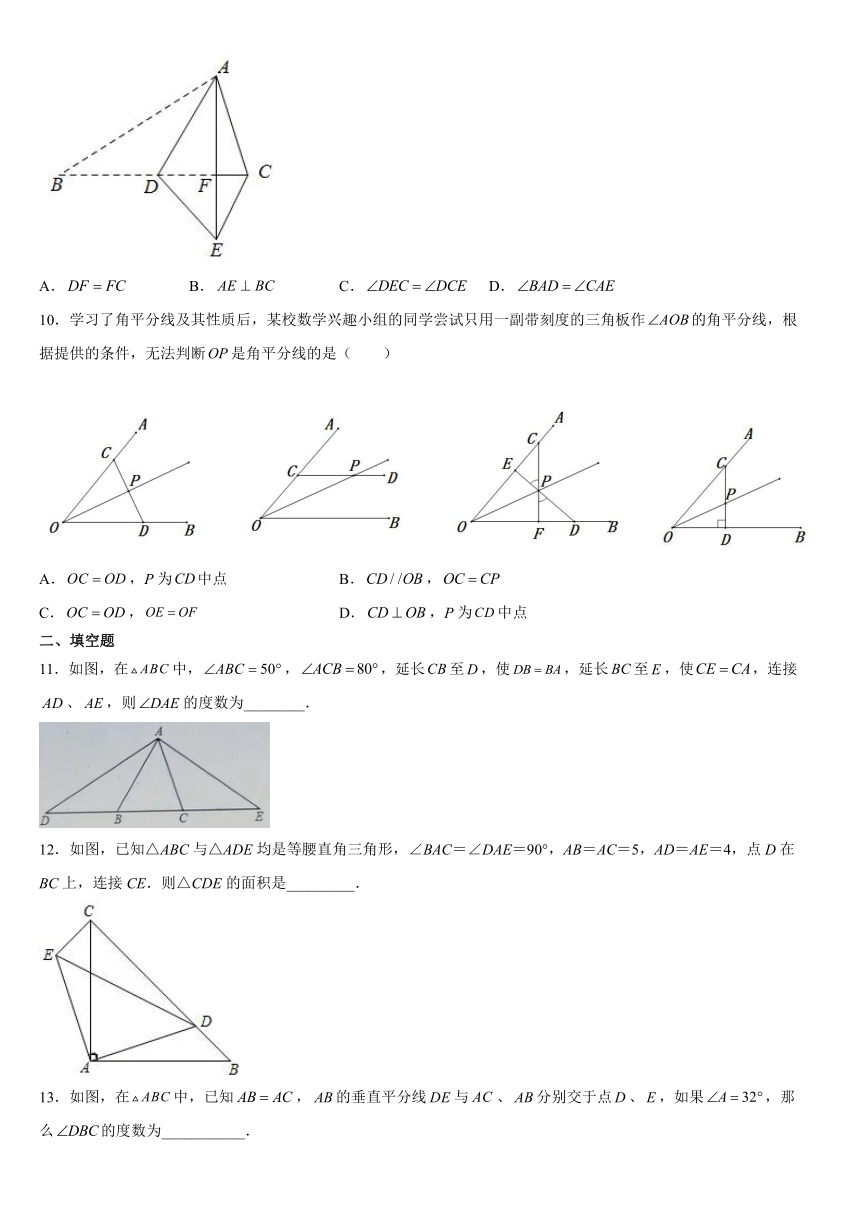
A. B. C. D.
10.学习了角平分线及其性质后,某校数学兴趣小组的同学尝试只用一副带刻度的三角板作的角平分线,根据提供的条件,无法判断是角平分线的是( )
A.,P为中点 B.,
C., D.,P为中点
二、填空题
11.如图,在中,,,延长至,使,延长至,使,连接、,则的度数为________.
12.如图,已知△ABC与△ADE均是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=5,AD=AE=4,点D在BC上,连接CE.则△CDE的面积是_________.
13.如图,在中,已知,的垂直平分线与、分别交于点、,如果,那么的度数为___________.
14.在等腰三角形ABC中,AB=AC,AC边上的中垂线交BC边于点D,垂足为E点,∠ABC的平分线交AC边于点F,交DE于点G,连接AD交BF于点H.则下列结论正确的是______.
①C△ABD=AC+BC(C表示周长);
②AH=DH;
③若AB=DB,则∠C=36°;
④若BD=CD,则图中有6个等腰三角形;
⑤若∠BDE=α,则∠BAC=360°﹣2α.
15.如图,四边形ABCD中,E是DC的中点,连接AE,AE平分∠DAB,∠D=∠C=90°,AD=4BC=8,则线段AB的长为__.
三、解答题
16.已知,,,F是CD的中点,求证:.
17.如图,在中,平分,,求证:.
18.如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM.
(1)求证:△AEF是等腰三角形;
(2)求证:DF=DN.
19.如图,在四边形ABCD中,AD // BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且GD=GF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系,并说明理由.
20.如图 ,与为等腰直角三角形,,,,,,连接、.
(1) 如图1 ,求证:△ACD≌△BCE ;
(2) 如图2 ,若、、三点共线,与交于点,且,,求的面积.
21.如图1,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,M、N分别在AB、AC上运动,且满足∠MDN=90°,
(1)试探究DM和DN有何数量关系,并证明.
(2)若M、N分别运动到BA、AC的延长线时,(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由.
22.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若,求的度数.
23.如图1,为测量池塘宽度,可在池塘外的空地上取任意一点,连接、,并分别延长至点,,使,,连接.
(1)求证:;
(2)如图2,受地形条件的影响,于是采取以下措施:延长至点,使,过点作的平行线,延长至点,连接,测得,,,,请直接写出池塘宽度.
【参考答案】
1.B 2.B 3.C 4.B 5.B 6.C 7.B 8.C 9.C 10.D
11.
12.
13.
14.①③⑤
15.10
16.解:如图,连接、,
在和中,
,
.
.
是等腰三角形.
又点是的中点,
,
∴△ACF≌△ADF(SSS),
,
.
17.证明:在上截取,连接,
∵平分
∴
又∵,
∴,
∴,,
可得
∴
∴
18.(1)解:∵∠BAC=90°,AB=AC,AD⊥BC,
∴∠ABC=∠ACB=∠BAD=∠CAD=45°,AD=BD=CD=BC,
∵∠ABC的平分线是BE,
∴∠ABE=∠CBE=∠ABC=22.5°,
∴∠AFE=∠BAD+∠ABE=45°+22.5°=67.5°,
∠AEF=∠ACB+∠CBE=45°+22.5°=67.5°,
∴∠AEF=∠AFE,
∴AF=AE,
∴△AEF是等腰三角形
(2)证明:∵AF=AE,M为EF的中点,∠CAD=45°,
∴∠CAN=∠CAD=22.5°,
∵AD⊥BC,
∴∠BDF=∠ADN=90°,
∵∠AND=∠ACB+∠CAN=45°+22.5°=67.5°,
又∵∠BFD=∠AFE=67.5°,
∴∠BFD=∠AND,
在△BDF和△ADN中
,
∴△BDF≌△ADN(AAS).
∴DF=DN
19.解:(1)如图1,
∵E是AB的中点,
∴AE=BE,
∵AD∥BC,
∴∠A=∠ABF,∠ADE=∠F,
∴△ADE≌△BFE;
(2)如图2,EG⊥DF;
理由是:由(1)得:△ADE≌△BFE,
∴DE=EF,
∵DG=FG,
∴线段EG是等腰三角形DFG的中线,也是高,
∴EG⊥FD;
20.解:(1),都是等腰直角三角形,
,,,
∴
,
在和中,
,
∴△ACD≌△BCE(SAS),
(2)如图2中,过点作于,
,都是等腰直角三角形,
,,,
,
∴△ACD≌△BCE(SAS),
,,
,
,
,
在和中,
,
∴△CQF≌△BEF(AAS),
,,
,
,
.
21.解:(1)DM=DN,
理由:连接AD,
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵D为BC中点,
∴,,∠ADC=90°,
∴∠C=∠BAD,
∵∠ADM+∠AND=∠MDN=90°,∠ADN+∠CDN=90°,
∴∠ADM=∠CDN,
在△AMD和△CND中,
,
∴△AMD≌△CND(ASA),
∴DM=DN;
(2)DM=DN仍然成立,
理由:连接AD,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵D为BC中点,
∴,,∠ADC=90°,
∴∠ACB=∠BAD=∠CAD=45°,
∵∠ADM+∠MDC=90°,∠MDC+∠CDN=90°,
∴∠ADM=∠CDN,
∵∠MAD=MAC+DAC=135°,∠NCD=180°﹣∠ACD=135°
∴∠MAD=∠NCD,
在△AMD和△CND中,
,
∴△AMD≌△CND(ASA),
∴DM=DN.
22.解:(1)∵DM,EN分别垂直平分AC和BC
∴,
∵△CMN的周长为15cm
∴
∴
∴
AB的长为
(2)由(1)得,
∴,
在中,
∴
根据对顶角的性质可得:,
在中,
在中,
∴
∴
在△ABC中,
∴
∴
23.证明:(1)在△ABO与△CDO中
∵,
∴△ABO≌△CDO(SAS),
∴AB=CD;
(2)如图所示:
延长OF、CE交于点G,
∵∠CEF=140°,∠OFE=110°,
∴∠FEG=40°,∠EFG=70°,
∴∠G=180° 40° 70°=70°,
∴EF=EG,
∵CE=11m,EF=10m,
∴CG=CE+EG=CE+EF=11+10=21m,
∵CG∥AB,
∴∠A=∠C,
在△ABO与△CGO中
,
∴△ABO≌△CGO(ASA)
∴AB=CG=21m.
一、选择题
1.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAC=5∠BAE,则∠C的度数为( )
A.30° B.40° C.50° D.60°
2.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线一点,点E在BC上,且AE=CF,∠CAE=30°,则∠ACF的度数是( )
A.75° B.60° C.55° D.45°
3.如图,在Rt△ABC中,∠ACB=90°.根据尺规作图痕迹,下列结论一定正确的是( )
A.BC=EC B.BE=EC C.BC=BE D.AE=EC
4.如图,在中,,于点 ,点是内一点,连接交于点 ,已知,若点是的内心,则 的度数为( )
A.36° B.48° C.60° D.72°
5.如图,正五边形中,F为边中点,连接,则的度数是( )
A. B. C. D.
6.如图,在中,点O是边和的垂直平分线、的交点,若,则这两条垂直平分线相交所成锐角的度数为( )
A. B. C. D.
7.已知:如图,中,,求证:,在证明该结论时,只添加一条辅助线:①作的平分线交于点,②过点作于点,③取中点,连接,④作的垂直平分线,其中作法正确的个数是( )
A.1 B.2 C.3 D.4
8.如图,在四边形中,点在边上,,,,则的度数为( )
A. B. C. D.
9.如图,为的中线,将沿着翻折得到,点B的对应点为E,与相交于点F,连接,则下列结论一定正确的是( )
A. B. C. D.
10.学习了角平分线及其性质后,某校数学兴趣小组的同学尝试只用一副带刻度的三角板作的角平分线,根据提供的条件,无法判断是角平分线的是( )
A.,P为中点 B.,
C., D.,P为中点
二、填空题
11.如图,在中,,,延长至,使,延长至,使,连接、,则的度数为________.
12.如图,已知△ABC与△ADE均是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=5,AD=AE=4,点D在BC上,连接CE.则△CDE的面积是_________.
13.如图,在中,已知,的垂直平分线与、分别交于点、,如果,那么的度数为___________.
14.在等腰三角形ABC中,AB=AC,AC边上的中垂线交BC边于点D,垂足为E点,∠ABC的平分线交AC边于点F,交DE于点G,连接AD交BF于点H.则下列结论正确的是______.
①C△ABD=AC+BC(C表示周长);
②AH=DH;
③若AB=DB,则∠C=36°;
④若BD=CD,则图中有6个等腰三角形;
⑤若∠BDE=α,则∠BAC=360°﹣2α.
15.如图,四边形ABCD中,E是DC的中点,连接AE,AE平分∠DAB,∠D=∠C=90°,AD=4BC=8,则线段AB的长为__.
三、解答题
16.已知,,,F是CD的中点,求证:.
17.如图,在中,平分,,求证:.
18.如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM.
(1)求证:△AEF是等腰三角形;
(2)求证:DF=DN.
19.如图,在四边形ABCD中,AD // BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且GD=GF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系,并说明理由.
20.如图 ,与为等腰直角三角形,,,,,,连接、.
(1) 如图1 ,求证:△ACD≌△BCE ;
(2) 如图2 ,若、、三点共线,与交于点,且,,求的面积.
21.如图1,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,M、N分别在AB、AC上运动,且满足∠MDN=90°,
(1)试探究DM和DN有何数量关系,并证明.
(2)若M、N分别运动到BA、AC的延长线时,(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由.
22.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若,求的度数.
23.如图1,为测量池塘宽度,可在池塘外的空地上取任意一点,连接、,并分别延长至点,,使,,连接.
(1)求证:;
(2)如图2,受地形条件的影响,于是采取以下措施:延长至点,使,过点作的平行线,延长至点,连接,测得,,,,请直接写出池塘宽度.
【参考答案】
1.B 2.B 3.C 4.B 5.B 6.C 7.B 8.C 9.C 10.D
11.
12.
13.
14.①③⑤
15.10
16.解:如图,连接、,
在和中,
,
.
.
是等腰三角形.
又点是的中点,
,
∴△ACF≌△ADF(SSS),
,
.
17.证明:在上截取,连接,
∵平分
∴
又∵,
∴,
∴,,
可得
∴
∴
18.(1)解:∵∠BAC=90°,AB=AC,AD⊥BC,
∴∠ABC=∠ACB=∠BAD=∠CAD=45°,AD=BD=CD=BC,
∵∠ABC的平分线是BE,
∴∠ABE=∠CBE=∠ABC=22.5°,
∴∠AFE=∠BAD+∠ABE=45°+22.5°=67.5°,
∠AEF=∠ACB+∠CBE=45°+22.5°=67.5°,
∴∠AEF=∠AFE,
∴AF=AE,
∴△AEF是等腰三角形
(2)证明:∵AF=AE,M为EF的中点,∠CAD=45°,
∴∠CAN=∠CAD=22.5°,
∵AD⊥BC,
∴∠BDF=∠ADN=90°,
∵∠AND=∠ACB+∠CAN=45°+22.5°=67.5°,
又∵∠BFD=∠AFE=67.5°,
∴∠BFD=∠AND,
在△BDF和△ADN中
,
∴△BDF≌△ADN(AAS).
∴DF=DN
19.解:(1)如图1,
∵E是AB的中点,
∴AE=BE,
∵AD∥BC,
∴∠A=∠ABF,∠ADE=∠F,
∴△ADE≌△BFE;
(2)如图2,EG⊥DF;
理由是:由(1)得:△ADE≌△BFE,
∴DE=EF,
∵DG=FG,
∴线段EG是等腰三角形DFG的中线,也是高,
∴EG⊥FD;
20.解:(1),都是等腰直角三角形,
,,,
∴
,
在和中,
,
∴△ACD≌△BCE(SAS),
(2)如图2中,过点作于,
,都是等腰直角三角形,
,,,
,
∴△ACD≌△BCE(SAS),
,,
,
,
,
在和中,
,
∴△CQF≌△BEF(AAS),
,,
,
,
.
21.解:(1)DM=DN,
理由:连接AD,
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵D为BC中点,
∴,,∠ADC=90°,
∴∠C=∠BAD,
∵∠ADM+∠AND=∠MDN=90°,∠ADN+∠CDN=90°,
∴∠ADM=∠CDN,
在△AMD和△CND中,
,
∴△AMD≌△CND(ASA),
∴DM=DN;
(2)DM=DN仍然成立,
理由:连接AD,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵D为BC中点,
∴,,∠ADC=90°,
∴∠ACB=∠BAD=∠CAD=45°,
∵∠ADM+∠MDC=90°,∠MDC+∠CDN=90°,
∴∠ADM=∠CDN,
∵∠MAD=MAC+DAC=135°,∠NCD=180°﹣∠ACD=135°
∴∠MAD=∠NCD,
在△AMD和△CND中,
,
∴△AMD≌△CND(ASA),
∴DM=DN.
22.解:(1)∵DM,EN分别垂直平分AC和BC
∴,
∵△CMN的周长为15cm
∴
∴
∴
AB的长为
(2)由(1)得,
∴,
在中,
∴
根据对顶角的性质可得:,
在中,
在中,
∴
∴
在△ABC中,
∴
∴
23.证明:(1)在△ABO与△CDO中
∵,
∴△ABO≌△CDO(SAS),
∴AB=CD;
(2)如图所示:
延长OF、CE交于点G,
∵∠CEF=140°,∠OFE=110°,
∴∠FEG=40°,∠EFG=70°,
∴∠G=180° 40° 70°=70°,
∴EF=EG,
∵CE=11m,EF=10m,
∴CG=CE+EG=CE+EF=11+10=21m,
∵CG∥AB,
∴∠A=∠C,
在△ABO与△CGO中
,
∴△ABO≌△CGO(ASA)
∴AB=CG=21m.
