河北省衡水市桃城区第十四中学2021-2022学年高二上学期二调考试(西校区)数学试卷(Word版含答案)
文档属性
| 名称 | 河北省衡水市桃城区第十四中学2021-2022学年高二上学期二调考试(西校区)数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 12:42:43 | ||
图片预览



文档简介
桃城区第十四中学2021~2022学年度第一学期高二年级二调考试
数 学 试 卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置.
2.回答选择题时,选出每小题答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案书写在答题卡上,写在本试卷上无效.
3.考试结束后,将答题卡交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知数列-1,,-,…,(-1)n .,…,则它的第6项的值为( )
A. B. C. D.
2.已知直线与垂直,则( )
A.或2 B. C. D.0
3.若椭圆与双曲线的焦点相同,则的值为( )
A. B.4 C.6 D.9
4.已知,,,若,,共面,则λ等于( )
A. B. C.3 D.9
5.中心在坐标原点,离心率为的双曲线的焦点在轴上且虚轴长为12,则该双曲线的方程为( )
A. B. C. D.
6.如图,在平行四边形中,,,,沿对角线将折起到的位置,使得平面平面,过的平面与交于,则面积的最小值为( )
A. B. C. D.
7.已知圆的圆心与点关于直线对称,直线与圆相交于、两点,且,则圆的方程为( ).
A. B.
C. D.
8.已知椭圆为C的左 右焦点,为C上一点,且的内心,若的面积为2b,则椭圆的离心率为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.在以下命题中,不正确的命题有( )
A.是共线的充要条件
B.若,则存在唯一的实数,使
C.对空间任意一点和不共线的三点A,B,C,若,则P,A,B,C四点共面
D.若为空间的一个基底,则构成空间的另一个基底
10.已知,,成等差数列,则下列说法中正确的是( )
A.,,可能成等差数列
B.,,一定成等差数列
C.,,(为常数)一定成等差数列
D.,,可能成等差数列
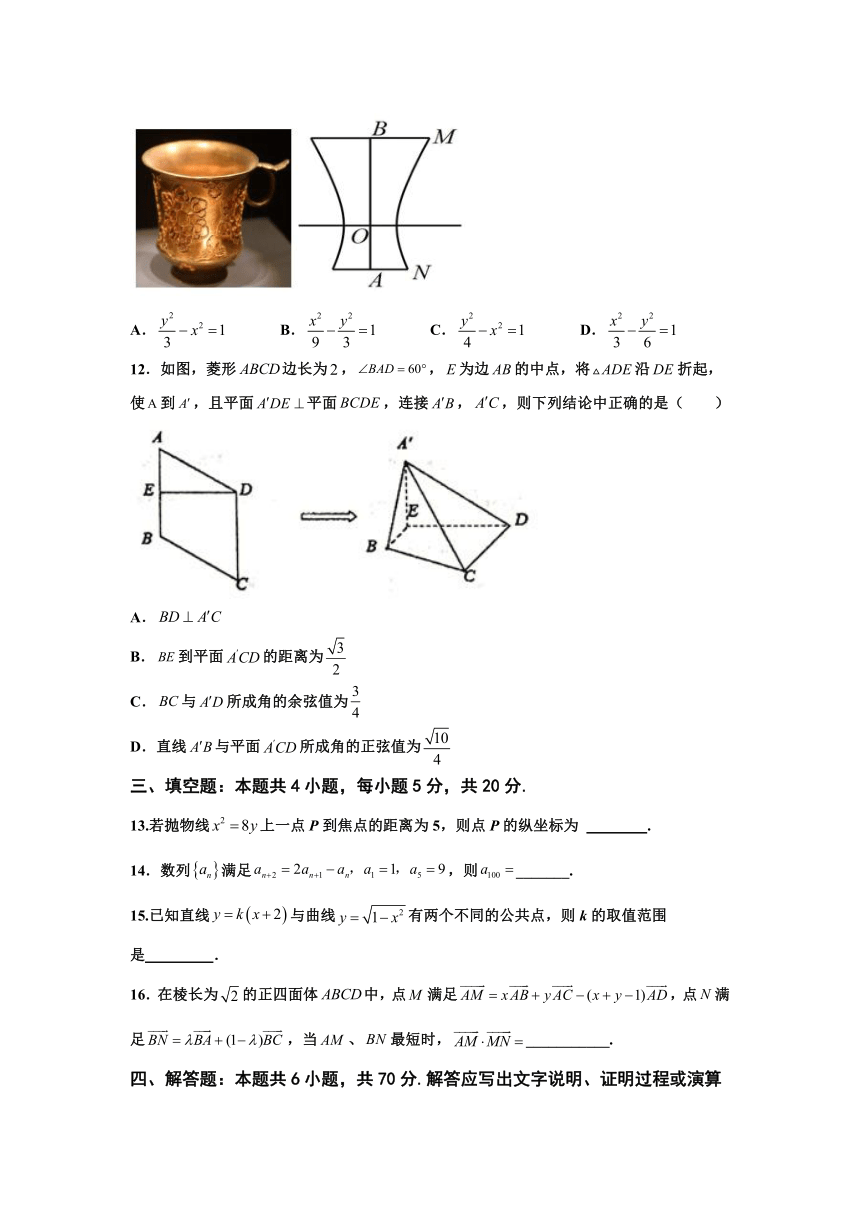
11.如图为陕西博物馆收藏的国宝——唐金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇羡,巧夺天工,是唐代金银细作的典范之作.该杯的主体部分可以近似看作是双曲线的右支与直线围成的曲边四边形绕y旋转一周得到的几何体,若该金杯主体部分的上口外直径为,下底外直径为,则下列曲线中与双曲线C不是共渐近线的有( )
A. B. C. D.
12.如图,菱形边长为,,为边的中点,将沿折起,使到,且平面平面,连接,,则下列结论中正确的是( )
A.
B.到平面的距离为
C.与所成角的余弦值为
D.直线与平面所成角的正弦值为
三、填空题:本题共4小题,每小题5分,共20分.
13.若抛物线上一点P到焦点的距离为5,则点P的纵坐标为 .
14.数列满足,则_______.
15.已知直线与曲线有两个不同的公共点,则k的取值范围是 .
16.在棱长为的正四面体中,点满足,点满足,当、最短时,___________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)在数列{an}中,,通项公式an是n的一次函数.
(1)求{an}的通项公式;
(2)判断96是不是数列{an}中的项?
18.(本小题满分12分)在平面直角坐标系内,已知的三个顶点坐标分别为,.
(1)求边的垂直平分线所在的直线的方程;
(2)若的面积为5,求点的坐标.
19.(本小题满分12分)如图,四棱柱的侧棱平面ABCD,四边形ABCD为菱形,E,F分别为,的中点.,.
(1)证明:B,E,,F四点共面;
(2)求直线AE与平面所成角的正弦值.
20.(本小题满分12分)已知抛物线:,过点的直线交抛物线于,,且(为坐标原点).
(1)求抛物线的方程;
(2)求三角形面积的最小值.
21.(本小题满分12分)如图,在四棱锥中,,,E为棱PA的中点,平面PCD.
(1)求AD的长;
(2)若,平面平面PBC,求二面角的大小的取值范围.
22.(本小题满分12分)已知动圆与圆和圆都外切.
(1)证明动圆圆心M的轨迹C是双曲线的一支,并求其方程;
(2)若直线AB与轨迹C交于A,B两点.,记直线AQ和BQ的斜率分别为,,且,于点P.证明:存在点N,使得为定值.
2021~2022学年度第一学期高二年级二调考试
数 学 参考答案
1.【答案】 D
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】 C
8.【答案】A
9.【答案】AB
10.【答案】ACD
11.【答案】BCD
12.【答案】BC
13.【答案】3
14.【答案】.
15.【答案】
16.【答案】
17.【解】(1)设an=kn+b,k≠0.
则解得∴an=4n-2,n∈N*.
(2)令an=88,即4n-2=96,解得n=24.5 N*.∴96不是数列{an}中的项.
18.【解】(1),,的中点的坐标为, 又设边的垂直平分线所在的直线的斜率为则,
可得的方程为,即.
边的垂直平分线所在的直线的方程
(2)边所在的直线方程为
设边上的高为即点到直线的距离为
且解得 解得或,
点的坐标为或.
19.【解】(1)证明:连接BE,BF,,,取中点,连接、,
因为分别为、中点,易得,,,且,
四边形为平行四边形,,又是中点,,,则四边形为平行四边形,, 因为,,,所以,所以,所以四边形为平行四边形,所以B,E,,F四点共面.
(2)取AB的中点M,连接DM,且,为等边三角形,所以,,
以D为原点,DM,,所在直线分别为x,y,z轴,
由,则,,,,
所以,,,
设平面的法向量为,则,即,令,则,,
设直线AE与平面所成角为,
则,
故直线AE与平面所成角的正弦值为.
20.【解】(1)设直线为代入整理得,设,所以 又所以,由得
综上:所求抛物线的方程为
(2)由(1)得
点到直线的距离为,则
当时,等号成立,
故当时,三角形面积有最小值
21.【解】(1)如图所示:
过E作,交PD于点M,连接,因为平面PCD.平面BCME,平面PCD平面BCME=MC,所以,又因为,所以,所以四边形BCME是平行四边形,所以,又因为,所以.
(2)因为,E为棱PA的中点,所以,且 ,所以,又因为平面平面PBC,平面平面PBC=BP,所以平面PBC,又因为平面PBC,所以,则以点B为原点,分别以BA,BC所在直线为x,y轴,以经过点B且垂直与平面ABCD的直线为z轴建立空间直角坐标系,如图所示:
则,由题意设,则,设平面CDP的一个法向量为,
则,即,令,得,则,易知平面BCP的一个法向量为,
则,
因为,所以,易知二面角的大小为钝角,所以二面角的大小的取值范围是.
22.【解】(1)设动圆圆心,则由题意知:且,
∴,则,
两边平方并整理得:,
两边平方并整理得:,即,.
∴动圆圆心M的轨迹C是双曲线的一支,且方程为,.
(2)若令直线为且,,
联立直线与曲线得:,
,则
由,即,
∴,可得.
∴为,过定点,又于点P,故在以为直径的圆上,
∴存在使,为定值.
数 学 试 卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置.
2.回答选择题时,选出每小题答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案书写在答题卡上,写在本试卷上无效.
3.考试结束后,将答题卡交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知数列-1,,-,…,(-1)n .,…,则它的第6项的值为( )
A. B. C. D.
2.已知直线与垂直,则( )
A.或2 B. C. D.0
3.若椭圆与双曲线的焦点相同,则的值为( )
A. B.4 C.6 D.9
4.已知,,,若,,共面,则λ等于( )
A. B. C.3 D.9
5.中心在坐标原点,离心率为的双曲线的焦点在轴上且虚轴长为12,则该双曲线的方程为( )
A. B. C. D.
6.如图,在平行四边形中,,,,沿对角线将折起到的位置,使得平面平面,过的平面与交于,则面积的最小值为( )
A. B. C. D.
7.已知圆的圆心与点关于直线对称,直线与圆相交于、两点,且,则圆的方程为( ).
A. B.
C. D.
8.已知椭圆为C的左 右焦点,为C上一点,且的内心,若的面积为2b,则椭圆的离心率为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.在以下命题中,不正确的命题有( )
A.是共线的充要条件
B.若,则存在唯一的实数,使
C.对空间任意一点和不共线的三点A,B,C,若,则P,A,B,C四点共面
D.若为空间的一个基底,则构成空间的另一个基底
10.已知,,成等差数列,则下列说法中正确的是( )
A.,,可能成等差数列
B.,,一定成等差数列
C.,,(为常数)一定成等差数列
D.,,可能成等差数列
11.如图为陕西博物馆收藏的国宝——唐金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇羡,巧夺天工,是唐代金银细作的典范之作.该杯的主体部分可以近似看作是双曲线的右支与直线围成的曲边四边形绕y旋转一周得到的几何体,若该金杯主体部分的上口外直径为,下底外直径为,则下列曲线中与双曲线C不是共渐近线的有( )
A. B. C. D.
12.如图,菱形边长为,,为边的中点,将沿折起,使到,且平面平面,连接,,则下列结论中正确的是( )
A.
B.到平面的距离为
C.与所成角的余弦值为
D.直线与平面所成角的正弦值为
三、填空题:本题共4小题,每小题5分,共20分.
13.若抛物线上一点P到焦点的距离为5,则点P的纵坐标为 .
14.数列满足,则_______.
15.已知直线与曲线有两个不同的公共点,则k的取值范围是 .
16.在棱长为的正四面体中,点满足,点满足,当、最短时,___________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)在数列{an}中,,通项公式an是n的一次函数.
(1)求{an}的通项公式;
(2)判断96是不是数列{an}中的项?
18.(本小题满分12分)在平面直角坐标系内,已知的三个顶点坐标分别为,.
(1)求边的垂直平分线所在的直线的方程;
(2)若的面积为5,求点的坐标.
19.(本小题满分12分)如图,四棱柱的侧棱平面ABCD,四边形ABCD为菱形,E,F分别为,的中点.,.
(1)证明:B,E,,F四点共面;
(2)求直线AE与平面所成角的正弦值.
20.(本小题满分12分)已知抛物线:,过点的直线交抛物线于,,且(为坐标原点).
(1)求抛物线的方程;
(2)求三角形面积的最小值.
21.(本小题满分12分)如图,在四棱锥中,,,E为棱PA的中点,平面PCD.
(1)求AD的长;
(2)若,平面平面PBC,求二面角的大小的取值范围.
22.(本小题满分12分)已知动圆与圆和圆都外切.
(1)证明动圆圆心M的轨迹C是双曲线的一支,并求其方程;
(2)若直线AB与轨迹C交于A,B两点.,记直线AQ和BQ的斜率分别为,,且,于点P.证明:存在点N,使得为定值.
2021~2022学年度第一学期高二年级二调考试
数 学 参考答案
1.【答案】 D
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】 C
8.【答案】A
9.【答案】AB
10.【答案】ACD
11.【答案】BCD
12.【答案】BC
13.【答案】3
14.【答案】.
15.【答案】
16.【答案】
17.【解】(1)设an=kn+b,k≠0.
则解得∴an=4n-2,n∈N*.
(2)令an=88,即4n-2=96,解得n=24.5 N*.∴96不是数列{an}中的项.
18.【解】(1),,的中点的坐标为, 又设边的垂直平分线所在的直线的斜率为则,
可得的方程为,即.
边的垂直平分线所在的直线的方程
(2)边所在的直线方程为
设边上的高为即点到直线的距离为
且解得 解得或,
点的坐标为或.
19.【解】(1)证明:连接BE,BF,,,取中点,连接、,
因为分别为、中点,易得,,,且,
四边形为平行四边形,,又是中点,,,则四边形为平行四边形,, 因为,,,所以,所以,所以四边形为平行四边形,所以B,E,,F四点共面.
(2)取AB的中点M,连接DM,且,为等边三角形,所以,,
以D为原点,DM,,所在直线分别为x,y,z轴,
由,则,,,,
所以,,,
设平面的法向量为,则,即,令,则,,
设直线AE与平面所成角为,
则,
故直线AE与平面所成角的正弦值为.
20.【解】(1)设直线为代入整理得,设,所以 又所以,由得
综上:所求抛物线的方程为
(2)由(1)得
点到直线的距离为,则
当时,等号成立,
故当时,三角形面积有最小值
21.【解】(1)如图所示:
过E作,交PD于点M,连接,因为平面PCD.平面BCME,平面PCD平面BCME=MC,所以,又因为,所以,所以四边形BCME是平行四边形,所以,又因为,所以.
(2)因为,E为棱PA的中点,所以,且 ,所以,又因为平面平面PBC,平面平面PBC=BP,所以平面PBC,又因为平面PBC,所以,则以点B为原点,分别以BA,BC所在直线为x,y轴,以经过点B且垂直与平面ABCD的直线为z轴建立空间直角坐标系,如图所示:
则,由题意设,则,设平面CDP的一个法向量为,
则,即,令,得,则,易知平面BCP的一个法向量为,
则,
因为,所以,易知二面角的大小为钝角,所以二面角的大小的取值范围是.
22.【解】(1)设动圆圆心,则由题意知:且,
∴,则,
两边平方并整理得:,
两边平方并整理得:,即,.
∴动圆圆心M的轨迹C是双曲线的一支,且方程为,.
(2)若令直线为且,,
联立直线与曲线得:,
,则
由,即,
∴,可得.
∴为,过定点,又于点P,故在以为直径的圆上,
∴存在使,为定值.
同课章节目录
