4.1指数课件-2021-2022学年高一数学人教A版(2019)必修一(共36张PPT)
文档属性
| 名称 | 4.1指数课件-2021-2022学年高一数学人教A版(2019)必修一(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 357.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 13:03:38 | ||
图片预览







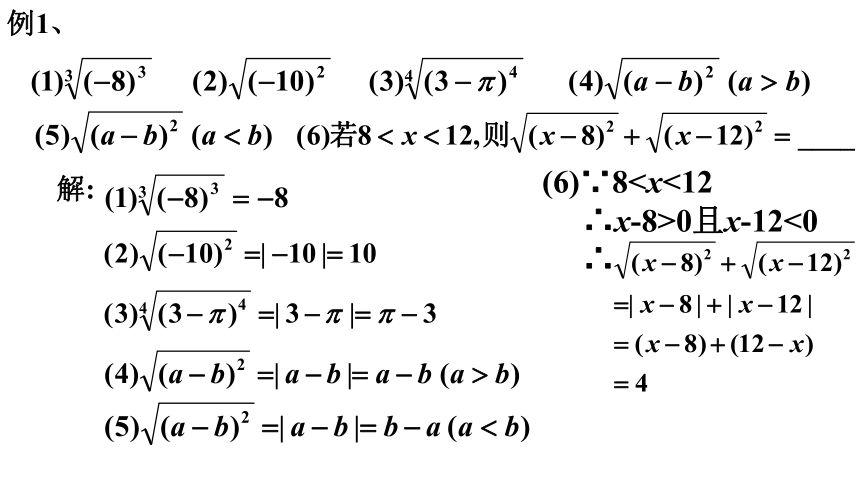


文档简介
(共36张PPT)
4.1.1 n次方根与分数指数幂
一、知识回顾
在初中,我们研究了正整数指数幂:一个数a的n次幂等于n个a连乘的积,即
an=a·a· ··· ·a
n个
正整数指数幂的运算法则有五条:
1.am·an=am+n;
2.am÷an=am-n;
3.(am)n=amn;
4.(ab)n=an·bn;
5.
另外,我们规定:
m,n∈N+
m,n∈R
二、探索新知
类似地,(±2)4=16 ±2叫做16的4次方根.
25=32 2叫做32的5次方根.
……
xn=a x就是a的n次方根.
根式
一般地,如xn=a,那么x叫做a的n次方根,其中n>1,且n∈ N* .
我们知道,如果x2=a,那么x叫做a的平方根.
如果x3=a,那么x叫做a的立方根.
若x3=-27,则x=__________
若x5=32,则x=__________
若x7=-128,则x=__________
……
若x2=9,则x=___________
若x4=16,则x=___________
若x6=64,则x=___________
……
二、探索新知
规律
当n是奇数时,正数的n次方根是一个正数
负数的n次方根是一个负数
当n是偶数时,正数的n次方根有两个,互为相反数
负数没有偶次方根
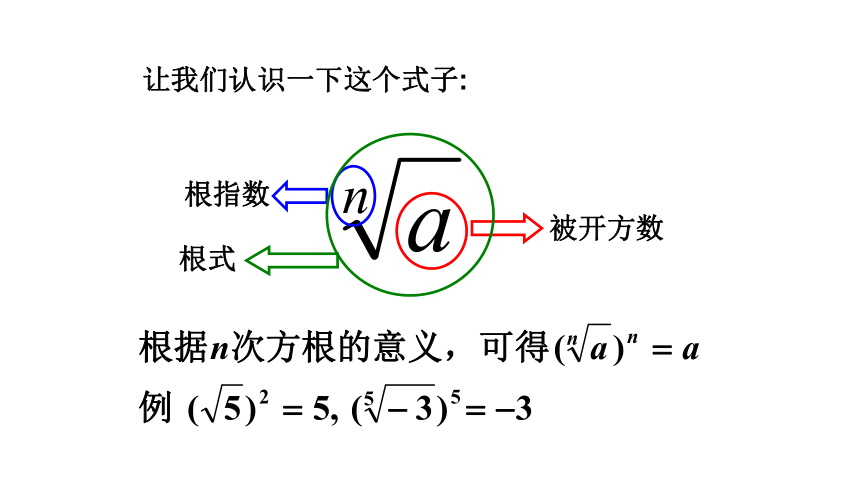
根指数
被开方数
根式
让我们认识一下这个式子:
表示an的n次方根,等式 一定成立吗 如果不一定成立,那么 等于什么
三、探究
=-2
=2
=2
=2
例1、
解:
(6)∵8∴x-8>0且x-12<0
∴
练习
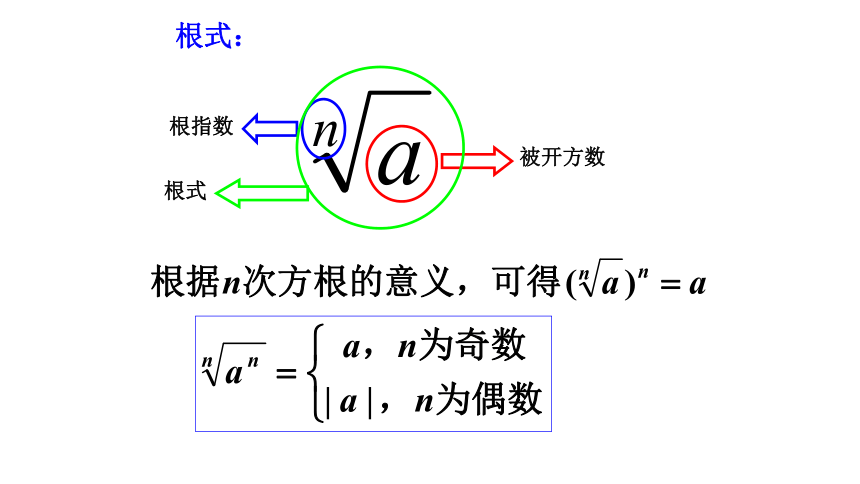
n次方根:
如果xn=a,那么x叫做a的n次方根(其中n>1,且n∈N*)
0的任何次方根都是0,记作
负数没有偶次方根.
四、小结:
根指数
被开方数
根式
根式:
(1)观察以下式子,并总结出规律:(a > 0)
结论:当根式的被开方数的指数能被根指数整除时,根式可以表示为分数指数幂的形式.
合作探究
根式与分数指数幂的互化
(2)利用(1)的规律,你能表示下列式子吗
总结:当根式的被开方数的指数不能被根指数整除时,根式可以写成分数指数幂的形式.
(3)你能用方根的意义解释(2)的式子吗
43的5次方根是
75的3次方根是
a2的3次方根是
a9的7次方根是
结果表明:方根的结果与分数指数幂是相通的.
综上,我们得到正数的正分数指数幂的意义.
1.正数的正分数指数幂的意义:
注意:
1、分数指数幂是根式的另一种新的写法,可以互换,只是形式上的不同,不可将其理解为 个a相乘;
2、公式成立的前提条件:a>0;
我们规定:
2、正数的负分数指数幂的意义是
3、0的正分数指数幂等于0,
0的负分数指数幂没有意义.
说明:
(1)分数指数幂的意义只是一种规定,前面所举的例子只表示这种规定的合理性;
(2)规定了分数指数幂的意义以后,指数的概念就从整数指数推广到了有理数指数;
(3)关于整数指数幂的运算性质,对于有理指数幂也同样适用,即对任意有理数r,s,均有下面的性质:
(a>0,r,s∈Q);
(a>0,r,s∈Q);
(a>0,b>0,r∈Q);
课本P107页练习1
练习:用根式的形式表示下列各式
例题讲解
例2、求值:
例3、用分数指数幂的形式表示下列各式:
当有多重根式时,要由里向外层层转化
对于有分母的,可以先把分母写成负指数幂.
练习:课本P107页第2题
例4、计算下列各式(式中的字母都是正数)
例5、计算下列各式
练习 P107页练习题第3题
无理指数幂
探究:
在前面的学习中,我们已经把指数由正整数推广到了有理数,那么,能不能继续推广到实数范围呢?
(1)一般地,无理数指数幂aa(a>0,a是无理数)是一个确定的实数;
(2)有理数指数幂的运算性质同样适用于无理数指数幂,即:
①aa·ab=aa+b(a>0,a,b是无理数);
②(aa)b=aab(a>0,a,b是无理数);
③(ab)a=aaba(a>0,b>0,a是无理数).
求值
2.求值.
(1) 7
(2) 47
(3) 8
1、n次方根和根式的概念。
2、当n为奇数时,a的n次方根是 。
当n为偶数时,正数a的n次方根是
负数没有偶次方根。
3、0的任何次方根都是0
当n是奇数时,
当n是偶数时,
课堂小结
4、分数指数概念
5、有理指数幂运算性质
(3)0的正分数指数幂为0,0的负分数指数幂没有意义.
课堂练习
1、判断:下列正确的是( )
C
2、计算下列各式
作业
A本 P109页习题4.1第4、5题
4.1.1 n次方根与分数指数幂
一、知识回顾
在初中,我们研究了正整数指数幂:一个数a的n次幂等于n个a连乘的积,即
an=a·a· ··· ·a
n个
正整数指数幂的运算法则有五条:
1.am·an=am+n;
2.am÷an=am-n;
3.(am)n=amn;
4.(ab)n=an·bn;
5.
另外,我们规定:
m,n∈N+
m,n∈R
二、探索新知
类似地,(±2)4=16 ±2叫做16的4次方根.
25=32 2叫做32的5次方根.
……
xn=a x就是a的n次方根.
根式
一般地,如xn=a,那么x叫做a的n次方根,其中n>1,且n∈ N* .
我们知道,如果x2=a,那么x叫做a的平方根.
如果x3=a,那么x叫做a的立方根.
若x3=-27,则x=__________
若x5=32,则x=__________
若x7=-128,则x=__________
……
若x2=9,则x=___________
若x4=16,则x=___________
若x6=64,则x=___________
……
二、探索新知
规律
当n是奇数时,正数的n次方根是一个正数
负数的n次方根是一个负数
当n是偶数时,正数的n次方根有两个,互为相反数
负数没有偶次方根
根指数
被开方数
根式
让我们认识一下这个式子:
表示an的n次方根,等式 一定成立吗 如果不一定成立,那么 等于什么
三、探究
=-2
=2
=2
=2
例1、
解:
(6)∵8
∴
练习
n次方根:
如果xn=a,那么x叫做a的n次方根(其中n>1,且n∈N*)
0的任何次方根都是0,记作
负数没有偶次方根.
四、小结:
根指数
被开方数
根式
根式:
(1)观察以下式子,并总结出规律:(a > 0)
结论:当根式的被开方数的指数能被根指数整除时,根式可以表示为分数指数幂的形式.
合作探究
根式与分数指数幂的互化
(2)利用(1)的规律,你能表示下列式子吗
总结:当根式的被开方数的指数不能被根指数整除时,根式可以写成分数指数幂的形式.
(3)你能用方根的意义解释(2)的式子吗
43的5次方根是
75的3次方根是
a2的3次方根是
a9的7次方根是
结果表明:方根的结果与分数指数幂是相通的.
综上,我们得到正数的正分数指数幂的意义.
1.正数的正分数指数幂的意义:
注意:
1、分数指数幂是根式的另一种新的写法,可以互换,只是形式上的不同,不可将其理解为 个a相乘;
2、公式成立的前提条件:a>0;
我们规定:
2、正数的负分数指数幂的意义是
3、0的正分数指数幂等于0,
0的负分数指数幂没有意义.
说明:
(1)分数指数幂的意义只是一种规定,前面所举的例子只表示这种规定的合理性;
(2)规定了分数指数幂的意义以后,指数的概念就从整数指数推广到了有理数指数;
(3)关于整数指数幂的运算性质,对于有理指数幂也同样适用,即对任意有理数r,s,均有下面的性质:
(a>0,r,s∈Q);
(a>0,r,s∈Q);
(a>0,b>0,r∈Q);
课本P107页练习1
练习:用根式的形式表示下列各式
例题讲解
例2、求值:
例3、用分数指数幂的形式表示下列各式:
当有多重根式时,要由里向外层层转化
对于有分母的,可以先把分母写成负指数幂.
练习:课本P107页第2题
例4、计算下列各式(式中的字母都是正数)
例5、计算下列各式
练习 P107页练习题第3题
无理指数幂
探究:
在前面的学习中,我们已经把指数由正整数推广到了有理数,那么,能不能继续推广到实数范围呢?
(1)一般地,无理数指数幂aa(a>0,a是无理数)是一个确定的实数;
(2)有理数指数幂的运算性质同样适用于无理数指数幂,即:
①aa·ab=aa+b(a>0,a,b是无理数);
②(aa)b=aab(a>0,a,b是无理数);
③(ab)a=aaba(a>0,b>0,a是无理数).
求值
2.求值.
(1) 7
(2) 47
(3) 8
1、n次方根和根式的概念。
2、当n为奇数时,a的n次方根是 。
当n为偶数时,正数a的n次方根是
负数没有偶次方根。
3、0的任何次方根都是0
当n是奇数时,
当n是偶数时,
课堂小结
4、分数指数概念
5、有理指数幂运算性质
(3)0的正分数指数幂为0,0的负分数指数幂没有意义.
课堂练习
1、判断:下列正确的是( )
C
2、计算下列各式
作业
A本 P109页习题4.1第4、5题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
