2021--2022学年人教版 九年级上册数学23.2中心对称尖子生培优练 (word解析版)
文档属性
| 名称 | 2021--2022学年人教版 九年级上册数学23.2中心对称尖子生培优练 (word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 341.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 00:00:00 | ||
图片预览



文档简介
23.2中心对称尖子生培优练---2021--2022学年人教版(2012)九年级上学期第二十三章旋转
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
2.等腰三角形、等边三角形、矩形、正方形和圆这五种图形中,既是轴对称图形又是中心对称图形的图形种数是( ).
A.2 B.3 C.4 D.5
3.如图,已知长方形的长为10,宽为4,则图中阴影部分的面积为( )
A.20 B.15 C.10 D.25
4.在平面直角坐标系xOy中,点A(﹣2,3)关于点O中心对称的点的坐标是( )
A.(2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(﹣2,3)
5.下列四个图形中,可以看作是中心对称图的是( )
A. B.
C. D.
6.点(3,5)与点(﹣3,﹣5)的位置关系是( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.关于第二、四象限的角平分线对称
7.点A(﹣3,a)与点B(3,4)关于原点对称,则a的值为( )
A.﹣3 B.﹣4 C.3 D.4
8.如图,点O是 ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABFE和四边形EFCD的面积分别记为S1,S2,那么S1,S2之间的关系为( )
A.S1>S2 B.S1<S2 C.S1=S2 D.无法确定
评卷人得分
二、填空题
9.点P(2,﹣3)与点P′关于原点成中心对称,则P′的坐标为 ___.
10.在平面直角坐标系中,点与点关于原点对称,则________.
11.给出以下4个图形:①等边三角形,②平行四边形,③菱形,④正方形.其中既是轴对称图形又是中心对称图形的是 _____.(填写序号)
12.如图,直线EF经过平行四边形ABCD的对角线的交点,若AE=3 cm,四边形AEFB的面积为15 cm2,则CF=____,四边形EDCF的面积为____.
13.如图,已知矩形OACB的两边OA,OB分别在x轴、y轴上,且A(﹣1,0),B(0,2),先将矩形OACB沿x轴向右平移2个单位长度,得到矩形O1A1C1B1,然后作矩形O1A1C1B1关于坐标原点O的中心对称图形,得到矩形O2A2C2B2,则点C2的坐标是_____.
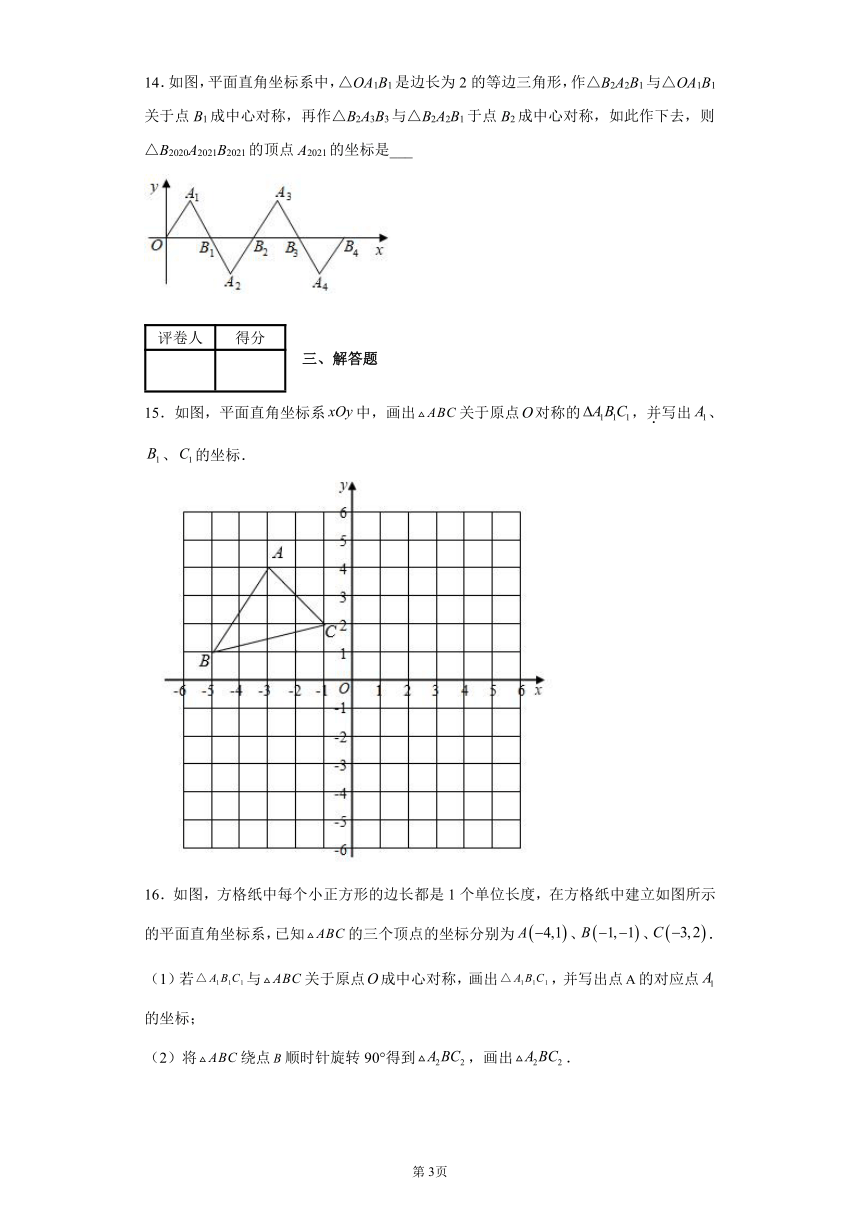
14.如图,平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1于点B2成中心对称,如此作下去,则△B2020A2021B2021的顶点A2021的坐标是___
评卷人得分
三、解答题
15.如图,平面直角坐标系中,画出关于原点对称的,并写出、、的坐标.
16.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,已知的三个顶点的坐标分别为、、.
(1)若与关于原点成中心对称,画出,并写出点的对应点的坐标;
(2)将绕点顺时针旋转90°得到,画出.
17.如图,,分别是两个半圆的圆心,这个图形是中心对称图形吗?如果不是,请说明理由;如果是,请指出对称中心.
18.如图,已知点的坐标为,点的坐标为,菱形的对角线交于坐标原点.求,两点的坐标.
19.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(2,﹣2),B(0,﹣5),C(0,﹣2).
(1)画△A1B1C1,使它与△ABC关于点C成中心对称,则A1的坐标为 .
(2)平移△ABC,使点B的对应点B2的坐标为(2,3),画出平移后对应的△A2B2C2,则A2的坐标为 .
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为 .
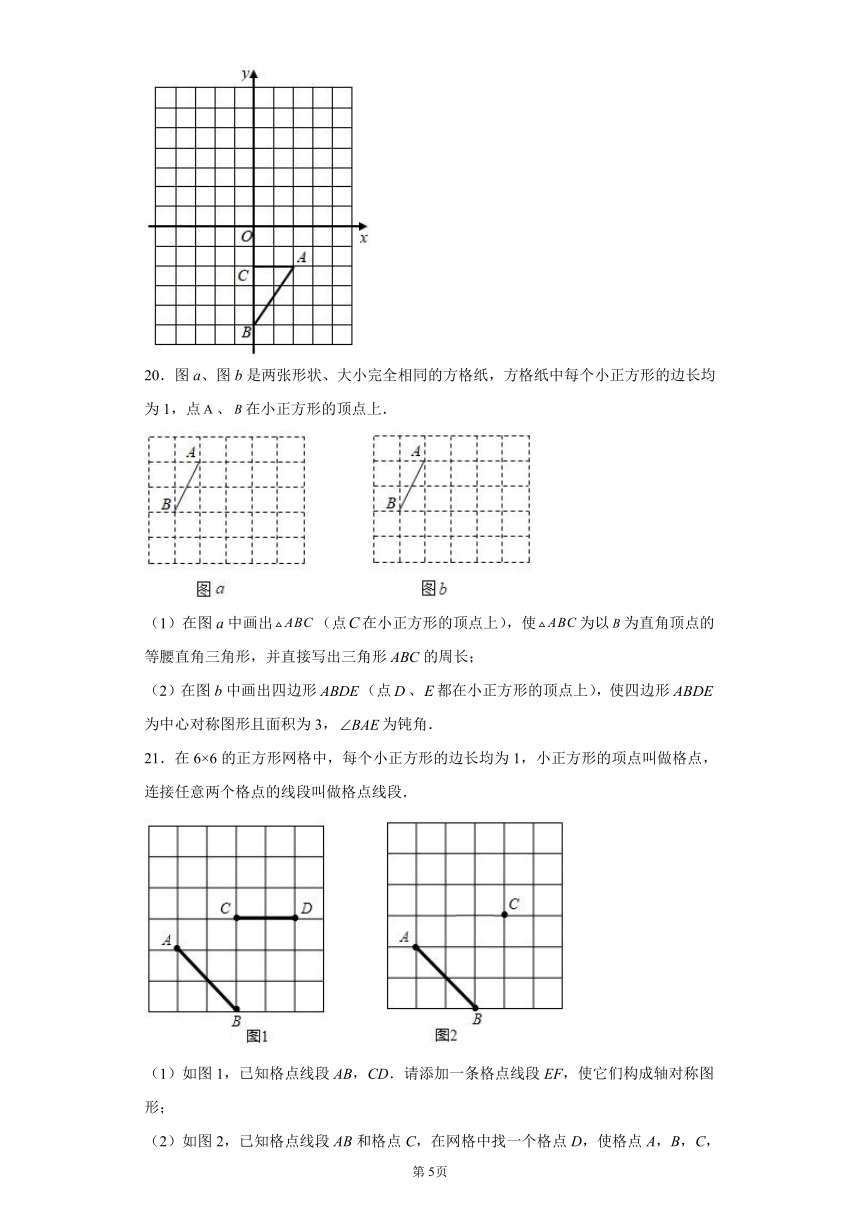
20.图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点、在小正方形的顶点上.
(1)在图a中画出(点在小正方形的顶点上),使为以为直角顶点的等腰直角三角形,并直接写出三角形ABC的周长;
(2)在图b中画出四边形(点、都在小正方形的顶点上),使四边形为中心对称图形且面积为3,为钝角.
21.在6×6的正方形网格中,每个小正方形的边长均为1,小正方形的项点叫做格点,连接任意两个格点的线段叫做格点线段.
(1)如图1,已知格点线段AB,CD.请添加一条格点线段EF,使它们构成轴对称图形;
(2)如图2,已知格点线段AB和格点C,在网格中找一个格点D,使格点A,B,C,D四点构成中心对称图形,并直接写出你所画的四边形的面积.(画出一种即可)
试卷第1页,共3页
第1页
参考答案
1.D
【详解】
A.等边三角形是轴对称图形,不是中心对称图形,故本选项不合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.平行四边形是中心对称图形,不是轴对称图形,故本选项不合题意;
D.矩形既是中心对称图形又是轴对称图形,故本选项符合题意.
故选:D.
2.B
解:等腰三角形、等边三角形是轴对称图形,不是中心对称图形,不符合题意;
矩形、正方形和圆是轴对称图形,也是中心对称图形,符合题意.
故既是轴对称图形又是中心对称图形的是矩形、正方形和圆共3个.
故选:B.
3.A
解:根据题意观察图形可知,长方形的面积=10×4=40cm2,
再根据中心对称的性质得:
图中阴影部分的面积即是长方形面积的一半,
则图中阴影部分的面积=×40=20cm2.
故选:A.
4.C
解:∵点A(﹣2,3)与点B关于原点O中心对称,
∴点B的坐标为:(2,﹣3).
故选:C.
5.C
解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
6.C
【详解】
∵点(3,5)与点(﹣3,﹣5)横纵坐标都互为相反数,
∴点(3,5)与点(﹣3,﹣5)关于原点对称.
故选:C.
7.B
【详解】
∵点A(﹣3,a)与点B(3,4)关于原点对称,
∴a=﹣4.
故选:B.
8.C
【详解】
点O是 ABCD的对称中心
OB=OD,AD∥BC
∠ADB=∠CBD
在△BOF和△DOE中
△BOF△DOE
S△BOF=S△DOE
BD是 ABCD的对角线
故选:C.
9.(-2,3)
解:点P(2,-3)与点P′关于原点对称,则点P′的坐标(-2,3).
故答案为:(-2,3).
10.8
解:∵点A(a,3)与点B(-5,b)关于原点对称,
∴a=5,b=-3,
∴a-b=-5-(-3)=8,
故答案为:8.
11.③④
解:等边三角形是轴对称图形,但不是中心对称图形,①不符合;
平行四边形是中心对称图形,但不是轴对称图形,②不符合;
菱形是中心对称图形,也是轴对称图形,③符合;
正方形是中心对称图形,也是轴对称图形,④符合;
故答案为③④
12.3 15
解:连接AC,BD,
∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,
∴∠EAO=∠FCO.
在△AOE与△COF中,∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF=3cm.
同理可得△AOB≌△COD,△BOF≌△DOE,
∴S四边形EDCF=S四边形AEFB=15cm2.
故答案为3cm,15cm2.
13.(﹣1,﹣2).
解:由题意得C(-1,2),则沿x轴向右平移2个单位长度后得到的C1点坐标为(1,2),则C1点关于原点的对称点C2的坐标为(-1,-2),
故答案为:(-1,-2).
14.
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵,,
∴点A2的坐标是,
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵,,
∴点A3的坐标是,
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵,
∴点A4的坐标是,
……,
∴An的横坐标是:2n-1,
当n为奇数时,An的纵坐标是,当n为偶数时,An的纵坐标是,
∴顶点A2021的坐标是,
故答案为:.
15.图见解析,,、
解:∵A(-3,4),B(-5,1),C(-1,2)
∴它们关于原点对称的点分别为,、 ,
画图如下:为所求作的图形.
16.(1)图见解析,点的坐标为;(2)见解析
解:(1)如图所示,即为所求,点的坐标为.
(2)如图所示,即为所求.
17.是中心对称图形,对称中心是线段的中点.
解:这个图形是中心对称图形,对称中心是线段的中点.
如图所示,补齐两个圆,连接两个圆的交点,与的交点即为所求,并且交点是的中点.
18.C,D
解: 菱形的对角线交于坐标原点.点的坐标为,点的坐标为,
点C和点A关于原点O对称,点D和点B关于原点O对称,
∴ C (2,-2); D(1,).
19.(1)图见解析,(﹣2,﹣2);(2)图见解析,(4,6);(3)(1,2).
解:(1)如图,△A1B1C1即为所求,A1的坐标为(﹣2,﹣2).
故答案为:(﹣2,﹣2).
(2)如图,△A2B2C2即为所求,A2的坐标为(4,6).
故答案为:(4,6).
(3)旋转中心P的坐标为(1,2),
故答案为:(1,2).
20.(1)图见解析,;(2)见解析
解:(1)如图a,即为所求;
由图可知:,,
∴;
(2)如图b,四边形即为所求.
21.解:(1)如图1中,线段EF即为所求作.
(2)如图2中,四边形ABCD即为所求作.
S平行四边形ABCD=3×5-2××1×3-2××2×2=8.
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
2.等腰三角形、等边三角形、矩形、正方形和圆这五种图形中,既是轴对称图形又是中心对称图形的图形种数是( ).
A.2 B.3 C.4 D.5
3.如图,已知长方形的长为10,宽为4,则图中阴影部分的面积为( )
A.20 B.15 C.10 D.25
4.在平面直角坐标系xOy中,点A(﹣2,3)关于点O中心对称的点的坐标是( )
A.(2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(﹣2,3)
5.下列四个图形中,可以看作是中心对称图的是( )
A. B.
C. D.
6.点(3,5)与点(﹣3,﹣5)的位置关系是( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.关于第二、四象限的角平分线对称
7.点A(﹣3,a)与点B(3,4)关于原点对称,则a的值为( )
A.﹣3 B.﹣4 C.3 D.4
8.如图,点O是 ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABFE和四边形EFCD的面积分别记为S1,S2,那么S1,S2之间的关系为( )
A.S1>S2 B.S1<S2 C.S1=S2 D.无法确定
评卷人得分
二、填空题
9.点P(2,﹣3)与点P′关于原点成中心对称,则P′的坐标为 ___.
10.在平面直角坐标系中,点与点关于原点对称,则________.
11.给出以下4个图形:①等边三角形,②平行四边形,③菱形,④正方形.其中既是轴对称图形又是中心对称图形的是 _____.(填写序号)
12.如图,直线EF经过平行四边形ABCD的对角线的交点,若AE=3 cm,四边形AEFB的面积为15 cm2,则CF=____,四边形EDCF的面积为____.
13.如图,已知矩形OACB的两边OA,OB分别在x轴、y轴上,且A(﹣1,0),B(0,2),先将矩形OACB沿x轴向右平移2个单位长度,得到矩形O1A1C1B1,然后作矩形O1A1C1B1关于坐标原点O的中心对称图形,得到矩形O2A2C2B2,则点C2的坐标是_____.
14.如图,平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1于点B2成中心对称,如此作下去,则△B2020A2021B2021的顶点A2021的坐标是___
评卷人得分
三、解答题
15.如图,平面直角坐标系中,画出关于原点对称的,并写出、、的坐标.
16.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,已知的三个顶点的坐标分别为、、.
(1)若与关于原点成中心对称,画出,并写出点的对应点的坐标;
(2)将绕点顺时针旋转90°得到,画出.
17.如图,,分别是两个半圆的圆心,这个图形是中心对称图形吗?如果不是,请说明理由;如果是,请指出对称中心.
18.如图,已知点的坐标为,点的坐标为,菱形的对角线交于坐标原点.求,两点的坐标.
19.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(2,﹣2),B(0,﹣5),C(0,﹣2).
(1)画△A1B1C1,使它与△ABC关于点C成中心对称,则A1的坐标为 .
(2)平移△ABC,使点B的对应点B2的坐标为(2,3),画出平移后对应的△A2B2C2,则A2的坐标为 .
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为 .
20.图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点、在小正方形的顶点上.
(1)在图a中画出(点在小正方形的顶点上),使为以为直角顶点的等腰直角三角形,并直接写出三角形ABC的周长;
(2)在图b中画出四边形(点、都在小正方形的顶点上),使四边形为中心对称图形且面积为3,为钝角.
21.在6×6的正方形网格中,每个小正方形的边长均为1,小正方形的项点叫做格点,连接任意两个格点的线段叫做格点线段.
(1)如图1,已知格点线段AB,CD.请添加一条格点线段EF,使它们构成轴对称图形;
(2)如图2,已知格点线段AB和格点C,在网格中找一个格点D,使格点A,B,C,D四点构成中心对称图形,并直接写出你所画的四边形的面积.(画出一种即可)
试卷第1页,共3页
第1页
参考答案
1.D
【详解】
A.等边三角形是轴对称图形,不是中心对称图形,故本选项不合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.平行四边形是中心对称图形,不是轴对称图形,故本选项不合题意;
D.矩形既是中心对称图形又是轴对称图形,故本选项符合题意.
故选:D.
2.B
解:等腰三角形、等边三角形是轴对称图形,不是中心对称图形,不符合题意;
矩形、正方形和圆是轴对称图形,也是中心对称图形,符合题意.
故既是轴对称图形又是中心对称图形的是矩形、正方形和圆共3个.
故选:B.
3.A
解:根据题意观察图形可知,长方形的面积=10×4=40cm2,
再根据中心对称的性质得:
图中阴影部分的面积即是长方形面积的一半,
则图中阴影部分的面积=×40=20cm2.
故选:A.
4.C
解:∵点A(﹣2,3)与点B关于原点O中心对称,
∴点B的坐标为:(2,﹣3).
故选:C.
5.C
解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
6.C
【详解】
∵点(3,5)与点(﹣3,﹣5)横纵坐标都互为相反数,
∴点(3,5)与点(﹣3,﹣5)关于原点对称.
故选:C.
7.B
【详解】
∵点A(﹣3,a)与点B(3,4)关于原点对称,
∴a=﹣4.
故选:B.
8.C
【详解】
点O是 ABCD的对称中心
OB=OD,AD∥BC
∠ADB=∠CBD
在△BOF和△DOE中
△BOF△DOE
S△BOF=S△DOE
BD是 ABCD的对角线
故选:C.
9.(-2,3)
解:点P(2,-3)与点P′关于原点对称,则点P′的坐标(-2,3).
故答案为:(-2,3).
10.8
解:∵点A(a,3)与点B(-5,b)关于原点对称,
∴a=5,b=-3,
∴a-b=-5-(-3)=8,
故答案为:8.
11.③④
解:等边三角形是轴对称图形,但不是中心对称图形,①不符合;
平行四边形是中心对称图形,但不是轴对称图形,②不符合;
菱形是中心对称图形,也是轴对称图形,③符合;
正方形是中心对称图形,也是轴对称图形,④符合;
故答案为③④
12.3 15
解:连接AC,BD,
∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,
∴∠EAO=∠FCO.
在△AOE与△COF中,∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF=3cm.
同理可得△AOB≌△COD,△BOF≌△DOE,
∴S四边形EDCF=S四边形AEFB=15cm2.
故答案为3cm,15cm2.
13.(﹣1,﹣2).
解:由题意得C(-1,2),则沿x轴向右平移2个单位长度后得到的C1点坐标为(1,2),则C1点关于原点的对称点C2的坐标为(-1,-2),
故答案为:(-1,-2).
14.
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵,,
∴点A2的坐标是,
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵,,
∴点A3的坐标是,
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵,
∴点A4的坐标是,
……,
∴An的横坐标是:2n-1,
当n为奇数时,An的纵坐标是,当n为偶数时,An的纵坐标是,
∴顶点A2021的坐标是,
故答案为:.
15.图见解析,,、
解:∵A(-3,4),B(-5,1),C(-1,2)
∴它们关于原点对称的点分别为,、 ,
画图如下:为所求作的图形.
16.(1)图见解析,点的坐标为;(2)见解析
解:(1)如图所示,即为所求,点的坐标为.
(2)如图所示,即为所求.
17.是中心对称图形,对称中心是线段的中点.
解:这个图形是中心对称图形,对称中心是线段的中点.
如图所示,补齐两个圆,连接两个圆的交点,与的交点即为所求,并且交点是的中点.
18.C,D
解: 菱形的对角线交于坐标原点.点的坐标为,点的坐标为,
点C和点A关于原点O对称,点D和点B关于原点O对称,
∴ C (2,-2); D(1,).
19.(1)图见解析,(﹣2,﹣2);(2)图见解析,(4,6);(3)(1,2).
解:(1)如图,△A1B1C1即为所求,A1的坐标为(﹣2,﹣2).
故答案为:(﹣2,﹣2).
(2)如图,△A2B2C2即为所求,A2的坐标为(4,6).
故答案为:(4,6).
(3)旋转中心P的坐标为(1,2),
故答案为:(1,2).
20.(1)图见解析,;(2)见解析
解:(1)如图a,即为所求;
由图可知:,,
∴;
(2)如图b,四边形即为所求.
21.解:(1)如图1中,线段EF即为所求作.
(2)如图2中,四边形ABCD即为所求作.
S平行四边形ABCD=3×5-2××1×3-2××2×2=8.
同课章节目录
