2021-2022七上 5.2平面直角坐标系课件(共20张PPT)
文档属性
| 名称 | 2021-2022七上 5.2平面直角坐标系课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 345.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
5.2 平面直角坐标系
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
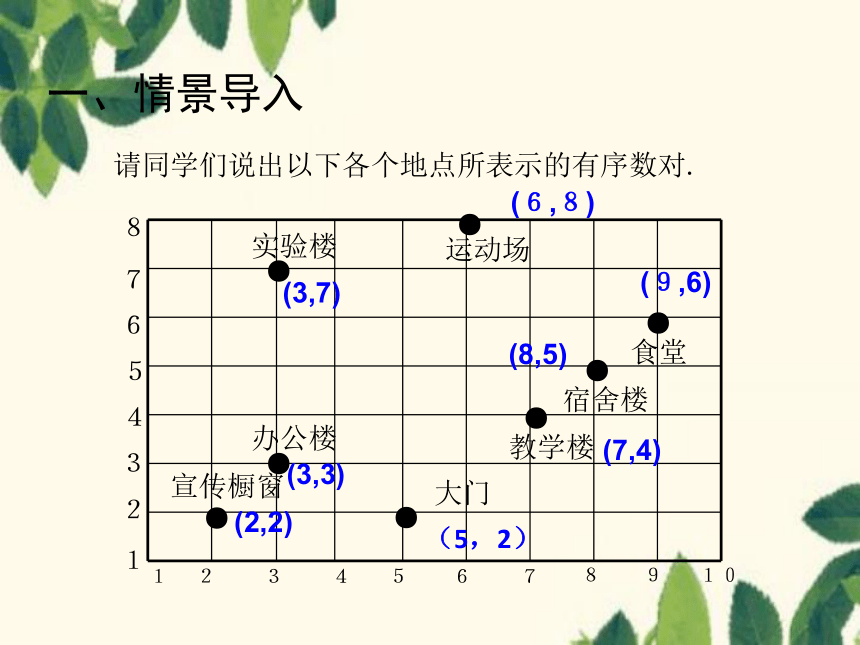
请同学们说出以下各个地点所表示的有序数对.
一、情景导入
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
A
B
C
D
E
F
G
A点是
(0,0)
B点是
(2,1)
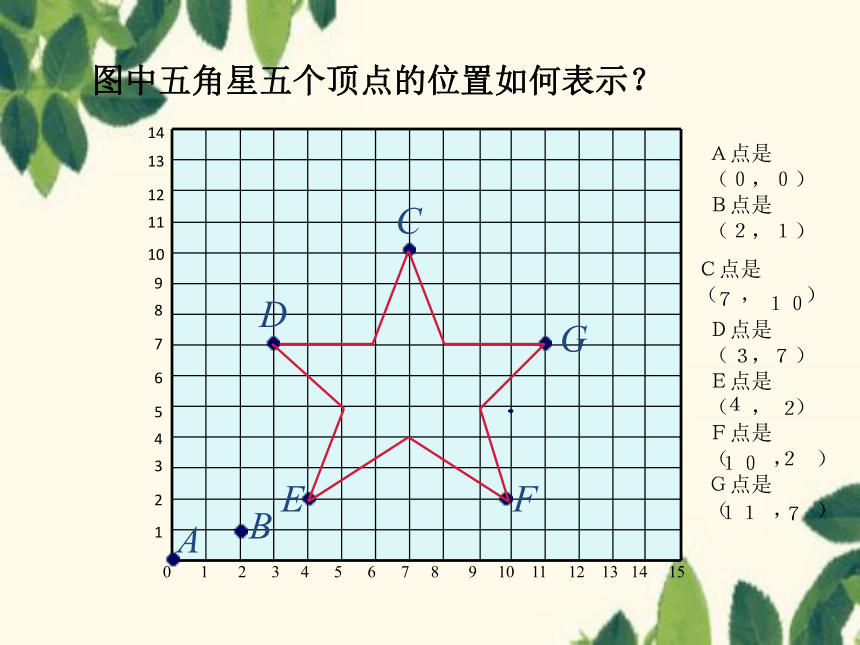
图中五角星五个顶点的位置如何表示?
C点是
( , )
D点是
( , )
E点是
( , )
F点是
( , )
G点是
( , )
7
10
3
7
4
10
2
11
7
2
1
3
4
5
6
2
7
14
11
12
13
8
9
10
学习目标
1.知识目标
(1)通过复习使学生掌握平面直角坐标系的相关概念;
(2)掌握坐标系中特殊位置点的坐标规律.
2.教学重点
相关知识的回顾,各种不同情境中点的坐标求法.
3.教学难点
较复杂背景中点的坐标求法.
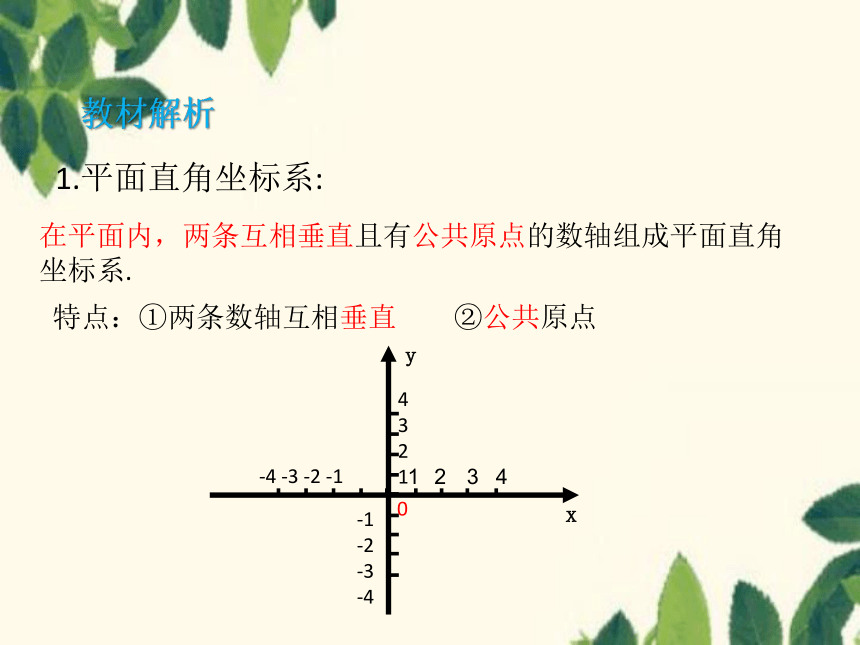
特点:①两条数轴互相垂直 ②公共原点
1.平面直角坐标系:
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
1
2
3
4
x
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
0
y
教材解析
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直
③公共原点 ,叫平面直角坐标系
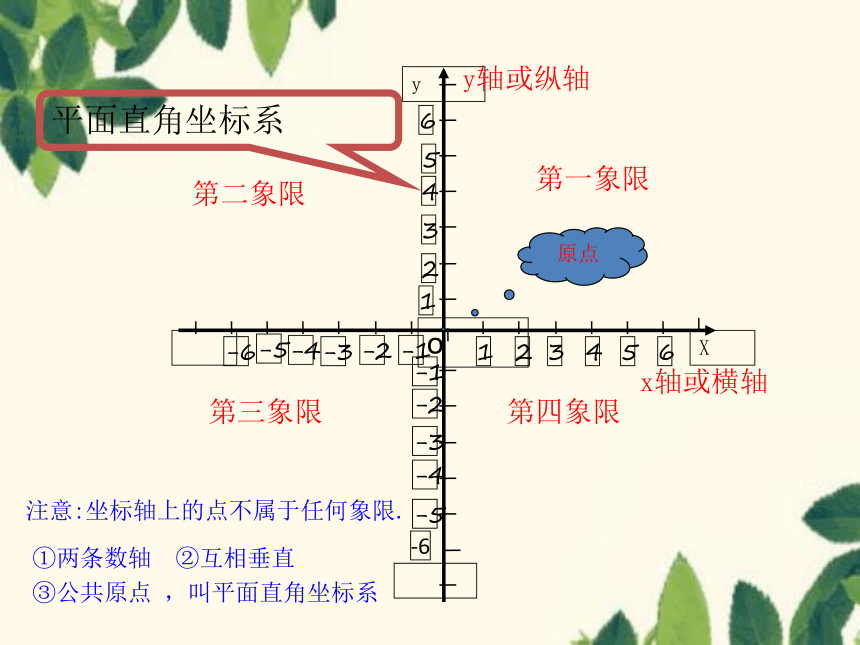
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
9
y
A
M
N
(7,8)
---------------------
﹉ ﹉ ﹉ ﹉ ﹉ ﹉ ﹉
O
-9
-8
-7
-6
-5
-4
-3
-2
-1
-1
-2
-3
-4
-5
-6
-7
-8
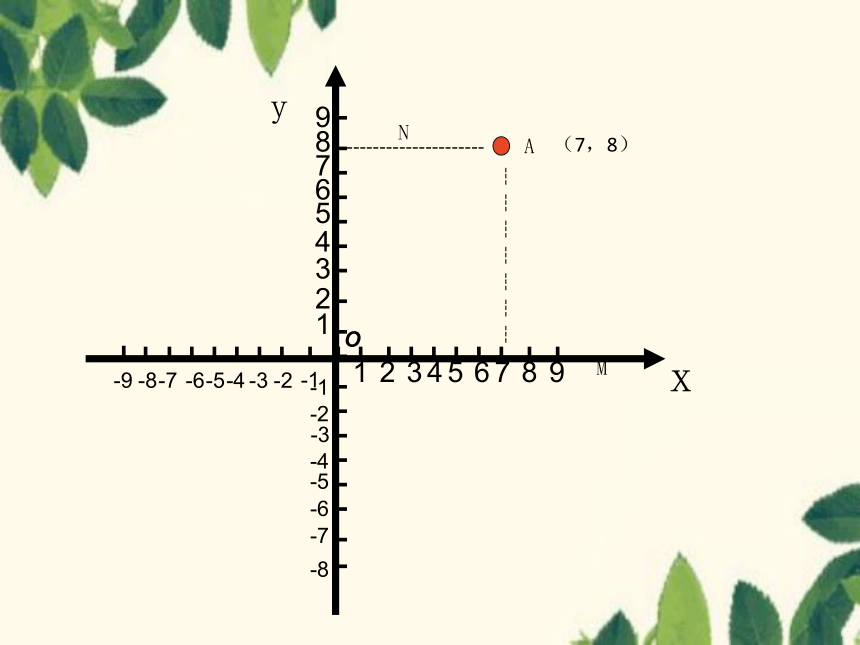
A点的坐标记作A(7,8).
1.过A点向x轴作垂线,垂足M在x轴上的坐标是7,
A点的横坐标为7;
2.过A点向y轴作垂线,垂足N 在y 轴上的坐标是8,
A点的纵坐标为8.
2.如何确定平面直角坐标系中点的坐标?
我们规定:横坐标在前,纵坐标在后
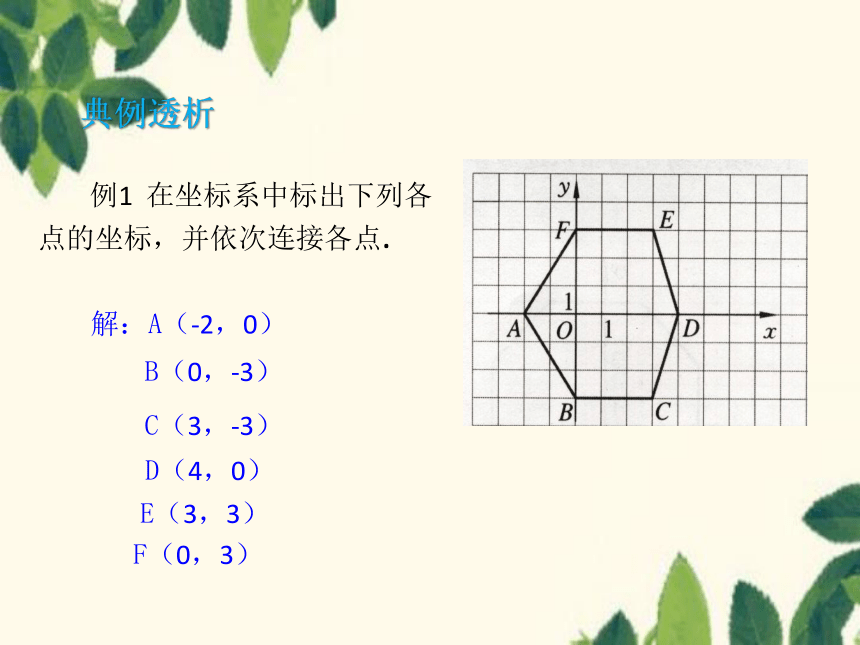
例1 在坐标系中标出下列各点的坐标,并依次连接各点.
解:A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
典例透析
1.点B与C的纵坐标相同,线段BC的位置有什么特点?
纵坐标相同的点的连线平行于x轴
2.线段CE的位置有什么特点?
横坐标相同的点的连线平行于y轴
3.坐标轴上的点的坐标有什么特点?
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
思考
例2 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的
坐标系,并写出各个顶点的坐标.
B
C
D
A
解: 如图,以点C为坐标
原点, 分别以CD , CB所
在的直线为x 轴,y 轴建
立直角坐标系. 此时C点
坐标为( 0 , 0 ).
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
由CD长为6, CB长为4,
可得D , B , A的坐标分
别为D( 6 , 0 ), B( 0 , 4 ),
A( 6 , 4 ) .
例3 一个直四棱柱的俯视图如图所示.请建立适当的坐标系,在直角坐标系中作出俯视图,并标出各顶点的坐标.
0
Y(cm)
X(cm)
解 建立直角坐标系如图,选择比例为1:10.取点E为直角坐标系的原点,使俯视图中的线段AB在x 轴上,
则可得A,B,C,D各点的坐标分别为(-1,0),(2,0),(2.5,1.5),(0,3.5).
根据上述坐标在直角坐标系中作点A、B、C、D,并用线段依次连结各点.如图就是所求作的俯视图.
A
B
C
D
(-1,0)
(2,0)
(2.5,1.5)
(0,3.5)
-1
1
2
1
2
3
A
B
C
D
100
200
200
150
50
E
单位:mm
1.写出图中A、B、C、D、E、F、O各点的坐标.
x
O
1
2
3
-1
-2
-3
-4
1
2
3
-1
-2
-3
y
4
A
B
C
D
E
F
跟踪练习
(4,3)
( - 4,1)
(-3,-3)
(3,-2)
(-2,0)
(0,2)
(0,0)
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
2. 在如图建立的直角坐标系中说出下列各点所表示的坐标
·
·
·
·
·
·
-4
-1
4
A
B
C
D
E
F
(0 , 6)
·
(-4,3)
(4,3)
(-2,3)
(2,3)
(-2,-3)
(2,-3)
M
3. 已知正方形的边长为4cm,按下列要求建立坐标系,确定正方形各顶点的坐标,并画出正方形
(1)取对角线的交点O为原点,AC在X轴上
(2)以A为原点,AB在X正半轴上
A
B
C
D
y
x
O
A
B
C
D
x
y
(2) A(0,0),B(4,0)C(4,4),D(0,4).
音乐喷泉
蜡像馆
蝴蝶园
绣湖
游乐场
O
x
1
2
1
2
-4
4
4
-3
3
3
-1
-1
-2
-2
y
如果直角坐标系的长度单位为1km,分别求“游乐场” “绣湖” 到“音乐喷泉” 的距离.
A
B
C
D
OC=
当堂检测
1.点(-1,2)在( )
A.第一象限 B.第二象限 C.第三象限 D. 第四象限
2.若点(X,Y)在第四象限内,则( )
A.X,Y同是正数 B.X,Y同是负数
C.X是正数,Y是负数 D.X是负数,Y是正数
3.横坐标是正数,纵坐标的绝对值是正数的点在( )
A.第一、三象限 B.第二、四象限
C.第二、三象限 D.第一、四象限
4.若点P(a,b)在第二象限,则点Q(-a,b+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
C
D
A
5.点 M(- 8,12)到 x轴的距离是 ,
到 y轴的距离是 .
6.若点P在第三象限且到x轴的距离为4,到y轴的距离为
1.5,则点P的坐标是 .
4.X轴上的点P到Y轴的距离为2.5,则点P的坐标为( )
A、(2.5,0) B 、(-2.5,0)
C、(0,2.5) D、(2.5,0)或(-2.5,0)
D
12
8
(-1.5, -4)
7. 如图正三角形ABC的边长为 6 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .
A
B
C
解: 如图,以边AB所在
的直线为x 轴,以边AB
的中垂线y 轴建立直角
坐标系.
y
x
o
( -3 , 0 )
( 3 , 0 )
6
3
1.坐标平面内的点与有序实数对是一一对应的.
2.给出坐标平面内的一点,可以用它所在象限或坐标轴来描述这个点所在平面内的位置.
3.要记住各象内点的坐标的符号,会根据对称的知识找出已知点关于坐标轴或原点的对称点.
小 结
5.2 平面直角坐标系
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
请同学们说出以下各个地点所表示的有序数对.
一、情景导入
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
A
B
C
D
E
F
G
A点是
(0,0)
B点是
(2,1)
图中五角星五个顶点的位置如何表示?
C点是
( , )
D点是
( , )
E点是
( , )
F点是
( , )
G点是
( , )
7
10
3
7
4
10
2
11
7
2
1
3
4
5
6
2
7
14
11
12
13
8
9
10
学习目标
1.知识目标
(1)通过复习使学生掌握平面直角坐标系的相关概念;
(2)掌握坐标系中特殊位置点的坐标规律.
2.教学重点
相关知识的回顾,各种不同情境中点的坐标求法.
3.教学难点
较复杂背景中点的坐标求法.
特点:①两条数轴互相垂直 ②公共原点
1.平面直角坐标系:
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
1
2
3
4
x
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
0
y
教材解析
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直
③公共原点 ,叫平面直角坐标系
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
9
y
A
M
N
(7,8)
---------------------
﹉ ﹉ ﹉ ﹉ ﹉ ﹉ ﹉
O
-9
-8
-7
-6
-5
-4
-3
-2
-1
-1
-2
-3
-4
-5
-6
-7
-8
A点的坐标记作A(7,8).
1.过A点向x轴作垂线,垂足M在x轴上的坐标是7,
A点的横坐标为7;
2.过A点向y轴作垂线,垂足N 在y 轴上的坐标是8,
A点的纵坐标为8.
2.如何确定平面直角坐标系中点的坐标?
我们规定:横坐标在前,纵坐标在后
例1 在坐标系中标出下列各点的坐标,并依次连接各点.
解:A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
典例透析
1.点B与C的纵坐标相同,线段BC的位置有什么特点?
纵坐标相同的点的连线平行于x轴
2.线段CE的位置有什么特点?
横坐标相同的点的连线平行于y轴
3.坐标轴上的点的坐标有什么特点?
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
思考
例2 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的
坐标系,并写出各个顶点的坐标.
B
C
D
A
解: 如图,以点C为坐标
原点, 分别以CD , CB所
在的直线为x 轴,y 轴建
立直角坐标系. 此时C点
坐标为( 0 , 0 ).
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
由CD长为6, CB长为4,
可得D , B , A的坐标分
别为D( 6 , 0 ), B( 0 , 4 ),
A( 6 , 4 ) .
例3 一个直四棱柱的俯视图如图所示.请建立适当的坐标系,在直角坐标系中作出俯视图,并标出各顶点的坐标.
0
Y(cm)
X(cm)
解 建立直角坐标系如图,选择比例为1:10.取点E为直角坐标系的原点,使俯视图中的线段AB在x 轴上,
则可得A,B,C,D各点的坐标分别为(-1,0),(2,0),(2.5,1.5),(0,3.5).
根据上述坐标在直角坐标系中作点A、B、C、D,并用线段依次连结各点.如图就是所求作的俯视图.
A
B
C
D
(-1,0)
(2,0)
(2.5,1.5)
(0,3.5)
-1
1
2
1
2
3
A
B
C
D
100
200
200
150
50
E
单位:mm
1.写出图中A、B、C、D、E、F、O各点的坐标.
x
O
1
2
3
-1
-2
-3
-4
1
2
3
-1
-2
-3
y
4
A
B
C
D
E
F
跟踪练习
(4,3)
( - 4,1)
(-3,-3)
(3,-2)
(-2,0)
(0,2)
(0,0)
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
2. 在如图建立的直角坐标系中说出下列各点所表示的坐标
·
·
·
·
·
·
-4
-1
4
A
B
C
D
E
F
(0 , 6)
·
(-4,3)
(4,3)
(-2,3)
(2,3)
(-2,-3)
(2,-3)
M
3. 已知正方形的边长为4cm,按下列要求建立坐标系,确定正方形各顶点的坐标,并画出正方形
(1)取对角线的交点O为原点,AC在X轴上
(2)以A为原点,AB在X正半轴上
A
B
C
D
y
x
O
A
B
C
D
x
y
(2) A(0,0),B(4,0)C(4,4),D(0,4).
音乐喷泉
蜡像馆
蝴蝶园
绣湖
游乐场
O
x
1
2
1
2
-4
4
4
-3
3
3
-1
-1
-2
-2
y
如果直角坐标系的长度单位为1km,分别求“游乐场” “绣湖” 到“音乐喷泉” 的距离.
A
B
C
D
OC=
当堂检测
1.点(-1,2)在( )
A.第一象限 B.第二象限 C.第三象限 D. 第四象限
2.若点(X,Y)在第四象限内,则( )
A.X,Y同是正数 B.X,Y同是负数
C.X是正数,Y是负数 D.X是负数,Y是正数
3.横坐标是正数,纵坐标的绝对值是正数的点在( )
A.第一、三象限 B.第二、四象限
C.第二、三象限 D.第一、四象限
4.若点P(a,b)在第二象限,则点Q(-a,b+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
C
D
A
5.点 M(- 8,12)到 x轴的距离是 ,
到 y轴的距离是 .
6.若点P在第三象限且到x轴的距离为4,到y轴的距离为
1.5,则点P的坐标是 .
4.X轴上的点P到Y轴的距离为2.5,则点P的坐标为( )
A、(2.5,0) B 、(-2.5,0)
C、(0,2.5) D、(2.5,0)或(-2.5,0)
D
12
8
(-1.5, -4)
7. 如图正三角形ABC的边长为 6 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .
A
B
C
解: 如图,以边AB所在
的直线为x 轴,以边AB
的中垂线y 轴建立直角
坐标系.
y
x
o
( -3 , 0 )
( 3 , 0 )
6
3
1.坐标平面内的点与有序实数对是一一对应的.
2.给出坐标平面内的一点,可以用它所在象限或坐标轴来描述这个点所在平面内的位置.
3.要记住各象内点的坐标的符号,会根据对称的知识找出已知点关于坐标轴或原点的对称点.
小 结
