2021-2022七上 2.4利用轴对称进行设计课件(共24张PPT)
文档属性
| 名称 | 2021-2022七上 2.4利用轴对称进行设计课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 716.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
2.4 利用轴对称进行设计
剪纸艺术
情境引入
实物图案
花边艺术
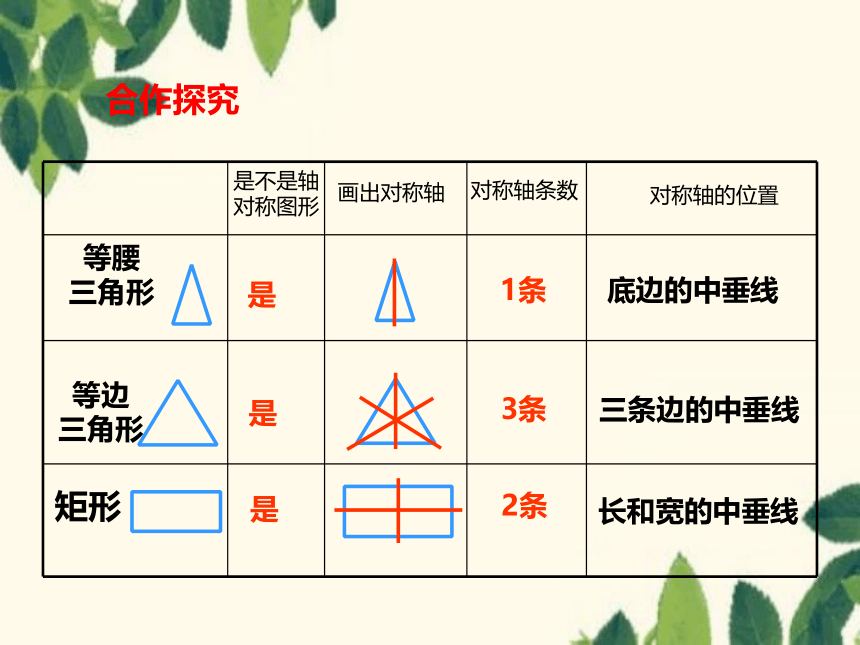
矩形
等边 三角形
对称轴条数
3条
2条
对称轴的位置
长和宽的中垂线
三条边的中垂线
等腰 三角形
画出对称轴
1条
底边的中垂线
是不是轴对称图形
是
是
是
合作探究
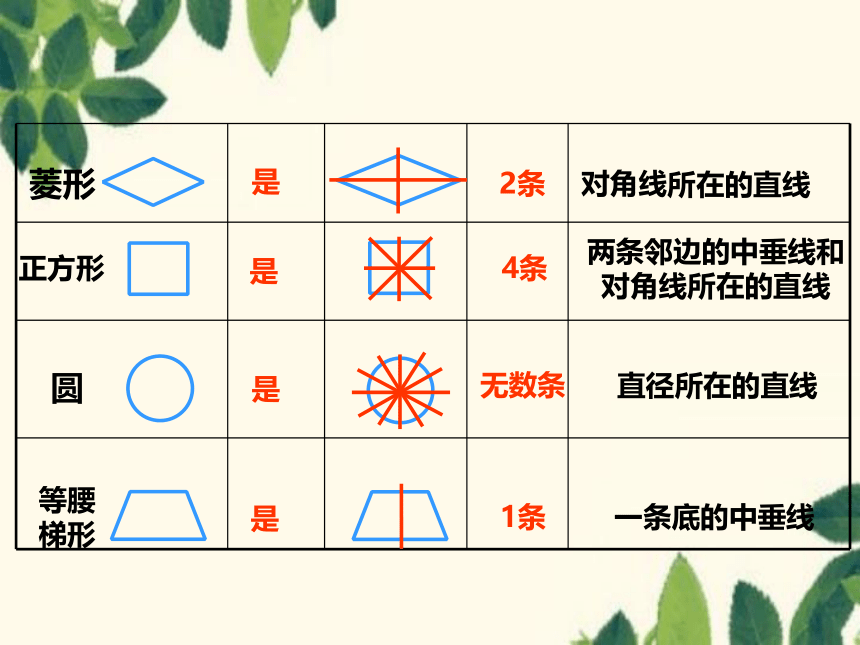
正方形
菱形
圆
等腰梯形
4条
1条
无数条
2条
两条邻边的中垂线和对角线所在的直线
对角线
直径所在的直线
一条底的中垂线
所在的直线
是
是
是
是
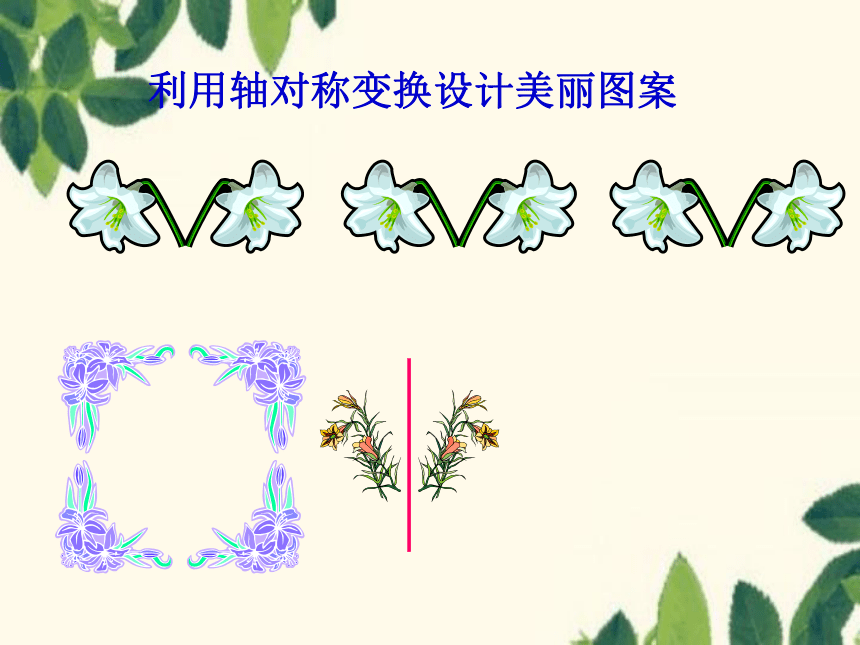
利用轴对称变换设计美丽图案
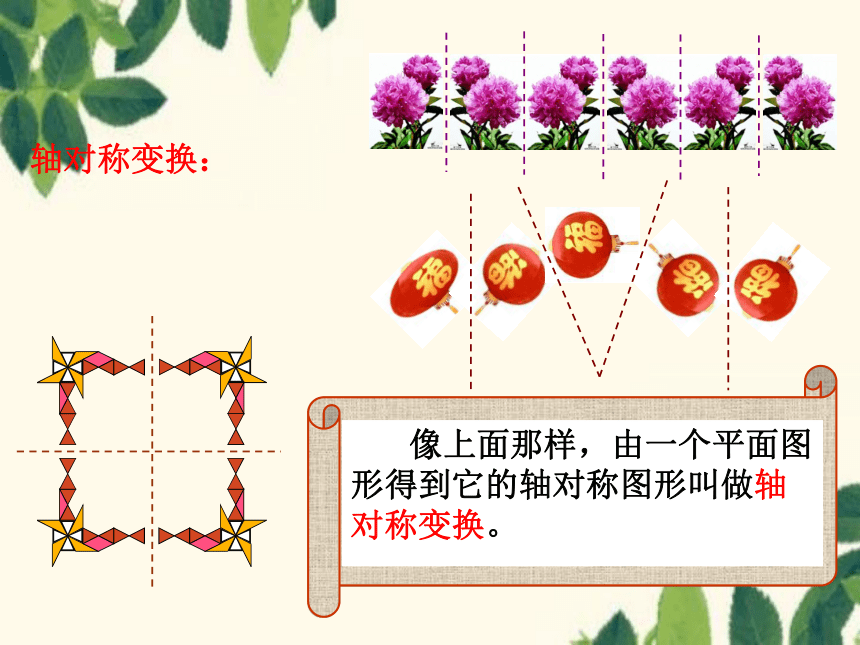
像上面那样,由一个平面图形得到它的轴对称图形叫做轴对称变换。
轴对称变换:
已知对称轴 l 和一个点A如
何画出点A关于 l 的对称点A’
3、点 A’ 就是点A关于l的对称点.
A
A’
1、过点A作对称轴 l 的垂线,垂足为O
2、在垂线上截取0A=OA’
o
l
∴点A’即为所求
如何画线段AB关于直线 的
对称线段A’B’
找关键点,一一作出其对称点!
然后连结线段.
A
B
∴线段A’B’即为所求
A’
B’
∴△A’B’C’即为所求。
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
A
B
C
A’
B’
C’
例题学习
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点);
(画出特殊点关于已知直线的对称点);
(连接对称点)。
A
B
C
A’
B’
C’
如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
A
B
C
A
B
C
A
B
C
A
B
C
B’’
C’’
A’’
M′
N′
如图,把下面的图形补成关于直线l对称的图形.
l
如图,把下面的图形补成关于直线l对称的图形.
l
由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的____________ 完全一样;
新图形上的每一点,都是原图形上的某一点关于直线l的______;
连接任意一对对应点的线段被对称轴_________。
l
P
P’
轴对称变换的性质:
形状大小
对称点
垂直平分
纳
归
一
课堂小结
1、成轴对称的两个图形可以看作由其中一个图形经过 得到的。
纳
归
二
2、轴对称图形也可以看作是由其中一部分经过 扩展得到的。
轴对称变换
轴对称变换
1仔细观察下列图案,并按规律在横线上画出合适的图形.
巩固训练
2在由小正方形围成的L形图中,请你用三种方法分别添画一个小正方形,使它成为轴对称图形。
3 传说亚历山大城有一位精通数学和物理的学者,名叫海伦。一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
军官每天从军营A出发先到河边P处饮马,然后再去河岸同侧的B地去开会,应该怎样走才能使路程最短?
河
如图所示,将军从山脚下的A点出发,走到河旁边的P点饮马后再到B点开会.请问怎样走才能使总的路程最短?
A
B
A`
p
4 某开发区新建了两片住宅区:A区、B区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短
A小区
B 小区
煤气主管道
l
B
A
P
A'
P'
作法:
1.作点A关于直线l的对称点 A’;
5已知:直线l和l的同侧两点A、B.
2.连结A’B,交l于点 P.
∴ 点P就是所求的点.
求作:点P,使它在直线l上,并使AP+BP最小.
2.4 利用轴对称进行设计
剪纸艺术
情境引入
实物图案
花边艺术
矩形
等边 三角形
对称轴条数
3条
2条
对称轴的位置
长和宽的中垂线
三条边的中垂线
等腰 三角形
画出对称轴
1条
底边的中垂线
是不是轴对称图形
是
是
是
合作探究
正方形
菱形
圆
等腰梯形
4条
1条
无数条
2条
两条邻边的中垂线和对角线所在的直线
对角线
直径所在的直线
一条底的中垂线
所在的直线
是
是
是
是
利用轴对称变换设计美丽图案
像上面那样,由一个平面图形得到它的轴对称图形叫做轴对称变换。
轴对称变换:
已知对称轴 l 和一个点A如
何画出点A关于 l 的对称点A’
3、点 A’ 就是点A关于l的对称点.
A
A’
1、过点A作对称轴 l 的垂线,垂足为O
2、在垂线上截取0A=OA’
o
l
∴点A’即为所求
如何画线段AB关于直线 的
对称线段A’B’
找关键点,一一作出其对称点!
然后连结线段.
A
B
∴线段A’B’即为所求
A’
B’
∴△A’B’C’即为所求。
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
A
B
C
A’
B’
C’
例题学习
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点);
(画出特殊点关于已知直线的对称点);
(连接对称点)。
A
B
C
A’
B’
C’
如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
A
B
C
A
B
C
A
B
C
A
B
C
B’’
C’’
A’’
M′
N′
如图,把下面的图形补成关于直线l对称的图形.
l
如图,把下面的图形补成关于直线l对称的图形.
l
由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的____________ 完全一样;
新图形上的每一点,都是原图形上的某一点关于直线l的______;
连接任意一对对应点的线段被对称轴_________。
l
P
P’
轴对称变换的性质:
形状大小
对称点
垂直平分
纳
归
一
课堂小结
1、成轴对称的两个图形可以看作由其中一个图形经过 得到的。
纳
归
二
2、轴对称图形也可以看作是由其中一部分经过 扩展得到的。
轴对称变换
轴对称变换
1仔细观察下列图案,并按规律在横线上画出合适的图形.
巩固训练
2在由小正方形围成的L形图中,请你用三种方法分别添画一个小正方形,使它成为轴对称图形。
3 传说亚历山大城有一位精通数学和物理的学者,名叫海伦。一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
军官每天从军营A出发先到河边P处饮马,然后再去河岸同侧的B地去开会,应该怎样走才能使路程最短?
河
如图所示,将军从山脚下的A点出发,走到河旁边的P点饮马后再到B点开会.请问怎样走才能使总的路程最短?
A
B
A`
p
4 某开发区新建了两片住宅区:A区、B区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短
A小区
B 小区
煤气主管道
l
B
A
P
A'
P'
作法:
1.作点A关于直线l的对称点 A’;
5已知:直线l和l的同侧两点A、B.
2.连结A’B,交l于点 P.
∴ 点P就是所求的点.
求作:点P,使它在直线l上,并使AP+BP最小.
