探索勾股定理

(共14张PPT)
探索勾股定理
八年级数学（上册） 北师大版
观察左图
正方形A中含有 个小方格，即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
16
25
1
2
3
C
B
A
A、B、C的面积有什么关系？
1
2
3
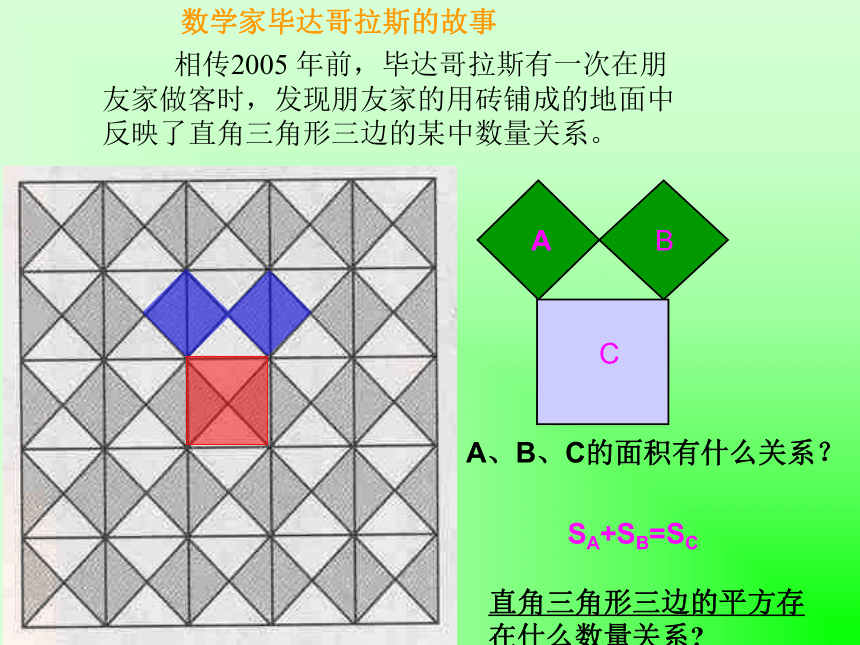
　　数学家毕达哥拉斯的故事
相传2005 年前，毕达哥拉斯有一次在朋友家做客时，发现朋友家的用砖铺成的地面中反映了直角三角形三边的某中数量关系。
A
B
C
A、B、C的面积有什么关系？
SA+SB=SC
直角三角形三边的平方存在什么数量关系
A
B
C
A
B
C
（图中每个小方格代表一个单位面积）
图1-1
图1-2
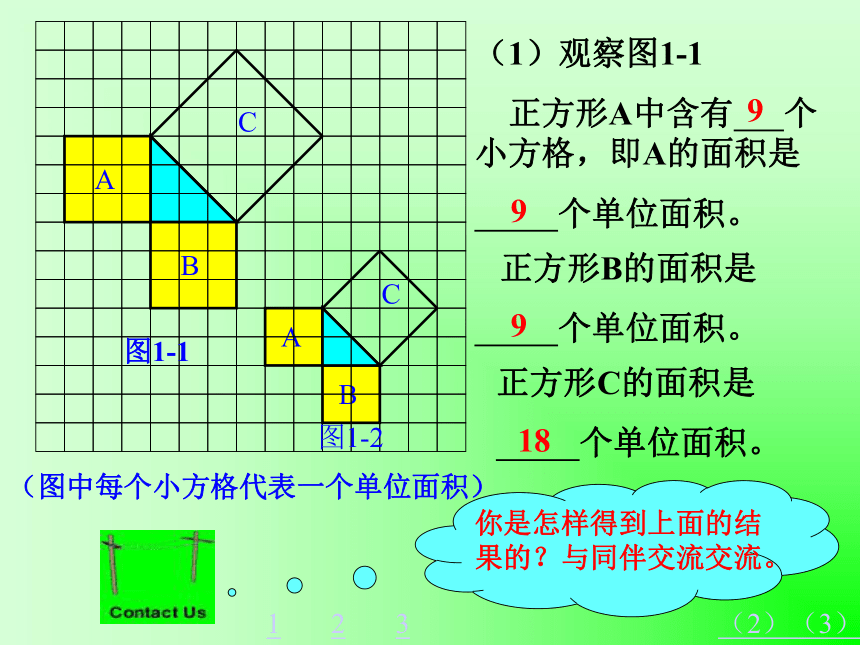
（1）观察图1-1
正方形A中含有 个小方格，即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
你是怎样得到上面的结果的？与同伴交流交流。
1
2
3
（2）（3）
A
B
C
A
B
C
（图中每个小方格代表一个单位面积）
图1-1
图1-2
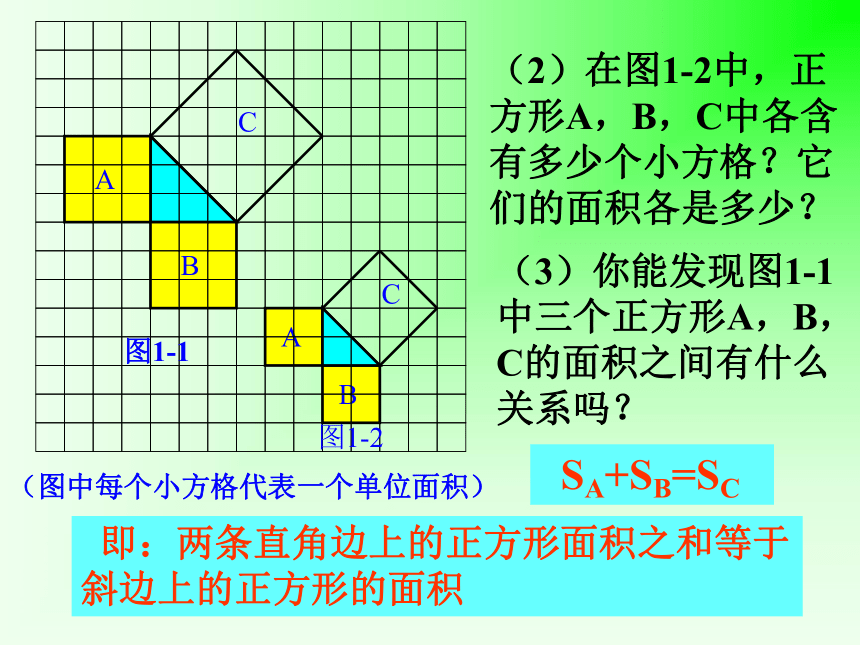
（2）在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？
（3）你能发现图1-1中三个正方形A，B，C的面积之间有什么关系吗？
SA+SB=SC
即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积
A
B
C
图1-3
A
B
C
图1-4
（1）观察图1-3、图1-4，并填写右表：
A的面积（单位面积）
B的面积（单位面积）
C的面积（单位面积）
图1-3
图1-4
16
9
25
4
9
13
你是怎样得到表中的结果的？与同伴交流交流。
做一做
幻灯片 9
A
B
C
图1-3
A
B
C
图1-4
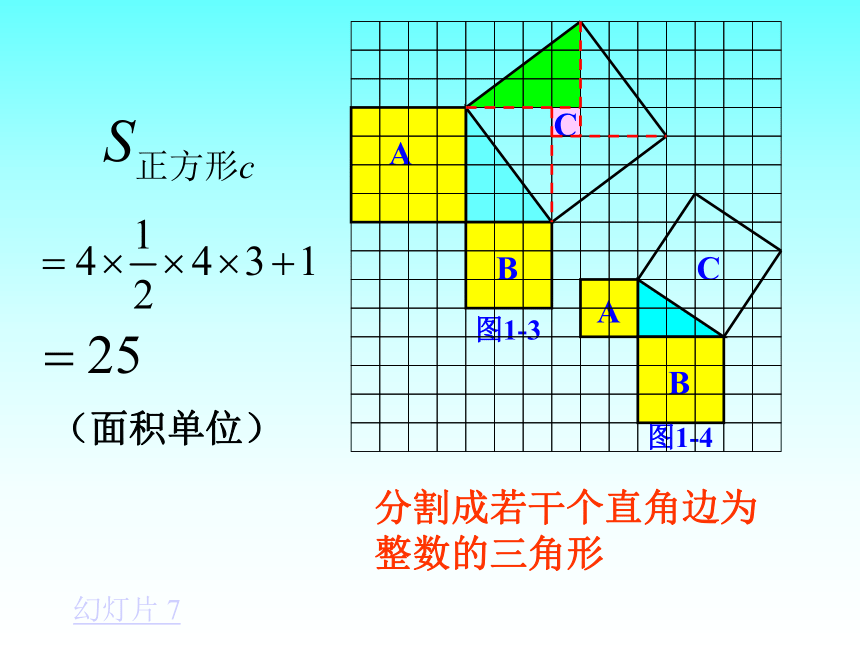
分割成若干个直角边为整数的三角形
（面积单位）
幻灯片 7
A
B
C
图1-3
A
B
C
图1-4
（2）三个正方形A，B，C的面积之间有什么关系？
SA+SB=SC
即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积
幻灯片 7
A
B
C
图1-3
A
B
C
图1-4
（1）你能用三角形的边长表示正方形的面积吗？
（2）你能发现直角三角形三边长度之间存在什么关系吗？与同伴进行交流。
（3）分别以5厘米、12厘米为直角边作出一个直角三角形，并测量斜边的长度。（2）中的规律对这个三角形仍然成立吗？
议一议
勾股定理（gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c，那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理耶！
想一想
1、如图，受台风麦莎影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？
4米
3米
小结
说说这节课你有什么收获？
作业
一、P7 习题1.1 第1题
二、准备4张全等的直角三角形纸片
a
b
c
再见