2021-2022学年苏科新版九年级上册数学《第2章 对称图形——圆》单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科新版九年级上册数学《第2章 对称图形——圆》单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 403.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 07:16:17 | ||
图片预览


文档简介
2021-2022学年苏科新版九年级上册数学《第2章 对称图形——圆》单元测试卷
一.选择题
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
2.下列图形中面积最大的是( )
A.边长为5的正方形
B.半径为的圆
C.边长分别为6,8,10的直角三角形
D.边长为7的正三角形
3.下列说法不正确的是( )
A.只有当x=1时,分式的值才为零
B.与2是同类二次根式
C.等腰三角形底边上的中线与底边上的高重合
D.三点确定一个圆
4.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A. B.2 C.2 D.3
5.如图,正方形的边长为a,以各边为直径在正方形内画半圆,所围成的图形(阴影部分)的面积为( )
A.πa2﹣a2 B.2πa2﹣a2 C.πa2﹣a2 D.a2﹣πa2
6.若⊙P的半径为5,圆心P的坐标为(﹣3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
7.《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响.在《九章算术》中有很多名题,下面就是其中的一道.原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,CD为⊙O的直径,弦AB⊥CD于点E.CE=1寸,AB=10寸,则可得直径CD的长为( )
A.13寸 B.26寸 C.18寸 D.24寸
8.下列命题是真命题的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.两边及一边的对角对应相等的两个三角形全等
C.三点确定一个圆
D.若a>b,c>0,则ac>bc
9.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,OC=3,则EC的长为( )
A. B.8 C. D.
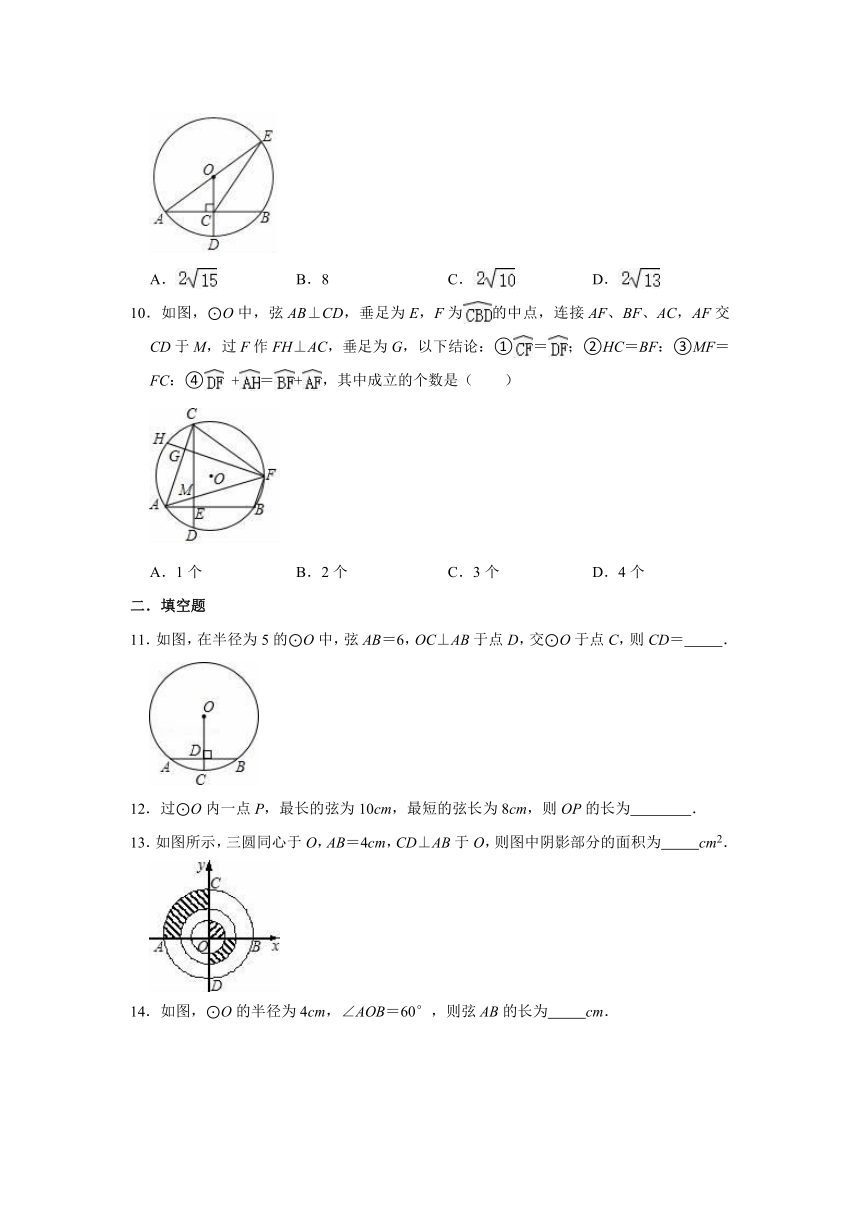
10.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④ +=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,在半径为5的⊙O中,弦AB=6,OC⊥AB于点D,交⊙O于点C,则CD= .
12.过⊙O内一点P,最长的弦为10cm,最短的弦长为8cm,则OP的长为 .
13.如图所示,三圆同心于O,AB=4cm,CD⊥AB于O,则图中阴影部分的面积为 cm2.
14.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 cm.
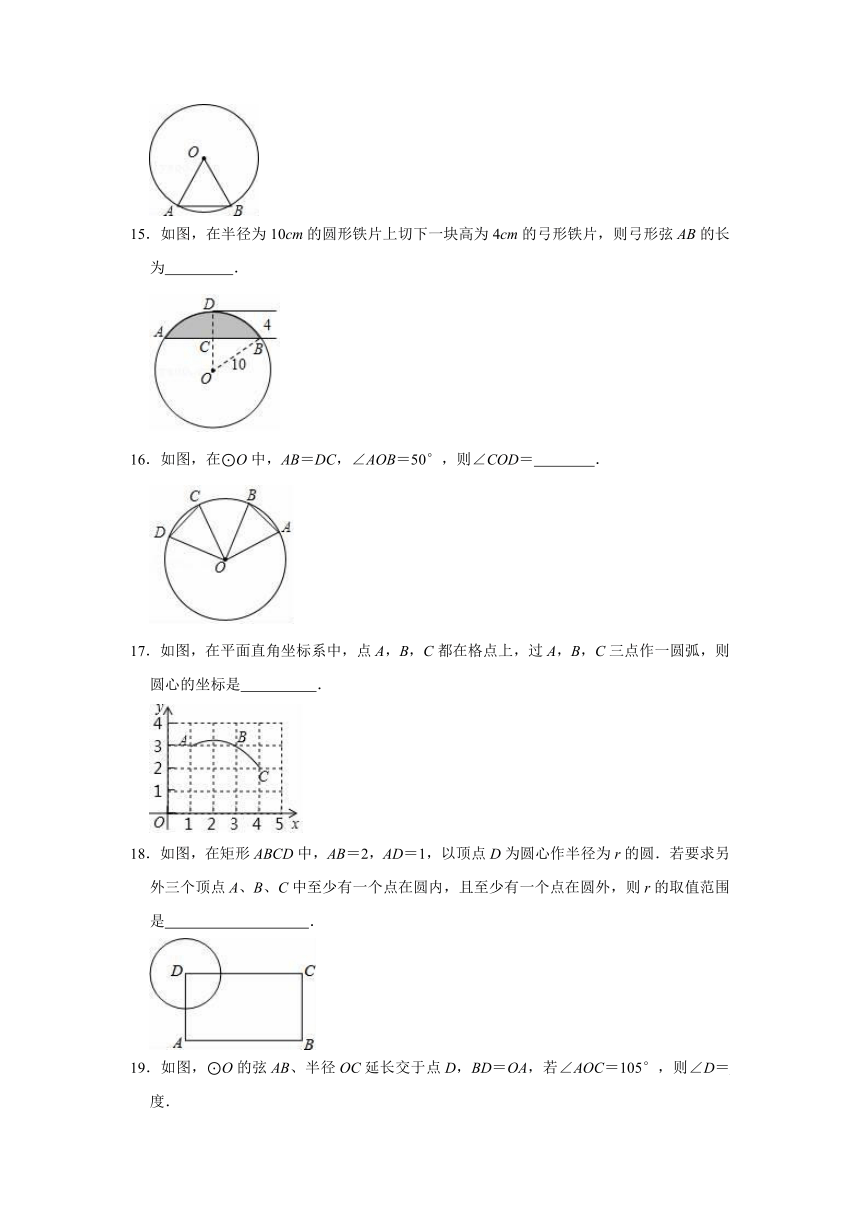
15.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 .
16.如图,在⊙O中,AB=DC,∠AOB=50°,则∠COD= .
17.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
18.如图,在矩形ABCD中,AB=2,AD=1,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
19.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
20.正方形的四个顶点和它的中心共5个点能确定 个不同的圆.
三.解答题
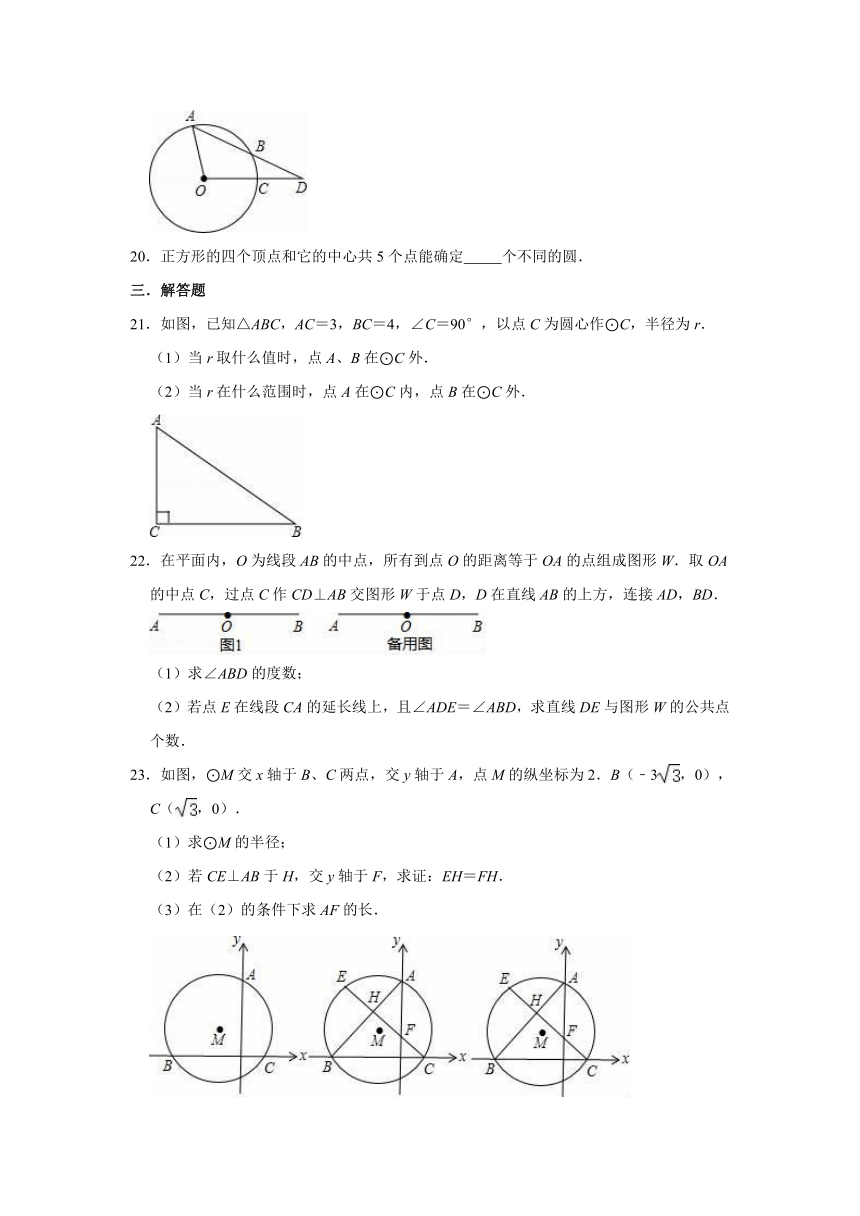
21.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
22.在平面内,O为线段AB的中点,所有到点O的距离等于OA的点组成图形W.取OA的中点C,过点C作CD⊥AB交图形W于点D,D在直线AB的上方,连接AD,BD.
(1)求∠ABD的度数;
(2)若点E在线段CA的延长线上,且∠ADE=∠ABD,求直线DE与图形W的公共点个数.
23.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
24.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5 m(手臂与拉直的绳子在一条直线上)手臂肩部距地面1.5 m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
25.如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
(1)求线段OD的长;
(2)当EO=BE时,求DE的长.
26.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
27.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
参考答案与试题解析
一.选择题
1.解:连接OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选:B.
2.解:A:S=5×5=25;
B:S=π()2=25.12;
C:S=×6×8=24;
D:边长为7的正三角形中高为7 sin60°,
S=×7×7 sin60°=×49×=21.217.
B的面积最大,故选B.
3.解:A、x2﹣1=0且x+1≠00,解得:x=1,故正确;
B、=3,2=,故正确;
C、根据三线合一定理可得.故正确;
D、因为不在同一直线的三点确定一个圆,故D错误.
故选:D.
4.解:过O作OC⊥AB于C,
∵OA=OB=4,∠AOB=90°,
∴AB=OA=4,
∴OC=AB=2,
故选:C.
5.解:x和y如图所示,则
解得4x=πa2﹣a2,即阴影部分的面积为πa2﹣a2.
故选:C.
6.解:由勾股定理,得
OP==5,
d=r=5,
原点O在⊙P上.
故选:B.
7.解:连接OA,AB⊥CD,
由垂径定理知,点E是AB的中点,AE=AB=5,OE=OC﹣CE=OA﹣CE,
设半径为r寸,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2,
即r2=52+(r﹣1)2,
解得:r=13,
所以CD=2r=26,
即圆的直径为26寸.
故选:B.
8.解:A、一组对边相等,另一组对边平行的四边形有可能是等腰梯形,故原命题错误;
B、符合SSA的两个三角形不一定全等,故命题错误;
C、不在同一直线上的三点确定一个圆,故错误;
D、若a>b,c>0,则ac>bc,故正确.
故选:D.
9.解:连接BE,
∵AE为⊙O直径,
∴∠ABE=90°,
∵OD⊥AB,OD过O,
∴AC=BC=AB==4,
∵AO=OE,
∴BE=2OC,
∵OC=3,
∴BE=6,
在Rt△CBE中,EC===2,
故选:D.
10.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠FCG=∠ACM+∠GCM,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
二.填空题
11.解:连接OA,
∵AB=6,OC⊥AB于点D,
∴AD=AB=×6=3,
∵⊙O的半径为5,
∴OD===4,
∴CD=OC﹣OD=5﹣4=1.
故答案为:1.
12.解:如图所示,CD⊥AB于点P.
根据题意,得
AB=10cm,CD=6cm.
∵CD⊥AB,
∴CP=CD=4cm.
根据勾股定理,得OP===3(cm).
故答案为:3cm.
13.解:阴影部分的面积应等于=圆=π(4÷2)2=πcm2.
14.解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
15.解:如图,过O作OD⊥AB于C,交⊙O于D
∵CD=4cm,OD=10cm,
∴OC=6cm,
又∵OB=10cm,
∴Rt△BCO中,BC==8(cm),
∴AB=2BC=16cm.
故答案为:16cm.
16.解:∵AB=CD,
∴∠COD=∠AOB,
∵∠AOB=50°,
∴∠COD=50°,
故答案是:50°.
17.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
18.解:在直角△ABD中,CD=AB=2,AD=1,
则BD==.
由图可知1<r<.
故答案为:1<r<.
19.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
20.解:正方形的四个顶点和它的中心的点的距离相等,中心与一边的两个端点可以确定一个圆,正方形有四条边,因而有四个圆;而正方形的四个顶点都在以中心为圆心的圆上,因而能确定5个不同的圆.
三.解答题
21.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
22.解:(1)根据题意,图形W为以O为圆心,OA为直径的圆.
如图1,连接OD,
∴OA=OD.
∵点C为OA的中点,CD⊥AB,
∴AD=OD.
∴OA=OD=AD.
∴△OAD 是等边三角形.
∴∠AOD=60°.
∴∠ABD=30°.
(2)如图2,
∵∠ADE=∠ABD,
∴∠ADE=30°.
∵∠ADO=60°.
∴∠ODE=90°.
∴OD⊥DE.
∴DE是⊙O的切线.
∴直线DE与图形W的公共点个数为1.
23.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
24.解:由题意可知AB=2.5m,AC=1.5m,
小狗在地平面上环绕跑圆的半径为=2.0(m),
小狗活动的区域是以2.0m为半径的圆,如图.
25.解:(1)连接OB.
∵OD过圆心,且D是弦BC中点,
∴OD⊥BC,BD=BC,
在Rt△BOD中,OD2+BD2=BO2.
∵BO=AO=8,BD=6.
∴OD=2;
(2)在Rt△EOD中,OD2+ED2=EO2.
设BE=x,则OE=x,DE=6﹣x.
(2)2+(6﹣x)2=(x)2,
解得x1=﹣16(舍),x2=4.
则DE=2.
26.解:连接OA、OC,
∵由题意知:AB∥CD,OE⊥AB,OF⊥CD,CD=20cm,
∴CG=CD=10cm,
在Rt△OGC中,由勾股定理得:OC2=CG2+OG2,
OC2=102+(OC﹣2)2,
解得:OC=26(cm),
则OE=26cm﹣2cm﹣2cm=22cm,
∵在Rt△OEA中,由勾股定理得:OA2=OE2+AE2,
∴262=222+AE2,
∴AE=8,
∵OE⊥AB,OE过圆心O,
∴AB=2AE=16cm.
27.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
一.选择题
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
2.下列图形中面积最大的是( )
A.边长为5的正方形
B.半径为的圆
C.边长分别为6,8,10的直角三角形
D.边长为7的正三角形
3.下列说法不正确的是( )
A.只有当x=1时,分式的值才为零
B.与2是同类二次根式
C.等腰三角形底边上的中线与底边上的高重合
D.三点确定一个圆
4.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A. B.2 C.2 D.3
5.如图,正方形的边长为a,以各边为直径在正方形内画半圆,所围成的图形(阴影部分)的面积为( )
A.πa2﹣a2 B.2πa2﹣a2 C.πa2﹣a2 D.a2﹣πa2
6.若⊙P的半径为5,圆心P的坐标为(﹣3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
7.《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响.在《九章算术》中有很多名题,下面就是其中的一道.原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,CD为⊙O的直径,弦AB⊥CD于点E.CE=1寸,AB=10寸,则可得直径CD的长为( )
A.13寸 B.26寸 C.18寸 D.24寸
8.下列命题是真命题的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.两边及一边的对角对应相等的两个三角形全等
C.三点确定一个圆
D.若a>b,c>0,则ac>bc
9.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,OC=3,则EC的长为( )
A. B.8 C. D.
10.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④ +=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,在半径为5的⊙O中,弦AB=6,OC⊥AB于点D,交⊙O于点C,则CD= .
12.过⊙O内一点P,最长的弦为10cm,最短的弦长为8cm,则OP的长为 .
13.如图所示,三圆同心于O,AB=4cm,CD⊥AB于O,则图中阴影部分的面积为 cm2.
14.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 cm.
15.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 .
16.如图,在⊙O中,AB=DC,∠AOB=50°,则∠COD= .
17.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
18.如图,在矩形ABCD中,AB=2,AD=1,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
19.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
20.正方形的四个顶点和它的中心共5个点能确定 个不同的圆.
三.解答题
21.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
22.在平面内,O为线段AB的中点,所有到点O的距离等于OA的点组成图形W.取OA的中点C,过点C作CD⊥AB交图形W于点D,D在直线AB的上方,连接AD,BD.
(1)求∠ABD的度数;
(2)若点E在线段CA的延长线上,且∠ADE=∠ABD,求直线DE与图形W的公共点个数.
23.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
24.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5 m(手臂与拉直的绳子在一条直线上)手臂肩部距地面1.5 m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
25.如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
(1)求线段OD的长;
(2)当EO=BE时,求DE的长.
26.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
27.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
参考答案与试题解析
一.选择题
1.解:连接OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选:B.
2.解:A:S=5×5=25;
B:S=π()2=25.12;
C:S=×6×8=24;
D:边长为7的正三角形中高为7 sin60°,
S=×7×7 sin60°=×49×=21.217.
B的面积最大,故选B.
3.解:A、x2﹣1=0且x+1≠00,解得:x=1,故正确;
B、=3,2=,故正确;
C、根据三线合一定理可得.故正确;
D、因为不在同一直线的三点确定一个圆,故D错误.
故选:D.
4.解:过O作OC⊥AB于C,
∵OA=OB=4,∠AOB=90°,
∴AB=OA=4,
∴OC=AB=2,
故选:C.
5.解:x和y如图所示,则
解得4x=πa2﹣a2,即阴影部分的面积为πa2﹣a2.
故选:C.
6.解:由勾股定理,得
OP==5,
d=r=5,
原点O在⊙P上.
故选:B.
7.解:连接OA,AB⊥CD,
由垂径定理知,点E是AB的中点,AE=AB=5,OE=OC﹣CE=OA﹣CE,
设半径为r寸,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2,
即r2=52+(r﹣1)2,
解得:r=13,
所以CD=2r=26,
即圆的直径为26寸.
故选:B.
8.解:A、一组对边相等,另一组对边平行的四边形有可能是等腰梯形,故原命题错误;
B、符合SSA的两个三角形不一定全等,故命题错误;
C、不在同一直线上的三点确定一个圆,故错误;
D、若a>b,c>0,则ac>bc,故正确.
故选:D.
9.解:连接BE,
∵AE为⊙O直径,
∴∠ABE=90°,
∵OD⊥AB,OD过O,
∴AC=BC=AB==4,
∵AO=OE,
∴BE=2OC,
∵OC=3,
∴BE=6,
在Rt△CBE中,EC===2,
故选:D.
10.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠FCG=∠ACM+∠GCM,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
二.填空题
11.解:连接OA,
∵AB=6,OC⊥AB于点D,
∴AD=AB=×6=3,
∵⊙O的半径为5,
∴OD===4,
∴CD=OC﹣OD=5﹣4=1.
故答案为:1.
12.解:如图所示,CD⊥AB于点P.
根据题意,得
AB=10cm,CD=6cm.
∵CD⊥AB,
∴CP=CD=4cm.
根据勾股定理,得OP===3(cm).
故答案为:3cm.
13.解:阴影部分的面积应等于=圆=π(4÷2)2=πcm2.
14.解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
15.解:如图,过O作OD⊥AB于C,交⊙O于D
∵CD=4cm,OD=10cm,
∴OC=6cm,
又∵OB=10cm,
∴Rt△BCO中,BC==8(cm),
∴AB=2BC=16cm.
故答案为:16cm.
16.解:∵AB=CD,
∴∠COD=∠AOB,
∵∠AOB=50°,
∴∠COD=50°,
故答案是:50°.
17.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
18.解:在直角△ABD中,CD=AB=2,AD=1,
则BD==.
由图可知1<r<.
故答案为:1<r<.
19.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
20.解:正方形的四个顶点和它的中心的点的距离相等,中心与一边的两个端点可以确定一个圆,正方形有四条边,因而有四个圆;而正方形的四个顶点都在以中心为圆心的圆上,因而能确定5个不同的圆.
三.解答题
21.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
22.解:(1)根据题意,图形W为以O为圆心,OA为直径的圆.
如图1,连接OD,
∴OA=OD.
∵点C为OA的中点,CD⊥AB,
∴AD=OD.
∴OA=OD=AD.
∴△OAD 是等边三角形.
∴∠AOD=60°.
∴∠ABD=30°.
(2)如图2,
∵∠ADE=∠ABD,
∴∠ADE=30°.
∵∠ADO=60°.
∴∠ODE=90°.
∴OD⊥DE.
∴DE是⊙O的切线.
∴直线DE与图形W的公共点个数为1.
23.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
24.解:由题意可知AB=2.5m,AC=1.5m,
小狗在地平面上环绕跑圆的半径为=2.0(m),
小狗活动的区域是以2.0m为半径的圆,如图.
25.解:(1)连接OB.
∵OD过圆心,且D是弦BC中点,
∴OD⊥BC,BD=BC,
在Rt△BOD中,OD2+BD2=BO2.
∵BO=AO=8,BD=6.
∴OD=2;
(2)在Rt△EOD中,OD2+ED2=EO2.
设BE=x,则OE=x,DE=6﹣x.
(2)2+(6﹣x)2=(x)2,
解得x1=﹣16(舍),x2=4.
则DE=2.
26.解:连接OA、OC,
∵由题意知:AB∥CD,OE⊥AB,OF⊥CD,CD=20cm,
∴CG=CD=10cm,
在Rt△OGC中,由勾股定理得:OC2=CG2+OG2,
OC2=102+(OC﹣2)2,
解得:OC=26(cm),
则OE=26cm﹣2cm﹣2cm=22cm,
∵在Rt△OEA中,由勾股定理得:OA2=OE2+AE2,
∴262=222+AE2,
∴AE=8,
∵OE⊥AB,OE过圆心O,
∴AB=2AE=16cm.
27.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
