2.2.4.2 二次函数y=ax2+bx+c的性质之“中考10条” 课件(共23张PPT)
文档属性
| 名称 | 2.2.4.2 二次函数y=ax2+bx+c的性质之“中考10条” 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览







文档简介
(共23张PPT)
北师版九年级下册 二次函数
2.2.4(2) 二次函数y=ax2+bx+c之“中考十条”
——a,b,c取值与图象的变化关系
3.在探索过程中,让学生深刻体会“数→形,形→数”的数形结合思想的重要意义,并能在今后分析、解决问题的过程中灵活运用.
2.经历探索y=ax2+bx+c的图象特征,理解、掌握二次函数y=ax2+bx+c的 “中考10条”,并在解题中能熟练运用.(难点)
1.经历探索y=ax2+bx+c的图象特征,理解并会运用其与y=ax2的图象与性质之间的关系解题.(重点)
一、二次函数y=ax2+bx+c(a≠0)与y=ax (a≠0)的关系
1.相同点: (1)形状相同(图象都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最大(或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y随x的增大而减小;
在对称轴右侧,y随 x的增大而增大.
a<0时,开口向下,在对称轴左侧,y随x的增大而增大;
在对称轴右侧,y随 x的增大而减小 .
2.不同点: (1)位置不同.
(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和 0.
一、二次函数y=ax2+bx+c(a≠0)与y=ax (a≠0)的关系
3.联系:
一般的二次函数y=ax2+bx+c通过转变成配方式以后,图象都可以由y=ax2的图象通过“左加右减,上加下减”八字口诀来确定;
一、二次函数y=ax2+bx+c(a≠0)与y=ax (a≠0)的关系
二、二次函数y=ax2+bx+c(a≠0)的图象与性质10条
1.顶点坐标、对称轴;
2.位置、开口方向
3.增减性与最值
抛物线
>
<
小
大
左减
右增
左增
右减
左减右增
左增右减
a= ,b= .a,b ,
a= ,b= .a,b ,
开口方向
交点纵坐标
1
-2
异号
在y轴右侧
-
-
同号
在y轴左侧
左同右异
b2-4ac=-8<0
无交点
b2-4ac=24/5>0
2
0
1
左加右减
上加下减
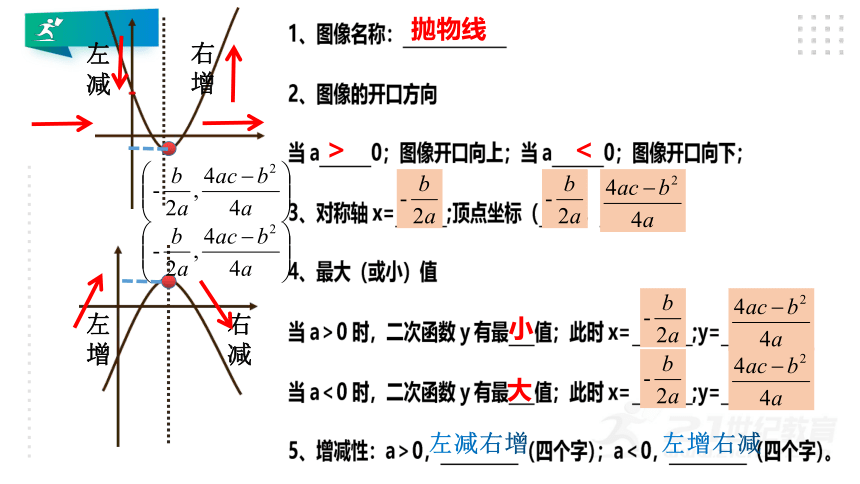
1、图像名称: ;
2、图像的开口方向
当a 0;图像开口向上;当a 0;图像开口向下;
对称轴x= ;顶点坐标( , )
最大(或小)值
当a>0时,二次函数y有最 值;此时x= ;y= ;
当a<0时,二次函数y有最 值;此时x= ;y= ;
增减性:a>0, (四个字);a<0, (四个字)。
二、二次函数y=ax2+bx+c(a≠0)的图象与性质10条
抛物线
>
<
小
大
左减右增
左增右减
a决定图像的 。
c值为图像与y轴的 。
a,b与对称轴的位置关系
当a,b同号时,对称轴在 ;
当a,b异号时,对称轴在 。
四字诀:“ ”
4.与x轴的交点个数
当b2-4ac>0时,图像与x轴有 个交点;
当b2-4ac<0时,图像与x轴有 个交点;
当b2-4ac=0时,图像与x轴有 个交点。
5.图像的平移规律
八字决:“ , ”
※注意:使用此规律时,必须把函数式配成“配方式”——
二、二次函数y=ax2+bx+c(a≠0)的图象与性质10条
开口方向
交点纵坐标
y轴左侧
y轴右侧
左同右异
2
1
0
左加右减,上加下减
观察二次函数图像的5步法解题
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
解析:
1、看开口方向:向下;∴a<0.
2、看图象与y轴的交点:c>0;
3、看对称轴的位置:由“左同右异”发现,
“a,b异号”;
4、看图象与x轴的交点个数:2个,b2-4ac>0
B
观察二次函数图像的5步法解题
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
解析:
1、看开口方向:向上;∴a>0.
2、看图象与y轴的交点:c<0;
3、看对称轴的位置:由“左同右异”发现,
“a,b同号”;
【练】(2015莱芜)二次函数 的图象如图所示,则一次函数
的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
观察二次函数图像的5步法解题
D
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
5、关于“a+b+c或a-b+c”判断
B
特别注意:a+b+c相当于
x=1, y=a+b+c
4
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
5、关于“a+b+c或a-b+c”判断
特别注意:a+b+c相当于
x=1, y=a+b+c
y=ax2+bx+c(a≠0)的图像与性质
——精编训练系列
【分析】A、二次函数的开口向下,.'.a<0,正确,不符合题意;
B、二次函数与y轴交于正半轴,..C>0,正确,不符合题意;
C、二次函数与x轴有2个交点,..b2-4ac>0,正确,不符合题意;
D、当x=1时,函数值是负数, a+b+C<0,..错误,符合题意,故选D.
【点评】考查二次函数图象与系数的关系;用到的知识点为∶二次函数的开口向下,a<0;二次函数与y轴交于正半轴,c>0;二次函数与x轴有2个交点,b2-4ac>0;a+b+c的符号用当x=1时,函数值的正负判断.
D
c
解析:
本题主要考查一次函数的图象与性质和二次函数的图象与性质。
根据一次函数的性质可得,y= bx+a的函数值y随x的增大而增大,且与y轴交点在x轴上方,
故一次函数图象经过第一、二、三象限,不经过第四象限。故本题正确答案为D。
解析∶根据二次函数的性质,开口向下,可知a<0,故①正确;
当x=1时,y>0,即a+b+c>0,故②正确;
故答案为∶①②③
本题考查了学生对二次函数的性质的理解和掌握,难度不大,比较简单,
属于基础,熟记其性质,是解答此类问题的关键所在
【分析】由抛物线开口向下知道a<0,而对称轴在y轴左侧,即b<0,因此判断①正确;由抛物线与y轴的交点在正半轴得到c>0,可以判断②正确;由图象与x轴有两个交点得到以b2-4ac>0,
因此可以判断③正确;由图象可知当x=-1时,对应的函数值y=a-b+C>0,所以判断④错.
【解答】①.'抛物线开口向下,a<0,而对称轴在y轴左侧,a、b同号,即b<0,正确∶
②∶抛物线与y轴的交点在正半轴 ,..C>0,正确;
③∶·图象与x轴有两个交点 ,.b2-4ac>0,正确;
④∶由图象可知当x=-1时,对应的函数值y=a-b+C>0,错误. 故选C.
【点评】本题考查二次函数的字母系数与图象位置之间的关系.
①④
课堂小结
3.在反复训练过程中。深刻领会了“数→形,形→数”的数形结合思想.
2.学习、领会了二次函数y=ax2+bx+c的 “中考10条”,以及解题中运用的“5步法”;
1.学习并领会了y=ax2+bx+c的图象与y=ax2的图象与性质之间的关系;
北师版九年级下册 二次函数
2.2.4(2) 二次函数y=ax2+bx+c之“中考十条”
——a,b,c取值与图象的变化关系
3.在探索过程中,让学生深刻体会“数→形,形→数”的数形结合思想的重要意义,并能在今后分析、解决问题的过程中灵活运用.
2.经历探索y=ax2+bx+c的图象特征,理解、掌握二次函数y=ax2+bx+c的 “中考10条”,并在解题中能熟练运用.(难点)
1.经历探索y=ax2+bx+c的图象特征,理解并会运用其与y=ax2的图象与性质之间的关系解题.(重点)
一、二次函数y=ax2+bx+c(a≠0)与y=ax (a≠0)的关系
1.相同点: (1)形状相同(图象都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最大(或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y随x的增大而减小;
在对称轴右侧,y随 x的增大而增大.
a<0时,开口向下,在对称轴左侧,y随x的增大而增大;
在对称轴右侧,y随 x的增大而减小 .
2.不同点: (1)位置不同.
(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和 0.
一、二次函数y=ax2+bx+c(a≠0)与y=ax (a≠0)的关系
3.联系:
一般的二次函数y=ax2+bx+c通过转变成配方式以后,图象都可以由y=ax2的图象通过“左加右减,上加下减”八字口诀来确定;
一、二次函数y=ax2+bx+c(a≠0)与y=ax (a≠0)的关系
二、二次函数y=ax2+bx+c(a≠0)的图象与性质10条
1.顶点坐标、对称轴;
2.位置、开口方向
3.增减性与最值
抛物线
>
<
小
大
左减
右增
左增
右减
左减右增
左增右减
a= ,b= .a,b ,
a= ,b= .a,b ,
开口方向
交点纵坐标
1
-2
异号
在y轴右侧
-
-
同号
在y轴左侧
左同右异
b2-4ac=-8<0
无交点
b2-4ac=24/5>0
2
0
1
左加右减
上加下减
1、图像名称: ;
2、图像的开口方向
当a 0;图像开口向上;当a 0;图像开口向下;
对称轴x= ;顶点坐标( , )
最大(或小)值
当a>0时,二次函数y有最 值;此时x= ;y= ;
当a<0时,二次函数y有最 值;此时x= ;y= ;
增减性:a>0, (四个字);a<0, (四个字)。
二、二次函数y=ax2+bx+c(a≠0)的图象与性质10条
抛物线
>
<
小
大
左减右增
左增右减
a决定图像的 。
c值为图像与y轴的 。
a,b与对称轴的位置关系
当a,b同号时,对称轴在 ;
当a,b异号时,对称轴在 。
四字诀:“ ”
4.与x轴的交点个数
当b2-4ac>0时,图像与x轴有 个交点;
当b2-4ac<0时,图像与x轴有 个交点;
当b2-4ac=0时,图像与x轴有 个交点。
5.图像的平移规律
八字决:“ , ”
※注意:使用此规律时,必须把函数式配成“配方式”——
二、二次函数y=ax2+bx+c(a≠0)的图象与性质10条
开口方向
交点纵坐标
y轴左侧
y轴右侧
左同右异
2
1
0
左加右减,上加下减
观察二次函数图像的5步法解题
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
解析:
1、看开口方向:向下;∴a<0.
2、看图象与y轴的交点:c>0;
3、看对称轴的位置:由“左同右异”发现,
“a,b异号”;
4、看图象与x轴的交点个数:2个,b2-4ac>0
B
观察二次函数图像的5步法解题
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
解析:
1、看开口方向:向上;∴a>0.
2、看图象与y轴的交点:c<0;
3、看对称轴的位置:由“左同右异”发现,
“a,b同号”;
【练】(2015莱芜)二次函数 的图象如图所示,则一次函数
的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
观察二次函数图像的5步法解题
D
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
5、关于“a+b+c或a-b+c”判断
B
特别注意:a+b+c相当于
x=1, y=a+b+c
4
1、看开口方向;
2、看与y轴的交点;
3、看对称轴的位置;
4、看与x轴的交点个数.
5、关于“a+b+c或a-b+c”判断
特别注意:a+b+c相当于
x=1, y=a+b+c
y=ax2+bx+c(a≠0)的图像与性质
——精编训练系列
【分析】A、二次函数的开口向下,.'.a<0,正确,不符合题意;
B、二次函数与y轴交于正半轴,..C>0,正确,不符合题意;
C、二次函数与x轴有2个交点,..b2-4ac>0,正确,不符合题意;
D、当x=1时,函数值是负数, a+b+C<0,..错误,符合题意,故选D.
【点评】考查二次函数图象与系数的关系;用到的知识点为∶二次函数的开口向下,a<0;二次函数与y轴交于正半轴,c>0;二次函数与x轴有2个交点,b2-4ac>0;a+b+c的符号用当x=1时,函数值的正负判断.
D
c
解析:
本题主要考查一次函数的图象与性质和二次函数的图象与性质。
根据一次函数的性质可得,y= bx+a的函数值y随x的增大而增大,且与y轴交点在x轴上方,
故一次函数图象经过第一、二、三象限,不经过第四象限。故本题正确答案为D。
解析∶根据二次函数的性质,开口向下,可知a<0,故①正确;
当x=1时,y>0,即a+b+c>0,故②正确;
故答案为∶①②③
本题考查了学生对二次函数的性质的理解和掌握,难度不大,比较简单,
属于基础,熟记其性质,是解答此类问题的关键所在
【分析】由抛物线开口向下知道a<0,而对称轴在y轴左侧,即b<0,因此判断①正确;由抛物线与y轴的交点在正半轴得到c>0,可以判断②正确;由图象与x轴有两个交点得到以b2-4ac>0,
因此可以判断③正确;由图象可知当x=-1时,对应的函数值y=a-b+C>0,所以判断④错.
【解答】①.'抛物线开口向下,a<0,而对称轴在y轴左侧,a、b同号,即b<0,正确∶
②∶抛物线与y轴的交点在正半轴 ,..C>0,正确;
③∶·图象与x轴有两个交点 ,.b2-4ac>0,正确;
④∶由图象可知当x=-1时,对应的函数值y=a-b+C>0,错误. 故选C.
【点评】本题考查二次函数的字母系数与图象位置之间的关系.
①④
课堂小结
3.在反复训练过程中。深刻领会了“数→形,形→数”的数形结合思想.
2.学习、领会了二次函数y=ax2+bx+c的 “中考10条”,以及解题中运用的“5步法”;
1.学习并领会了y=ax2+bx+c的图象与y=ax2的图象与性质之间的关系;
