数学必修二-1.2.1-2《空间几何体的三视图》
文档属性
| 名称 | 数学必修二-1.2.1-2《空间几何体的三视图》 |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-20 09:12:59 | ||
图片预览






文档简介
(共47张PPT)
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
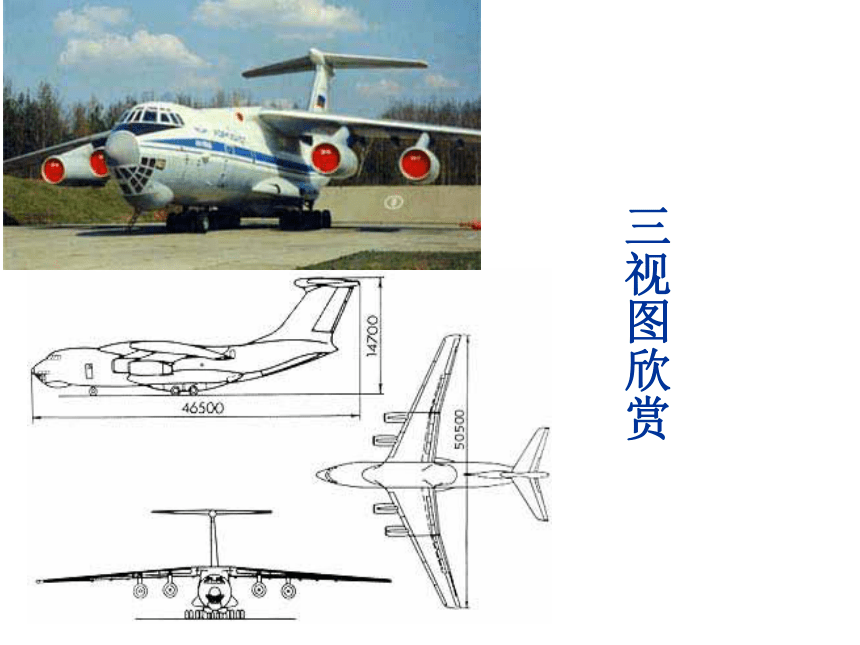
三视图欣赏
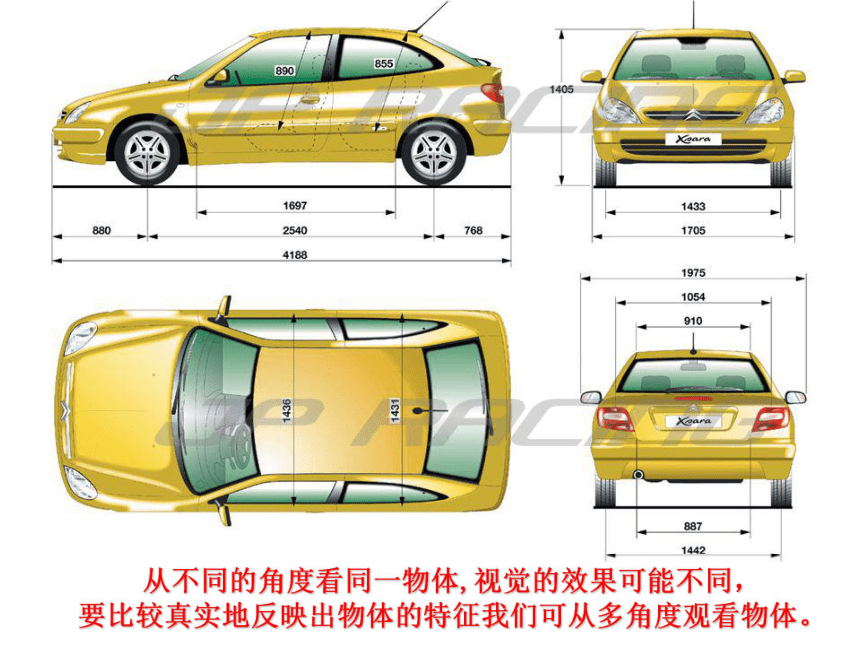
从不同的角度看同一物体,视觉的效果可能不同,
要比较真实地反映出物体的特征我们可从多角度观看物体。
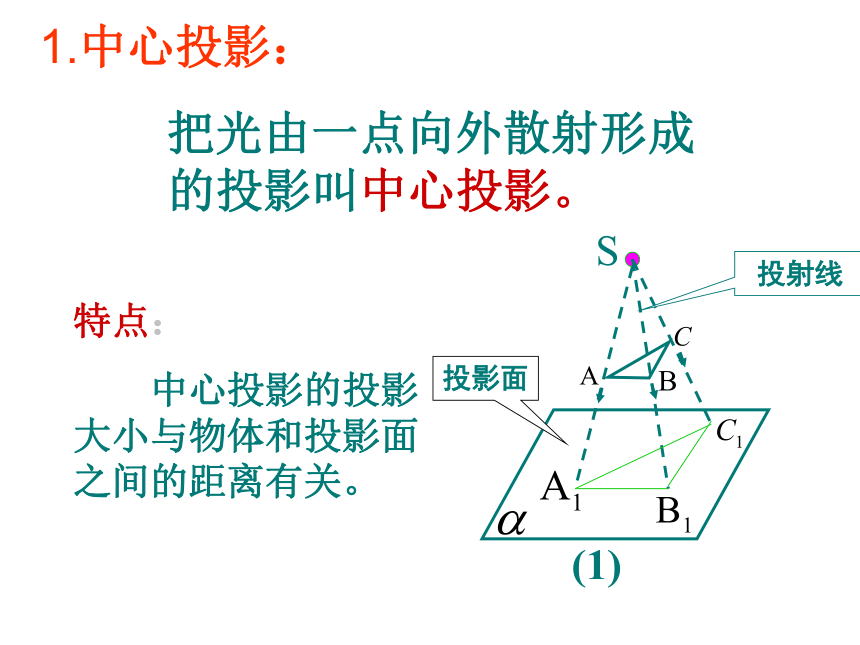
特点:
中心投影的投影大小与物体和投影面之间的距离有关。
1.中心投影:
S
(1)
把光由一点向外散射形成的投影叫中心投影。
投射线
投影面
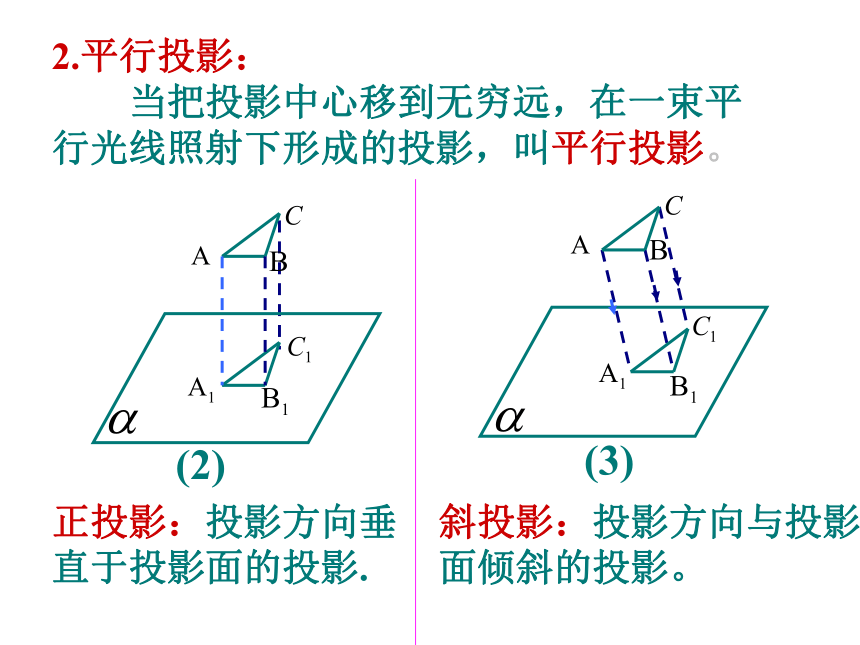
2.平行投影:
当把投影中心移到无穷远,在一束平行光线照射下形成的投影,叫平行投影。
正投影:投影方向垂直于投影面的投影.
斜投影:投影方向与投影面倾斜的投影。
(3)
(2)
特点:
与投影面平行的平面图形留下的影子, 与物体的形状大小完全相同,与物体和投影面之间的距离无关。
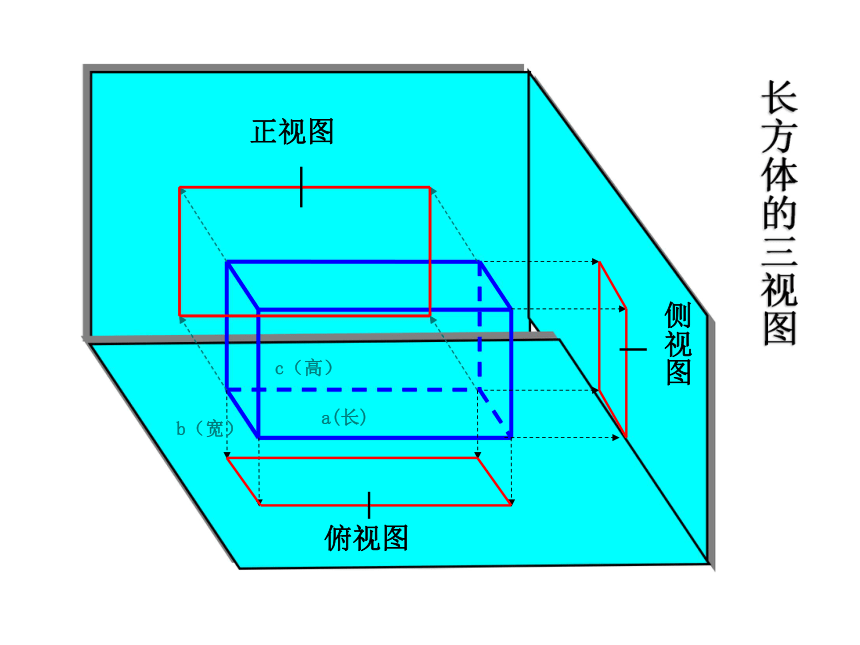
长方体的三视图
正视图
俯视图
侧视图
c(高)
a(长)
b(宽)
正视图反映了物体的高度和长度
侧视图反映了物体的高度和宽度
俯视图反映了物体的长度和宽度
c(高)
a(长)
b(宽)
正视图
侧视图
俯视图
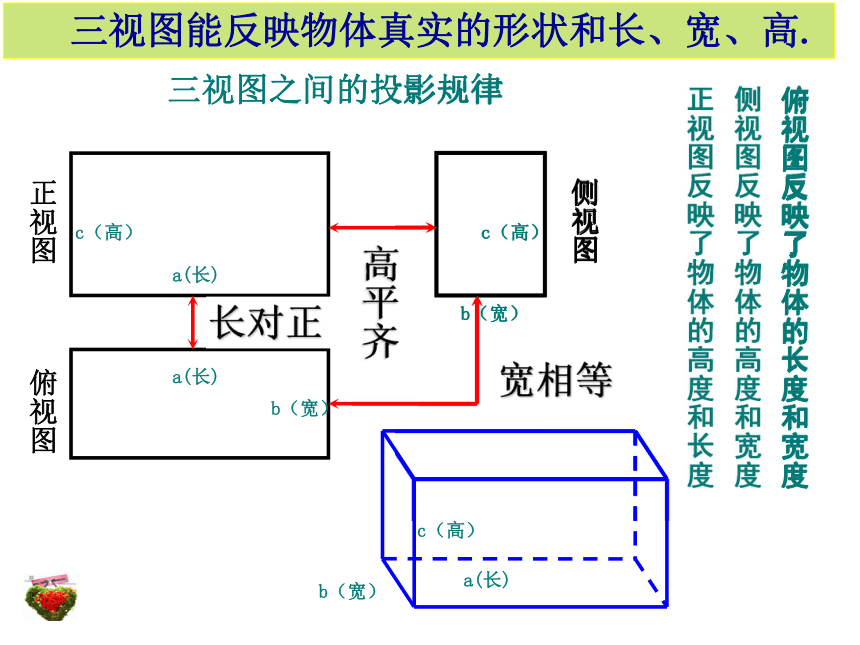
三视图之间的投影规律
a(长)
c(高)
c(高)
b(宽)
b(宽)
a(长)
长对正
高平齐
宽相等
三视图能反映物体真实的形状和长、宽、高.
圆柱
正
侧
俯
(1)圆柱的三视图
正视图
侧视图
俯视图
例1
侧
正
俯
(2)圆锥的三视图
圆 锥
例1
侧视图
正视图
俯视图
·
例2 请同学们画下面这两个圆台的三视图,如果你认为这两个圆台的三视图一样,画一个就可以;如果你认为不一样,请分别画出来。
俯视图
正视图
侧视图
俯视图
正视图
侧视图
注意:
(1)画几何体的三视图时,
能看见的轮廓和棱用实线表示,
不能看见的轮廓和棱用虚线表示。
(2)长对正, 高平齐, 宽相等。
练习、画下例几何体的三视图
侧
正
俯
除了会画如正方体、长方体、圆柱、圆锥、球
等基本几何体的三视图外,我们还将学习画出由
一些简单几何体组成的组合体的三视图。
请同学们试试画出立白洗洁精塑料瓶的三视图
正视图
侧视图
俯视图
练习:
(1)
(2)
圆柱
正视图
侧视图
俯视图
俯
侧
正
正视图
侧视图
侧视图
例3:如图所示,将一个长方体截去一部分,这个几何体的三视图是什么?
正视
正视图
侧视图
俯视图
例4、画下例几何体的三视图
例5、画下例几何体的三视图
还原成实物图:
刚才所作的三视图,
你能将其还原成实物模型吗?
圆 台
圆台
根据三视图判断几何体
正
侧
俯
俯视图
正视图
侧视图
例6
侧视图
正视图
俯视图
正视图
侧视图
俯视图
正
侧
俯
根据三视图判断几何体
例7
根据三视图判断几何体
正视图
侧视图
俯视图
例8
正
俯
侧
四棱柱
三棱柱
侧视图
俯视图
正视图
练习2
侧视图
俯视图
正视图
练习5 说出下面的三视图表示的几何体的结构特征.
正视图
侧视图
俯视图
思考2:下列两图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并作适当描述.
正视图
侧视图
俯视图
正视图
侧视图
俯视图
【三视图的画法要求】
(1)在画三视图时,重叠的线只画一条,挡住的线要画成虚线,尺寸线用细实线标出.
(2)三视图的主视图、左视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.画三视图的基本要求是:主俯一样长,俯左一样宽,主左一样高.
由三视图想象几何体特征时要根据“长对正、宽相等、高平齐”的原则作出判断.
【方法技巧提炼】
1.画三视图时,应牢记其要求的“长对正、高平齐、宽相等”,注意虚、实线的区别,同时应熟悉一些常见几何体的三视图.解决由三视图想象几何体,进而进行有关计算的题目,关键是准确把握三视图和几何体之间的关系.
2.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征,熟练掌握三视图的投影方向及正视图原理,才能迅速破解三视图问题,由三视图画出其直观图.
正视图
侧视图
探究(1): 在例6中,若只给出正,侧视图,
那么它除了是圆台外,还可能是什么几何体?
俯视图
不同的几何体可能有某一两个视图相同
所以我们只有通过全部三个视图才能
全面准确的反映一个几何体的特征。
正四棱台
俯
侧
正
探究(2):如图是一个简单组合体的三视图,想象它表示的组合体的结构特征,尝试画出它的示意图。
正视图
侧视图
俯视图
小结:
画几何体的三视图时,能看得见的轮廓线
或棱用实线表示,不能看得见的轮廓线
或棱用虚线表示。
三视图之间的投影规律:
正视图与俯视图------长对正。
正视图与侧视图------高平齐。
俯视图与侧视图------宽相等。
1、
2、
3 空间想象能力,逆向思维能力
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
三视图欣赏
从不同的角度看同一物体,视觉的效果可能不同,
要比较真实地反映出物体的特征我们可从多角度观看物体。
特点:
中心投影的投影大小与物体和投影面之间的距离有关。
1.中心投影:
S
(1)
把光由一点向外散射形成的投影叫中心投影。
投射线
投影面
2.平行投影:
当把投影中心移到无穷远,在一束平行光线照射下形成的投影,叫平行投影。
正投影:投影方向垂直于投影面的投影.
斜投影:投影方向与投影面倾斜的投影。
(3)
(2)
特点:
与投影面平行的平面图形留下的影子, 与物体的形状大小完全相同,与物体和投影面之间的距离无关。
长方体的三视图
正视图
俯视图
侧视图
c(高)
a(长)
b(宽)
正视图反映了物体的高度和长度
侧视图反映了物体的高度和宽度
俯视图反映了物体的长度和宽度
c(高)
a(长)
b(宽)
正视图
侧视图
俯视图
三视图之间的投影规律
a(长)
c(高)
c(高)
b(宽)
b(宽)
a(长)
长对正
高平齐
宽相等
三视图能反映物体真实的形状和长、宽、高.
圆柱
正
侧
俯
(1)圆柱的三视图
正视图
侧视图
俯视图
例1
侧
正
俯
(2)圆锥的三视图
圆 锥
例1
侧视图
正视图
俯视图
·
例2 请同学们画下面这两个圆台的三视图,如果你认为这两个圆台的三视图一样,画一个就可以;如果你认为不一样,请分别画出来。
俯视图
正视图
侧视图
俯视图
正视图
侧视图
注意:
(1)画几何体的三视图时,
能看见的轮廓和棱用实线表示,
不能看见的轮廓和棱用虚线表示。
(2)长对正, 高平齐, 宽相等。
练习、画下例几何体的三视图
侧
正
俯
除了会画如正方体、长方体、圆柱、圆锥、球
等基本几何体的三视图外,我们还将学习画出由
一些简单几何体组成的组合体的三视图。
请同学们试试画出立白洗洁精塑料瓶的三视图
正视图
侧视图
俯视图
练习:
(1)
(2)
圆柱
正视图
侧视图
俯视图
俯
侧
正
正视图
侧视图
侧视图
例3:如图所示,将一个长方体截去一部分,这个几何体的三视图是什么?
正视
正视图
侧视图
俯视图
例4、画下例几何体的三视图
例5、画下例几何体的三视图
还原成实物图:
刚才所作的三视图,
你能将其还原成实物模型吗?
圆 台
圆台
根据三视图判断几何体
正
侧
俯
俯视图
正视图
侧视图
例6
侧视图
正视图
俯视图
正视图
侧视图
俯视图
正
侧
俯
根据三视图判断几何体
例7
根据三视图判断几何体
正视图
侧视图
俯视图
例8
正
俯
侧
四棱柱
三棱柱
侧视图
俯视图
正视图
练习2
侧视图
俯视图
正视图
练习5 说出下面的三视图表示的几何体的结构特征.
正视图
侧视图
俯视图
思考2:下列两图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并作适当描述.
正视图
侧视图
俯视图
正视图
侧视图
俯视图
【三视图的画法要求】
(1)在画三视图时,重叠的线只画一条,挡住的线要画成虚线,尺寸线用细实线标出.
(2)三视图的主视图、左视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.画三视图的基本要求是:主俯一样长,俯左一样宽,主左一样高.
由三视图想象几何体特征时要根据“长对正、宽相等、高平齐”的原则作出判断.
【方法技巧提炼】
1.画三视图时,应牢记其要求的“长对正、高平齐、宽相等”,注意虚、实线的区别,同时应熟悉一些常见几何体的三视图.解决由三视图想象几何体,进而进行有关计算的题目,关键是准确把握三视图和几何体之间的关系.
2.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征,熟练掌握三视图的投影方向及正视图原理,才能迅速破解三视图问题,由三视图画出其直观图.
正视图
侧视图
探究(1): 在例6中,若只给出正,侧视图,
那么它除了是圆台外,还可能是什么几何体?
俯视图
不同的几何体可能有某一两个视图相同
所以我们只有通过全部三个视图才能
全面准确的反映一个几何体的特征。
正四棱台
俯
侧
正
探究(2):如图是一个简单组合体的三视图,想象它表示的组合体的结构特征,尝试画出它的示意图。
正视图
侧视图
俯视图
小结:
画几何体的三视图时,能看得见的轮廓线
或棱用实线表示,不能看得见的轮廓线
或棱用虚线表示。
三视图之间的投影规律:
正视图与俯视图------长对正。
正视图与侧视图------高平齐。
俯视图与侧视图------宽相等。
1、
2、
3 空间想象能力,逆向思维能力
