2021-2022学年湘教新版八年级上册数学《第3章 实数》单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教新版八年级上册数学《第3章 实数》单元测试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 00:00:00 | ||
图片预览



文档简介
2021-2022学年湘教新版八年级上册数学《第3章 实数》单元测试卷
一.选择题
1.的平方根是( )
A.9 B.3 C.±9 D.±3
2.16平方根是( )
A.4 B.﹣4 C.±4 D.±8
3.a2=16,则a是( )
A.4或﹣4 B.﹣4 C.4 D.8或﹣8
4.实数9的算术平方根是( )
A.3 B.﹣3 C.±3 D.81
5.用科学计算器计算:(﹣6.192)×100等于( )
A.4434.730995 B.﹣3786.832774
C.﹣1826.61 D.646.11263545
6.下列实数是无理数的是( )
A.3.14 B. C. D.
7.下列各数中的无理数是( )
A. B.0. C.﹣ D.
8.下列说法正确的是( )
A.0.01的平方根是0.1 B.=4
C.0的立方根是0 D.1的立方根是±1
9.下列说法不正确的是( )
A.的平方根是± B.﹣9是81的平方根
C.0.4的算术平方根是0.2 D.=﹣3
10.若+|a﹣4|=0,则化简的结果是( )
A. B.± C. D.±
二.填空题
11.请写出两个你熟悉的无理数: .
12.已知一个正数的两个平方根分别是2m﹣6和3+m,则m的值为 .
13.64的平方根是 .
14.的算术平方根是 .
15.若(a﹣3)2+=0,则= .
16.计算:= .
17.一个正数的平方根分别为2x+1和x﹣7,则这个正数为 .
18.(1)2005年11月1日零时,全国总人口为130 628万人,60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示约为 万人(用计算器计算,保留3位有效数字).
(2)用计算器比较大小: 0(填“>“、“=“、“<“).
19.若5x+19的立方根是4,则2x+7的平方根是 .
20.在、、﹣π中, 是无理数.
三.解答题
21.求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如,但可以通过计算器求.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n 16 0.16 0.0016 1600 160000 …
4 x 0.04 y 400 …
(1)表格中x= ;y= ;
(2)从表格中探究n与数位的规律,并利用这个规律解决下面两个问题:
①已知≈1.435,则≈ ;
②已知=1.83,若=0.183,则x= .
22.求下列各式中的x
(1)4x2=81;
(2)(2x+10)3=﹣27.
23.已知 2(x+1)2﹣49=1,求x的值.
24.如图是一块正方形纸片.
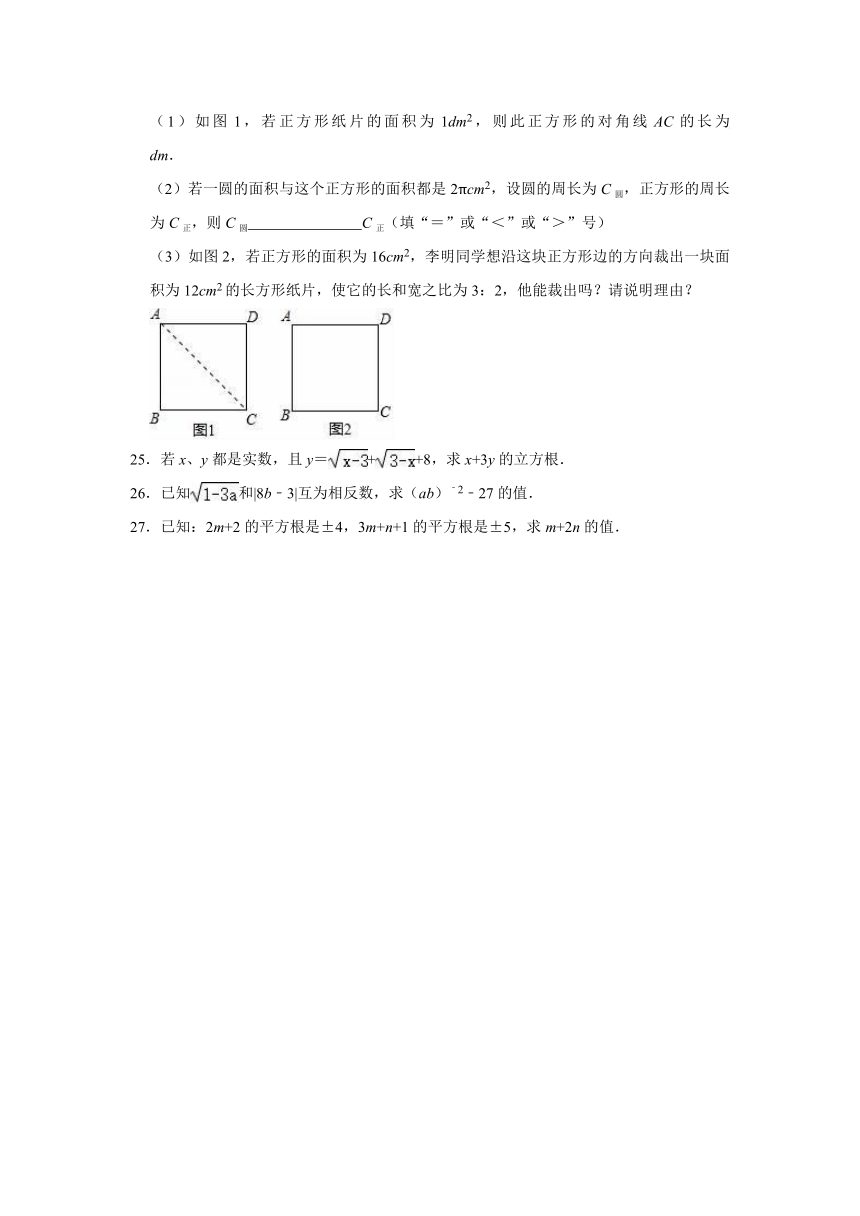
(1)如图1,若正方形纸片的面积为1dm2,则此正方形的对角线AC的长为 dm.
(2)若一圆的面积与这个正方形的面积都是2πcm2,设圆的周长为C圆,正方形的周长为C正,则C圆 C正(填“=”或“<”或“>”号)
(3)如图2,若正方形的面积为16cm2,李明同学想沿这块正方形边的方向裁出一块面积为12cm2的长方形纸片,使它的长和宽之比为3:2,他能裁出吗?请说明理由?
25.若x、y都是实数,且y=++8,求x+3y的立方根.
26.已知和|8b﹣3|互为相反数,求(ab)﹣2﹣27的值.
27.已知:2m+2的平方根是±4,3m+n+1的平方根是±5,求m+2n的值.
参考答案与试题解析
一.选择题
1.解:因为=9,
所以9的平方根是±3,
故选:D.
2.解:16平方根是±4.
故选:C.
3.解:16的平方根为±4.
故选:A.
4.解:∵32=9,
∴9算术平方根为3.
故选:A.
5.解:(﹣6.192)×100=646.11263545.
故选:D.
6.解:A.3.14是有限小数,属于有理数;
B.是分数,属于有理数;
C.是无理数;
D.,是整数,属于有理数.
故选:C.
7.解:A、是分数,是有理数,选项错误;
B、是无限循环小数,是有理数,选项错误;
C、正确;
D、=2是整数,是有理数,选项错误.
故选:C.
8.解:A、0.01的平方根是±0.1,所以A选项错误;
B、=4,所以B选项错误;
C、0的立方根为0,所以C选项正确;
D、1的立方根为1,所以D选项错误.
故选:C.
9.解:0.4的算术平方根为,故C错误,
故选:C.
10.解:∵ +|a﹣4|=0,
∴b﹣3=0,a﹣4=0,
∴b=3,a=4,
∴==.
故选:A.
二.填空题
11.解:无理数是:π,0.1010010001….
12.解:由题意可知:(2m﹣6)+(3+m)=0,
∴m=1,
故答案为:1.
13.解:∵(±8)2=64,
∴64的平方根是±8.
故答案为:±8.
14.解:的算术平方根是,故答案为.
15.解:∵(a﹣3)2+=0,
∴a﹣3=0,b﹣1=0,
解得:a=3,b=1,
==2.
故答案为:2.
16.解:=﹣3.
故答案为:﹣3.
17.解:∵一个正数的平方根是2x+1和x﹣7,
∴2x+1+x﹣7=0,
解得:x=2,
故2x+1=5,
则这个正数是:52=25.
故答案为:25.
18.解:(1)130628×11.03%≈1.44×104;
(2)∵≈2.571,≈2.449,
∴>0.
故填空答案:(1)1.44×104;(2)>.
19.解:∵5x+19的立方根是4,
∴5x+19=64,
解得x=9
则2x+7=2×9+7=25,
∴25的平方根是±5
故答案±5.
20.解:=0.3,=3,
∴无理数有﹣π,
故答案为:﹣π.
三.解答题
21.解:(1)根据题意得,x=0.4,y=40;
故答案为:0.4,40;
(2)①已知≈1.435,则≈143.5;
故答案为:143.5;
②已知=1.83,若=0.183,则x=0.03489.
故答案为:0.03489.
22.(1)解:∵x2=,
∴x=±=±;
(2)解:2x+10=,
∴2x+10=﹣3,
∴x=﹣.
23.解:∵2(x+1)2﹣49=1,
∴2(x+1)2=50,(x+1)2=25.
∴x+1=±5.
∴x=4或x=﹣6.
24.(1)解:由已知AB2=1,则AB=1,
由勾股定理,AC=;
或根据AC2=1,可得AC=,
故答案为:
(2)由圆面积公式,
可得圆半径为,周长为,
正方形周长为4.
;
故答案为:<
(3)不能;
由已知设长方形长和宽为3xcm和2xcm
∴长方形面积为:2x 3x=12
∴解得x=
∴长方形长边为3>4
∴他不能裁出.
25.解:∵y=++8,
∴
解得:x=3,
将x=3代入原式,得到y=8,
∴x+3y=3+3×8=27,
∴=3,
即x+3y的立方根为3.
26.解:∵和|8b﹣3|互为相反数,
∴+|8b﹣3|=0,
∴1﹣3a=0,8b﹣3=0,
解得a=,b=,
∴(ab)﹣2﹣27=(×)﹣2﹣27,
=()﹣2﹣27,
=64﹣27,
=37.
27.解:∵2m+2的平方根是±4,3m+n+1的平方根是±5,
∴2m+2=16,3m+n+1=25,
联立解得,m=7,n=3,
∴m+2n=7+2×3=13.
故答案为:13.
一.选择题
1.的平方根是( )
A.9 B.3 C.±9 D.±3
2.16平方根是( )
A.4 B.﹣4 C.±4 D.±8
3.a2=16,则a是( )
A.4或﹣4 B.﹣4 C.4 D.8或﹣8
4.实数9的算术平方根是( )
A.3 B.﹣3 C.±3 D.81
5.用科学计算器计算:(﹣6.192)×100等于( )
A.4434.730995 B.﹣3786.832774
C.﹣1826.61 D.646.11263545
6.下列实数是无理数的是( )
A.3.14 B. C. D.
7.下列各数中的无理数是( )
A. B.0. C.﹣ D.
8.下列说法正确的是( )
A.0.01的平方根是0.1 B.=4
C.0的立方根是0 D.1的立方根是±1
9.下列说法不正确的是( )
A.的平方根是± B.﹣9是81的平方根
C.0.4的算术平方根是0.2 D.=﹣3
10.若+|a﹣4|=0,则化简的结果是( )
A. B.± C. D.±
二.填空题
11.请写出两个你熟悉的无理数: .
12.已知一个正数的两个平方根分别是2m﹣6和3+m,则m的值为 .
13.64的平方根是 .
14.的算术平方根是 .
15.若(a﹣3)2+=0,则= .
16.计算:= .
17.一个正数的平方根分别为2x+1和x﹣7,则这个正数为 .
18.(1)2005年11月1日零时,全国总人口为130 628万人,60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示约为 万人(用计算器计算,保留3位有效数字).
(2)用计算器比较大小: 0(填“>“、“=“、“<“).
19.若5x+19的立方根是4,则2x+7的平方根是 .
20.在、、﹣π中, 是无理数.
三.解答题
21.求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如,但可以通过计算器求.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n 16 0.16 0.0016 1600 160000 …
4 x 0.04 y 400 …
(1)表格中x= ;y= ;
(2)从表格中探究n与数位的规律,并利用这个规律解决下面两个问题:
①已知≈1.435,则≈ ;
②已知=1.83,若=0.183,则x= .
22.求下列各式中的x
(1)4x2=81;
(2)(2x+10)3=﹣27.
23.已知 2(x+1)2﹣49=1,求x的值.
24.如图是一块正方形纸片.
(1)如图1,若正方形纸片的面积为1dm2,则此正方形的对角线AC的长为 dm.
(2)若一圆的面积与这个正方形的面积都是2πcm2,设圆的周长为C圆,正方形的周长为C正,则C圆 C正(填“=”或“<”或“>”号)
(3)如图2,若正方形的面积为16cm2,李明同学想沿这块正方形边的方向裁出一块面积为12cm2的长方形纸片,使它的长和宽之比为3:2,他能裁出吗?请说明理由?
25.若x、y都是实数,且y=++8,求x+3y的立方根.
26.已知和|8b﹣3|互为相反数,求(ab)﹣2﹣27的值.
27.已知:2m+2的平方根是±4,3m+n+1的平方根是±5,求m+2n的值.
参考答案与试题解析
一.选择题
1.解:因为=9,
所以9的平方根是±3,
故选:D.
2.解:16平方根是±4.
故选:C.
3.解:16的平方根为±4.
故选:A.
4.解:∵32=9,
∴9算术平方根为3.
故选:A.
5.解:(﹣6.192)×100=646.11263545.
故选:D.
6.解:A.3.14是有限小数,属于有理数;
B.是分数,属于有理数;
C.是无理数;
D.,是整数,属于有理数.
故选:C.
7.解:A、是分数,是有理数,选项错误;
B、是无限循环小数,是有理数,选项错误;
C、正确;
D、=2是整数,是有理数,选项错误.
故选:C.
8.解:A、0.01的平方根是±0.1,所以A选项错误;
B、=4,所以B选项错误;
C、0的立方根为0,所以C选项正确;
D、1的立方根为1,所以D选项错误.
故选:C.
9.解:0.4的算术平方根为,故C错误,
故选:C.
10.解:∵ +|a﹣4|=0,
∴b﹣3=0,a﹣4=0,
∴b=3,a=4,
∴==.
故选:A.
二.填空题
11.解:无理数是:π,0.1010010001….
12.解:由题意可知:(2m﹣6)+(3+m)=0,
∴m=1,
故答案为:1.
13.解:∵(±8)2=64,
∴64的平方根是±8.
故答案为:±8.
14.解:的算术平方根是,故答案为.
15.解:∵(a﹣3)2+=0,
∴a﹣3=0,b﹣1=0,
解得:a=3,b=1,
==2.
故答案为:2.
16.解:=﹣3.
故答案为:﹣3.
17.解:∵一个正数的平方根是2x+1和x﹣7,
∴2x+1+x﹣7=0,
解得:x=2,
故2x+1=5,
则这个正数是:52=25.
故答案为:25.
18.解:(1)130628×11.03%≈1.44×104;
(2)∵≈2.571,≈2.449,
∴>0.
故填空答案:(1)1.44×104;(2)>.
19.解:∵5x+19的立方根是4,
∴5x+19=64,
解得x=9
则2x+7=2×9+7=25,
∴25的平方根是±5
故答案±5.
20.解:=0.3,=3,
∴无理数有﹣π,
故答案为:﹣π.
三.解答题
21.解:(1)根据题意得,x=0.4,y=40;
故答案为:0.4,40;
(2)①已知≈1.435,则≈143.5;
故答案为:143.5;
②已知=1.83,若=0.183,则x=0.03489.
故答案为:0.03489.
22.(1)解:∵x2=,
∴x=±=±;
(2)解:2x+10=,
∴2x+10=﹣3,
∴x=﹣.
23.解:∵2(x+1)2﹣49=1,
∴2(x+1)2=50,(x+1)2=25.
∴x+1=±5.
∴x=4或x=﹣6.
24.(1)解:由已知AB2=1,则AB=1,
由勾股定理,AC=;
或根据AC2=1,可得AC=,
故答案为:
(2)由圆面积公式,
可得圆半径为,周长为,
正方形周长为4.
;
故答案为:<
(3)不能;
由已知设长方形长和宽为3xcm和2xcm
∴长方形面积为:2x 3x=12
∴解得x=
∴长方形长边为3>4
∴他不能裁出.
25.解:∵y=++8,
∴
解得:x=3,
将x=3代入原式,得到y=8,
∴x+3y=3+3×8=27,
∴=3,
即x+3y的立方根为3.
26.解:∵和|8b﹣3|互为相反数,
∴+|8b﹣3|=0,
∴1﹣3a=0,8b﹣3=0,
解得a=,b=,
∴(ab)﹣2﹣27=(×)﹣2﹣27,
=()﹣2﹣27,
=64﹣27,
=37.
27.解:∵2m+2的平方根是±4,3m+n+1的平方根是±5,
∴2m+2=16,3m+n+1=25,
联立解得,m=7,n=3,
∴m+2n=7+2×3=13.
故答案为:13.
同课章节目录
