函数y=Asin(ωx φ)的图象
图片预览





文档简介
(共23张PPT)
函数 y=Asin( x+ ) 的图象(二)
1.5 函数y=Asin(ωx+φ)的图象
目的:
1.这种函数在物理学和工程学中应用比较广泛;
2.通过y=Asin(ωx+φ)的图象及性质的研究,能 举一反三地掌其他三角函数的图象及其性质。
能用五点法或通过变换y=sinx的图象作出函数y=Asin(ωx+φ)
的图象,了解y=Asin(ωx+φ)的性质及其与y=sinx 的图象关系。
重点、难点:
当函数y=Asin(ωx+φ),(A>0,ω>0),x ∈[0,+∞)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做这个振动的振幅;往复振动一次所需要的时间T=2π/ω,它叫做振动的周期;单位时间内往复振动的次数f=1/T=ω/2π,它叫做振动的频率;ωx+φ叫做相位,φ叫做初相(即当x=0时的相).
一、复习回顾
1、函数y=Asin(ωx+φ)中A、ω、φ的物理意义
2、上一节课我们学习了三角函数图象哪几种的变换?
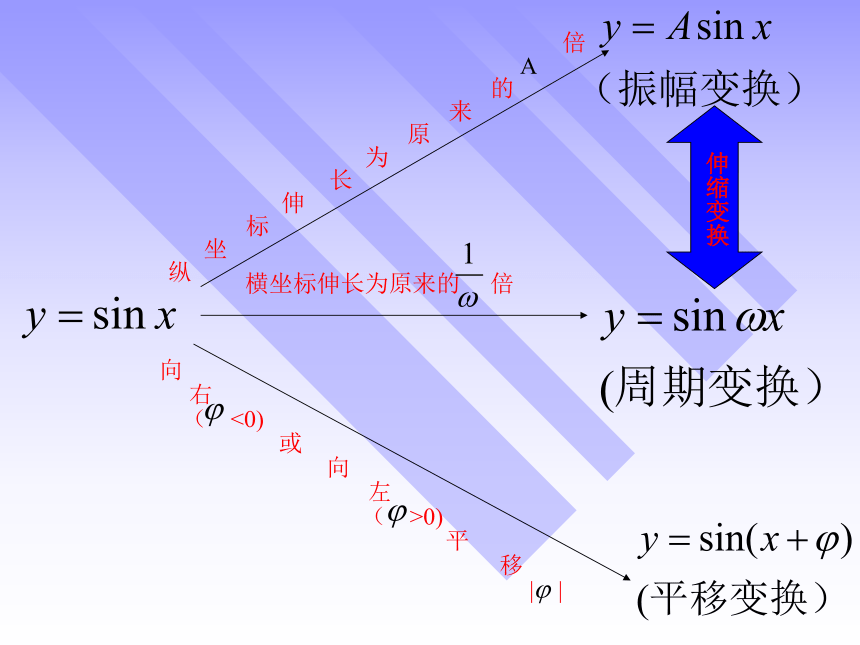
振幅变换
y=Asinx
y=sinx
y=sinx
y=sinx
周期变换
相位(左右)变换
y=sinωx
y=Asin(x+φ)
伸缩变换
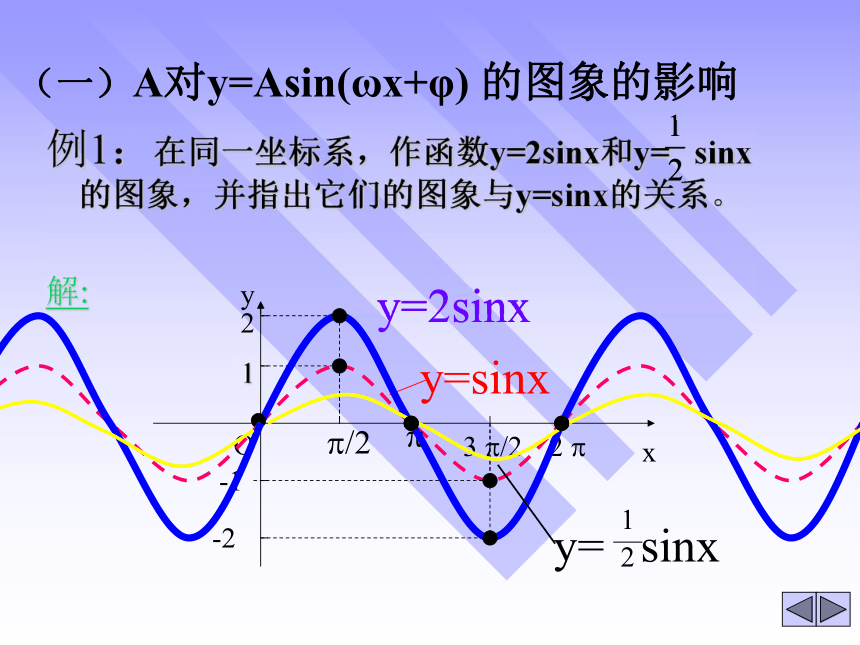
(一)A对y=Asin(ωx+φ) 的图象的影响
例1:在同一坐标系,作函数y=2sinx和y= sinx的图象,并指出它们的图象与y=sinx的关系。
解:
y=2sinx
y=sinx
O
/2
3 /2
2
-1
-2
x
1
y
2
1
—
2
y= sinx
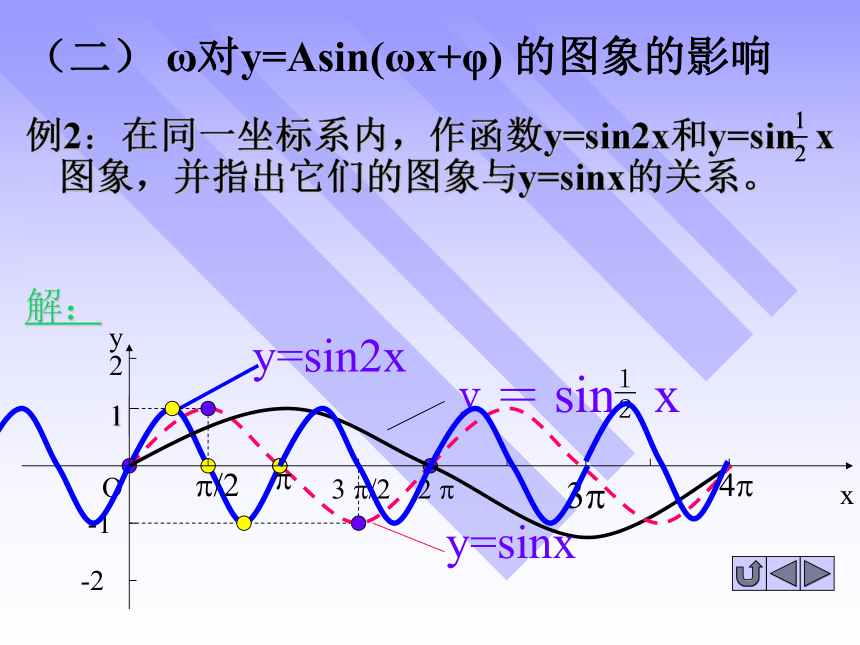
例2:在同一坐标系内,作函数y=sin2x和y=sin x图象,并指出它们的图象与y=sinx的关系。
解:
(二) ω对y=Asin(ωx+φ) 的图象的影响
y=sin2x
O
/2
3 /2
2
-1
-2
x
1
y
2
3
4
y= sin x
1
-2
y=sinx
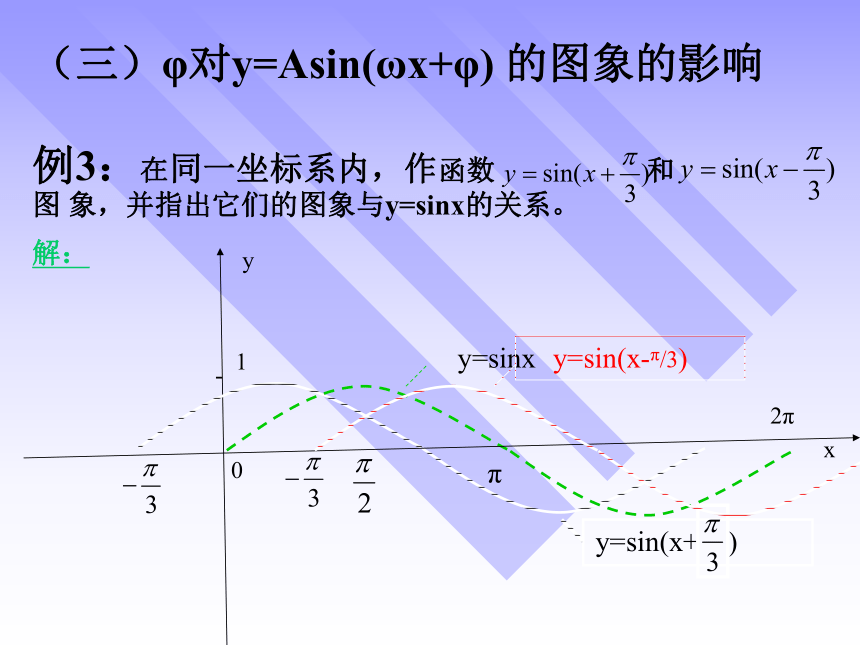
例3:在同一坐标系内,作函数 和 图 象,并指出它们的图象与y=sinx的关系。
解:
(三)φ对y=Asin(ωx+φ) 的图象的影响
y=sin(x+ )
x
y
1
-
0
y=sinx
y=sin(x-π/3)
π
2π
横坐标伸长为原来的 倍
倍
A
的
来
原
为
长
伸
标
坐
纵
向
右
( <0)
或
向
左
( >0)
平
移
| |
伸缩变换
函数y=Asin(ωx+φ),(A>0,ω>0)的图象
与y=sinx的图象有什么关系呢?
能不能由y=sinx的图象变换得函数y=Asin(ωx+φ)的图象呢?
下面我们通过两种方法作出函数y=Asin(ω+φ) 的图象
二、活动与探究
例1 作函数 y = 3sin(2 + )的简图
分析 :
因为T= ,所以用“五点法”先作长度为一个周期的闭区间上的简图
设
则
当 X =0,
, , , 时,可求得相对应的 、y 的
值,得到“五点”,再描点作图 。然后将简图左右扩展。
一. 五点法
y=3sin(2x+ )
略解:
(2) 描点:
(3)连线:
(4)根据周期性将作出的简图左右扩展。
0
0
0
0
3
3
2
(1)列表:
x
y
o
3
-3
作函数 的简图,并指出它与y=sinx图象的关系。
解法一: 先平移后伸缩
解法二:先伸缩后平移
思考:对y=sinx的图象经过怎样的移动可以得到上题中函数图象?
二、图象变换
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sinx
y=sin(x+ )①
y=3sin(2x+ )③
方法1:先平移后伸缩演示
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sinx
y=3sin(2x+ )③
y=sin2x①
方法2:先伸缩后平移演示1
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=3sin(2x+ )③
y=3sinx①
y=3sin2x②
先伸缩后平移演示2
向左平移 个单位,再将所得图象上所有点
的横坐标变为原来的 倍(纵坐标不变)
向左平移 个单位,再将所得图象上所有点
向右平移 个单位
的纵坐标变为原来的 倍(横坐标不变)
(2). 为了得到函数 的图象,只需把C上的
1.已知函数 图象为C
(1).为了得到函数 的图象,只需把C上的
所有点
所有点
所有点
(3). 为了得到函数 的图象,只需把C上的
.求函数 的周期并作其图象
解法一: 先平移后伸缩
解法二:先伸缩后平移
向左平移 个单位
再将图象上的所有点的横坐标变为原来的 倍
2.把函数 的图象向右平移 个单位,
所得图象的函数解析式为
(纵坐标不变),则所得图象函数解析式为
3.要得到函数 的图象,只需将函数
的图象
4.函数 振幅、周期、初相各是多少?
答案略(学生自己完成)
1.对于函数 y=Asin( x+ ) (A>0, >0):
A --- 振幅,
--- 周期,
--- 频率,
x+ --- 相位,
--- 初相.
2.图象的变换:
(1)伸缩变换
振幅变换
周期变换
(2)平移变换
上下平移
左右平移
( ----- 形状变换)
( ----- 位置变换)
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
或:
y=sin x
横坐标变为原来的 倍
纵坐标不变
1
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
向左( >0)或向右( <0)
平移 个单位
y=sin (x+ )
=sin( x+ )
书本P45第7、8题
函数 y=Asin( x+ ) 的图象(二)
1.5 函数y=Asin(ωx+φ)的图象
目的:
1.这种函数在物理学和工程学中应用比较广泛;
2.通过y=Asin(ωx+φ)的图象及性质的研究,能 举一反三地掌其他三角函数的图象及其性质。
能用五点法或通过变换y=sinx的图象作出函数y=Asin(ωx+φ)
的图象,了解y=Asin(ωx+φ)的性质及其与y=sinx 的图象关系。
重点、难点:
当函数y=Asin(ωx+φ),(A>0,ω>0),x ∈[0,+∞)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做这个振动的振幅;往复振动一次所需要的时间T=2π/ω,它叫做振动的周期;单位时间内往复振动的次数f=1/T=ω/2π,它叫做振动的频率;ωx+φ叫做相位,φ叫做初相(即当x=0时的相).
一、复习回顾
1、函数y=Asin(ωx+φ)中A、ω、φ的物理意义
2、上一节课我们学习了三角函数图象哪几种的变换?
振幅变换
y=Asinx
y=sinx
y=sinx
y=sinx
周期变换
相位(左右)变换
y=sinωx
y=Asin(x+φ)
伸缩变换
(一)A对y=Asin(ωx+φ) 的图象的影响
例1:在同一坐标系,作函数y=2sinx和y= sinx的图象,并指出它们的图象与y=sinx的关系。
解:
y=2sinx
y=sinx
O
/2
3 /2
2
-1
-2
x
1
y
2
1
—
2
y= sinx
例2:在同一坐标系内,作函数y=sin2x和y=sin x图象,并指出它们的图象与y=sinx的关系。
解:
(二) ω对y=Asin(ωx+φ) 的图象的影响
y=sin2x
O
/2
3 /2
2
-1
-2
x
1
y
2
3
4
y= sin x
1
-2
y=sinx
例3:在同一坐标系内,作函数 和 图 象,并指出它们的图象与y=sinx的关系。
解:
(三)φ对y=Asin(ωx+φ) 的图象的影响
y=sin(x+ )
x
y
1
-
0
y=sinx
y=sin(x-π/3)
π
2π
横坐标伸长为原来的 倍
倍
A
的
来
原
为
长
伸
标
坐
纵
向
右
( <0)
或
向
左
( >0)
平
移
| |
伸缩变换
函数y=Asin(ωx+φ),(A>0,ω>0)的图象
与y=sinx的图象有什么关系呢?
能不能由y=sinx的图象变换得函数y=Asin(ωx+φ)的图象呢?
下面我们通过两种方法作出函数y=Asin(ω+φ) 的图象
二、活动与探究
例1 作函数 y = 3sin(2 + )的简图
分析 :
因为T= ,所以用“五点法”先作长度为一个周期的闭区间上的简图
设
则
当 X =0,
, , , 时,可求得相对应的 、y 的
值,得到“五点”,再描点作图 。然后将简图左右扩展。
一. 五点法
y=3sin(2x+ )
略解:
(2) 描点:
(3)连线:
(4)根据周期性将作出的简图左右扩展。
0
0
0
0
3
3
2
(1)列表:
x
y
o
3
-3
作函数 的简图,并指出它与y=sinx图象的关系。
解法一: 先平移后伸缩
解法二:先伸缩后平移
思考:对y=sinx的图象经过怎样的移动可以得到上题中函数图象?
二、图象变换
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sinx
y=sin(x+ )①
y=3sin(2x+ )③
方法1:先平移后伸缩演示
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sinx
y=3sin(2x+ )③
y=sin2x①
方法2:先伸缩后平移演示1
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=3sin(2x+ )③
y=3sinx①
y=3sin2x②
先伸缩后平移演示2
向左平移 个单位,再将所得图象上所有点
的横坐标变为原来的 倍(纵坐标不变)
向左平移 个单位,再将所得图象上所有点
向右平移 个单位
的纵坐标变为原来的 倍(横坐标不变)
(2). 为了得到函数 的图象,只需把C上的
1.已知函数 图象为C
(1).为了得到函数 的图象,只需把C上的
所有点
所有点
所有点
(3). 为了得到函数 的图象,只需把C上的
.求函数 的周期并作其图象
解法一: 先平移后伸缩
解法二:先伸缩后平移
向左平移 个单位
再将图象上的所有点的横坐标变为原来的 倍
2.把函数 的图象向右平移 个单位,
所得图象的函数解析式为
(纵坐标不变),则所得图象函数解析式为
3.要得到函数 的图象,只需将函数
的图象
4.函数 振幅、周期、初相各是多少?
答案略(学生自己完成)
1.对于函数 y=Asin( x+ ) (A>0, >0):
A --- 振幅,
--- 周期,
--- 频率,
x+ --- 相位,
--- 初相.
2.图象的变换:
(1)伸缩变换
振幅变换
周期变换
(2)平移变换
上下平移
左右平移
( ----- 形状变换)
( ----- 位置变换)
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
或:
y=sin x
横坐标变为原来的 倍
纵坐标不变
1
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
向左( >0)或向右( <0)
平移 个单位
y=sin (x+ )
=sin( x+ )
书本P45第7、8题
