数学必修二-1.3.1《柱体、锥体和台体的表面积>>
文档属性
| 名称 | 数学必修二-1.3.1《柱体、锥体和台体的表面积>> |  | |
| 格式 | zip | ||
| 文件大小 | 554.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-20 09:20:41 | ||
图片预览



文档简介
(共24张PPT)
1.3.1《柱体、
锥体和台体的表面积》
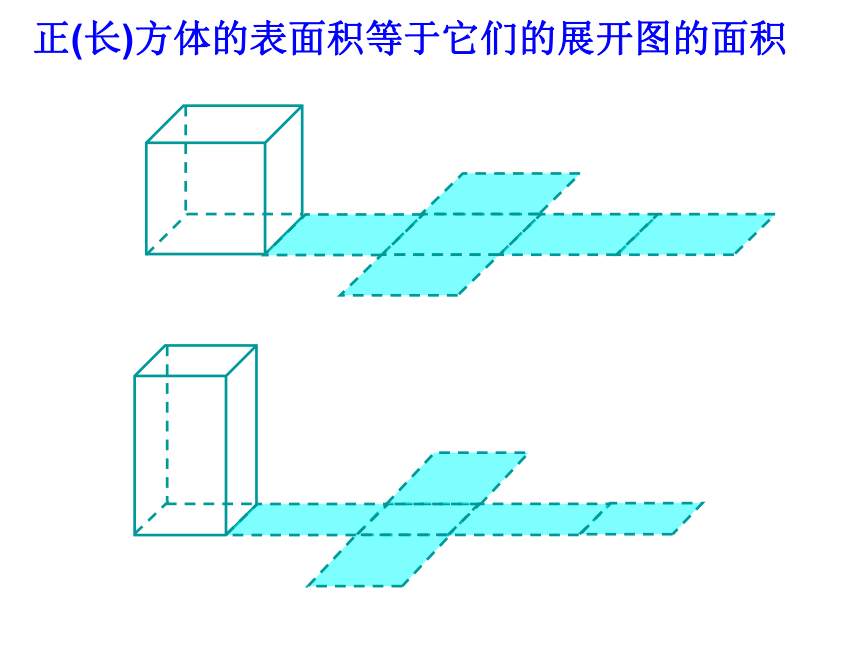
正(长)方体的表面积等于它们的展开图的面积
提出问题:柱体,锥体,台体的侧面展开图是怎样的?你能否计算?
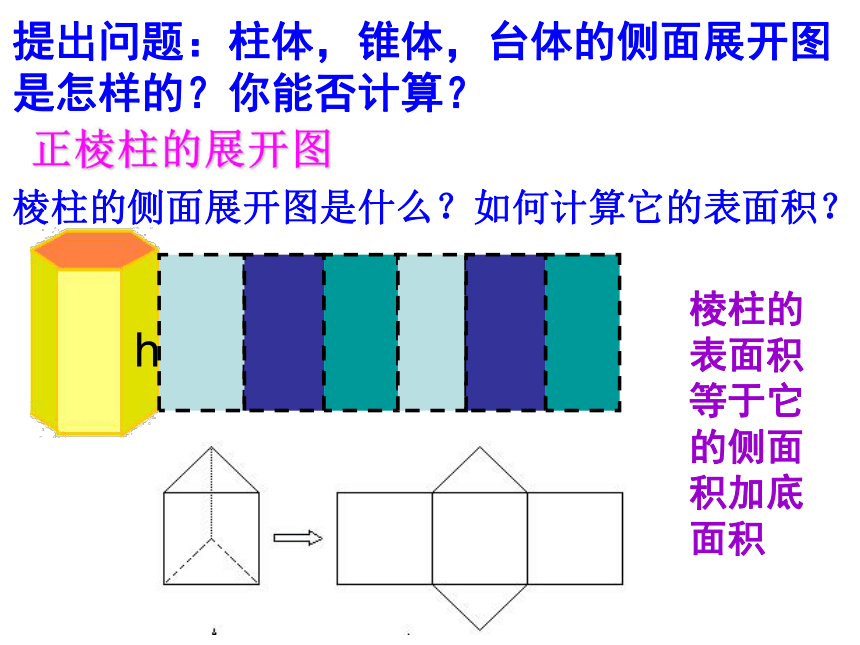
正棱柱的展开图
棱柱的侧面展开图是什么?如何计算它的表面积?
h
棱柱的
表面积
等于它
的侧面
积加底
面积
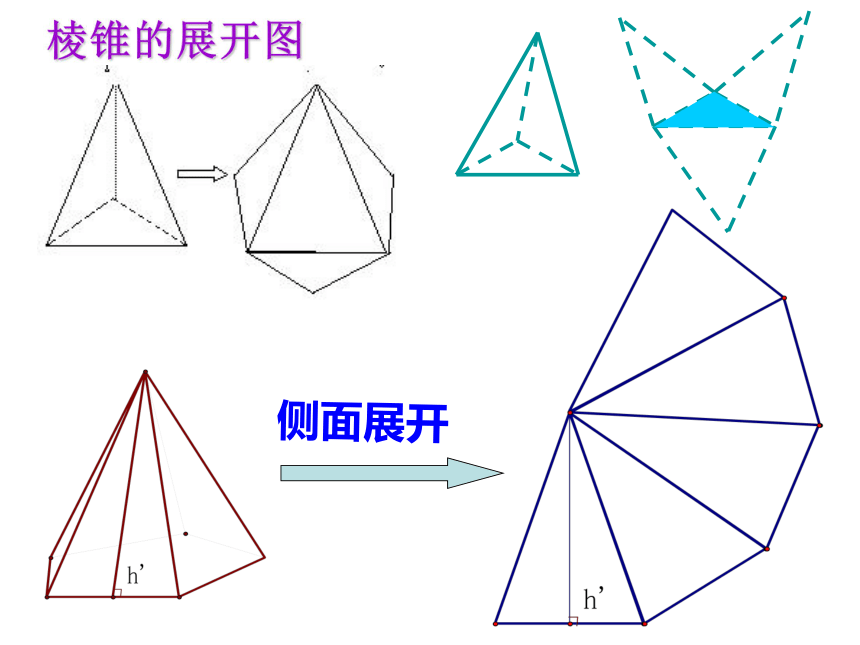
棱锥的展开图
侧面展开
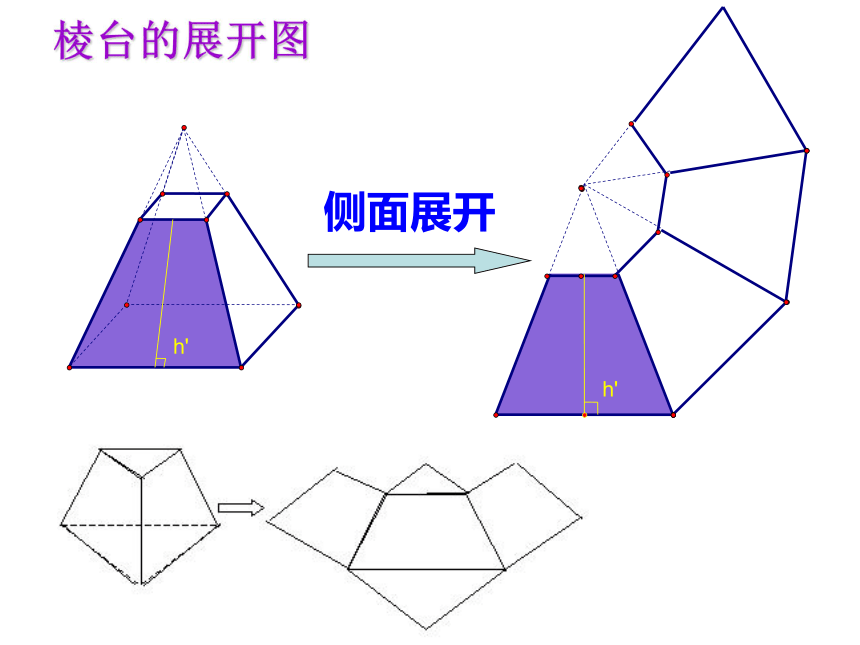
棱台的展开图
h'
h'
侧面展开
棱柱的侧面展开图是由平行四边形组成的平面图形,棱锥的侧面展开图是由三角形组成的平面图形,棱台的侧面展开图是由梯形组成的平面图形。
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。
例1:已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积.
分析:四面体的表面积等于其中任何一个面面积的4倍。
S
B
A
C
解:先求△SBC的面积,过点S作SD⊥BC,交BC于点D.
因为BC=a,
所以:
因此,四面体的表面积
D
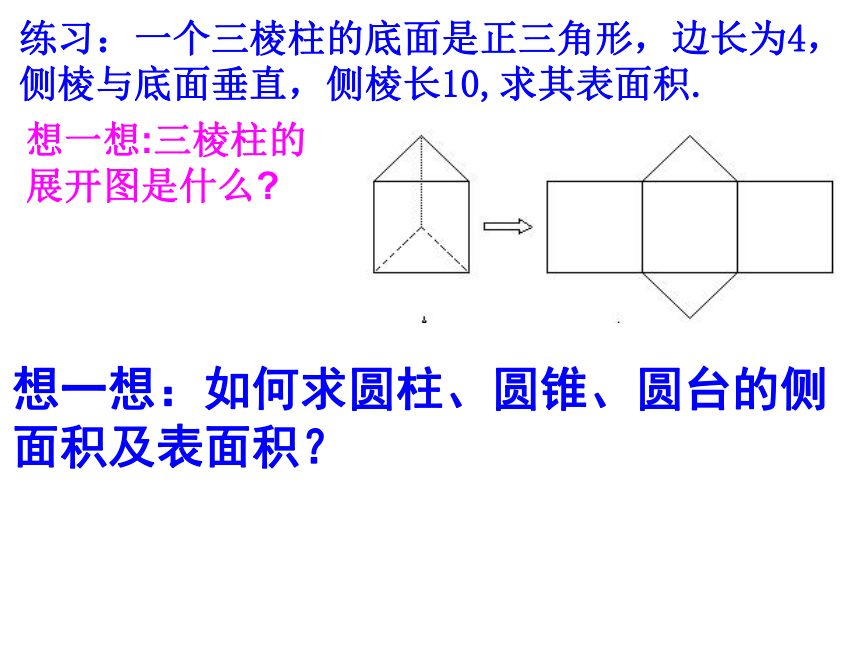
练习:一个三棱柱的底面是正三角形,边长为4,侧棱与底面垂直,侧棱长10,求其表面积.
想一想:如何求圆柱、圆锥、圆台的侧面积及表面积?
想一想:三棱柱的
展开图是什么
O
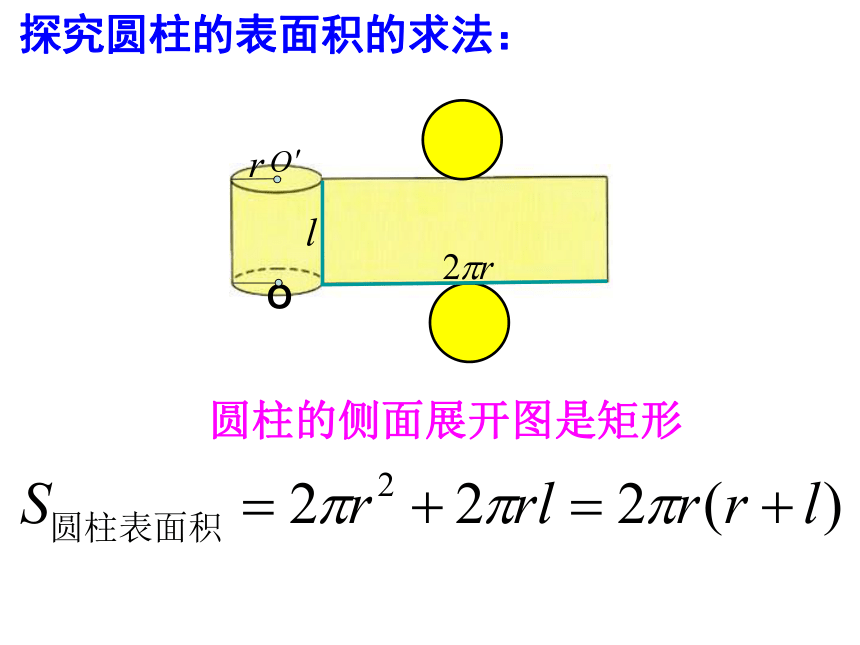
圆柱的侧面展开图是矩形
探究圆柱的表面积的求法:
圆锥的侧面展开图是扇形
O
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 .
O
O’
圆台的侧面展开图是扇环
探究圆台的表面积的求法:
练一练:一个圆台,上、下底面半径分别为10、20,母线与底面的夹角为60°,求圆台的表面积.
O`
O
变式:想一想,你能求出切割之前的圆锥的表面积吗 试试看!
思考:圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
O
O’
O
O
圆柱、圆锥、圆台三者的表面积公式之间的关系。
r’=r
上底扩大
r’=0
上底缩小
示范例题
例2:(见P25)一圆台形花盆,盆口直径20cm,盆底直径15cm,底部渗水圆孔直径1.5cm,盆壁长15cm.. 为美化外表而涂油漆,若每平方米用100毫升油漆,涂100个这样的花盘要多少油漆?
(π取3.14,结果精确到1毫升)
分析、思考:油漆位置在什么地方?→ 如何求花盆外壁表面积?
解:如图,由圆台的表面积公式得一个花盆外壁的表面积
涂100个这样的花盘需油漆:0.1×100×100=1000(毫升).
答:涂100个这样的花盘需油漆1000毫升.
变式训练:若内外涂,涂100个这样的花盘需要多少油漆
圆柱
圆锥
圆台
展
开
图
表面 积
公式
1.3.1《柱体、 锥体和台体的体积》
探究新知:
回顾:还记得特殊的棱柱—正方体、长方体,以及圆柱的体积计算公式吗?
正方体、长方体,以及圆柱的体积公式可以统一为:
V = Sh(S为底面面积,h为高)
1、探究柱体的体积公式
结论:等底、等高的棱柱、圆柱的体积相等.
归纳:一般柱体的体积 V=Sh,
其中S为底面面积,h为柱体的高。
2、探究锥体的体积公式
结论1 :等底面积等高的两个锥体的体积相等。
结论2:三棱锥的体积等于它的底面积乘以高的积的三分之一。
锥体的体积计算公式:
S为底面面积,h为高。
讨论:台体的上底面积S’,下底面积S,高h,由此如何计算切割前的锥体的高?
→ 如何计算台体的体积?
解:设切割前的小锥体的高为x,
则:
高h
下底面积S
上底面积S′
例1(P26) 有一堆规格相同的铁制(铁的密度是
7.8g/cm3)六角螺帽共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14)
分析、讨论:六角螺帽的几何结构特征怎样? → 如何求其体积? → 利用哪些数量关系求螺帽的个数?
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:
所以螺帽的个数为
5.8×1000÷(7.8×2.956)
≈252(个)
答:这堆螺帽大约有252个.
1.3.1《柱体、
锥体和台体的表面积》
正(长)方体的表面积等于它们的展开图的面积
提出问题:柱体,锥体,台体的侧面展开图是怎样的?你能否计算?
正棱柱的展开图
棱柱的侧面展开图是什么?如何计算它的表面积?
h
棱柱的
表面积
等于它
的侧面
积加底
面积
棱锥的展开图
侧面展开
棱台的展开图
h'
h'
侧面展开
棱柱的侧面展开图是由平行四边形组成的平面图形,棱锥的侧面展开图是由三角形组成的平面图形,棱台的侧面展开图是由梯形组成的平面图形。
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。
例1:已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积.
分析:四面体的表面积等于其中任何一个面面积的4倍。
S
B
A
C
解:先求△SBC的面积,过点S作SD⊥BC,交BC于点D.
因为BC=a,
所以:
因此,四面体的表面积
D
练习:一个三棱柱的底面是正三角形,边长为4,侧棱与底面垂直,侧棱长10,求其表面积.
想一想:如何求圆柱、圆锥、圆台的侧面积及表面积?
想一想:三棱柱的
展开图是什么
O
圆柱的侧面展开图是矩形
探究圆柱的表面积的求法:
圆锥的侧面展开图是扇形
O
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 .
O
O’
圆台的侧面展开图是扇环
探究圆台的表面积的求法:
练一练:一个圆台,上、下底面半径分别为10、20,母线与底面的夹角为60°,求圆台的表面积.
O`
O
变式:想一想,你能求出切割之前的圆锥的表面积吗 试试看!
思考:圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
O
O’
O
O
圆柱、圆锥、圆台三者的表面积公式之间的关系。
r’=r
上底扩大
r’=0
上底缩小
示范例题
例2:(见P25)一圆台形花盆,盆口直径20cm,盆底直径15cm,底部渗水圆孔直径1.5cm,盆壁长15cm.. 为美化外表而涂油漆,若每平方米用100毫升油漆,涂100个这样的花盘要多少油漆?
(π取3.14,结果精确到1毫升)
分析、思考:油漆位置在什么地方?→ 如何求花盆外壁表面积?
解:如图,由圆台的表面积公式得一个花盆外壁的表面积
涂100个这样的花盘需油漆:0.1×100×100=1000(毫升).
答:涂100个这样的花盘需油漆1000毫升.
变式训练:若内外涂,涂100个这样的花盘需要多少油漆
圆柱
圆锥
圆台
展
开
图
表面 积
公式
1.3.1《柱体、 锥体和台体的体积》
探究新知:
回顾:还记得特殊的棱柱—正方体、长方体,以及圆柱的体积计算公式吗?
正方体、长方体,以及圆柱的体积公式可以统一为:
V = Sh(S为底面面积,h为高)
1、探究柱体的体积公式
结论:等底、等高的棱柱、圆柱的体积相等.
归纳:一般柱体的体积 V=Sh,
其中S为底面面积,h为柱体的高。
2、探究锥体的体积公式
结论1 :等底面积等高的两个锥体的体积相等。
结论2:三棱锥的体积等于它的底面积乘以高的积的三分之一。
锥体的体积计算公式:
S为底面面积,h为高。
讨论:台体的上底面积S’,下底面积S,高h,由此如何计算切割前的锥体的高?
→ 如何计算台体的体积?
解:设切割前的小锥体的高为x,
则:
高h
下底面积S
上底面积S′
例1(P26) 有一堆规格相同的铁制(铁的密度是
7.8g/cm3)六角螺帽共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14)
分析、讨论:六角螺帽的几何结构特征怎样? → 如何求其体积? → 利用哪些数量关系求螺帽的个数?
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:
所以螺帽的个数为
5.8×1000÷(7.8×2.956)
≈252(个)
答:这堆螺帽大约有252个.
