2021-2022学年青岛新版九年级上册数学《第3章 对圆的进一步认识》单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛新版九年级上册数学《第3章 对圆的进一步认识》单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 430.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 07:26:56 | ||
图片预览



文档简介
2021-2022学年青岛新版九年级上册数学《第3章 对圆的进一步认识》单元测试卷
一.选择题
1.如图,⊙O的半径为5,若OP=3,则经过点P的弦长可能是( )
A.3 B.6 C.9 D.12
2.如图,⊙O的半径为5,弦心距OC=3,则弦AB的长是( )
A.4 B.6 C.8 D.5
3.如果⊙O的半径为10cm,点P到圆心的距离为8cm,则点P和⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.不能确定
4.已知⊙O的半径为2,点P到圆心O的距离为,则点P在( )
A.圆内 B.圆上 C.圆外 D.不能确定
5.如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心.如果使用此工具找到圆心,最少使用次数为( )
A.1 B.2 C.3 D.4
6.经过不在同一直线上的三个点可以作圆的个数是( )
A.1 B.2 C.3 D.无数
7.如图,⊙O的直径为10,弦AB的长为8,点P是弦AB上的一个动点,使线段OP的长度为整数的点P有( )
A.3个 B.4个 C.5个 D.6个
8.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=8,则cosB的值是( )
A. B. C. D.
9.如图,已知MN是⊙O的直径,弦AB⊥MN,垂足为C,若∠AON=30°,AB=,则CN=( )
A. B. C. D.2
10.如图,点D在半圆O上,半径OB=,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
二.填空题
11.如图所示,点A是半圆上的一个三等分点,B是劣弧的中点,点P是直径MN上的一个动点,⊙O的半径为1,则AP+PB的最小值 .
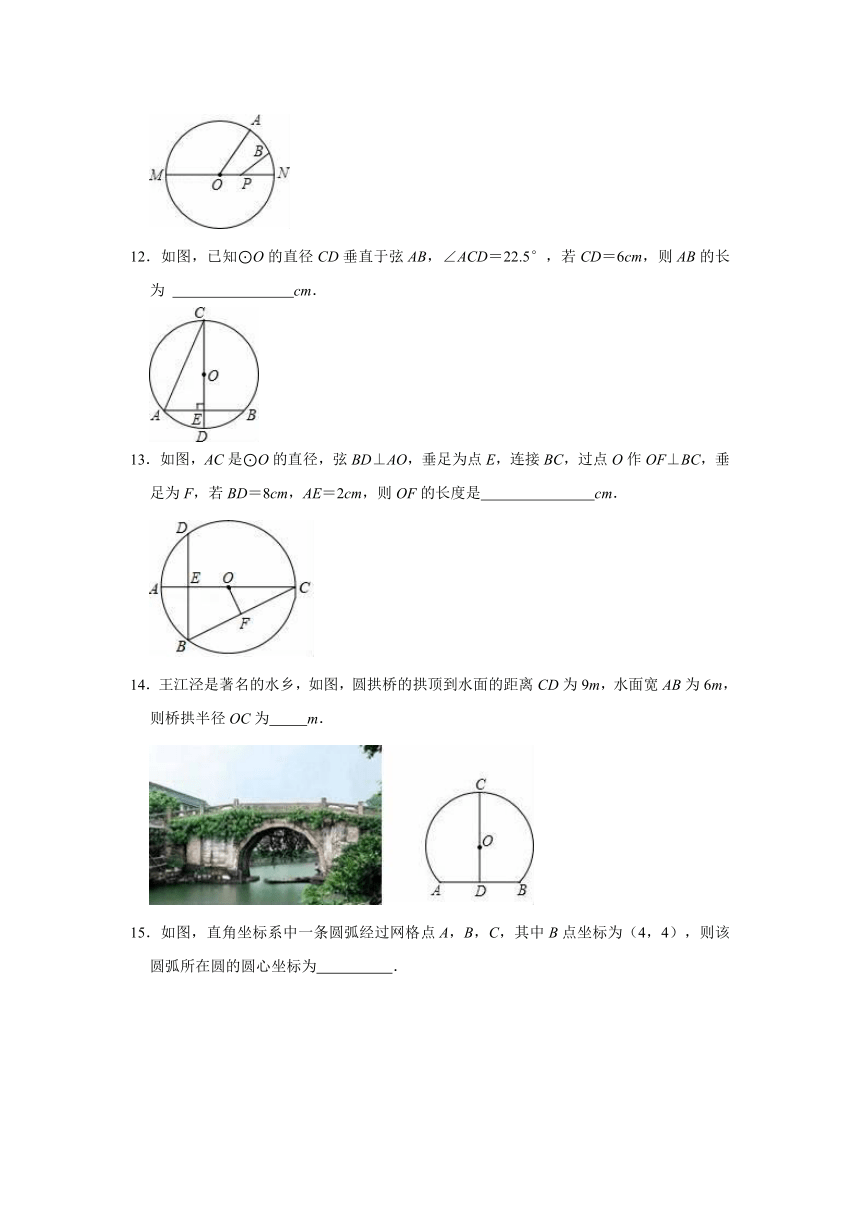
12.如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为 cm.
13.如图,AC是⊙O的直径,弦BD⊥AO,垂足为点E,连接BC,过点O作OF⊥BC,垂足为F,若BD=8cm,AE=2cm,则OF的长度是 cm.
14.王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为 m.
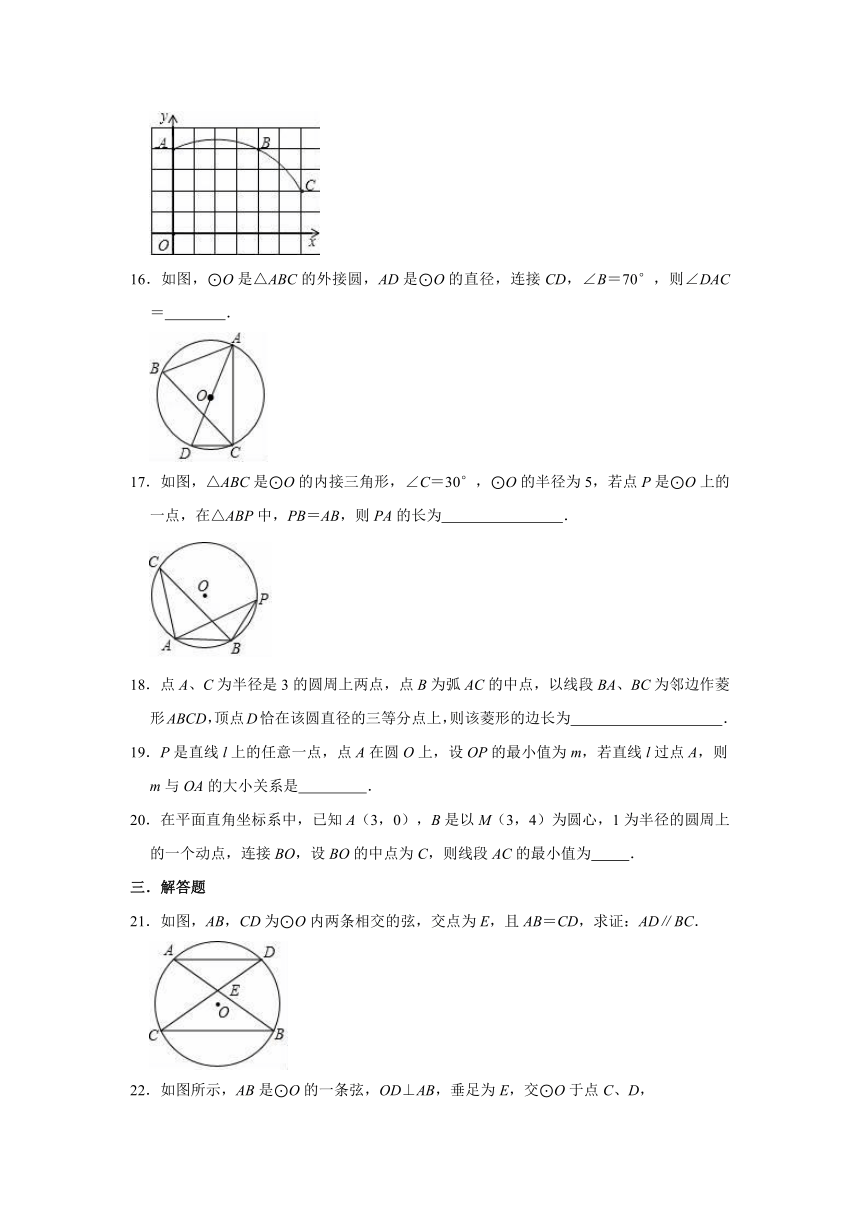
15.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .
16.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,∠B=70°,则∠DAC= .
17.如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为 .
18.点A、C为半径是3的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .
19.P是直线l上的任意一点,点A在圆O上,设OP的最小值为m,若直线l过点A,则m与OA的大小关系是 .
20.在平面直角坐标系中,已知A(3,0),B是以M(3,4)为圆心,1为半径的圆周上的一个动点,连接BO,设BO的中点为C,则线段AC的最小值为 .
三.解答题
21.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
22.如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,
(1)若∠AOD=52°,求∠DOB的度数;
(2)若AB=2,ED=1,求CD的长.
23.如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由.
24.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
25.由于过度采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近来A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向转移,如图所示,距沙尘暴中心300km的范围内将受到影响,则A市是否会受到这次沙尘暴的影响?
26.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
27.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
参考答案与试题解析
一.选择题
1.解:过P作AB⊥OP,交⊙O于A、B,连接OA;
在Rt△OAP中,OA=5,OP=3;
根据勾股定理,得:AP==4;
故AB=2AP=8;
所以过P点的弦长应该在8~10之间,
故选:C.
2.解:连接OA,如图所示,
∵OC⊥AB,OC=3,OA=5,
∴AB=2AC,
∵AC===4,
∴AB=2AC=8.
故选:C.
3.解:∵点P到圆心的距离为8cm,小于⊙O的半径10cm,
∴点P在⊙O内.故选A.
4.解:∵点P到圆心的距离,小于圆的半径2,
∴点P在圆内.
故选:A.
5.解:如图所示,
根据垂径定理的推论,两个直径的交点即为圆心.
故选:B.
6.解:经过不在同一直线上的三点确定一个圆.
故选:A.
7.解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=8,∴AP=BP=4,
在直角三角形AOP中,OA=5,AP=4,
根据勾股定理得:OP==3,即OP的最小值为3;
当P与A或B重合时,OP最长,此时OP=5,
∴3≤OP≤5,
则使线段OP的长度为整数的点P有3,4,5,共5个.
故选:C.
8.解:∵AD是⊙O的直径,
∴∠ACD=90°.
Rt△ACD中,AD=2r=10,AC=8.
根据勾股定理,得:
CD=.
∴cosD=.
∵∠B=∠D,
∴cosB=cosD=,
故选:B.
9.解:∵MN是⊙O的直径,弦AB⊥MN,∠AON=30°,AB=,
∴OA=2AC,AB=2AC,
∴OA=AB=4=ON,
∴OC=,
∴CN=ON﹣OC=4﹣6,
故选:A.
10.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
二.填空题
11.解:作点A关于MN的对称点A′,连接A′B,交MN于点P,连接OA′,OA,OB,PA,AA′.
∵点A与A′关于MN对称,点A是半圆上的一个三等分点,
∴∠A′ON=∠AON=60°,PA=PA′,
∵点B是弧AN的中点,
∴∠BON=30°,
∴∠A′OB=∠A′ON+∠BON=90°,
又∵OA=OA′=1,
∴A′B=.
∴PA+PB=PA′+PB=A′B=.
故答案为:.
12.解:连接OA,如图,
∵OA=OC,
∴∠OCA=∠CAO=22.5°,
∴∠AOD=45°,
∵CD⊥AB,
∴AE=BE,△OAE为等腰直角三角形,
而CD=6cm,
∴OA=3cm,
∴AE=OA=cm,
∴AB=2AE=3(cm).
故答案为3.
13.解:连接AB,
∵BD⊥AO,
∴BE=ED=BD=4,
由勾股定理得,AB==2,
∵OF⊥BC,
∴CF=FB,又CO=OA,
∴OF=AB=(cm),
故答案为:.
14.解:连接OA,
∵OD⊥AB,
∴AD=AB=3m,
在Rt△AOD中,OA2=OD2+AD2,即OC2=(9﹣OC)2+32,
解得,OC=5m,
故答案为:5.
15.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0).
故答案为:(2,0)
16.解:∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠D=∠B=70°,
∴∠DAC=20°,
故答案为:20°.
17.解:连接OA、OP,连接OB交AP于H,
由圆周角定理得,∠AOB=2∠C=60°,
∵PB=AB,
∴∠POB=60°,OB⊥AP,
则AH=PH=OP×sin∠POH=,
∴AP=2AH=5,
故答案为:5.
18.解:过B作直径,连接AC交BO于点E,
∵点B为的中点,
∴BD⊥AC,
如图①,
∵点D恰在该圆直径的三等分点上,
∴BD=×2×3=2,
∴OD=OB﹣BD=1,
∵四边形ABCD是菱形,
∴DE=BD=1,
∴OE=2,
连接OC,
∵CE==,
∴边CD==;
如图②,BD=×2×3=4,
同理可得,OD=1,OE=1,DE=2,
连接OC,
∵CE===2,
∴边CD===2,
故答案为或2.
19.解:因为点A在圆O上,直线l过点A,
可得:m≤OA.
故答案为:m≤OA
20.解:过B作BD∥AC交x轴于D,
∵C是OB的中点,
∴OA=AD,
∴AC=BD,
∴当BD取最小值时,AC最小,
由图可知:当BD经过M时,线段BD的长最小,此时AC有最小值,
∵A(3,0),
∴D(6,0),
∵M(3,4),
∴DM==5,
∴BD=5﹣1=4,
∴AC=BD=2,即线段AC的最小值为2;
故答案为:2.
三.解答题
21.解:∵AB=CD,
∴=,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
22.解:(1)∵OD⊥AB,
∴=,
∴∠DOB=∠AOD=52°;
(2)设半径是r,
在直角△AOE中,OE2+AE2=OA2,
则(r﹣1)2+()2=r2,
解得r=4,
则CD=2r=8.
23.解:(1)如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=AB=6m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,
解得r=6.5.
(2)∵CD=4m,船舱顶部为长方形并高出水面3.4m,
∴CE=4﹣3.4=0.6(m),
∴OE=r﹣CE=6.5﹣0.6=5.9(m),
在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣5.92=7.44,
∴EN=(m).
∴MN=2EN=2×≈5.4m>5m.
∴此货船能顺利通过这座拱桥.
24.解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).
故答案为(2,0);
(3)圆的半径AM==2.
线段MD==<2,
所以点D在⊙M内.
25.解:过A作AC⊥BD于C,由题意得AB=400km,
∠DBA=45°,所以AC=BC.
在Rt△ABC中,设AC=BC=x.
由勾股定理,得AC2+BC2=AB2,所以x2+x2=4002,
所以AC=x=200≈282.8(km).
282.8km<300km.
所以A市将受到这次沙尘暴的影响.
26.证明:过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD
27.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴,即=,
∴AE=,
∴DE=.
一.选择题
1.如图,⊙O的半径为5,若OP=3,则经过点P的弦长可能是( )
A.3 B.6 C.9 D.12
2.如图,⊙O的半径为5,弦心距OC=3,则弦AB的长是( )
A.4 B.6 C.8 D.5
3.如果⊙O的半径为10cm,点P到圆心的距离为8cm,则点P和⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.不能确定
4.已知⊙O的半径为2,点P到圆心O的距离为,则点P在( )
A.圆内 B.圆上 C.圆外 D.不能确定
5.如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心.如果使用此工具找到圆心,最少使用次数为( )
A.1 B.2 C.3 D.4
6.经过不在同一直线上的三个点可以作圆的个数是( )
A.1 B.2 C.3 D.无数
7.如图,⊙O的直径为10,弦AB的长为8,点P是弦AB上的一个动点,使线段OP的长度为整数的点P有( )
A.3个 B.4个 C.5个 D.6个
8.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=8,则cosB的值是( )
A. B. C. D.
9.如图,已知MN是⊙O的直径,弦AB⊥MN,垂足为C,若∠AON=30°,AB=,则CN=( )
A. B. C. D.2
10.如图,点D在半圆O上,半径OB=,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
二.填空题
11.如图所示,点A是半圆上的一个三等分点,B是劣弧的中点,点P是直径MN上的一个动点,⊙O的半径为1,则AP+PB的最小值 .
12.如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为 cm.
13.如图,AC是⊙O的直径,弦BD⊥AO,垂足为点E,连接BC,过点O作OF⊥BC,垂足为F,若BD=8cm,AE=2cm,则OF的长度是 cm.
14.王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为 m.
15.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .
16.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,∠B=70°,则∠DAC= .
17.如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为 .
18.点A、C为半径是3的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .
19.P是直线l上的任意一点,点A在圆O上,设OP的最小值为m,若直线l过点A,则m与OA的大小关系是 .
20.在平面直角坐标系中,已知A(3,0),B是以M(3,4)为圆心,1为半径的圆周上的一个动点,连接BO,设BO的中点为C,则线段AC的最小值为 .
三.解答题
21.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
22.如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,
(1)若∠AOD=52°,求∠DOB的度数;
(2)若AB=2,ED=1,求CD的长.
23.如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由.
24.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
25.由于过度采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近来A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向转移,如图所示,距沙尘暴中心300km的范围内将受到影响,则A市是否会受到这次沙尘暴的影响?
26.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
27.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
参考答案与试题解析
一.选择题
1.解:过P作AB⊥OP,交⊙O于A、B,连接OA;
在Rt△OAP中,OA=5,OP=3;
根据勾股定理,得:AP==4;
故AB=2AP=8;
所以过P点的弦长应该在8~10之间,
故选:C.
2.解:连接OA,如图所示,
∵OC⊥AB,OC=3,OA=5,
∴AB=2AC,
∵AC===4,
∴AB=2AC=8.
故选:C.
3.解:∵点P到圆心的距离为8cm,小于⊙O的半径10cm,
∴点P在⊙O内.故选A.
4.解:∵点P到圆心的距离,小于圆的半径2,
∴点P在圆内.
故选:A.
5.解:如图所示,
根据垂径定理的推论,两个直径的交点即为圆心.
故选:B.
6.解:经过不在同一直线上的三点确定一个圆.
故选:A.
7.解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=8,∴AP=BP=4,
在直角三角形AOP中,OA=5,AP=4,
根据勾股定理得:OP==3,即OP的最小值为3;
当P与A或B重合时,OP最长,此时OP=5,
∴3≤OP≤5,
则使线段OP的长度为整数的点P有3,4,5,共5个.
故选:C.
8.解:∵AD是⊙O的直径,
∴∠ACD=90°.
Rt△ACD中,AD=2r=10,AC=8.
根据勾股定理,得:
CD=.
∴cosD=.
∵∠B=∠D,
∴cosB=cosD=,
故选:B.
9.解:∵MN是⊙O的直径,弦AB⊥MN,∠AON=30°,AB=,
∴OA=2AC,AB=2AC,
∴OA=AB=4=ON,
∴OC=,
∴CN=ON﹣OC=4﹣6,
故选:A.
10.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
二.填空题
11.解:作点A关于MN的对称点A′,连接A′B,交MN于点P,连接OA′,OA,OB,PA,AA′.
∵点A与A′关于MN对称,点A是半圆上的一个三等分点,
∴∠A′ON=∠AON=60°,PA=PA′,
∵点B是弧AN的中点,
∴∠BON=30°,
∴∠A′OB=∠A′ON+∠BON=90°,
又∵OA=OA′=1,
∴A′B=.
∴PA+PB=PA′+PB=A′B=.
故答案为:.
12.解:连接OA,如图,
∵OA=OC,
∴∠OCA=∠CAO=22.5°,
∴∠AOD=45°,
∵CD⊥AB,
∴AE=BE,△OAE为等腰直角三角形,
而CD=6cm,
∴OA=3cm,
∴AE=OA=cm,
∴AB=2AE=3(cm).
故答案为3.
13.解:连接AB,
∵BD⊥AO,
∴BE=ED=BD=4,
由勾股定理得,AB==2,
∵OF⊥BC,
∴CF=FB,又CO=OA,
∴OF=AB=(cm),
故答案为:.
14.解:连接OA,
∵OD⊥AB,
∴AD=AB=3m,
在Rt△AOD中,OA2=OD2+AD2,即OC2=(9﹣OC)2+32,
解得,OC=5m,
故答案为:5.
15.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0).
故答案为:(2,0)
16.解:∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠D=∠B=70°,
∴∠DAC=20°,
故答案为:20°.
17.解:连接OA、OP,连接OB交AP于H,
由圆周角定理得,∠AOB=2∠C=60°,
∵PB=AB,
∴∠POB=60°,OB⊥AP,
则AH=PH=OP×sin∠POH=,
∴AP=2AH=5,
故答案为:5.
18.解:过B作直径,连接AC交BO于点E,
∵点B为的中点,
∴BD⊥AC,
如图①,
∵点D恰在该圆直径的三等分点上,
∴BD=×2×3=2,
∴OD=OB﹣BD=1,
∵四边形ABCD是菱形,
∴DE=BD=1,
∴OE=2,
连接OC,
∵CE==,
∴边CD==;
如图②,BD=×2×3=4,
同理可得,OD=1,OE=1,DE=2,
连接OC,
∵CE===2,
∴边CD===2,
故答案为或2.
19.解:因为点A在圆O上,直线l过点A,
可得:m≤OA.
故答案为:m≤OA
20.解:过B作BD∥AC交x轴于D,
∵C是OB的中点,
∴OA=AD,
∴AC=BD,
∴当BD取最小值时,AC最小,
由图可知:当BD经过M时,线段BD的长最小,此时AC有最小值,
∵A(3,0),
∴D(6,0),
∵M(3,4),
∴DM==5,
∴BD=5﹣1=4,
∴AC=BD=2,即线段AC的最小值为2;
故答案为:2.
三.解答题
21.解:∵AB=CD,
∴=,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
22.解:(1)∵OD⊥AB,
∴=,
∴∠DOB=∠AOD=52°;
(2)设半径是r,
在直角△AOE中,OE2+AE2=OA2,
则(r﹣1)2+()2=r2,
解得r=4,
则CD=2r=8.
23.解:(1)如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=AB=6m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,
解得r=6.5.
(2)∵CD=4m,船舱顶部为长方形并高出水面3.4m,
∴CE=4﹣3.4=0.6(m),
∴OE=r﹣CE=6.5﹣0.6=5.9(m),
在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣5.92=7.44,
∴EN=(m).
∴MN=2EN=2×≈5.4m>5m.
∴此货船能顺利通过这座拱桥.
24.解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).
故答案为(2,0);
(3)圆的半径AM==2.
线段MD==<2,
所以点D在⊙M内.
25.解:过A作AC⊥BD于C,由题意得AB=400km,
∠DBA=45°,所以AC=BC.
在Rt△ABC中,设AC=BC=x.
由勾股定理,得AC2+BC2=AB2,所以x2+x2=4002,
所以AC=x=200≈282.8(km).
282.8km<300km.
所以A市将受到这次沙尘暴的影响.
26.证明:过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD
27.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴,即=,
∴AE=,
∴DE=.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
