数学必修二-2.1.3-2.1.4《空间直线与平面.平面与平面的位置关系》
文档属性
| 名称 | 数学必修二-2.1.3-2.1.4《空间直线与平面.平面与平面的位置关系》 |  | |
| 格式 | zip | ||
| 文件大小 | 332.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-20 09:26:55 | ||
图片预览




文档简介
(共17张PPT)
b
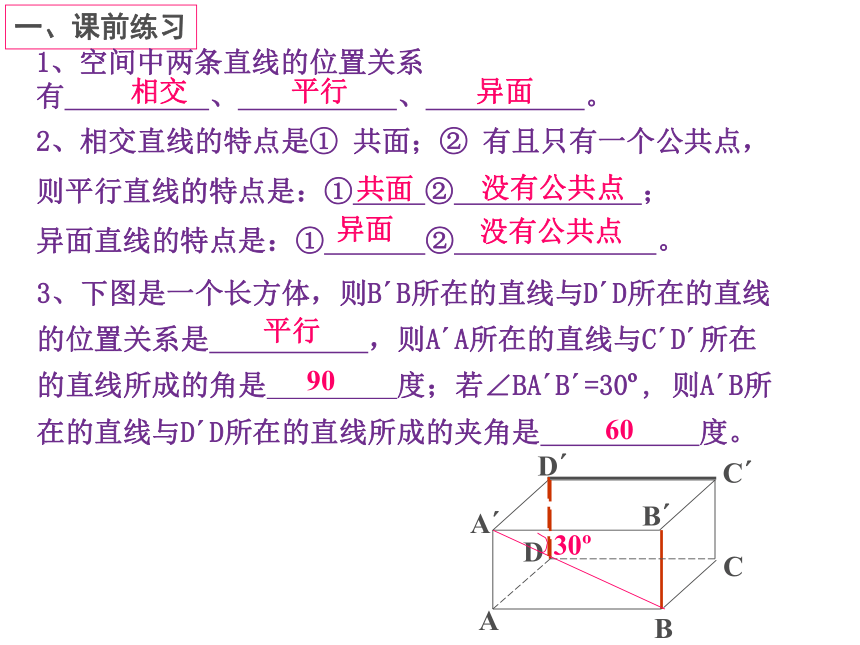
3、下图是一个长方体,则B B所在的直线与D D所在的直线的位置关系是 ,则A A所在的直线与C D 所在的直线所成的角是 度;若∠BA B =30 , 则A B所在的直线与D D所在的直线所成的夹角是 度。
一、课前练习
1、空间中两条直线的位置关系有 、 、 。
2、相交直线的特点是① 共面;② 有且只有一个公共点,则平行直线的特点是:① ② ;
异面直线的特点是:① ② 。
A
B
C
D
A
B
C
D
30
相交
平行
异面
共面
没有公共点
异面
没有公共点
平行
90
60
不同在 任何 一个平面内的两条直线叫做异面直线。
异面直线的定义:
相交直线
平行直线
异面直线
空间两直线的位置关系
上节回顾:
公理4:
在空间平行于同一条直线的两条直线互相平行.
异面直线的求法:
一作(找)二证三求
空间中,如果两个角的两边分别对应平行,
那么这两个角相等或互补.
等角定理:
异面直线的画法
用平面来衬托
异面直线所成的角
平移,转化为相交直线所成的角
A
B
G
F
H
E
D
C
上节回顾
如图,正方体ABCD-EFGH中,O为侧面ADHE的中心,求
(1)BE与CG所成的角?
(2)FO与BD所成的角?
解: (1)如图: ∵BF∥CG,∴∠EBF(或其补角)为异面直线 BE与CG所成的角,
又 BEF中∠EBF =45 , 所以BE与CG所成的角是45
o
o
O
连接HA、AF,
依题意知O为AH中点 , ∴∠HFO=30
o
(2)连接FH,
所以FO与BD所成的夹角是30
o
∴四边形BFHD为平行四边形,∴HF∥BD
∴∠HFO(或其补角)为异面直线 FO与BD所成的角
∵HD EA,EA FB ∴HD FB
∥
=
∥
=
∥
=
则AH=HF=FA
∴ △AFH为等边△
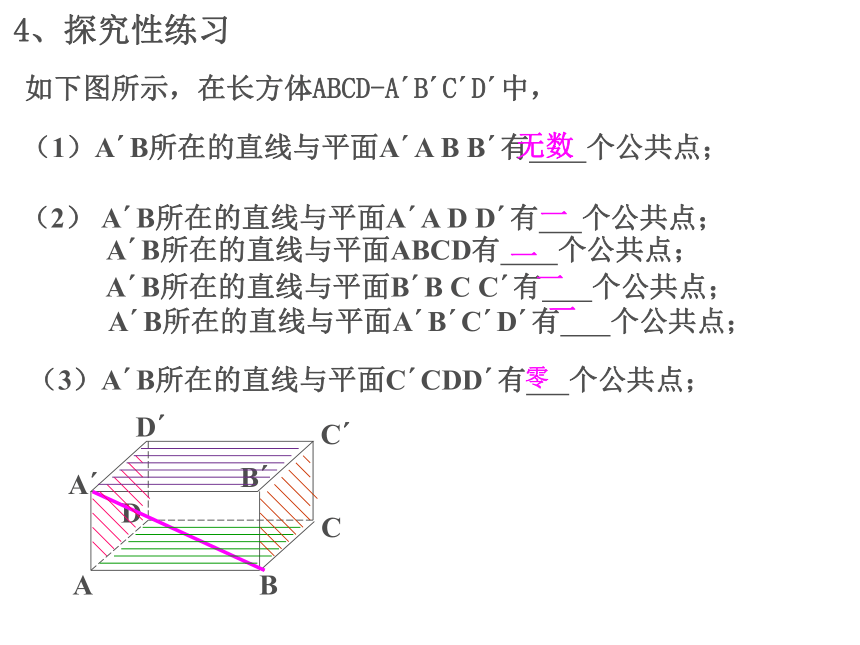
4、探究性练习
如下图所示,在长方体ABCD-A B C D 中,
(1)A B所在的直线与平面A A B B 有 个公共点;
(3)A B所在的直线与平面C CDD 有 个公共点;
C
D
A
B
C
D
A
B
(2) A B所在的直线与平面A A D D 有 个公共点;
A B所在的直线与平面B B C C 有 个公共点;
A B所在的直线与平面A B C D 有 个公共点;
A B所在的直线与平面ABCD有 个公共点;
无数
一
一
一
一
零
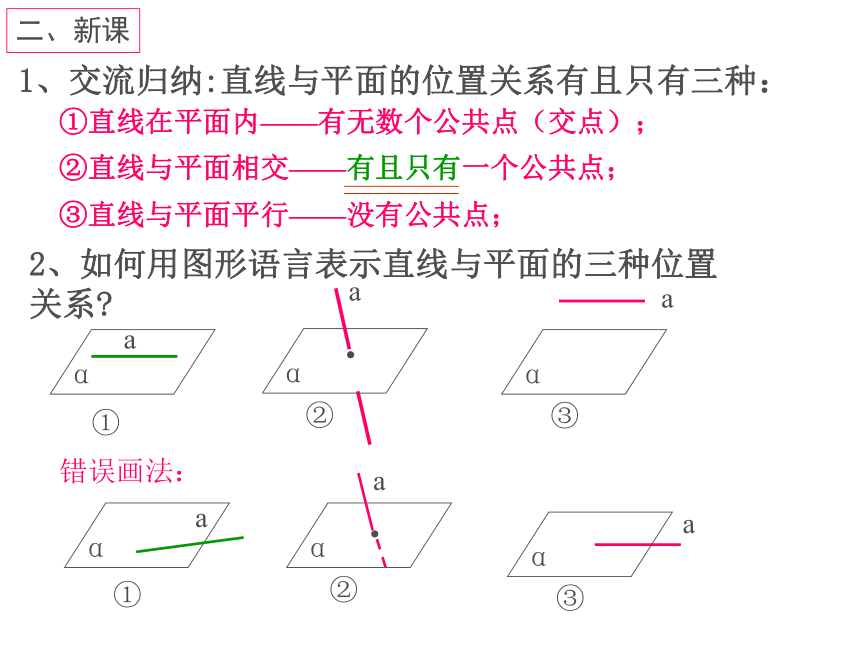
③直线与平面平行——没有公共点;
1、交流归纳:直线与平面的位置关系有且只有三种:
①直线在平面内——有无数个公共点(交点);
②直线与平面相交——有且只有一个公共点;
α
2、如何用图形语言表示直线与平面的三种位置关系
a
a
①
α
③
二、新课
a
α
②
错误画法:
α
a
α
②
①
a
a
α
③
3、如何用符号语言表示直线与平面的位置关系。
①直线a在平面α内,记作a α;
②直线a与平面α相交于A点,记作a∩α=A;
③直线a与平面α平行,记作a∥α;
④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点;( )
②若直线l与平面α平行,则l与平面α内的任意一条直线都平行;( )
4、判断正误
①若直线l上有无数个点不在平面α内,则l∥α; ( )
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;( )
l
α
α
l
b
c
α
l
b
⊙如果平面外的两条平行直线中的一条直线与平面平行,
那么另一条直线也与这个平面平行;( )
×
×
√
√
×
三、随堂练习
1、若直线a不平行于平面α ,且a α,
则下列结论成立的是( ):
(A)α内的所有直线与a异面 (B)α内不存在与a平行的直线;
(C)α内存在唯一的直线与a平行;(D)α内的直线与a都相交;
2、判断题:
(1)a∥α,b α,则a∥b;( )
(2)a α,则a∥α或a和α 相交;( )
(3)a∩α=A, a α; ( )
(4)若a α,b α,则a、b无公共点。 ( )
B
×
√
√
×
a
α
b
α
b
a
b
a
α
c
四、小结:
1、空间中直线与平面的三种位置关系:
直线在平面内——有无数个公共点(交点);
直线在平面外
相交——有且只有一个公共点;
平行——没有公共点;
2、用图形语言表示空间中直线与平面的三种位置关系:
3、用符号语言表示空间中直线与平面的三种关系:
① a α
② a∩α=A
③ a∥α
α
α
a
①
②
a
α
③
a
第一、二层的底面α和β无论怎样延伸都没有公共点;
前、后两面房顶γ和δ则有一条交线AB.
二层楼房示意图
探究平面与平面之间的位置关系
一、两个平面的位置关系
(1)两个平面平行
如果两个平面没有公共点,我们就说
这两个平面互相平行.
(2)两个平面相交
如果两个平面有公共点,它们就相交于一条过该公共点的直线,我们就说这两个平面相交 .
(3)两个平面的位置关系只有两种
①两个平面平行——没有公共点;记为
②两个平面相交——有一条公共直线,记为
两个平面的位置关系
两平面平行
没有公共点
有一条公共直线
两平面相交
α∥β
α∩β=a
位置关系
公共点
符号表示
图形表示
画两个互相平行的平面时,要注意使表示
平面的两个平行四边形的对应边平行,如图1,
而不应画成图2那样.
(4)两个平面平行的画法
图1
图2
五、小测:
(一)填空。
1、如果一条直线和一个平面 ,那么我们就说这条
直线和这个平面平行。
2、直线a在平面α外,是指直线a和平面α 或 。
3、直线与平面的位置关系按三种分为 或 或 。
按两种分为 或 。
(二)判断正误。
1、直线l平行于平面α内的无数条直线,则l∥α;( )
2、若直线a在平面α外,则a ∥α; ( )
3、若直线a ∥b,直线b α,则a ∥α; ( )
4、若直线a ∥b,b α,那么直线a就平行于平面α
内的无数条直线; ( )
(三)画出满足下列条件的图形。
a α,A∈α,A∈a,b∩α=A
没有公共点
相交
平行
相交
平行
直线在平面内
直线在平面内
直线在平面外
×
×
×
√
A
1.练习。P49-p50
b
3、下图是一个长方体,则B B所在的直线与D D所在的直线的位置关系是 ,则A A所在的直线与C D 所在的直线所成的角是 度;若∠BA B =30 , 则A B所在的直线与D D所在的直线所成的夹角是 度。
一、课前练习
1、空间中两条直线的位置关系有 、 、 。
2、相交直线的特点是① 共面;② 有且只有一个公共点,则平行直线的特点是:① ② ;
异面直线的特点是:① ② 。
A
B
C
D
A
B
C
D
30
相交
平行
异面
共面
没有公共点
异面
没有公共点
平行
90
60
不同在 任何 一个平面内的两条直线叫做异面直线。
异面直线的定义:
相交直线
平行直线
异面直线
空间两直线的位置关系
上节回顾:
公理4:
在空间平行于同一条直线的两条直线互相平行.
异面直线的求法:
一作(找)二证三求
空间中,如果两个角的两边分别对应平行,
那么这两个角相等或互补.
等角定理:
异面直线的画法
用平面来衬托
异面直线所成的角
平移,转化为相交直线所成的角
A
B
G
F
H
E
D
C
上节回顾
如图,正方体ABCD-EFGH中,O为侧面ADHE的中心,求
(1)BE与CG所成的角?
(2)FO与BD所成的角?
解: (1)如图: ∵BF∥CG,∴∠EBF(或其补角)为异面直线 BE与CG所成的角,
又 BEF中∠EBF =45 , 所以BE与CG所成的角是45
o
o
O
连接HA、AF,
依题意知O为AH中点 , ∴∠HFO=30
o
(2)连接FH,
所以FO与BD所成的夹角是30
o
∴四边形BFHD为平行四边形,∴HF∥BD
∴∠HFO(或其补角)为异面直线 FO与BD所成的角
∵HD EA,EA FB ∴HD FB
∥
=
∥
=
∥
=
则AH=HF=FA
∴ △AFH为等边△
4、探究性练习
如下图所示,在长方体ABCD-A B C D 中,
(1)A B所在的直线与平面A A B B 有 个公共点;
(3)A B所在的直线与平面C CDD 有 个公共点;
C
D
A
B
C
D
A
B
(2) A B所在的直线与平面A A D D 有 个公共点;
A B所在的直线与平面B B C C 有 个公共点;
A B所在的直线与平面A B C D 有 个公共点;
A B所在的直线与平面ABCD有 个公共点;
无数
一
一
一
一
零
③直线与平面平行——没有公共点;
1、交流归纳:直线与平面的位置关系有且只有三种:
①直线在平面内——有无数个公共点(交点);
②直线与平面相交——有且只有一个公共点;
α
2、如何用图形语言表示直线与平面的三种位置关系
a
a
①
α
③
二、新课
a
α
②
错误画法:
α
a
α
②
①
a
a
α
③
3、如何用符号语言表示直线与平面的位置关系。
①直线a在平面α内,记作a α;
②直线a与平面α相交于A点,记作a∩α=A;
③直线a与平面α平行,记作a∥α;
④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点;( )
②若直线l与平面α平行,则l与平面α内的任意一条直线都平行;( )
4、判断正误
①若直线l上有无数个点不在平面α内,则l∥α; ( )
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;( )
l
α
α
l
b
c
α
l
b
⊙如果平面外的两条平行直线中的一条直线与平面平行,
那么另一条直线也与这个平面平行;( )
×
×
√
√
×
三、随堂练习
1、若直线a不平行于平面α ,且a α,
则下列结论成立的是( ):
(A)α内的所有直线与a异面 (B)α内不存在与a平行的直线;
(C)α内存在唯一的直线与a平行;(D)α内的直线与a都相交;
2、判断题:
(1)a∥α,b α,则a∥b;( )
(2)a α,则a∥α或a和α 相交;( )
(3)a∩α=A, a α; ( )
(4)若a α,b α,则a、b无公共点。 ( )
B
×
√
√
×
a
α
b
α
b
a
b
a
α
c
四、小结:
1、空间中直线与平面的三种位置关系:
直线在平面内——有无数个公共点(交点);
直线在平面外
相交——有且只有一个公共点;
平行——没有公共点;
2、用图形语言表示空间中直线与平面的三种位置关系:
3、用符号语言表示空间中直线与平面的三种关系:
① a α
② a∩α=A
③ a∥α
α
α
a
①
②
a
α
③
a
第一、二层的底面α和β无论怎样延伸都没有公共点;
前、后两面房顶γ和δ则有一条交线AB.
二层楼房示意图
探究平面与平面之间的位置关系
一、两个平面的位置关系
(1)两个平面平行
如果两个平面没有公共点,我们就说
这两个平面互相平行.
(2)两个平面相交
如果两个平面有公共点,它们就相交于一条过该公共点的直线,我们就说这两个平面相交 .
(3)两个平面的位置关系只有两种
①两个平面平行——没有公共点;记为
②两个平面相交——有一条公共直线,记为
两个平面的位置关系
两平面平行
没有公共点
有一条公共直线
两平面相交
α∥β
α∩β=a
位置关系
公共点
符号表示
图形表示
画两个互相平行的平面时,要注意使表示
平面的两个平行四边形的对应边平行,如图1,
而不应画成图2那样.
(4)两个平面平行的画法
图1
图2
五、小测:
(一)填空。
1、如果一条直线和一个平面 ,那么我们就说这条
直线和这个平面平行。
2、直线a在平面α外,是指直线a和平面α 或 。
3、直线与平面的位置关系按三种分为 或 或 。
按两种分为 或 。
(二)判断正误。
1、直线l平行于平面α内的无数条直线,则l∥α;( )
2、若直线a在平面α外,则a ∥α; ( )
3、若直线a ∥b,直线b α,则a ∥α; ( )
4、若直线a ∥b,b α,那么直线a就平行于平面α
内的无数条直线; ( )
(三)画出满足下列条件的图形。
a α,A∈α,A∈a,b∩α=A
没有公共点
相交
平行
相交
平行
直线在平面内
直线在平面内
直线在平面外
×
×
×
√
A
1.练习。P49-p50
