1.3.1单调性与最大(小)值
图片预览



文档简介
(共29张PPT)
1.1 集合
1.1.1 集合的含义与表示(1课时)
1.1.2 集合间的基本关系(1课时)
1.1.3 集合的基本运算(1课时)
1.2 函数及其表示
1.2.1 函数的概念(1课时)
1.2.2 函数的表示方法(2课时)
1.3 函数的基本性质
1.3.1 函数的单调性与最大(小)值(2课时)
1.3.2 奇偶性(1课时)
第一章复习与测试
(1)课本从大家熟悉的集合出发,给出元素、集合的含义及表示方法;通过类比实数间的大小关系、运算引入集合间的关系、运算,同时介绍子集和全集等概念.
(2)函数是中学数学最重要的基本概念之一.函数分两阶段学习:(初中)函数概念、正(反)比例函数、一次函数、二次函数及其图像和性质.(高一必修)函数概念、基本性质、基本初等函数(I、II).(高二选修)导数及其应用.
(3)实习作业:收集17世纪前后对数学发展起重大作用的历史事件和人物(开普勒、伽利略、笛卡尔、牛顿、莱布尼兹、欧拉等)的有关资料.
本章内容简介
学习目标
1.通过对已学函数图象的观察,理解函数的单调性及其几何意义.能根据图象的升降特征,划分函数的单调区间.理解增(减)函数的定义,会证明函数在指定区间上的单调性.
2.通过对一些熟悉函数的观察,理解函数最大(小)值的定义,并会利用单调性求其最值.
3.理解函数奇偶性的含义,体会此时函数图像的特征.会用奇偶性的定义判断函数的奇偶性.
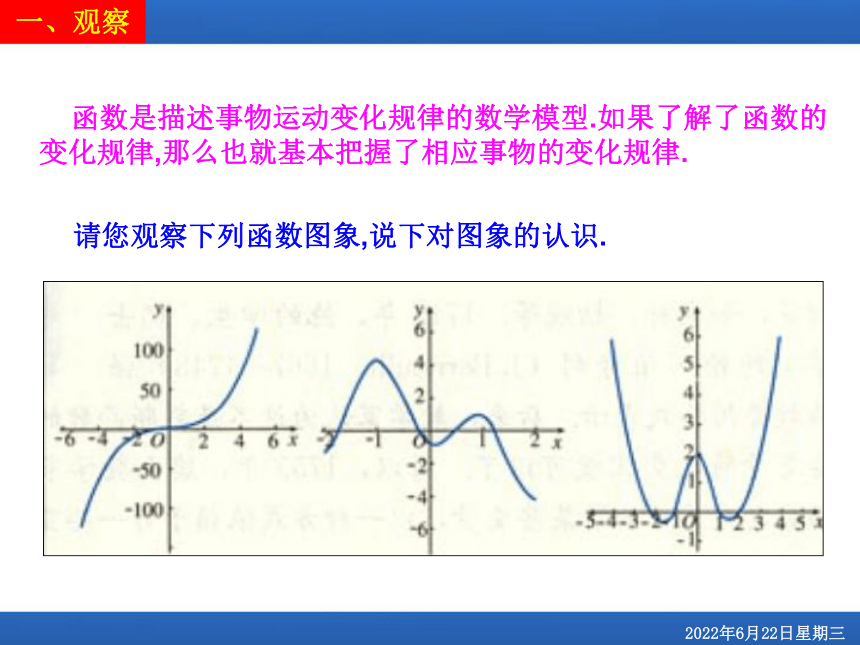
函数是描述事物运动变化规律的数学模型.如果了解了函数的变化规律,那么也就基本把握了相应事物的变化规律.
请您观察下列函数图象,说下对图象的认识.
一、观察
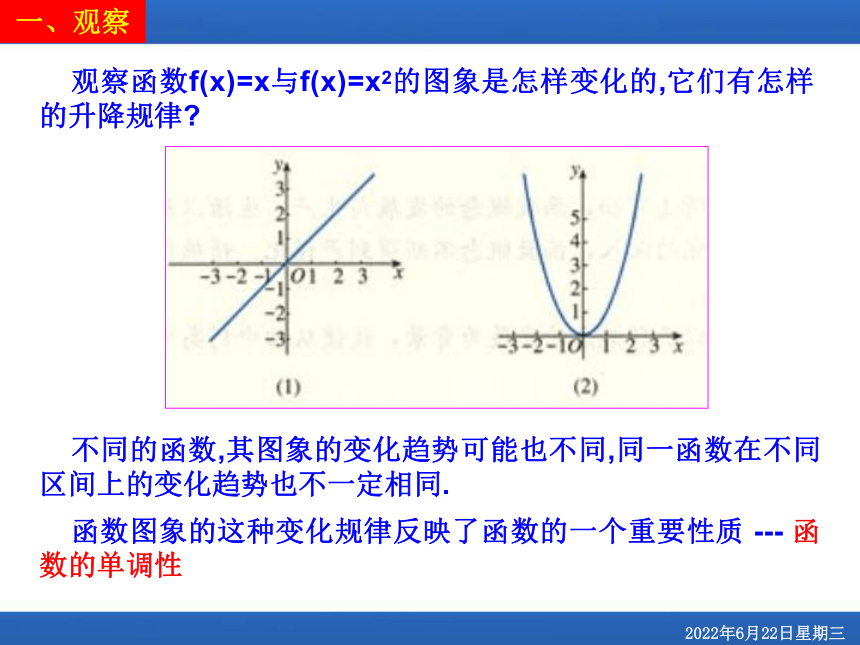
观察函数f(x)=x与f(x)=x2的图象是怎样变化的,它们有怎样的升降规律
不同的函数,其图象的变化趋势可能也不同,同一函数在不同区间上的变化趋势也不一定相同.
函数图象的这种变化规律反映了函数的一个重要性质 --- 函数的单调性
一、观察
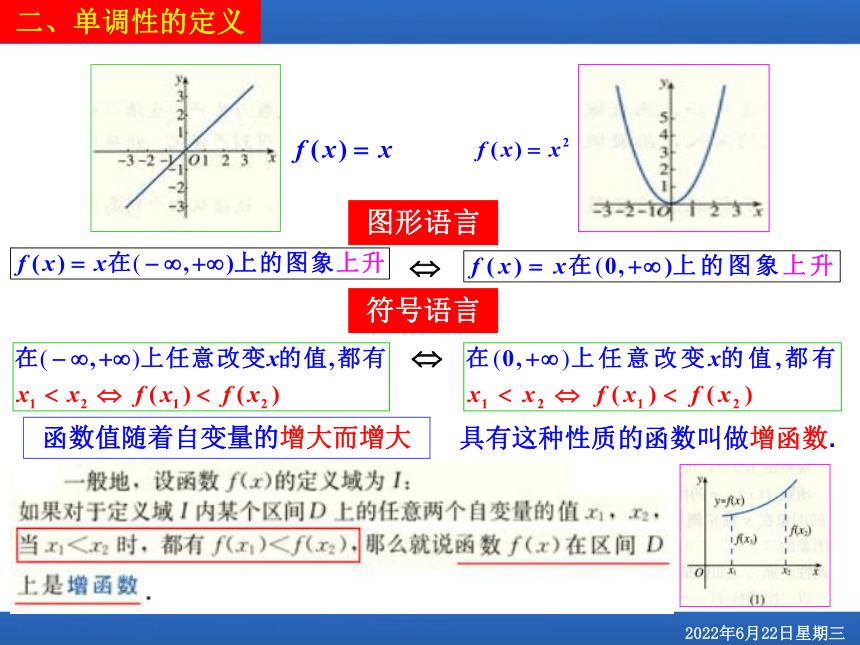
函数值随着自变量的增大而增大
具有这种性质的函数叫做增函数.
二、单调性的定义
图形语言
符号语言
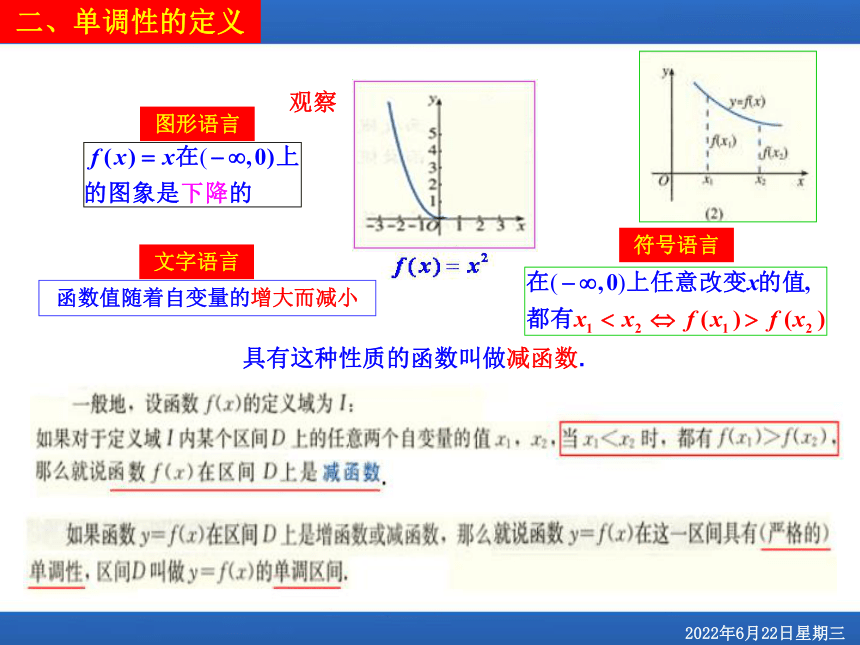
二、单调性的定义
具有这种性质的函数叫做减函数.
图形语言
符号语言
函数值随着自变量的增大而减小
文字语言
三、例题
三、例题
三、例题
请您观察下列图象,比较两个函数图象及其值域,您能发现什么
四、最大(小)值
请您观察函数图象,说明最大值的含义
四、最大(小)值
四、最大(小)值
对于不熟悉的函数,可以先画出图象,观察其单调性,再用定义证明,然后利用单调性求出函数的最值.
四、最大(小)值
四、最大(小)值
1、函数单调性的定义
五、小结
3、求函数最值的一般方法
(1) 对于熟悉的正比例函数、反比例函数、一次函数和二次函数等,可以先画出在其定义域的图象求其最值.
(2) 对于不熟悉的函数可以先画出其图象,观察其单调性,再用定义证明,然后利用单调性求其最值.
2、用定义证明函数的单调性
五、小结
P39)A1、A2 、A5、B2
课堂作业
1.1 集合
1.1.1 集合的含义与表示(1课时)
1.1.2 集合间的基本关系(1课时)
1.1.3 集合的基本运算(1课时)
1.2 函数及其表示
1.2.1 函数的概念(1课时)
1.2.2 函数的表示方法(2课时)
1.3 函数的基本性质
1.3.1 函数的单调性与最大(小)值(2课时)
1.3.2 奇偶性(1课时)
第一章复习与测试
(1)课本从大家熟悉的集合出发,给出元素、集合的含义及表示方法;通过类比实数间的大小关系、运算引入集合间的关系、运算,同时介绍子集和全集等概念.
(2)函数是中学数学最重要的基本概念之一.函数分两阶段学习:(初中)函数概念、正(反)比例函数、一次函数、二次函数及其图像和性质.(高一必修)函数概念、基本性质、基本初等函数(I、II).(高二选修)导数及其应用.
(3)实习作业:收集17世纪前后对数学发展起重大作用的历史事件和人物(开普勒、伽利略、笛卡尔、牛顿、莱布尼兹、欧拉等)的有关资料.
本章内容简介
学习目标
1.通过对已学函数图象的观察,理解函数的单调性及其几何意义.能根据图象的升降特征,划分函数的单调区间.理解增(减)函数的定义,会证明函数在指定区间上的单调性.
2.通过对一些熟悉函数的观察,理解函数最大(小)值的定义,并会利用单调性求其最值.
3.理解函数奇偶性的含义,体会此时函数图像的特征.会用奇偶性的定义判断函数的奇偶性.
函数是描述事物运动变化规律的数学模型.如果了解了函数的变化规律,那么也就基本把握了相应事物的变化规律.
请您观察下列函数图象,说下对图象的认识.
一、观察
观察函数f(x)=x与f(x)=x2的图象是怎样变化的,它们有怎样的升降规律
不同的函数,其图象的变化趋势可能也不同,同一函数在不同区间上的变化趋势也不一定相同.
函数图象的这种变化规律反映了函数的一个重要性质 --- 函数的单调性
一、观察
函数值随着自变量的增大而增大
具有这种性质的函数叫做增函数.
二、单调性的定义
图形语言
符号语言
二、单调性的定义
具有这种性质的函数叫做减函数.
图形语言
符号语言
函数值随着自变量的增大而减小
文字语言
三、例题
三、例题
三、例题
请您观察下列图象,比较两个函数图象及其值域,您能发现什么
四、最大(小)值
请您观察函数图象,说明最大值的含义
四、最大(小)值
四、最大(小)值
对于不熟悉的函数,可以先画出图象,观察其单调性,再用定义证明,然后利用单调性求出函数的最值.
四、最大(小)值
四、最大(小)值
1、函数单调性的定义
五、小结
3、求函数最值的一般方法
(1) 对于熟悉的正比例函数、反比例函数、一次函数和二次函数等,可以先画出在其定义域的图象求其最值.
(2) 对于不熟悉的函数可以先画出其图象,观察其单调性,再用定义证明,然后利用单调性求其最值.
2、用定义证明函数的单调性
五、小结
P39)A1、A2 、A5、B2
课堂作业
