八年级数学第十八章勾股定理
图片预览





文档简介
(共64张PPT)
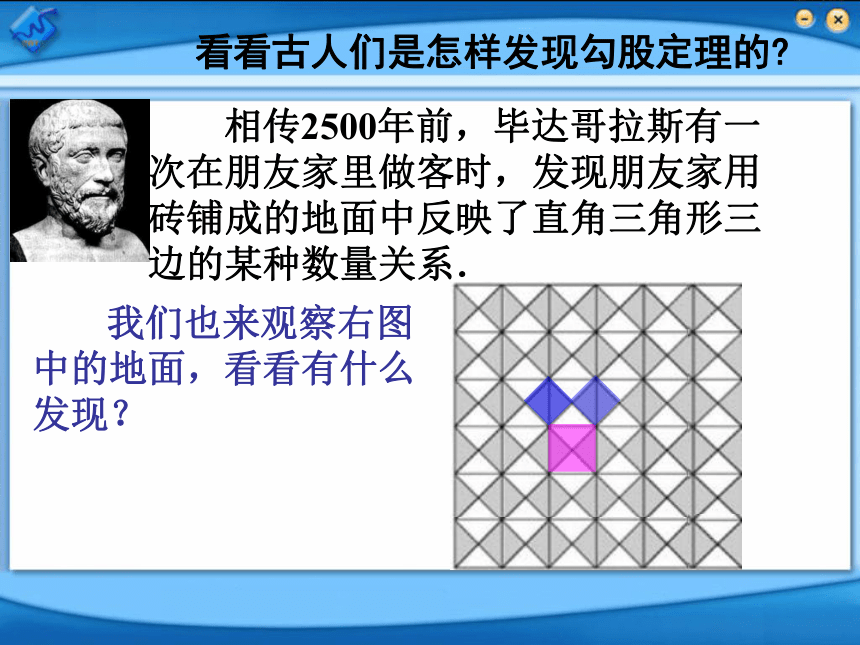
看看古人们是怎样发现勾股定理的
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
(图中每一格代表一平方厘米)
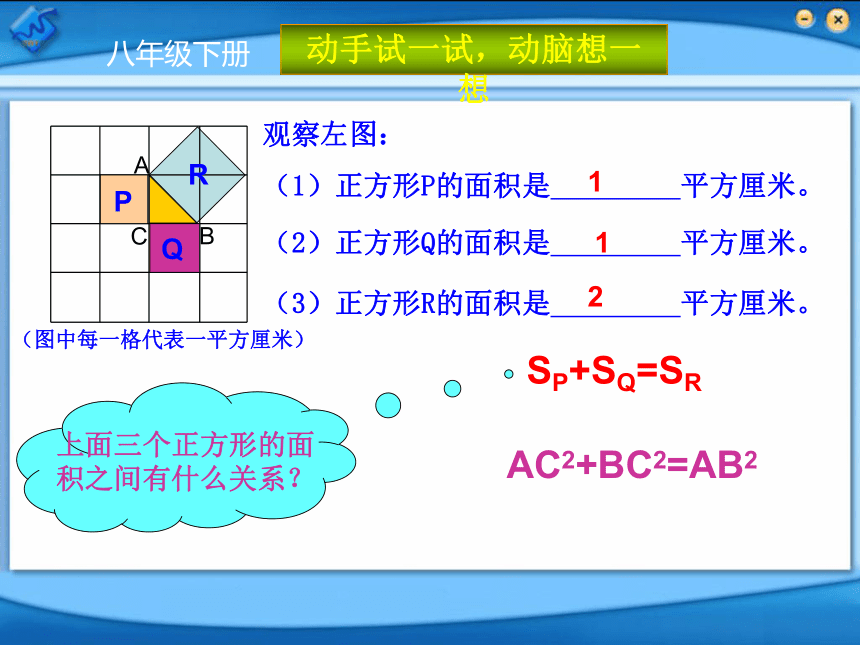
观察左图:
(1)正方形P的面积是 平方厘米。
(2)正方形Q的面积是 平方厘米。
(3)正方形R的面积是 平方厘米。
1
2
1
上面三个正方形的面积之间有什么关系?
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
八年级下册
动手试一试,动脑想一想
A
B
C
R
Q
P
(图中每一格代表一平方厘米)
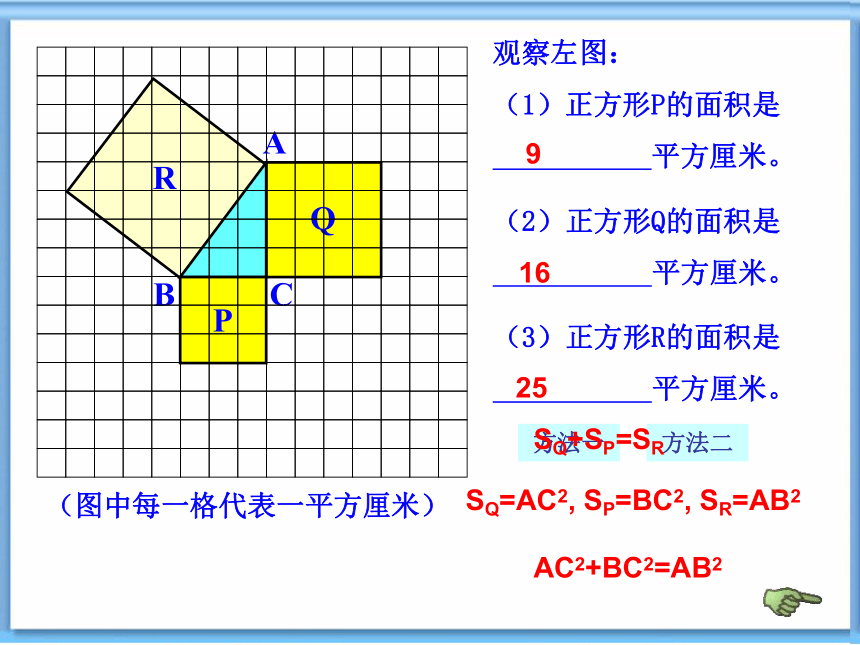
观察左图:
(1)正方形P的面积是
平方厘米。
(2)正方形Q的面积是
平方厘米。
(3)正方形R的面积是
平方厘米。
9
方法二
16
25
SQ=AC2, SP=BC2, SR=AB2
方法一
AC2+BC2=AB2
SQ+SP=SR
A
B
C
R
Q
P
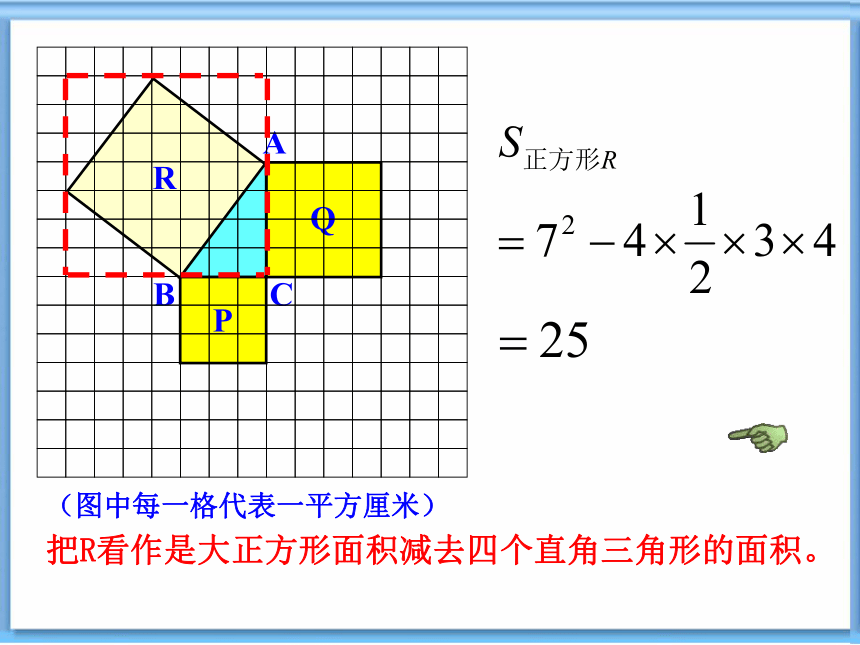
把R看作是大正方形面积减去四个直角三角形的面积。
(图中每一格代表一平方厘米)
A
B
C
R
Q
P
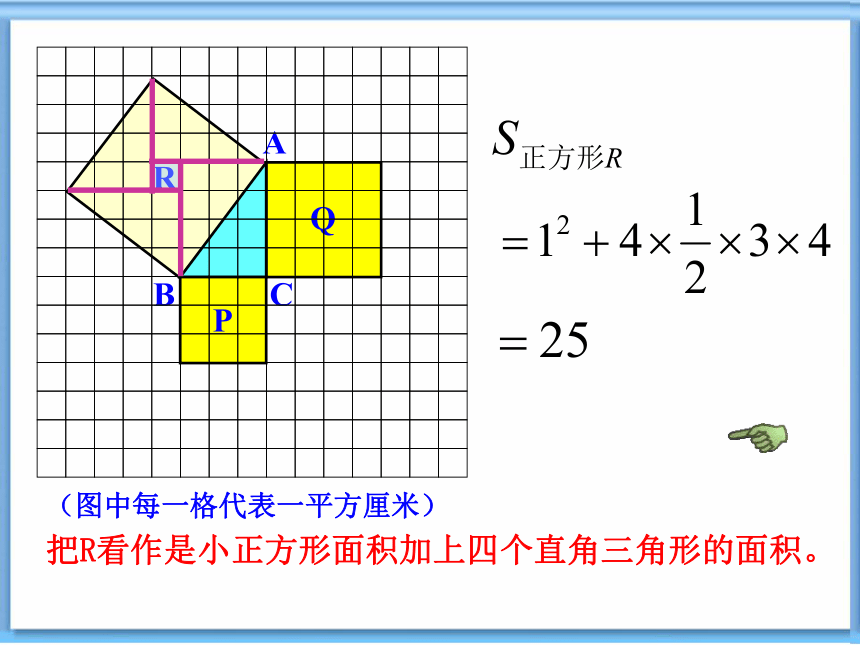
把R看作是小正方形面积加上四个直角三角形的面积。
(图中每一格代表一平方厘米)
勾股定理(在西方又称为毕达哥拉斯定理)
直角三角形的两直角边的平方和等于斜边的平方。
A
B
C
在 ABC中, C=90
即AC2+BC2=AB2
a
b
c
(a2+b2=c2)
勾
股
弦
八年级下册
勾股定理
A
B
C
a
b
c
直角边2+直角边2=斜边2
a
a
a
b
b
b
c
c
c
大正方形的面积可以表示为:
你能通过下图证明勾股定理吗?
a
b
c
所以:
化简得:
八年级下册
勾股定理-----证明
a
b
c
你能通过下图证明勾股定理吗?
大正方形的面积可以表示为:
所以:
化简得:
八年级下册
勾股定理
勾股定理-----证明
结论:在直角三角形中,已知两边可以求第三边.
例1 如图,在Rt△ABC中,BC=24,AC=7,求AB的长.
B
24
A
C
7
如果将题目变为:
在Rt△ABC中,AB=41, BC=40,求AC的长呢?
八年级下册
勾股定理----理解
1.在Rt△ABC中,AB=c,BC=a,AC=b, ∠C=90°,
(1)已知a=3,b=4,则c=______;(2)已知a=6,c=10,则b=_____;
(3)已知a=2,b=4,则c=______.
2.已知Rt△ABC中,∠B= 90°,AC= ,BC=
则AB=_______, ∠A=________;
3.在平面直角坐标系中,点(-3,-4)与原点之间的
距离是_______,点(3,- 4)与点(2,1)之间的距离是_______.
动脑想一想,看谁反应快!!
5
8
450
5
5. 若正方形的面积为3cm2,则它的对角线长是 .
6. 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .
4.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=8,b=15,则c=______.
6
8
17
新知理解----试一试
6,8,10
八年级下册
7、如图,在△ABC中,∠ACB = 90。,CD是高,若AB=13cm,AC = 5cm,求CD的长;
A
B
C
D
八年级下册
勾股定理---运用
8.△ABC中,周长是24,∠C=90°,且 b=6,则三角形的面积是多少
A
B
C
a
b
c
八年级下册
勾股定理
勾股定理---运用
作业:
(1)课本P69第1、2、3题
(2)《全效学习》P48-50
例2、已知三角形ABC中,AB=10,BC=21,AC=17,求BC边上的高线AD。
A
B
C
D
1.△ABC中,周长是 , ∠C=90°,且 c=2,则三角形的面积是多少
A
B
C
a
b
c
八年级下册
勾股定理
勾股定理---运用
2.直角三角形中,斜边长是 , 面积为2,则三角形的周长是多少
3、如图,在Rt△ABC中 C=90 ,AC=BC,且BC=5, 求三角形ABC的面积和底边上的高
A
B
C
4、如图,在Rt△ABC中 C=90 , A=30 ,,且AC=3, 求BC的长和三角形ABC的面积
A
B
C
5.如图,△ABC中,∠A=45°, ∠B=30°,BC=8. 求AC的长.
A
B
C
D
8
4
4
八年级下册
勾股定理---运用
6.如图,四边形ABCD中,∠B=∠D=90°,
∠C=45°,AD=1,BC=2,求CD的长.
A
B
C
D
E
1
2
450
450
1
2
八年级下册
勾股定理
勾股定理---运用
7.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 ,AD = 3,AB = 4,BC = 12,求CD和四边形ABCD的面积;
D
A
B
C
八年级下册
勾股定理
勾股定理---运用
8.在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积。
A
B
C
D
13
13
10
八年级下册
勾股定理
勾股定理---运用
9、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
11.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求(1)BD (2)CD (3)BC
∟
D
∟
D
A
B
C
10.已知:直角三角形的三边长分别是3,4,X,则X=
A
B
C
12.如图,在△ABC中,AB=AC=5,P为BC边上任意一点.求证:AP2+PB·PC=25.
A
B
C
P
D
八年级下册
勾股定理---运用
13.在长和宽分别是40cm,30cm的文具盒中,能放进一支长为48cm的铅笔吗?
40cm
30cm
x
八年级下册
勾股定理
勾股定理---运用
14、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离。
A
B
C
40
90
160
40
八年级下册
勾股定理
勾股定理---运用
15.飞机在天空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,飞机每时飞行多少千米
20秒
4000米
5000米
A
B
C
16.如图,在水塔O的东北方向处有一抽水站A距O点8千米,在水塔的东南向处有一建筑工地B距O点6千米,在AB间建一条直水管,则水管的长为多少
o
八年级下册
勾股定理
勾股定理---运用
17、甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6千米/小时的速度向东行走,1时后乙出发,他以5千米/小时的速度向北行进,上午10:00,甲、乙二人相距多远
东
北
甲
乙
八年级下册
勾股定理
勾股定理---运用
18、某市要建造一图书馆,位置在如图所示的直线AB上选取,该市有两所学校在点C和点D的位置,CA⊥AB于A,DB⊥AB于B,已知AB=25千米,CA=15千米,DB=10千米,试问:图书馆E应该建在距点A多少千米处,才能使它到两所学校的距离相等?
A
C
E
B
D
x
19.有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
水池
八年级下册
勾股定理
勾股定理---运用
作业:
(1)课本P70第4、5、6题
(2)《全效学习》P51-53
20、如图,在直角三角形ABC中,∠C=90°,BC=3cm,AC=4cm,折叠∠CBA,使BC边的点落在AB边上,其中点C落在点E处,求CD的长。
B
C
A
D
E
八年级下册
勾股定理
勾股定理---运用
21、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求(1)CF (2)EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
A
B
我怎么走
会最近呢
22.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
26.如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少?
B
C
A
B1
C1
D1
A1
D
B
A
B1
D1
A1
D
C1
C
23、如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
E
F
D
23、如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
B
5
10
20
A
C
E
10
20
A
C
F
A
E
C
B
20
15
10
E
F
D
24. 一天,小明买了一张底面是边长为260cm正方形,厚30cm的床垫回家。到了家门口,才发现门口只有242cm高,宽100cm。你认为小明能拿进屋吗,为什么?
242
100
八年级下册
勾股定理
勾股定理---运用
25、小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的34英寸或86厘米的电视机,是指其荧屏对角线的长度
∴售货员没搞错
荧屏对角线大约为86厘米
∵702+502=7400
862=7396
八年级下册
勾股定理
勾股定理---运用
27、在下图中,BC长为3厘米,AB长为4厘米,AF长为12厘米,求正方形CDEF的面积。
A
B
C
D
E
F
AC2=32+42=52
SCDEF=FC2=AF2+AC2=122+52
=132=169厘米2
28、如图,直角三角形三边上的半圆面积之间有什么关系?
S1
S2
S3
S1+S2=S3
即:两直角边上的半圆面积之和等于斜边上半圆的面积。
29、一架云梯长25米,斜靠在一面墙上,梯子底端离墙7米。
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向也滑动了4米吗?
30、郑凯想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出旗杆的高吗?
A
B
C
5米
(X+1)米
x米
31、如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
32、已知:在Rt△ABC中,∠C=900, ∠A,∠B,∠C的对边分别为a,b,c,设△ABC的面积为S,周长为P
(1)填表:
三边a b c a+b-c
3、4、5 2
5、12、13 4
8、15、17 6
(2)如果a+b-c=m,
观察上表猜想
=_______
(用含有m的代数式表示)。
(3)证明(2)中的结论。
作业:
(1)课本P70第7、8、9题
(2)《全效学习》P53-55
八年级下册
勾股定理
X
∵边长取正值
a
b
B'
C'
A'
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2
求证:△ABC是直角三角形
∴ △ ABC是直角三角形
证明:
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。且边C所对的角为直角。
a2 + b2 = c2
互逆命题
逆定理
定理
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17
例题解析
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
13
A
B
C
D
A
B
C
D
3
4
5
12
例2 一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸如右图所示,这个 零件符合要求吗?
例题解析
B
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
1.
练一练
2、已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
S四边形ABCD=36
中考链接
作业: 1、P76页,第1、4、6题 2《全》P58-59
练一练
3、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
思维训练
1、一个零件的形状如下图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗 四边形ABCD的面积是多少
2、 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.
思维训练
驶向胜利的彼岸
定理与逆定理
开启 智慧
我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.
想一想:
互逆命题与互逆定理有何关系
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.
说出下列命题的逆命题.这些命题的逆命题成立吗
逆命题: 内错角相等,两条直线平行. 成立
逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立
逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立
逆命题:对应角相等的两个三角形是全等三角形. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
试一试
一个命题是真命题,它逆命题却不一定是真命题.
作业: 1、《全》P60
看看古人们是怎样发现勾股定理的
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
(图中每一格代表一平方厘米)
观察左图:
(1)正方形P的面积是 平方厘米。
(2)正方形Q的面积是 平方厘米。
(3)正方形R的面积是 平方厘米。
1
2
1
上面三个正方形的面积之间有什么关系?
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
八年级下册
动手试一试,动脑想一想
A
B
C
R
Q
P
(图中每一格代表一平方厘米)
观察左图:
(1)正方形P的面积是
平方厘米。
(2)正方形Q的面积是
平方厘米。
(3)正方形R的面积是
平方厘米。
9
方法二
16
25
SQ=AC2, SP=BC2, SR=AB2
方法一
AC2+BC2=AB2
SQ+SP=SR
A
B
C
R
Q
P
把R看作是大正方形面积减去四个直角三角形的面积。
(图中每一格代表一平方厘米)
A
B
C
R
Q
P
把R看作是小正方形面积加上四个直角三角形的面积。
(图中每一格代表一平方厘米)
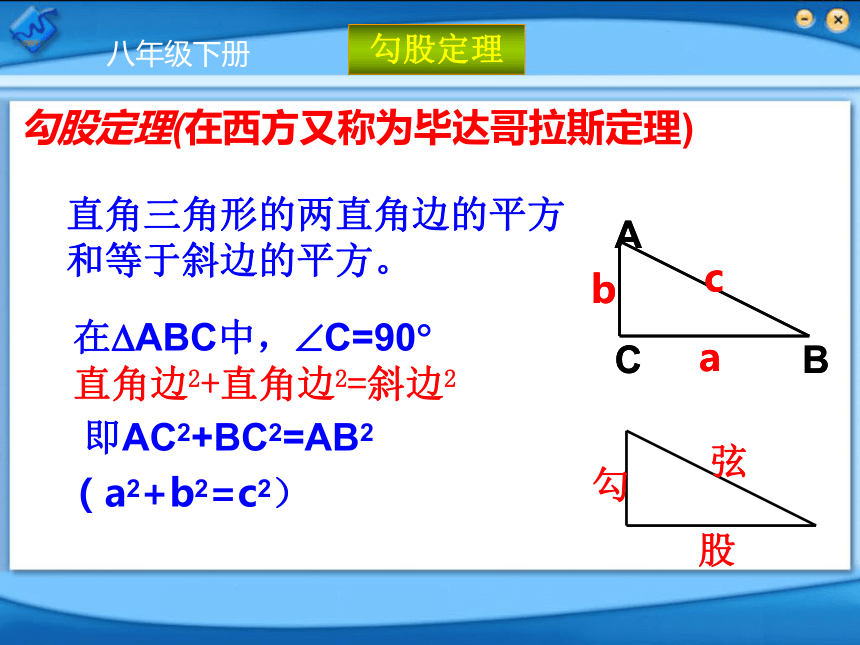
勾股定理(在西方又称为毕达哥拉斯定理)
直角三角形的两直角边的平方和等于斜边的平方。
A
B
C
在 ABC中, C=90
即AC2+BC2=AB2
a
b
c
(a2+b2=c2)
勾
股
弦
八年级下册
勾股定理
A
B
C
a
b
c
直角边2+直角边2=斜边2
a
a
a
b
b
b
c
c
c
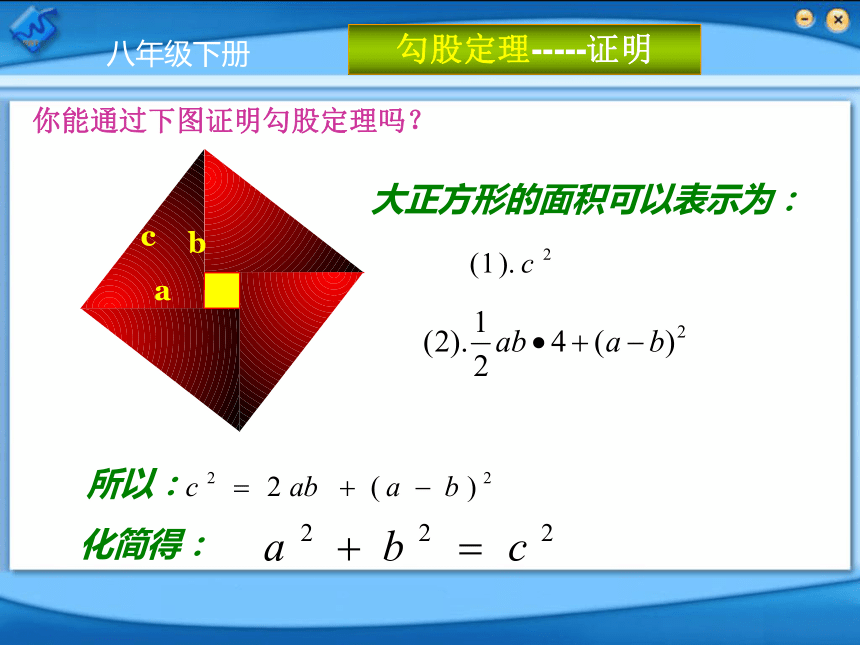
大正方形的面积可以表示为:
你能通过下图证明勾股定理吗?
a
b
c
所以:
化简得:
八年级下册
勾股定理-----证明
a
b
c
你能通过下图证明勾股定理吗?
大正方形的面积可以表示为:
所以:
化简得:
八年级下册
勾股定理
勾股定理-----证明
结论:在直角三角形中,已知两边可以求第三边.
例1 如图,在Rt△ABC中,BC=24,AC=7,求AB的长.
B
24
A
C
7
如果将题目变为:
在Rt△ABC中,AB=41, BC=40,求AC的长呢?
八年级下册
勾股定理----理解
1.在Rt△ABC中,AB=c,BC=a,AC=b, ∠C=90°,
(1)已知a=3,b=4,则c=______;(2)已知a=6,c=10,则b=_____;
(3)已知a=2,b=4,则c=______.
2.已知Rt△ABC中,∠B= 90°,AC= ,BC=
则AB=_______, ∠A=________;
3.在平面直角坐标系中,点(-3,-4)与原点之间的
距离是_______,点(3,- 4)与点(2,1)之间的距离是_______.
动脑想一想,看谁反应快!!
5
8
450
5
5. 若正方形的面积为3cm2,则它的对角线长是 .
6. 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .
4.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=8,b=15,则c=______.
6
8
17
新知理解----试一试
6,8,10
八年级下册
7、如图,在△ABC中,∠ACB = 90。,CD是高,若AB=13cm,AC = 5cm,求CD的长;
A
B
C
D
八年级下册
勾股定理---运用
8.△ABC中,周长是24,∠C=90°,且 b=6,则三角形的面积是多少
A
B
C
a
b
c
八年级下册
勾股定理
勾股定理---运用
作业:
(1)课本P69第1、2、3题
(2)《全效学习》P48-50
例2、已知三角形ABC中,AB=10,BC=21,AC=17,求BC边上的高线AD。
A
B
C
D
1.△ABC中,周长是 , ∠C=90°,且 c=2,则三角形的面积是多少
A
B
C
a
b
c
八年级下册
勾股定理
勾股定理---运用
2.直角三角形中,斜边长是 , 面积为2,则三角形的周长是多少
3、如图,在Rt△ABC中 C=90 ,AC=BC,且BC=5, 求三角形ABC的面积和底边上的高
A
B
C
4、如图,在Rt△ABC中 C=90 , A=30 ,,且AC=3, 求BC的长和三角形ABC的面积
A
B
C
5.如图,△ABC中,∠A=45°, ∠B=30°,BC=8. 求AC的长.
A
B
C
D
8
4
4
八年级下册
勾股定理---运用
6.如图,四边形ABCD中,∠B=∠D=90°,
∠C=45°,AD=1,BC=2,求CD的长.
A
B
C
D
E
1
2
450
450
1
2
八年级下册
勾股定理
勾股定理---运用
7.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 ,AD = 3,AB = 4,BC = 12,求CD和四边形ABCD的面积;
D
A
B
C
八年级下册
勾股定理
勾股定理---运用
8.在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积。
A
B
C
D
13
13
10
八年级下册
勾股定理
勾股定理---运用
9、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
11.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求(1)BD (2)CD (3)BC
∟
D
∟
D
A
B
C
10.已知:直角三角形的三边长分别是3,4,X,则X=
A
B
C
12.如图,在△ABC中,AB=AC=5,P为BC边上任意一点.求证:AP2+PB·PC=25.
A
B
C
P
D
八年级下册
勾股定理---运用
13.在长和宽分别是40cm,30cm的文具盒中,能放进一支长为48cm的铅笔吗?
40cm
30cm
x
八年级下册
勾股定理
勾股定理---运用
14、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离。
A
B
C
40
90
160
40
八年级下册
勾股定理
勾股定理---运用
15.飞机在天空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,飞机每时飞行多少千米
20秒
4000米
5000米
A
B
C
16.如图,在水塔O的东北方向处有一抽水站A距O点8千米,在水塔的东南向处有一建筑工地B距O点6千米,在AB间建一条直水管,则水管的长为多少
o
八年级下册
勾股定理
勾股定理---运用
17、甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6千米/小时的速度向东行走,1时后乙出发,他以5千米/小时的速度向北行进,上午10:00,甲、乙二人相距多远
东
北
甲
乙
八年级下册
勾股定理
勾股定理---运用
18、某市要建造一图书馆,位置在如图所示的直线AB上选取,该市有两所学校在点C和点D的位置,CA⊥AB于A,DB⊥AB于B,已知AB=25千米,CA=15千米,DB=10千米,试问:图书馆E应该建在距点A多少千米处,才能使它到两所学校的距离相等?
A
C
E
B
D
x
19.有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
水池
八年级下册
勾股定理
勾股定理---运用
作业:
(1)课本P70第4、5、6题
(2)《全效学习》P51-53
20、如图,在直角三角形ABC中,∠C=90°,BC=3cm,AC=4cm,折叠∠CBA,使BC边的点落在AB边上,其中点C落在点E处,求CD的长。
B
C
A
D
E
八年级下册
勾股定理
勾股定理---运用
21、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求(1)CF (2)EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
A
B
我怎么走
会最近呢
22.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
26.如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少?
B
C
A
B1
C1
D1
A1
D
B
A
B1
D1
A1
D
C1
C
23、如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
E
F
D
23、如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
B
5
10
20
A
C
E
10
20
A
C
F
A
E
C
B
20
15
10
E
F
D
24. 一天,小明买了一张底面是边长为260cm正方形,厚30cm的床垫回家。到了家门口,才发现门口只有242cm高,宽100cm。你认为小明能拿进屋吗,为什么?
242
100
八年级下册
勾股定理
勾股定理---运用
25、小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的34英寸或86厘米的电视机,是指其荧屏对角线的长度
∴售货员没搞错
荧屏对角线大约为86厘米
∵702+502=7400
862=7396
八年级下册
勾股定理
勾股定理---运用
27、在下图中,BC长为3厘米,AB长为4厘米,AF长为12厘米,求正方形CDEF的面积。
A
B
C
D
E
F
AC2=32+42=52
SCDEF=FC2=AF2+AC2=122+52
=132=169厘米2
28、如图,直角三角形三边上的半圆面积之间有什么关系?
S1
S2
S3
S1+S2=S3
即:两直角边上的半圆面积之和等于斜边上半圆的面积。
29、一架云梯长25米,斜靠在一面墙上,梯子底端离墙7米。
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向也滑动了4米吗?
30、郑凯想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出旗杆的高吗?
A
B
C
5米
(X+1)米
x米
31、如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
32、已知:在Rt△ABC中,∠C=900, ∠A,∠B,∠C的对边分别为a,b,c,设△ABC的面积为S,周长为P
(1)填表:
三边a b c a+b-c
3、4、5 2
5、12、13 4
8、15、17 6
(2)如果a+b-c=m,
观察上表猜想
=_______
(用含有m的代数式表示)。
(3)证明(2)中的结论。
作业:
(1)课本P70第7、8、9题
(2)《全效学习》P53-55
八年级下册
勾股定理
X
∵边长取正值
a
b
B'
C'
A'
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2
求证:△ABC是直角三角形
∴ △ ABC是直角三角形
证明:
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。且边C所对的角为直角。
a2 + b2 = c2
互逆命题
逆定理
定理
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17
例题解析
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
13
A
B
C
D
A
B
C
D
3
4
5
12
例2 一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸如右图所示,这个 零件符合要求吗?
例题解析
B
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
1.
练一练
2、已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
S四边形ABCD=36
中考链接
作业: 1、P76页,第1、4、6题 2《全》P58-59
练一练
3、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
思维训练
1、一个零件的形状如下图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗 四边形ABCD的面积是多少
2、 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.
思维训练
驶向胜利的彼岸
定理与逆定理
开启 智慧
我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.
想一想:
互逆命题与互逆定理有何关系
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.
说出下列命题的逆命题.这些命题的逆命题成立吗
逆命题: 内错角相等,两条直线平行. 成立
逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立
逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立
逆命题:对应角相等的两个三角形是全等三角形. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
试一试
一个命题是真命题,它逆命题却不一定是真命题.
作业: 1、《全》P60
