2021-2022学年人教版数学七年级上册_4.2 线段、直线、射线 课件(共51张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册_4.2 线段、直线、射线 课件(共51张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 08:08:09 | ||
图片预览







文档简介
(共51张PPT)
线段、射线、直线
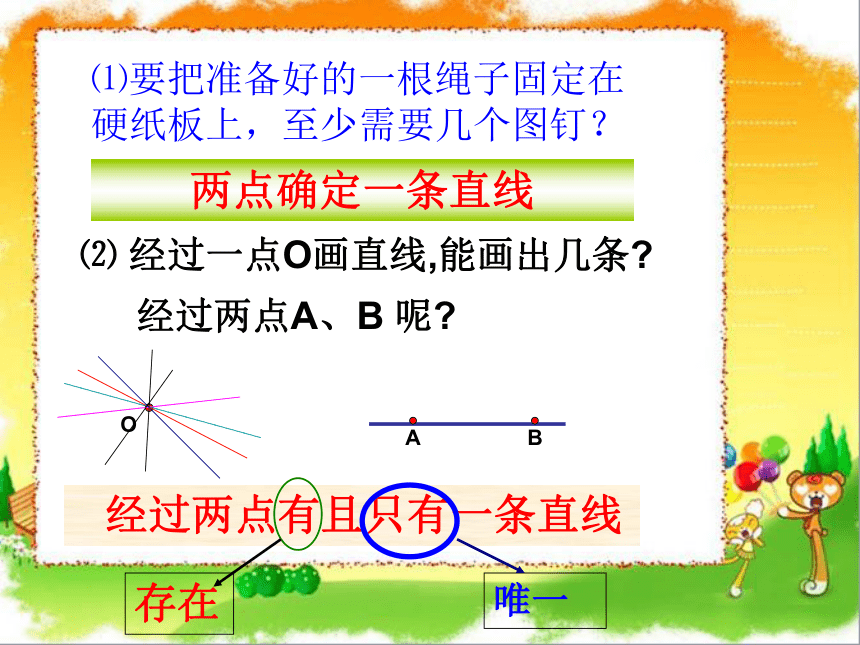
⑴要把准备好的一根绳子固定在 硬纸板上,至少需要几个图钉?
经过两点有且只有一条直线
两点确定一条直线
⑵ 经过一点O画直线,能画出几条
O
经过两点A、B 呢
A
B
存在
唯一
生活中我们常常用到两点确定一条
直线,你能举几个例子吗?
两点确定一条直线的应用:
1.植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
建筑工人在砌墙时经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线, 根据 道理.
两点确定一条直线的
想一想在实际生活中都有哪些地方用到了直线的基本事实呢?
A
B
在我们的日常生活中有哪些有关“直线”形象的例子
点用大写字母表示
点A
怎样用数学符号表示直线
A
B
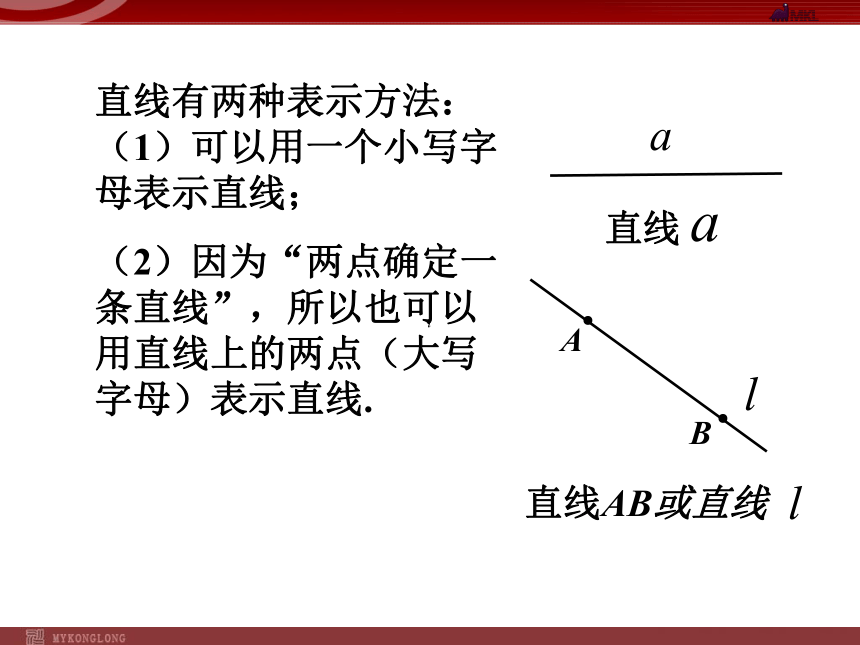
直线有两种表示方法:(1)可以用一个小写字母表示直线;
(2)因为“两点确定一条直线”,所以也可以用直线上的两点(大写字母)表示直线.
●
●
A
B
直线AB或直线
直线
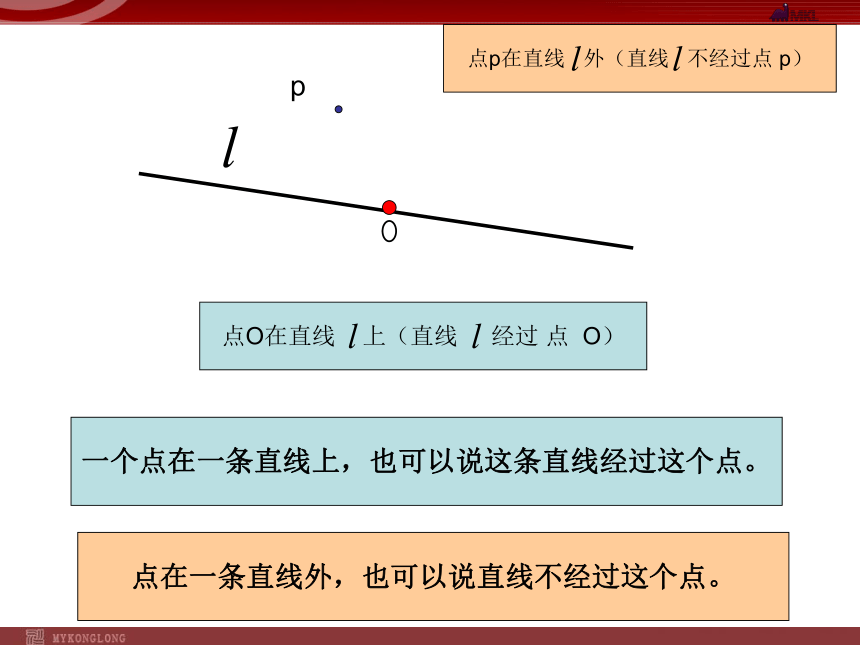
一个点在一条直线上,也可以说这条直线经过这个点。
p
点O在直线 上(直线 经过 点 O)
点在一条直线外,也可以说直线不经过这个点。
点p在直线 外(直线 不经过点 p)
b
a
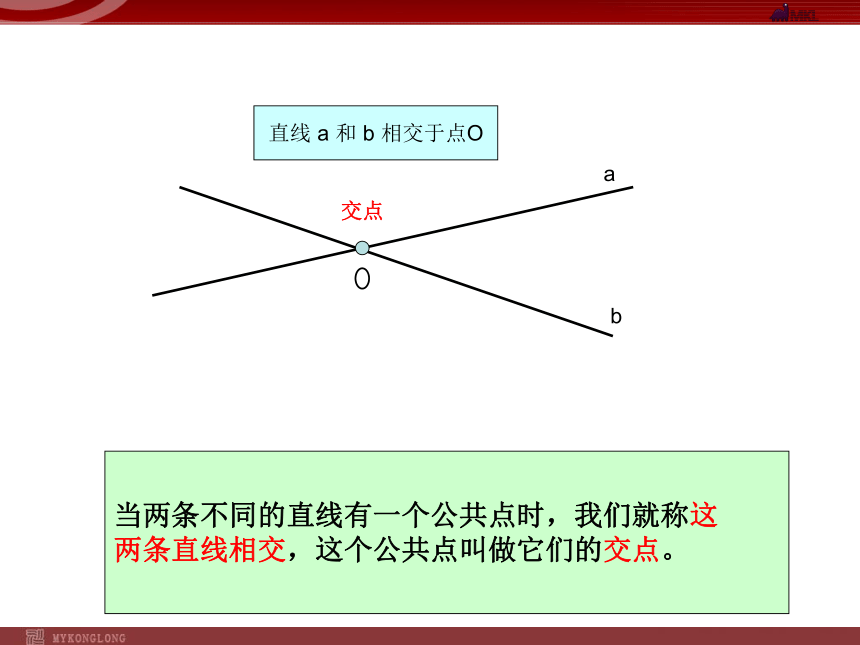
直线 a 和 b 相交于点O
当两条不同的直线有一个公共点时,我们就称这
两条直线相交,这个公共点叫做它们的交点。
交点
(1)点与直线的位置关系:
点在直线上(直线经过点);
点不在直线上(直线不经过点).
(2)当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点.
(1)用恰当的语句描述图中点与直线,直线与直线的关系.
即时练习,巩固新知
P
·
·
Q
l
A
·
A
a
b
c
B
C
(2)按下列语句画出图形:
①直线EF经过点C;
②点A在直线 l 外;
③直线AB与直线CD相交于点A.
即时练习,巩固新知
E
·
·
F
C
·
①
l
A
·
②
③
D
·
·
C
A
B
·
·
在我们的日常生活中有哪些有关“线段”形象的例子
线 段
A
B
线段的表示方法
线段AB (线段BA)
a
或线段a
画一画:画出线段b
b
在我们的日常生活中有哪些有关“射线”形象的例子
射线
射段的表示方法
A
射段OA
O
或射段
画一画:画出射段OB
O
B
怎样用数学符号表示直线、线段、射线
注意问题:(1)线段、直线表示与字母顺序无关
(2)射线表示有方向性,端点在前,射线上任意一点在后
学一学,
议一议
A
B
表示:直线 AB(或直线BA)
表示:直线
A
B
表示:线段 AB(或线段BA)
表示:射线 OA
表示:线段 a
a
表示:射线
O
A
已知线段AB,怎样由线段AB得到射线AB和直线AB呢?
A
B
线段AB
A
B
A
B
射线AB
直线AB
从这一问题你能发现什么呢?
⑴把线段向一个方向无限延伸可
得到射线;
⑵把线段向两个方向延伸可得到直线。
⑶线段和射线都是直线的一部分。
图形 表示方法 端点个数 延伸方向
线段
射线
直线
(2)直线、射线、线段的联系与区别
A
B
a
A
B
a
线段AB或线段a
射线AB或射线a
直线AB或直线a
两个
一个
0
不向任何一方延伸(可度量)
向一方无限延伸(不可度量)
向两方无限延伸(不可度量)
A
B
a
注意:(1)表示线段、射线、直线的时候,都要在字母前 注明“线段” “射线 ” “直线”。
(2)用两个大写字母表示直线或线段时,两个字母可以交换位置,表示射线的两个大写字母不能交换位置,必须把端点字母放在前面。
判断下列说法是否正确:
①线段AB与射线AB都是直线AB的一部分;
②直线AB与直线BA是同一条直线;
③射线AB和射线BA是同一条射线;
④把线段向一个方向无限延伸可得到射线,把线段向两个方向无限延伸可得到直线.
请你把左边对图形的描述和右边相应的图形用线连起来:
连一连
以A为端点,经过点B的射线
连结A,B两点的线段
经过A,B两点的直线
A
B
A
A
B
B
练习
按下列语句画出图形:
(1)直线EF经过点C;
(2) 点A在直线 外
(3)经过点O的三条线段a、b、c;
(4)线段AB、CD相交于点B
C
E
F
(1)
(2)
A
(3)
a
b
c
(4)
A
B
C
D
如图,已知三点A、B、C.
(1)画直线AB;
(2)画射线AC;
(3)连接BC.
B
A
C
请分别表示出下图中线段、射线、直线.
A
B
C
答:
有3条线段,是线段 AB、线段 AC、线段 BC
有6条射线,分别是每个点分成的两条.
只有一条直线,是直线 AB
做一做
A
B
C
D
答:有1条直线,8条射线,6条线段。
下图中,有几条直线,几条射线,几条线段?
说一说,这节课
你有什么收获
两点确定一条直线
经过两点有且只有一条直线
用数学符号表示直线、
射线、线段
当堂检测,查漏补缺
1、下列关于直线的表示方法正确地是( )
A B C D
2、上完数学课后,晚上小明拿起手电筒射向远方,高兴地说这是一条( )
A. 线段 B. 射线 C. 直线 D. 不能确定
3、如图所示,下列说法正确的是 ( )
A. 射线AB B. 延长线段AB
C. 延长线段B A D. 反向延长线段B A
4、植树时,至少要定出________个树坑的位置,才能确定同一行树坑在同一直线上,其中的数学道理是_______________________ .
C
B
C
2
两点确定一条直线
5、如图,射线PA与PB是同一条射线,则符合题意的图为( )
P
A
B
P
P
P
P
A
A
A
B
B
B
A
B
C
D
答案:
6、如图所示的直线、射线、线段能相交的是( )
A
B
B
A
A
A
C
B
B
A
B
C
D
C
C
C
D
D
D
D
答案:
课堂小结,课外延伸
思考题:
往返于A、B两地的客车,中途停靠三个站,每两站间的票价均不相同,
问:(1)有多少种不同的票价?
(2)要准备多少种车票?
练习
读下列语句,并分别画出图形:
(1)直线 经过A、B、C三点,
并且点C在点A与B之间;
(2)两条线段m与n相交于点P;
(3) p是直线外一点,过点p有一条
直线b与直线a相交于点Q;
(4)直线 、 、 相交于点Q。
B
A
C
m
n
p
p
Q
a
b
Q
m
n
直线的基本性质:
经过两点有且只有一条直线
存在性
唯一性
即:两点确定一条直线
(2)经过一个已知点画直线,可以
画多少条?
(3)经过两个已知点画直线,可
以画多少条?
(1)如果你想将一根细木条固
定在墙上,至少需要几个钉子?
自学反馈(一)
自学反馈(一)
(4 )平面内三点可确定 条直线.
(5)种树时,只要定出两个树坑的位置,就能确定同一行的树所在的直线,这是因为 。
请你把左边对图形的描述和右边相应的图形用线连起来:
连一连
以A为端点,经过点B的射线
连结A,B两点的线段
经过A,B两点的直线
线段、射线、直线的表示方法
A
B
线段 AB(或线段BA)
a
线段 a
线段: (1)用表示端点的两个大写字母表示
(2)用一个小写字母表示
O
射线 OA(不能记作AO)
直线 AB(或直线BA)
直线 a
直线: (1)用它上面任意两点的大写字母表示
(2)用一个小写字母表示
射线:用它的端点和射线方向上的另外任意一点的两个大写字母表示
A
A
B
a
1.下列给线段取名正确的是:( )
(A)线段M (B)线段m
(C )线段Mn (D)线段mn
B
2.如图,若射线AB上有一点C,下列与射线AB是同一条射线的是( )
(A)射线BA (B)射线AC
(C )射线BC (D)射线CB
A B C
B
自学反馈(二)
3.图中的几何体有多少条棱?请写出这些表示棱的线段。
4.请写出图中以O为端点的各条射线。
5.用两种方式表示图中的两条直线。
o
A
B
第一种:直线 AO,
直线 BO
第二种:直线 m ,
直线 n
探究练习:
已知线段AB,你能由线段AB得到射线和直线吗?动手试一试
A
B
A
B
A
B
A
B
答案
例:按下列语句画图
1、已知A 、B、 C、D四个点
(1)画直线AB
(2)画射线AC
(3)连结 DC
2、线段a b相交于点O.
3、点A在直线l外
C
B
A
D
O
a
b
L
A
1、判断
(1)延长直线MN到点C ( )
(2)直线A与直线B交于一点M ( )
(3)三点决定一条直线 ( )
(4)无数条直线可能交于一点 ( )
错
错
错
对
当堂检测
2、下图(1)中的线段可表示为 或 。
(2)中的直线可表示为 或 。
(3)中的射线可表示为 。
3、按下列语句画出图形
(1)直线EF经过点C (2)点A在直线L外
(3)经过点O的三条线段a、b、c (4)线段AB、CD相交于点B
4、用适当的语言描述下列图
E
H
F
E
n
B
A
m
Q
P
N
M
O
D
C
B
A
线段AB
线段m
直线EF
直线n
射线HE
选做题:
1、如图线段AB上有两点C、 D则共有几条线段?
2、变形题:往返于甲乙两地的客车中途要停靠三个车站,有多少种不同的票价?要准备多少种不同的车票?
A
B
C
D
线段、射线、直线
⑴要把准备好的一根绳子固定在 硬纸板上,至少需要几个图钉?
经过两点有且只有一条直线
两点确定一条直线
⑵ 经过一点O画直线,能画出几条
O
经过两点A、B 呢
A
B
存在
唯一
生活中我们常常用到两点确定一条
直线,你能举几个例子吗?
两点确定一条直线的应用:
1.植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
建筑工人在砌墙时经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线, 根据 道理.
两点确定一条直线的
想一想在实际生活中都有哪些地方用到了直线的基本事实呢?
A
B
在我们的日常生活中有哪些有关“直线”形象的例子
点用大写字母表示
点A
怎样用数学符号表示直线
A
B
直线有两种表示方法:(1)可以用一个小写字母表示直线;
(2)因为“两点确定一条直线”,所以也可以用直线上的两点(大写字母)表示直线.
●
●
A
B
直线AB或直线
直线
一个点在一条直线上,也可以说这条直线经过这个点。
p
点O在直线 上(直线 经过 点 O)
点在一条直线外,也可以说直线不经过这个点。
点p在直线 外(直线 不经过点 p)
b
a
直线 a 和 b 相交于点O
当两条不同的直线有一个公共点时,我们就称这
两条直线相交,这个公共点叫做它们的交点。
交点
(1)点与直线的位置关系:
点在直线上(直线经过点);
点不在直线上(直线不经过点).
(2)当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点.
(1)用恰当的语句描述图中点与直线,直线与直线的关系.
即时练习,巩固新知
P
·
·
Q
l
A
·
A
a
b
c
B
C
(2)按下列语句画出图形:
①直线EF经过点C;
②点A在直线 l 外;
③直线AB与直线CD相交于点A.
即时练习,巩固新知
E
·
·
F
C
·
①
l
A
·
②
③
D
·
·
C
A
B
·
·
在我们的日常生活中有哪些有关“线段”形象的例子
线 段
A
B
线段的表示方法
线段AB (线段BA)
a
或线段a
画一画:画出线段b
b
在我们的日常生活中有哪些有关“射线”形象的例子
射线
射段的表示方法
A
射段OA
O
或射段
画一画:画出射段OB
O
B
怎样用数学符号表示直线、线段、射线
注意问题:(1)线段、直线表示与字母顺序无关
(2)射线表示有方向性,端点在前,射线上任意一点在后
学一学,
议一议
A
B
表示:直线 AB(或直线BA)
表示:直线
A
B
表示:线段 AB(或线段BA)
表示:射线 OA
表示:线段 a
a
表示:射线
O
A
已知线段AB,怎样由线段AB得到射线AB和直线AB呢?
A
B
线段AB
A
B
A
B
射线AB
直线AB
从这一问题你能发现什么呢?
⑴把线段向一个方向无限延伸可
得到射线;
⑵把线段向两个方向延伸可得到直线。
⑶线段和射线都是直线的一部分。
图形 表示方法 端点个数 延伸方向
线段
射线
直线
(2)直线、射线、线段的联系与区别
A
B
a
A
B
a
线段AB或线段a
射线AB或射线a
直线AB或直线a
两个
一个
0
不向任何一方延伸(可度量)
向一方无限延伸(不可度量)
向两方无限延伸(不可度量)
A
B
a
注意:(1)表示线段、射线、直线的时候,都要在字母前 注明“线段” “射线 ” “直线”。
(2)用两个大写字母表示直线或线段时,两个字母可以交换位置,表示射线的两个大写字母不能交换位置,必须把端点字母放在前面。
判断下列说法是否正确:
①线段AB与射线AB都是直线AB的一部分;
②直线AB与直线BA是同一条直线;
③射线AB和射线BA是同一条射线;
④把线段向一个方向无限延伸可得到射线,把线段向两个方向无限延伸可得到直线.
请你把左边对图形的描述和右边相应的图形用线连起来:
连一连
以A为端点,经过点B的射线
连结A,B两点的线段
经过A,B两点的直线
A
B
A
A
B
B
练习
按下列语句画出图形:
(1)直线EF经过点C;
(2) 点A在直线 外
(3)经过点O的三条线段a、b、c;
(4)线段AB、CD相交于点B
C
E
F
(1)
(2)
A
(3)
a
b
c
(4)
A
B
C
D
如图,已知三点A、B、C.
(1)画直线AB;
(2)画射线AC;
(3)连接BC.
B
A
C
请分别表示出下图中线段、射线、直线.
A
B
C
答:
有3条线段,是线段 AB、线段 AC、线段 BC
有6条射线,分别是每个点分成的两条.
只有一条直线,是直线 AB
做一做
A
B
C
D
答:有1条直线,8条射线,6条线段。
下图中,有几条直线,几条射线,几条线段?
说一说,这节课
你有什么收获
两点确定一条直线
经过两点有且只有一条直线
用数学符号表示直线、
射线、线段
当堂检测,查漏补缺
1、下列关于直线的表示方法正确地是( )
A B C D
2、上完数学课后,晚上小明拿起手电筒射向远方,高兴地说这是一条( )
A. 线段 B. 射线 C. 直线 D. 不能确定
3、如图所示,下列说法正确的是 ( )
A. 射线AB B. 延长线段AB
C. 延长线段B A D. 反向延长线段B A
4、植树时,至少要定出________个树坑的位置,才能确定同一行树坑在同一直线上,其中的数学道理是_______________________ .
C
B
C
2
两点确定一条直线
5、如图,射线PA与PB是同一条射线,则符合题意的图为( )
P
A
B
P
P
P
P
A
A
A
B
B
B
A
B
C
D
答案:
6、如图所示的直线、射线、线段能相交的是( )
A
B
B
A
A
A
C
B
B
A
B
C
D
C
C
C
D
D
D
D
答案:
课堂小结,课外延伸
思考题:
往返于A、B两地的客车,中途停靠三个站,每两站间的票价均不相同,
问:(1)有多少种不同的票价?
(2)要准备多少种车票?
练习
读下列语句,并分别画出图形:
(1)直线 经过A、B、C三点,
并且点C在点A与B之间;
(2)两条线段m与n相交于点P;
(3) p是直线外一点,过点p有一条
直线b与直线a相交于点Q;
(4)直线 、 、 相交于点Q。
B
A
C
m
n
p
p
Q
a
b
Q
m
n
直线的基本性质:
经过两点有且只有一条直线
存在性
唯一性
即:两点确定一条直线
(2)经过一个已知点画直线,可以
画多少条?
(3)经过两个已知点画直线,可
以画多少条?
(1)如果你想将一根细木条固
定在墙上,至少需要几个钉子?
自学反馈(一)
自学反馈(一)
(4 )平面内三点可确定 条直线.
(5)种树时,只要定出两个树坑的位置,就能确定同一行的树所在的直线,这是因为 。
请你把左边对图形的描述和右边相应的图形用线连起来:
连一连
以A为端点,经过点B的射线
连结A,B两点的线段
经过A,B两点的直线
线段、射线、直线的表示方法
A
B
线段 AB(或线段BA)
a
线段 a
线段: (1)用表示端点的两个大写字母表示
(2)用一个小写字母表示
O
射线 OA(不能记作AO)
直线 AB(或直线BA)
直线 a
直线: (1)用它上面任意两点的大写字母表示
(2)用一个小写字母表示
射线:用它的端点和射线方向上的另外任意一点的两个大写字母表示
A
A
B
a
1.下列给线段取名正确的是:( )
(A)线段M (B)线段m
(C )线段Mn (D)线段mn
B
2.如图,若射线AB上有一点C,下列与射线AB是同一条射线的是( )
(A)射线BA (B)射线AC
(C )射线BC (D)射线CB
A B C
B
自学反馈(二)
3.图中的几何体有多少条棱?请写出这些表示棱的线段。
4.请写出图中以O为端点的各条射线。
5.用两种方式表示图中的两条直线。
o
A
B
第一种:直线 AO,
直线 BO
第二种:直线 m ,
直线 n
探究练习:
已知线段AB,你能由线段AB得到射线和直线吗?动手试一试
A
B
A
B
A
B
A
B
答案
例:按下列语句画图
1、已知A 、B、 C、D四个点
(1)画直线AB
(2)画射线AC
(3)连结 DC
2、线段a b相交于点O.
3、点A在直线l外
C
B
A
D
O
a
b
L
A
1、判断
(1)延长直线MN到点C ( )
(2)直线A与直线B交于一点M ( )
(3)三点决定一条直线 ( )
(4)无数条直线可能交于一点 ( )
错
错
错
对
当堂检测
2、下图(1)中的线段可表示为 或 。
(2)中的直线可表示为 或 。
(3)中的射线可表示为 。
3、按下列语句画出图形
(1)直线EF经过点C (2)点A在直线L外
(3)经过点O的三条线段a、b、c (4)线段AB、CD相交于点B
4、用适当的语言描述下列图
E
H
F
E
n
B
A
m
Q
P
N
M
O
D
C
B
A
线段AB
线段m
直线EF
直线n
射线HE
选做题:
1、如图线段AB上有两点C、 D则共有几条线段?
2、变形题:往返于甲乙两地的客车中途要停靠三个车站,有多少种不同的票价?要准备多少种不同的车票?
A
B
C
D
