2021-2022学年湘教版数学八年级上册4.2.1不等式的基本性质1 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级上册4.2.1不等式的基本性质1 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
不等式的基本性质1
哦!真的吗?是真的吗
“哈哈哈!
爸爸,我发现个秘密:你比我大30岁,30年后,我的年龄就可以追上你,那时,我们两个一样大!
思考1:30年后,大头儿子是否和小头爸爸的年龄一样大?
思考2:你会用数学式子写出理由吗?
一、情况导入,遇问题
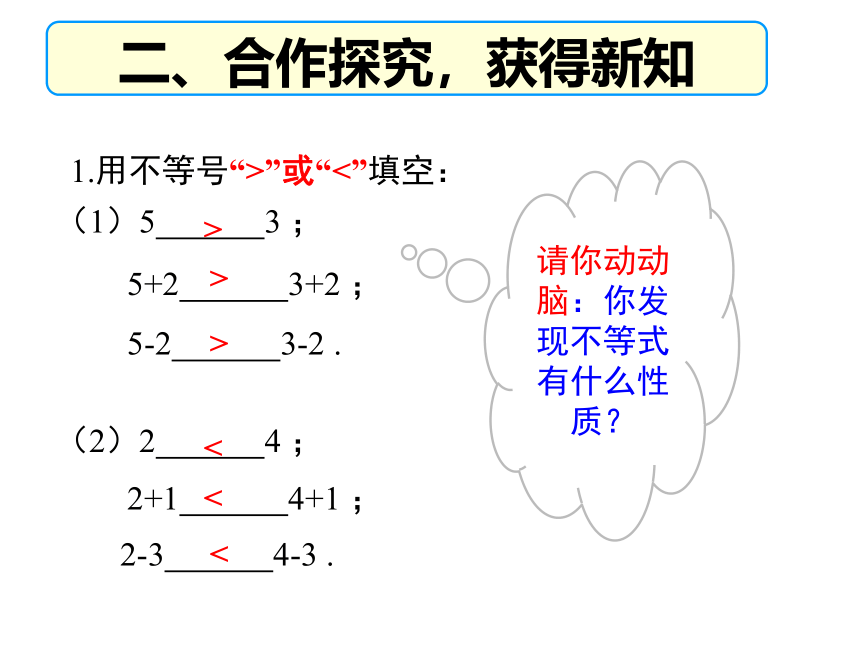
1.用不等号“>”或“<”填空:
(1)5 3 ;
5+2 3+2 ;
5-2 3-2 .
(2)2 4 ;
2+1 4+1 ;
2-3 4-3 .
>
>
>
<
<
<
二、合作探究,获得新知
请你动动脑:你发现不等式有什么性质?
请你动动脑:你发现不等式有什么性质?
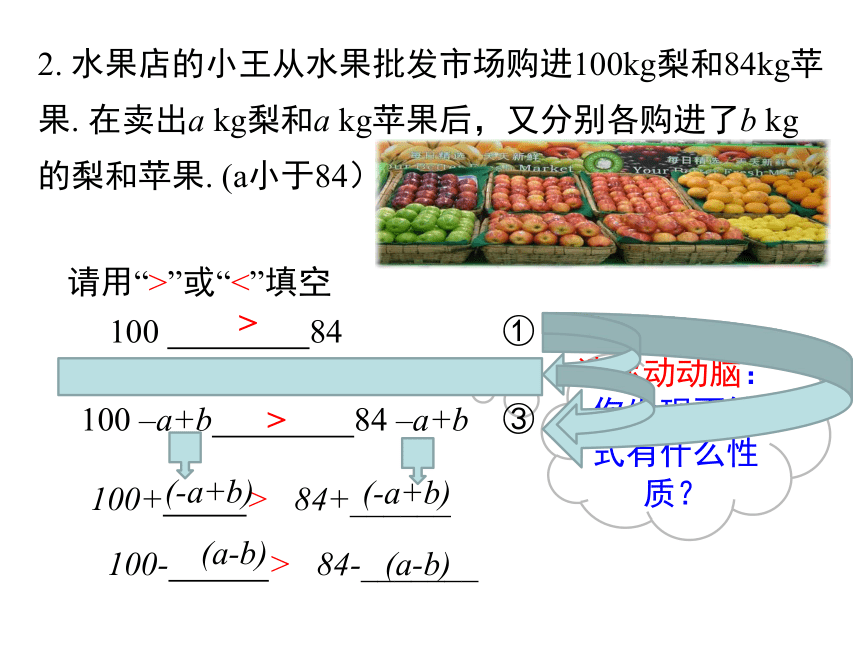
100 -a 84 -a ②
>
请用“>”或“<”填空
100 –a+b 84 –a+b ③
>
100 84 ①
>
100+ > 84+______
100- > 84-_______
(-a+b)
(-a+b)
(a-b)
(a-b)
2. 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果. (a小于84)
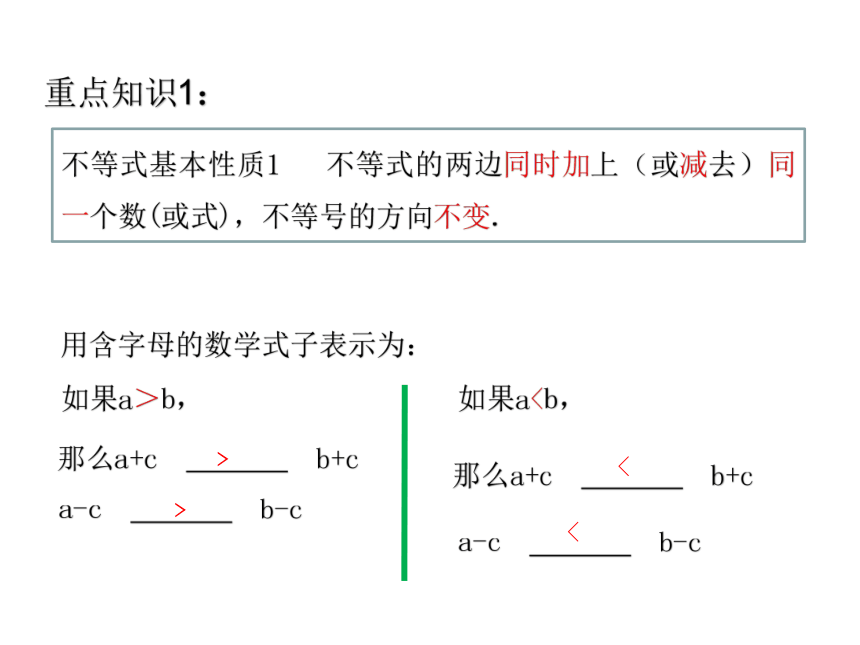
不等式基本性质1 不等式的两边同时加上(或减去)同一个数(或式),不等号的方向不变.
用含字母的数学式子表示为:
那么a+c b+c
重点知识1:
﹥
a-c b-c
﹥
如果a>b,
如果a那么a+c b+c
<
a-c b-c
<
不等式基本性质1 不等式的两边同时加上(或减去)同一个数(或式),不等号的方向不变.
重点知识1:
不等式的基本性质1的三个特征:两同一不变
(1)同加减(运算符号相同);
(2)同一个数(加数或减数相同);
(3)不等号的方向不变。
(1)已知 a>b,则a+3 b+3,理由是:
————————————
>
例1 填空:
三、例题讲解,熟悉新知
根据不等式的基本性质1,在不等式的两边同时上3,
不等号的方向不变。
(2)已知 a≤b,则a-c b-c,理由是:
——————————
≤
根据不等式的基本性质1,在不等式的两边同时减去c,不等号的方向不变。
*例2 填空:
(1)已知 a————————————
(2)已知 a<
>
根据不等式的基本性质1,在不等式的两边同时加上 ,不等号的方向不变。
根据不等式的基本性质1,在不等式的两边先减去5,再加上c,不等号的方向不变。
根据不等式的基本性质1,在不等式的两边同时减去 ,不等号的方向不变。
(-5+c)
(5-c)
(1) x + 6 > 5,
解: x +6-6 > 5-6,
x > -1.
(2) 3x < 2x -2,
**例3:利用不等式的基本性质1,把下列不等式化为x >a或x< a的形式:
(1)x + 6 > 5 ;
(2) 3x < 2x -2 .
解:
x > 5-6,
x > -1.
解:
3x -2x < -2, x < -2.
解:3x -2x < 2x -2-2x,
x < -2.
3x < 2x -2
3x-2x < -2
把不等式一边的某一项变号后移到另一边,这种变形叫做移项.
重点2:移项要变号
*1、利用移项法把下列不等式化成为x >a或x< a的形式:
(1)若x+3>6,则_____ ,
(2)若a-2<3,则______,
(3)若2y+2<y+3,则______,
(4)若-6x+5>3-7x,则_____ ,
a<5
x>3
y<1
x>-2
四:小题练习,巩固新知
**2、下列不等式的变形正确的是( )
A. 由 3x < 2x - 2,得 x >-2
B. 由3x +1>2x -1 ,得 x > 2
C. 由 2x + 1> x -1 ,得 x <- 2
D. 由 3x +2 < 2x - 2,得 x < -4
D
难点:移项只改变移动的项的符号,没有移动的项的符号不变,且不等号的方向保持不变.
“哈哈哈!
爸爸,我发现个秘密:你比我大30岁,30年后,我的年龄就可以追上你,那时,我们两个一样大!
哦!真的吗?是真的吗
思考1:30年后,大头儿子是否和小头爸爸的年龄一样大?
思考2:你会用数学式子写出理由吗?
***3、实际应用,解决问题
****思考题:已知一个三角形的三边长分别为:8,9,x。则整数x的值有 个。
五、难度升级,挑战自我!
15
(1)重点1:不等式基本性质1
不等式的两边同时加上(或减去)同一个数(或式),不等号的方向不变。
(2)重点2:移项要变号。
六:课堂小结
P137:A组1,2
七、作业
感谢聆听
不等式的基本性质1
哦!真的吗?是真的吗
“哈哈哈!
爸爸,我发现个秘密:你比我大30岁,30年后,我的年龄就可以追上你,那时,我们两个一样大!
思考1:30年后,大头儿子是否和小头爸爸的年龄一样大?
思考2:你会用数学式子写出理由吗?
一、情况导入,遇问题
1.用不等号“>”或“<”填空:
(1)5 3 ;
5+2 3+2 ;
5-2 3-2 .
(2)2 4 ;
2+1 4+1 ;
2-3 4-3 .
>
>
>
<
<
<
二、合作探究,获得新知
请你动动脑:你发现不等式有什么性质?
请你动动脑:你发现不等式有什么性质?
100 -a 84 -a ②
>
请用“>”或“<”填空
100 –a+b 84 –a+b ③
>
100 84 ①
>
100+ > 84+______
100- > 84-_______
(-a+b)
(-a+b)
(a-b)
(a-b)
2. 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果. (a小于84)
不等式基本性质1 不等式的两边同时加上(或减去)同一个数(或式),不等号的方向不变.
用含字母的数学式子表示为:
那么a+c b+c
重点知识1:
﹥
a-c b-c
﹥
如果a>b,
如果a
<
a-c b-c
<
不等式基本性质1 不等式的两边同时加上(或减去)同一个数(或式),不等号的方向不变.
重点知识1:
不等式的基本性质1的三个特征:两同一不变
(1)同加减(运算符号相同);
(2)同一个数(加数或减数相同);
(3)不等号的方向不变。
(1)已知 a>b,则a+3 b+3,理由是:
————————————
>
例1 填空:
三、例题讲解,熟悉新知
根据不等式的基本性质1,在不等式的两边同时上3,
不等号的方向不变。
(2)已知 a≤b,则a-c b-c,理由是:
——————————
≤
根据不等式的基本性质1,在不等式的两边同时减去c,不等号的方向不变。
*例2 填空:
(1)已知 a
(2)已知 a
>
根据不等式的基本性质1,在不等式的两边同时加上 ,不等号的方向不变。
根据不等式的基本性质1,在不等式的两边先减去5,再加上c,不等号的方向不变。
根据不等式的基本性质1,在不等式的两边同时减去 ,不等号的方向不变。
(-5+c)
(5-c)
(1) x + 6 > 5,
解: x +6-6 > 5-6,
x > -1.
(2) 3x < 2x -2,
**例3:利用不等式的基本性质1,把下列不等式化为x >a或x< a的形式:
(1)x + 6 > 5 ;
(2) 3x < 2x -2 .
解:
x > 5-6,
x > -1.
解:
3x -2x < -2, x < -2.
解:3x -2x < 2x -2-2x,
x < -2.
3x < 2x -2
3x-2x < -2
把不等式一边的某一项变号后移到另一边,这种变形叫做移项.
重点2:移项要变号
*1、利用移项法把下列不等式化成为x >a或x< a的形式:
(1)若x+3>6,则_____ ,
(2)若a-2<3,则______,
(3)若2y+2<y+3,则______,
(4)若-6x+5>3-7x,则_____ ,
a<5
x>3
y<1
x>-2
四:小题练习,巩固新知
**2、下列不等式的变形正确的是( )
A. 由 3x < 2x - 2,得 x >-2
B. 由3x +1>2x -1 ,得 x > 2
C. 由 2x + 1> x -1 ,得 x <- 2
D. 由 3x +2 < 2x - 2,得 x < -4
D
难点:移项只改变移动的项的符号,没有移动的项的符号不变,且不等号的方向保持不变.
“哈哈哈!
爸爸,我发现个秘密:你比我大30岁,30年后,我的年龄就可以追上你,那时,我们两个一样大!
哦!真的吗?是真的吗
思考1:30年后,大头儿子是否和小头爸爸的年龄一样大?
思考2:你会用数学式子写出理由吗?
***3、实际应用,解决问题
****思考题:已知一个三角形的三边长分别为:8,9,x。则整数x的值有 个。
五、难度升级,挑战自我!
15
(1)重点1:不等式基本性质1
不等式的两边同时加上(或减去)同一个数(或式),不等号的方向不变。
(2)重点2:移项要变号。
六:课堂小结
P137:A组1,2
七、作业
感谢聆听
同课章节目录
