2021-2022七上第四章 实数 4.2平方根(2)课件(共19张PPT)
文档属性
| 名称 | 2021-2022七上第四章 实数 4.2平方根(2)课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 632.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 08:38:27 | ||
图片预览






文档简介
(共19张PPT)
4.2 平方根(2)
1.了解平方根的概念,会用根号表示一个正数的平方根,并进行相关的计算.
2.了解开方和乘方是互逆运算,会利用这个互逆运算求某些非负数的平方根.
学习目标
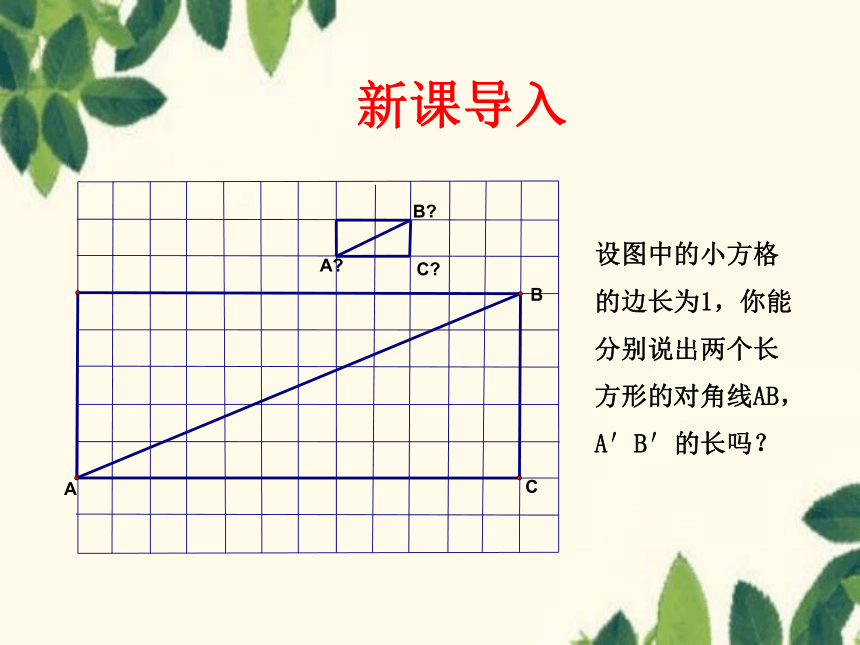
设图中的小方格的边长为1,你能分别说出两个长方形的对角线AB,A′B′的长吗?
C
B
A
C
B
A
新课导入
想一想:
如果一个数的平方等于9,那么这个数是多少?
3和-3的平方都等于9
填一填:写出左圈和右圈中的“?”表示的数:
64
-11
11
0.6
0
没有
x
2
x
8
-8
4
3
4
3
-
121
0.36
0
-4
-0.6
一般地,如果一个数x的平方等于a,即x2=a,那么这个数x就叫做a的平方根(或二次方根).
例如,因为3和-3的平方都等于9,我们就说3和-3是9的平方根.也可以说9的平方根是±3.
平方根的定义:
定义:
知识讲解
平方根的表示方法、读法
根号
被开方数
(a是非负数)
读作:正、负根号a
(1)一个正数有几个平方根?
(2)0 有几个平方根?
(3)负数呢?
一个正数有两个平方根,它们互为相反数;
0只有一个平方根,它是0本身;
负数没有平方根.
议一议
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9
x x2
1
4
9
+1
-1
+2
-2
+3
-3
这是什么运算?
平方运算
x2 x
求一个数a的平方根的运算,叫做开平方,a叫做被开方数.
可以看出,平方与开平方互为逆运算,根据这种关系可以求出一个数的平方根.
平方与开平方有什么关系?
开平方的定义:
定义:
【例】求下列各数的平方根:
(1)25 (2)0.81 (3)15
(4)(-2) (5)0 (6)-3
【例题】
【解析】(1)因为 ,所以25的平方根是±5,即
(2)因为 ,所以0.81的平方根是±0.9,即
(3)15的平方根是±
(4)因为 ,所以 的平方根是±2,即
(5)0的平方根是0.
(6)-3没有平方根.
1.一个数的平方等于它本身,这个数是________,
一个数的平方根等于它本身,这个数是________.
2.若3a+1的平方根是0,那么a一定是______.
3. 若4a+1的平方根是±5,则a=______.
1, 0
0
6
【跟踪训练】
1.(杭州·中考)4的平方根是 ( )
A. 2 B. 2 C. 16 D. 16
【解析】选B.4的平方根是 = 2.
随堂练习
2.(黄冈·中考)2的平方根是_________.
【解析】根据平方根的定义得出2的平方根是± .
答案:±
3.一个数x的平方根等于m+1和m-3,则m= ,x= .
【解析】根据一个正数的平方根互为相反数得,m+1和
m-3互为相反数,即m+1+m-3=0,解得m=1,则m+1=2,
m-3=-2,所以x=4.
答案:1 4
4.若|a-9|+(b-4) =0,则 的平方根是____.
【解析】因为|a-9|和(b-4) 都是非负数,且|a-9|+
(b-4) =0,所以|a-9|=0,(b-4) =0,所以a=9,b=4,
,其平方根为
答案:
5.求下列各式中的x:
(1) x =16 (2) x =
(3) x =15 (4) 4x =81
【解析】
通过本课时的学习,需要我们掌握:
1.平方根的定义:
一般地,如果一个数x的平方等于a,即x2=a,
那么这个数x就叫做a的平方根(或二次方根).
2.开平方的定义:
求一个数a的平方根的运算,叫做开平方.
课堂小结
4.2 平方根(2)
1.了解平方根的概念,会用根号表示一个正数的平方根,并进行相关的计算.
2.了解开方和乘方是互逆运算,会利用这个互逆运算求某些非负数的平方根.
学习目标
设图中的小方格的边长为1,你能分别说出两个长方形的对角线AB,A′B′的长吗?
C
B
A
C
B
A
新课导入
想一想:
如果一个数的平方等于9,那么这个数是多少?
3和-3的平方都等于9
填一填:写出左圈和右圈中的“?”表示的数:
64
-11
11
0.6
0
没有
x
2
x
8
-8
4
3
4
3
-
121
0.36
0
-4
-0.6
一般地,如果一个数x的平方等于a,即x2=a,那么这个数x就叫做a的平方根(或二次方根).
例如,因为3和-3的平方都等于9,我们就说3和-3是9的平方根.也可以说9的平方根是±3.
平方根的定义:
定义:
知识讲解
平方根的表示方法、读法
根号
被开方数
(a是非负数)
读作:正、负根号a
(1)一个正数有几个平方根?
(2)0 有几个平方根?
(3)负数呢?
一个正数有两个平方根,它们互为相反数;
0只有一个平方根,它是0本身;
负数没有平方根.
议一议
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9
x x2
1
4
9
+1
-1
+2
-2
+3
-3
这是什么运算?
平方运算
x2 x
求一个数a的平方根的运算,叫做开平方,a叫做被开方数.
可以看出,平方与开平方互为逆运算,根据这种关系可以求出一个数的平方根.
平方与开平方有什么关系?
开平方的定义:
定义:
【例】求下列各数的平方根:
(1)25 (2)0.81 (3)15
(4)(-2) (5)0 (6)-3
【例题】
【解析】(1)因为 ,所以25的平方根是±5,即
(2)因为 ,所以0.81的平方根是±0.9,即
(3)15的平方根是±
(4)因为 ,所以 的平方根是±2,即
(5)0的平方根是0.
(6)-3没有平方根.
1.一个数的平方等于它本身,这个数是________,
一个数的平方根等于它本身,这个数是________.
2.若3a+1的平方根是0,那么a一定是______.
3. 若4a+1的平方根是±5,则a=______.
1, 0
0
6
【跟踪训练】
1.(杭州·中考)4的平方根是 ( )
A. 2 B. 2 C. 16 D. 16
【解析】选B.4的平方根是 = 2.
随堂练习
2.(黄冈·中考)2的平方根是_________.
【解析】根据平方根的定义得出2的平方根是± .
答案:±
3.一个数x的平方根等于m+1和m-3,则m= ,x= .
【解析】根据一个正数的平方根互为相反数得,m+1和
m-3互为相反数,即m+1+m-3=0,解得m=1,则m+1=2,
m-3=-2,所以x=4.
答案:1 4
4.若|a-9|+(b-4) =0,则 的平方根是____.
【解析】因为|a-9|和(b-4) 都是非负数,且|a-9|+
(b-4) =0,所以|a-9|=0,(b-4) =0,所以a=9,b=4,
,其平方根为
答案:
5.求下列各式中的x:
(1) x =16 (2) x =
(3) x =15 (4) 4x =81
【解析】
通过本课时的学习,需要我们掌握:
1.平方根的定义:
一般地,如果一个数x的平方等于a,即x2=a,
那么这个数x就叫做a的平方根(或二次方根).
2.开平方的定义:
求一个数a的平方根的运算,叫做开平方.
课堂小结
