2021-2022七上第一章 三角形1.1认识三角形(4)课件(共16张PPT)
文档属性
| 名称 | 2021-2022七上第一章 三角形1.1认识三角形(4)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 245.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1.1认识三角形(4)
如图,用铅笔可以支起一张均匀的三角形卡片,你知道怎样确定这个支撑点的位置吗?
情景导入
教学 目 标
1、了解三角形的中线、角平分线及相关性质,并能熟悉的画出这两条线段。
2、能应用三角形的中线、角平分线的性质解决简单的数学问题题。
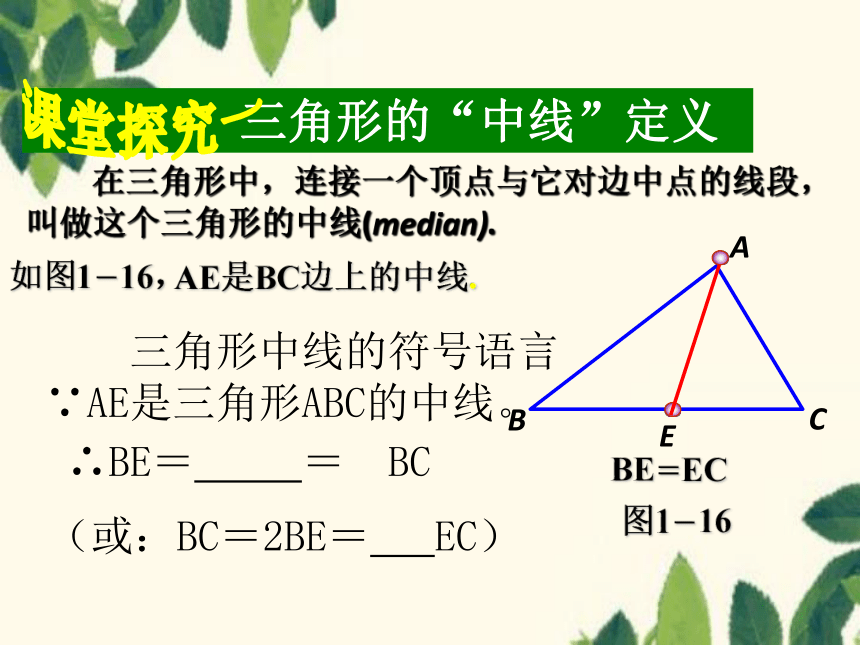
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线(median).
三角形的“中线”定义
BE=EC
图1 16
B
C
E
A
如图1 16,
AE是BC边上的中线.
课堂探究一
(或:BC=2BE= EC)
∴BE= = BC
三角形中线的符号语言
∵AE是三角形ABC的中线。
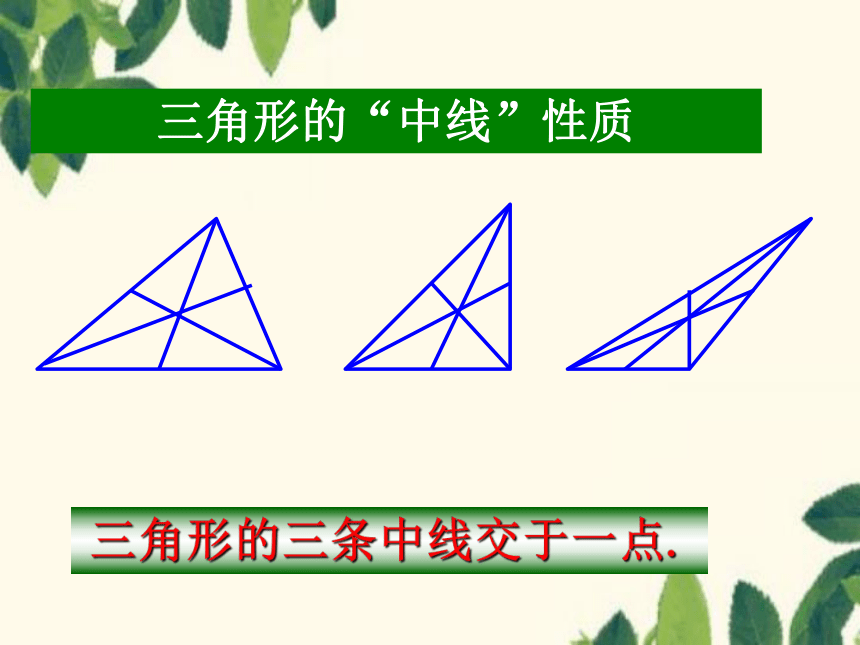
探究三角形的“中线”性质
B
C
E
A
(1) 在纸上画出一个锐角三角形 ,并画出它的三条中线.
议一议
它们有怎样的位置关系
与同伴进行交流.
(2) 钝角三角形和直角三角形的三条中线
也有同样的位置关系吗
三角形的三条中线交于一点.
三角形的“中线”性质
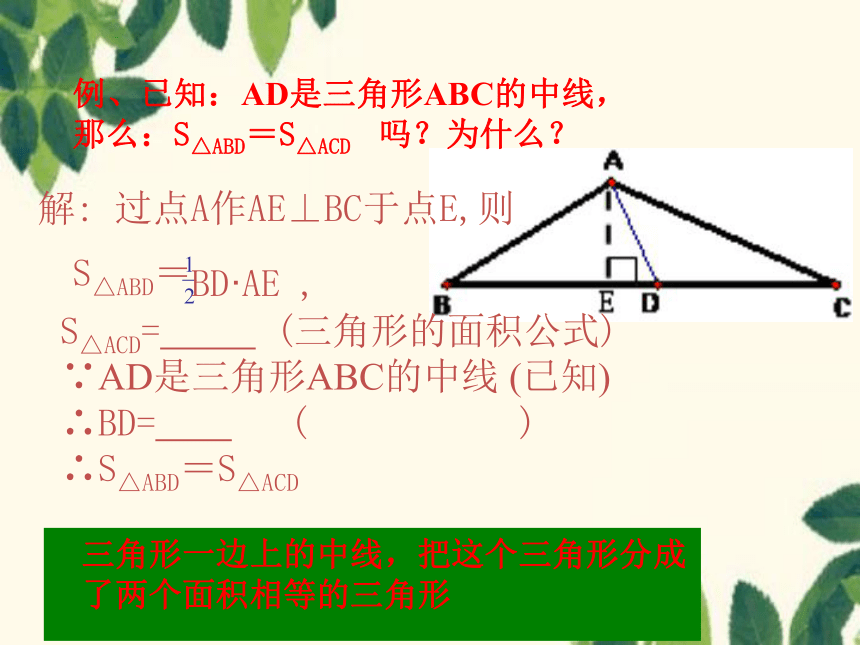
三角形一边上的中线,把这个三角形分成
了两个面积相等的三角形
例、已知:AD是三角形ABC的中线,
那么:S△ABD=S△ACD 吗?为什么?
S△ACD= (三角形的面积公式)
∵AD是三角形ABC的中线 (已知)
∴BD= ( )
∴S△ABD=S△ACD
BD·AE ,
解: 过点A作AE⊥BC于点E,则
S△ABD=
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗
B
A
C
你能通过折纸的方法得到它吗
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A
的角平分线.
A
B
C
A
D
课堂探究二
D
三角形的角平分线的定义
以前所学的“角平分线”是一条射线,
B
A
C
“三角形的角平分线”
还是射线 吗
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的
线段叫三角形的角平分线.
线段
“三角形的角平分线”是一条线段.
!
D
∠1=∠2
1
2
三角形的角平分线的性质
每人准备锐角三角形、钝角三角形和直角三角形纸片各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗
(2) 你能用折纸的办法得到它们吗
(3) 在每个三角形中,这三条角平分线之间有怎样的
位置关系
将你的结果与同伴进行交流.
三角形的三条角平分线交于同一点.
1. (1)AD是ΔABC的角平分线(如图),那么∠BAD= = ___;
(2)AE是ΔABC的中线(如图),那么 BE = ____=___BC。
A
D
C
B
A
B
C
E
随堂练习
2.如图在△ABC中∠ACE=∠BCE,BD=CD,则AD是三角形_____的_____线,CE是三角形_____的______线。
3.如图,在⊿ABC中,BD是角平分线,BE是中线,
(1)如果AC=10cm,则AE=____cm,
如果∠ABC=60°,则∠ABD=______
(2)如果∠A=72°, ∠C=50°,则∠ABD=______
4.如图在三角形ABC中,AD平分∠BAC,DE∥AC交AB于E点,若∠BAC=40°,则 ∠EDA=______
A
B
C
D
E
5.如图AD是△ABC的BC边上的中线,DE是△ADC的AC边上的中线,若△ABC面积等于4,则△CDE的面积等于_________ 。
1.1认识三角形(4)
如图,用铅笔可以支起一张均匀的三角形卡片,你知道怎样确定这个支撑点的位置吗?
情景导入
教学 目 标
1、了解三角形的中线、角平分线及相关性质,并能熟悉的画出这两条线段。
2、能应用三角形的中线、角平分线的性质解决简单的数学问题题。
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线(median).
三角形的“中线”定义
BE=EC
图1 16
B
C
E
A
如图1 16,
AE是BC边上的中线.
课堂探究一
(或:BC=2BE= EC)
∴BE= = BC
三角形中线的符号语言
∵AE是三角形ABC的中线。
探究三角形的“中线”性质
B
C
E
A
(1) 在纸上画出一个锐角三角形 ,并画出它的三条中线.
议一议
它们有怎样的位置关系
与同伴进行交流.
(2) 钝角三角形和直角三角形的三条中线
也有同样的位置关系吗
三角形的三条中线交于一点.
三角形的“中线”性质
三角形一边上的中线,把这个三角形分成
了两个面积相等的三角形
例、已知:AD是三角形ABC的中线,
那么:S△ABD=S△ACD 吗?为什么?
S△ACD= (三角形的面积公式)
∵AD是三角形ABC的中线 (已知)
∴BD= ( )
∴S△ABD=S△ACD
BD·AE ,
解: 过点A作AE⊥BC于点E,则
S△ABD=
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗
B
A
C
你能通过折纸的方法得到它吗
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A
的角平分线.
A
B
C
A
D
课堂探究二
D
三角形的角平分线的定义
以前所学的“角平分线”是一条射线,
B
A
C
“三角形的角平分线”
还是射线 吗
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的
线段叫三角形的角平分线.
线段
“三角形的角平分线”是一条线段.
!
D
∠1=∠2
1
2
三角形的角平分线的性质
每人准备锐角三角形、钝角三角形和直角三角形纸片各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗
(2) 你能用折纸的办法得到它们吗
(3) 在每个三角形中,这三条角平分线之间有怎样的
位置关系
将你的结果与同伴进行交流.
三角形的三条角平分线交于同一点.
1. (1)AD是ΔABC的角平分线(如图),那么∠BAD= = ___;
(2)AE是ΔABC的中线(如图),那么 BE = ____=___BC。
A
D
C
B
A
B
C
E
随堂练习
2.如图在△ABC中∠ACE=∠BCE,BD=CD,则AD是三角形_____的_____线,CE是三角形_____的______线。
3.如图,在⊿ABC中,BD是角平分线,BE是中线,
(1)如果AC=10cm,则AE=____cm,
如果∠ABC=60°,则∠ABD=______
(2)如果∠A=72°, ∠C=50°,则∠ABD=______
4.如图在三角形ABC中,AD平分∠BAC,DE∥AC交AB于E点,若∠BAC=40°,则 ∠EDA=______
A
B
C
D
E
5.如图AD是△ABC的BC边上的中线,DE是△ADC的AC边上的中线,若△ABC面积等于4,则△CDE的面积等于_________ 。
