2021-2022学年华东师大版九年级数学上册 _24.4.1.解直角三角形第一课时 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册 _24.4.1.解直角三角形第一课时 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 997.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 09:09:21 | ||
图片预览






文档简介
(共17张PPT)
第24章 解直角三角形
24.4.1 解直角三角形(第一课时)
学习目标
1.会运用勾股定理解直角三角形;(重点)
2.会运用直角三角形的两个锐角互余及锐角三角函数解直
角三角形;(重点)
3.能够把实际问题转化成解直角三角形的问题.(难点)
观察思考
B
A
C
c
b
a
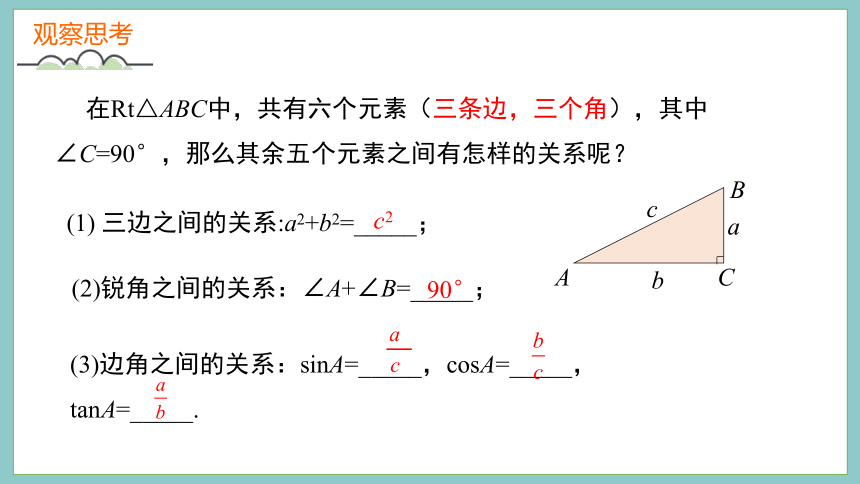
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
观察思考
问题1:什么叫解直角三角形?
在直角三角形中,由已知元素求出位置元素的过程
问题2:在直角三角形中至少要知道几个元素才能求出其他元素?
两个元素,其中至少一个元素为边
1、已知两条边的情况:勾股定理求边;三角函数求角
2、已知一个锐角和一条边的情况:互余求角;三角函数求边
知识点
已知两边解直角三角形
1
例1:在Rt△ABC中,∠C=90°,BC=3,AB=2,解直角三角形
练习:在Rt△ABC中,∠C=90°,
(1)若b=5,c= ,则∠A=_______,
∠B=______,
a=______;
(2)若a= ,b= ,则c=________,
∠A=__________,
∠B=__________.
45°
45°
5
30°
60°
知识点
已知一边一锐角解直角三角形
2
例2:在Rt△ABC中,∠C=90°,∠A=75°,AB=6,解这个直角三角形
练习:在Rt△ABC中,∠C=90°,∠B=45°,AB=63,解这个直角三角形
练习1
1. 如图,在Rt△ABC中,∠C=90°, ,解这个直角三角形.
解:
A
B
C
练习1
2. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
因为AD平分∠BAC
知识点
解直角三角形的简单应用
3
例3:如图所示,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根5米处,大树在折断之前高为多少米?
5米
5米
A
B
C
如果把题目意思改一下,求∠A 的度数该如何计算?
解:设RtΔABC中,∠B=900, AB =5m,BC=5m.
则 AC=
5+10 =15(米)
答:大树在折断之前高为15米.
知识点
解直角三角形的简单应用
3
练习:如下图,某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为多少米(结果精确到0.1,≈1.73)
解:如图所示,依题意可知,当∠B=60°时,
答:梯子的长至少3.5米
C
A
B
知识点
构造直角解直角三角形的应用
3
如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
例4:如图,在△ABC中,∠B=30°,AC=2,cos C=,则AB
边的长为____.
例5:小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成30°角,且太阳光线AD与斜坡坡面互相垂直,请你帮小明求出旗杆AB的高度(结果保留根号).
根据平行线的性质得:
解:延长AD,BC交于点M,如图所示:
答:旗杆AB的高度为
知识点
构造直角解直角三角形的应用
3
练习2
1.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
解:在Rt△CDB中,tan∠BDC=
∴BC=BD·tan40°≈4,
在Rt△BDE中,tan∠BDE=
∴BE=BDtan∠BDE=
∴CE=BE﹣BC≈4.66(m),答:广告牌EC的高度约为4.66m.
练习2
2.如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确
到0.1,参考数据:≈1.732)
解:如图,过点C作CD⊥AB于点D,
∵∠DCA=60°,∠DCB=45°,AB=380,
∴在Rt△BCD中,CD=BD,
在Rt△ACD中,tan∠DCA=
=
∴tan60°=
答:这条公路的长约为519.1米.
解题思想与方法小结:
1.数形结合思想.
方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
2.方程思想.
3.转化(化归)思想.
课堂小结
③解直角三角形,只有下面两种情况可解:
(1)已知 ;
(2)已知 。
①定义:在直角三角形中,由 求出 的过程叫做解直角三形. ;
已知元素
未知元素
②在解决实际问题时,应“ ”;
先画图,再求解
一条边和一个锐角
两条边
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
第24章 解直角三角形
24.4.1 解直角三角形(第一课时)
学习目标
1.会运用勾股定理解直角三角形;(重点)
2.会运用直角三角形的两个锐角互余及锐角三角函数解直
角三角形;(重点)
3.能够把实际问题转化成解直角三角形的问题.(难点)
观察思考
B
A
C
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
观察思考
问题1:什么叫解直角三角形?
在直角三角形中,由已知元素求出位置元素的过程
问题2:在直角三角形中至少要知道几个元素才能求出其他元素?
两个元素,其中至少一个元素为边
1、已知两条边的情况:勾股定理求边;三角函数求角
2、已知一个锐角和一条边的情况:互余求角;三角函数求边
知识点
已知两边解直角三角形
1
例1:在Rt△ABC中,∠C=90°,BC=3,AB=2,解直角三角形
练习:在Rt△ABC中,∠C=90°,
(1)若b=5,c= ,则∠A=_______,
∠B=______,
a=______;
(2)若a= ,b= ,则c=________,
∠A=__________,
∠B=__________.
45°
45°
5
30°
60°
知识点
已知一边一锐角解直角三角形
2
例2:在Rt△ABC中,∠C=90°,∠A=75°,AB=6,解这个直角三角形
练习:在Rt△ABC中,∠C=90°,∠B=45°,AB=63,解这个直角三角形
练习1
1. 如图,在Rt△ABC中,∠C=90°, ,解这个直角三角形.
解:
A
B
C
练习1
2. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
因为AD平分∠BAC
知识点
解直角三角形的简单应用
3
例3:如图所示,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根5米处,大树在折断之前高为多少米?
5米
5米
A
B
C
如果把题目意思改一下,求∠A 的度数该如何计算?
解:设RtΔABC中,∠B=900, AB =5m,BC=5m.
则 AC=
5+10 =15(米)
答:大树在折断之前高为15米.
知识点
解直角三角形的简单应用
3
练习:如下图,某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为多少米(结果精确到0.1,≈1.73)
解:如图所示,依题意可知,当∠B=60°时,
答:梯子的长至少3.5米
C
A
B
知识点
构造直角解直角三角形的应用
3
如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
例4:如图,在△ABC中,∠B=30°,AC=2,cos C=,则AB
边的长为____.
例5:小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成30°角,且太阳光线AD与斜坡坡面互相垂直,请你帮小明求出旗杆AB的高度(结果保留根号).
根据平行线的性质得:
解:延长AD,BC交于点M,如图所示:
答:旗杆AB的高度为
知识点
构造直角解直角三角形的应用
3
练习2
1.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
解:在Rt△CDB中,tan∠BDC=
∴BC=BD·tan40°≈4,
在Rt△BDE中,tan∠BDE=
∴BE=BDtan∠BDE=
∴CE=BE﹣BC≈4.66(m),答:广告牌EC的高度约为4.66m.
练习2
2.如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确
到0.1,参考数据:≈1.732)
解:如图,过点C作CD⊥AB于点D,
∵∠DCA=60°,∠DCB=45°,AB=380,
∴在Rt△BCD中,CD=BD,
在Rt△ACD中,tan∠DCA=
=
∴tan60°=
答:这条公路的长约为519.1米.
解题思想与方法小结:
1.数形结合思想.
方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
2.方程思想.
3.转化(化归)思想.
课堂小结
③解直角三角形,只有下面两种情况可解:
(1)已知 ;
(2)已知 。
①定义:在直角三角形中,由 求出 的过程叫做解直角三形. ;
已知元素
未知元素
②在解决实际问题时,应“ ”;
先画图,再求解
一条边和一个锐角
两条边
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
