云南省大理州宾川县第四高级中学2011-2012学年高二9月月考数学试题(A卷)
文档属性
| 名称 | 云南省大理州宾川县第四高级中学2011-2012学年高二9月月考数学试题(A卷) |  | |
| 格式 | zip | ||
| 文件大小 | 160.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-20 15:14:43 | ||
图片预览


文档简介
宾川县第四高级中学2011-2012学年高二9月月考
数学试题(A卷)
考生注意:1、考试时间120分钟,总分150分。
2、所有试题必须在答题卡上作答否则无效。
3、交卷时只交答题卡,请认真填写相关信息。
第I卷
选择题(每小题5分,共60分。在每小题给出的四个选项中,只有一个选项是正确的,请将答案填写在答题卡的相应位置)
1.数列1,-3,5,-7,9,…的一个通项公式为 ( )
A B C D
2.下列四个数中,哪一个是数列{}中的一项 ( )
A.380 B. 39 C. 35 D. 23
3.△ABC中,sin2A=sin2B+sin2C,则△ABC为( )
A直角三角形? B等腰直角三角形 C等边三角形 D等腰三角
4. 在△ABC中,b=,c=3,B=300,则a等于( )
A. B.12 C.或2 D.2
5.在中,根据下列条件解三角形,其中有两个解的是( )
A. b=10, A=450, C=600 B. a=6, c=5, B=600
C. a=7, b=5, A=600 D. a=14, b=16, A=450
6.在中,若,则的形状一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
7.已知数列满足, ,则此数列的通项等于( )
A. B. C. D.
8.在中,已知,,,则的面积等于 ( )
A. B. C. D.
9.在-1和8之间插入两个数a,b,使这四个数成等差数列,则 ( )
A. a=2,b=5 B. a=-2,b=5 C. a=2,b=-5 D. a=-2,b=-5
10.在△ABC中,AB=5,BC=7,AC=8,则的值为( )
A.79 B.69
C.5 D.-5
11. △ABC中,若c=,则角C的度数是( )
A.60° B.120° C.60°或120° D.45°
12.在锐角三角形中,a、b、c分别是内角A、B、C的对边,设B=2A,则的取值范围是( )
A.(-2,2) B.(0,2) C.(,2) D.(,)
二、填空题:(本大题共4小题,每小题4分,共16分)
13. 已知△ABC的周长为9,且,则cosC的值为
14.已知为等差数列,,,则____________
15.在△ABC中,若a2+b216.在△ABC中,A=60°,b=1,其面积为,则等于
三、解答题:(共6小题,共70分)解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
在△ABC中,已知,,B=45 求A、C及c
20. (本题满分12分)
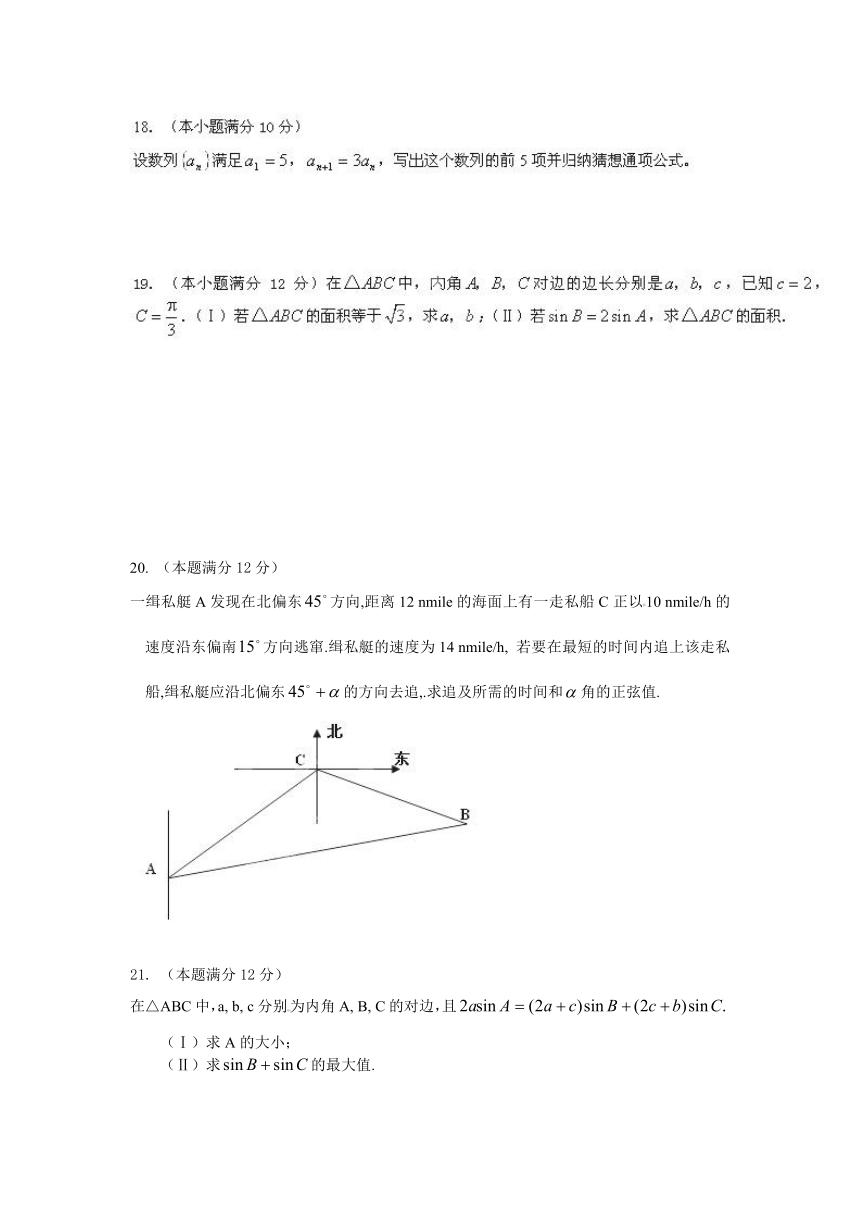
一缉私艇A发现在北偏东方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东的方向去追,.求追及所需的时间和角的正弦值.
21. (本题满分12分)
在△ABC中,a, b, c分别为内角A, B, C的对边,且
(Ⅰ)求A的大小;
(Ⅱ)求的最大值.
22. (本题满分12分)
已知、、为的三内角,且其对边分别为、、,若.
(Ⅰ)求; (Ⅱ)若,求的面积.
参考答案及评分标准
三.解答题 (6题共70分。要求写出必要的文字说明和演算步骤)
17、本题满分12分 有两解(略)
18、本题满分10分
19. 本题满分12分 解:(Ⅰ)由余弦定理得,,
又因为的面积等于,所以,得. 4分
联立方程组解得,. 6分
(Ⅱ)由正弦定理,已知条件化为, 8分
联立方程组解得,.
所以的面积. 12分
20. 本题满分12分 解: 设A,C分别表示缉私艇,走私船的位置,设经过 小时后在B处追上, 则有
,
所以所需时间2小时,
21. 本题满分12分 解:(Ⅰ)由已知,根据正弦定理得
即 由余弦定理得
故 ,A=120°
(Ⅱ)由(Ⅰ)得:
故当B=30°时,sinB+sinC取得最大值1。
22. 本题满分12分 解(Ⅰ)
又,
, .
第1页 共4页 第2页 共4页
共
数学试题(A卷)
考生注意:1、考试时间120分钟,总分150分。
2、所有试题必须在答题卡上作答否则无效。
3、交卷时只交答题卡,请认真填写相关信息。
第I卷
选择题(每小题5分,共60分。在每小题给出的四个选项中,只有一个选项是正确的,请将答案填写在答题卡的相应位置)
1.数列1,-3,5,-7,9,…的一个通项公式为 ( )
A B C D
2.下列四个数中,哪一个是数列{}中的一项 ( )
A.380 B. 39 C. 35 D. 23
3.△ABC中,sin2A=sin2B+sin2C,则△ABC为( )
A直角三角形? B等腰直角三角形 C等边三角形 D等腰三角
4. 在△ABC中,b=,c=3,B=300,则a等于( )
A. B.12 C.或2 D.2
5.在中,根据下列条件解三角形,其中有两个解的是( )
A. b=10, A=450, C=600 B. a=6, c=5, B=600
C. a=7, b=5, A=600 D. a=14, b=16, A=450
6.在中,若,则的形状一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
7.已知数列满足, ,则此数列的通项等于( )
A. B. C. D.
8.在中,已知,,,则的面积等于 ( )
A. B. C. D.
9.在-1和8之间插入两个数a,b,使这四个数成等差数列,则 ( )
A. a=2,b=5 B. a=-2,b=5 C. a=2,b=-5 D. a=-2,b=-5
10.在△ABC中,AB=5,BC=7,AC=8,则的值为( )
A.79 B.69
C.5 D.-5
11. △ABC中,若c=,则角C的度数是( )
A.60° B.120° C.60°或120° D.45°
12.在锐角三角形中,a、b、c分别是内角A、B、C的对边,设B=2A,则的取值范围是( )
A.(-2,2) B.(0,2) C.(,2) D.(,)
二、填空题:(本大题共4小题,每小题4分,共16分)
13. 已知△ABC的周长为9,且,则cosC的值为
14.已知为等差数列,,,则____________
15.在△ABC中,若a2+b2
三、解答题:(共6小题,共70分)解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
在△ABC中,已知,,B=45 求A、C及c
20. (本题满分12分)
一缉私艇A发现在北偏东方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东的方向去追,.求追及所需的时间和角的正弦值.
21. (本题满分12分)
在△ABC中,a, b, c分别为内角A, B, C的对边,且
(Ⅰ)求A的大小;
(Ⅱ)求的最大值.
22. (本题满分12分)
已知、、为的三内角,且其对边分别为、、,若.
(Ⅰ)求; (Ⅱ)若,求的面积.
参考答案及评分标准
三.解答题 (6题共70分。要求写出必要的文字说明和演算步骤)
17、本题满分12分 有两解(略)
18、本题满分10分
19. 本题满分12分 解:(Ⅰ)由余弦定理得,,
又因为的面积等于,所以,得. 4分
联立方程组解得,. 6分
(Ⅱ)由正弦定理,已知条件化为, 8分
联立方程组解得,.
所以的面积. 12分
20. 本题满分12分 解: 设A,C分别表示缉私艇,走私船的位置,设经过 小时后在B处追上, 则有
,
所以所需时间2小时,
21. 本题满分12分 解:(Ⅰ)由已知,根据正弦定理得
即 由余弦定理得
故 ,A=120°
(Ⅱ)由(Ⅰ)得:
故当B=30°时,sinB+sinC取得最大值1。
22. 本题满分12分 解(Ⅰ)
又,
, .
第1页 共4页 第2页 共4页
共
同课章节目录
