人教版八年级数学上册11.2.1 三角形的内角(第1课时)教学课件(38张)
文档属性
| 名称 | 人教版八年级数学上册11.2.1 三角形的内角(第1课时)教学课件(38张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 11:04:17 | ||
图片预览




文档简介
(共38张PPT)
11.2.1 三角形的内角 (第1课时)
人教版 数学 八年级 上册
我的形状最小, 那我的内角和 最小.
我的形状最 大,那我的 内角和最大.
不对,我有一 个钝角,所以 我的内角和才 是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角 形内角和的理解,请同学们作为小判官给它们评判一下吧.
导入新知
2. 会运用三角形内角和定理进行计算.
1. 会用平行线的性质与平角的定义证明三角形 内角和等于180°.
素养目标
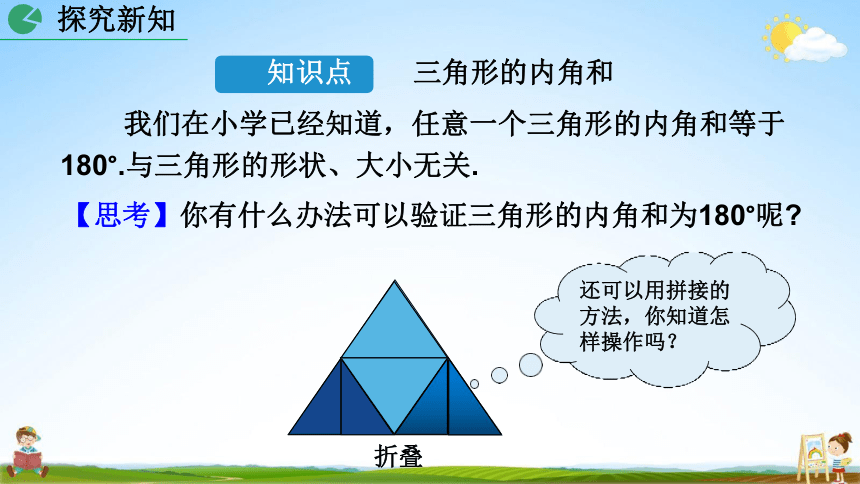
折叠
探究新知
知识点 三角形的内角和
我们在小学已经知道,任意一个三角形的内角和等于
180°.与三角形的形状、大小无关.
【思考】你有什么办法可以验证三角形的内角和为180°呢
还可以用拼接的 方法,你知道怎 样操作吗?
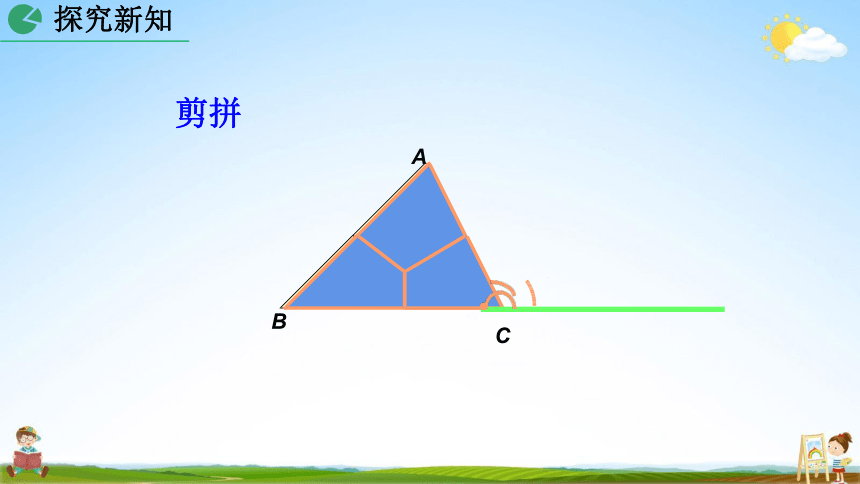
剪拼
A
B
C
2
1
探究新知
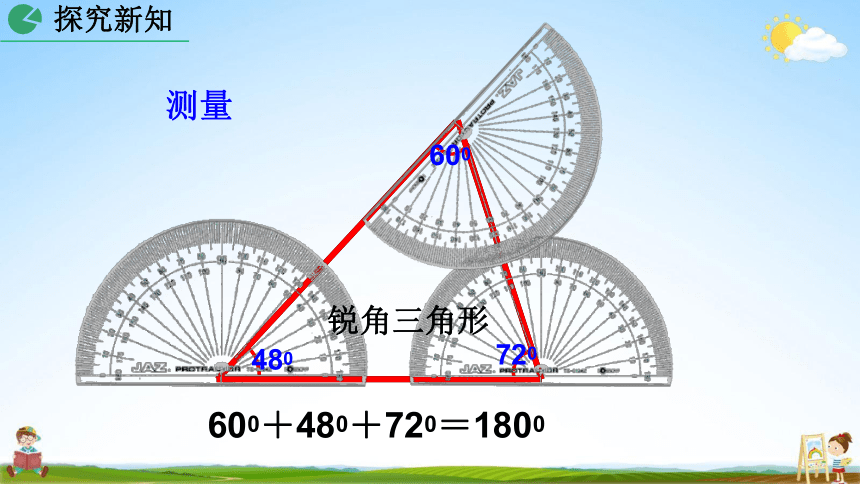
480
720
600
600+480+720=1800
探究新知
测量
锐角三角形
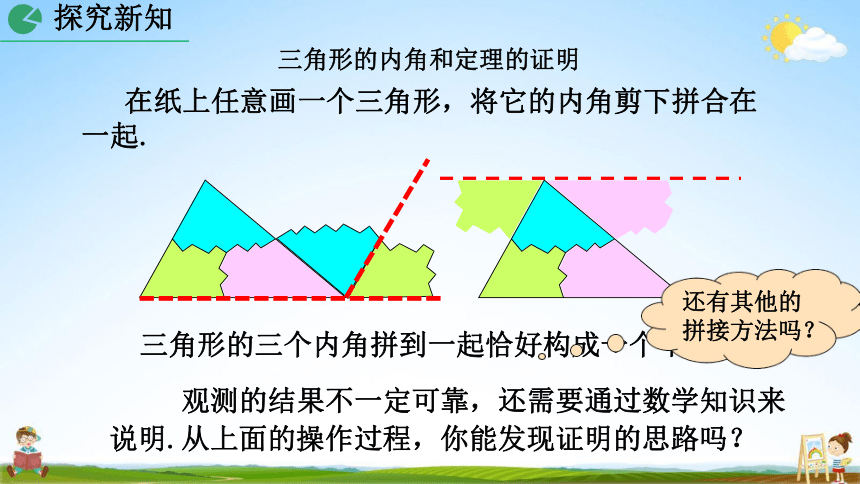
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来 说明.从上面的操作过程,你能发现证明的思路吗?
三角形的内角和定理的证明
在纸上任意画一个三角形,将它的内角剪下拼合在 一起.
探究新知
还有其他的
拼接方法吗?
l
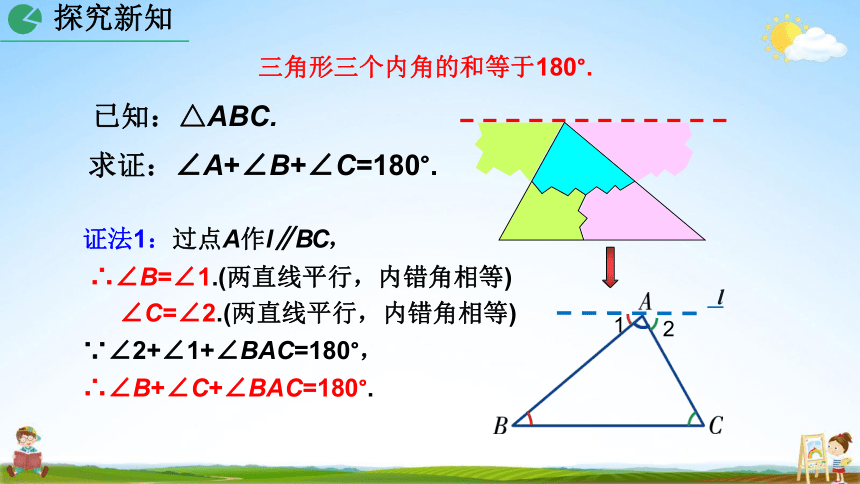
三角形三个内角的和等于180°.
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证法1:过点A作l∥BC,
∴∠B=∠1.(两直线平行,内错角相等)
∠C=∠2.(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
探究新知
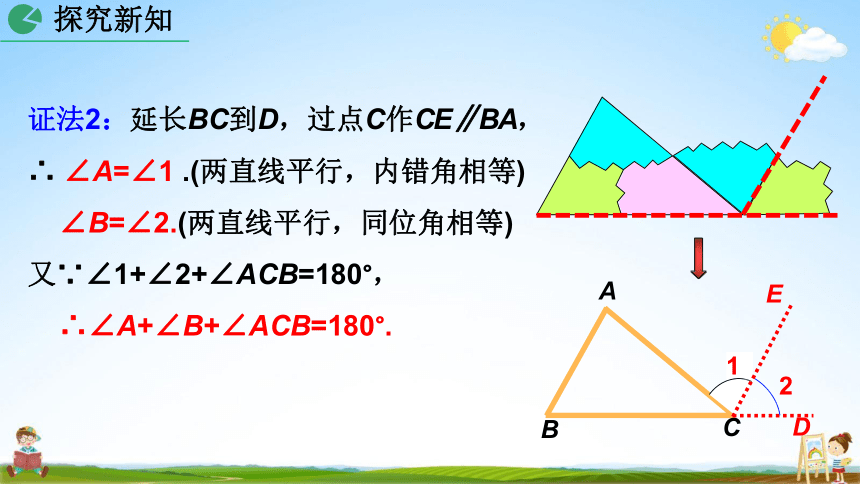
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
探究新知
C
B
A
E
D
F
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
探究新知
同学们还有其他的方法吗?
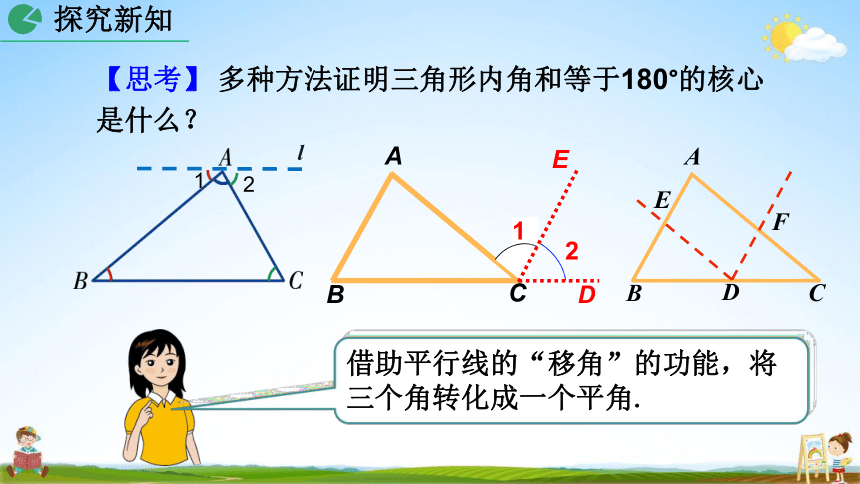
【思考】 多种方法证明三角形内角和等于180°的核心 是什么?
探究新知
l
1
2
B
E
1
2
C
A A
E
C D B D
借助平行线的“移角”的功能,将 三个角转化成一个平角.
F
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
B
G
C
2
4
A
3
E
D
F
H
1
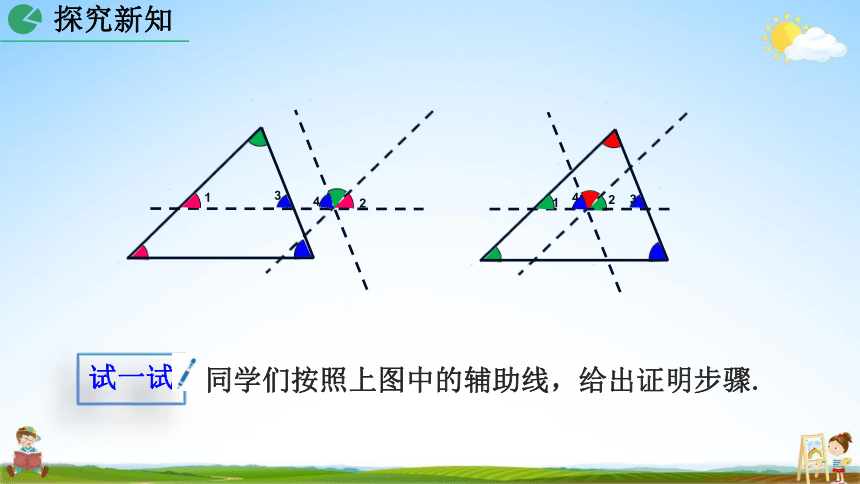
同学们按照上图中的辅助线,给出证明步骤.
探究新知
试一试
作辅助线
为了证明的需要,在原来的图形上添画的线叫做辅助 线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,通过作平行线,利用 平行线的性质,把所证问题转化为一个平角或同旁内角 互补等,这种转化思想是数学中的常用方法.
探究新知
A
B
C
D
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,
AD是△ABC的角平分线,求∠ADB的度数.
解:由∠BAC=40 °, AD是△ABC的角平分线,得
1
∠BAD=2 ∠BAC=20 °.
在△ABD中,
∠ADB=180°–∠B –∠BAD
=180°–75°–20°
=85°.
利用三角形的内角和定理求角的度数
素养考点 1
探究新知
如图,CD是∠ACB的平分线,DE∥BC,∠A=
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°–∠B –∠BCD=80°.
50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°–∠A–∠B=60°.
∵CD是∠ACB的平分线,
1
2
变 式 题
探究新知
在△ABC中,∠B=40°,∠C=80°,则∠A的度数 为(D )
A.30° B.40° C.50° D.60°
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其
中∠A = 150°,∠B= ∠D=40°.求∠C的度数.
解:∠C=180°×2–(40°+40°+150°)
=130°.
巩固练习
如图,在△ABC中,∠B=46°,∠C=54°,AD平分
∠BAC,交BC于点D,DE∥AB,交AC于点E,则
∠ADE的大小是( C )
A.45° B.54° C.40° D.50°
巩固练习
例2 如图,△ABC中,D在BC的延长线上,过D作 DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°, 求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°–∠FEA–∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°–∠CFD–∠FCD=40°.
探究新知
直线l1∥l2,一块含45°角的直角三角尺如 图放置,∠1=85°,
则∠2= .
40°
巩固练习
l1
l2
基 本
图 形
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
由三角形的内角和定理易得
∠A+∠B=∠C+∠D.
归纳总结
探究新知
3
4
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B度数为x,则∠A度数 为3x,∠C度数为(x + 15), 从 而有 3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 ,x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°,48°.
素养考点 2
方程的思想与三角形内角和定理的综合应用
探究新知
方法点拨: 三角形中 求角的度数问题,当 角之间存在数量关系 时,一般根据三角形 内角和为180°,列方 程求解.
△ABC的高,CE是∠ACB的平分线,求∠DCE的度
数.
1
1
在△ABC中,∠A=2 ∠B=3 ∠ACB,CD是
分析:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的 内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的 定义求出∠ACE即可求得∠DCE的度数.
比例关系可考虑用 方程思想求角度.
变 式 题
探究新知
2
解:∵∠A= 1 ∠B= 1 ∠ACB,
3
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°–90°–30°=60°.
∵CE是∠ACB的平分线,
1
∴∠ACE= 2 ×90°=45°,
∴∠DCE=∠ACD–∠ACE=60°–45°=15°.
探究新知
三角形 .
③在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°,
直角
则 ∠A= 60 , ∠ B=
°
50
°
,∠ C7=0 .
°
巩固练习
完成下列各题.
①在△ABC中,∠A=35°,∠ B=43 °,则∠ C=102 .
②在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是°
解析:设∠A=x,∠B=2x,∠C=3x,由三角形的内角和定理得:
x+2x+3x=180°,解得x=30°,3x=90°.
.
A
D 北
C.
东
北 E
.
B
例4 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏 东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两
岛的视角∠ABC是多少度?从C岛看A、
B两岛的视角∠ACB是多少度?
利用三角形的内角和定理解决实际问题(方位问题)
素养考点 3
探究新知
解: ∠CAB= ∠BAD– ∠CAD=80 °– 50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °.
∠ACB =180 °– ∠ABC– ∠ CAB
=180°–60°–30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的 视角∠ACB是90°.
.
A
所以∠ABE=180 °– ∠BAD=180°–80°=100°,
∠ABC= ∠ABE– ∠EBC=100°–40°=60°D. 北
在△ABC中,
C.
B
.
东
北 E
探究新知
如图,一艘渔船在B处测得灯塔A在北偏东60°的 方向,另一艘货轮在C处测得灯塔A在北偏东40° 的方向,那么在灯塔A处观看B和C处时的视角
∠BAC是多少度?
巩固练习
解:∵在B处测得灯塔A在北偏东60°的方向,
∴ ∠ABD=60°.
又∵ ∠DBE=90°,
∴ ∠ABE=90°–∠ABD=90°–60°=30°.
∵在C处测得灯塔A在北偏东40°的方向,
∴ ∠ACE=90°–40°=50°.
∴ ∠BAC=∠ACE–∠ABE=50°–30°=20°.
即在灯塔A处观看B和C处时的视角∠BAC是20°.
巩固练习
.38°
∵DE∥BC,
∴∠DCB= × 78°=39°,
∴∠CDE=∠DCB=39°.
如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作 DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE 的大小为(C )
A.44° B.40° C.39° D
解析:∵∠A=54°,∠B=48°,
∴∠ACB=180°–54°–48°=78°,
∵CD平分∠ACB交AB于点D,
连接中考
x=70
x=60
x=30
x=50
课堂检测
基 础 巩 固 题
1.求出下列各图中的x值.
B
A
C
4
D
1
3
E
2
40°
(
2. 在△ABC中,若∠A=30°,∠B=50°,则
∠C= 100°.
3. 如图,则∠1+∠2+∠3+∠4= 280 ° .
课堂检测
)
能 力 提 升 题
1. 如图,四边形ABCD中,点E在BC上,
∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的
度数. 解:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°. 又∵∠C=60°,
∴∠EDC=180°–(∠CED+∠C
=180°–(78°+60°)
=42°.
课堂检测
2.如图,在△ABC中,∠B=42°,∠C=78°,AD平 分∠BAC.求∠ADC的度数.
∴∠CAD= ∠BAC=30°,
解:∵∠B=42°,∠C=78°,
∴∠BAC=180°–∠B –∠C=60°.
∵AD平分∠BAC,
1
2
∴∠ADC=180°–∠B–∠CAD=72°.
课堂检测
数.
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
1
2
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°–60°=120°.
拓 广 探 索 题
如图,在△ABC中,BP平分∠ABC,CP平分
∠ACB,若∠BAC=60°,求∠BPC的度
课堂检测
【思考】你能直接写出∠BPC与∠A 之间的数量关系吗?
解:∵BP平分∠ABC,CP平分∠ACB,
1
∴∠PBC+∠PCB=2 (∠ABC+∠ACB).
∵∠PBC+∠PCB+∠BPC=180°,
1
∴∠BPC=180°–2(∠ABC+∠ACB)
1 1
=180°–2 (180°–∠A)=90°+ 2 ∠A .
课堂检测
求角度
证法
应用
转化为一个平角 或同旁内角互补
辅助线
三角形的内角 和等于180 °
课堂小结
课后作业
作业 内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
谢谢观看
Thank You
11.2.1 三角形的内角 (第1课时)
人教版 数学 八年级 上册
我的形状最小, 那我的内角和 最小.
我的形状最 大,那我的 内角和最大.
不对,我有一 个钝角,所以 我的内角和才 是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角 形内角和的理解,请同学们作为小判官给它们评判一下吧.
导入新知
2. 会运用三角形内角和定理进行计算.
1. 会用平行线的性质与平角的定义证明三角形 内角和等于180°.
素养目标
折叠
探究新知
知识点 三角形的内角和
我们在小学已经知道,任意一个三角形的内角和等于
180°.与三角形的形状、大小无关.
【思考】你有什么办法可以验证三角形的内角和为180°呢
还可以用拼接的 方法,你知道怎 样操作吗?
剪拼
A
B
C
2
1
探究新知
480
720
600
600+480+720=1800
探究新知
测量
锐角三角形
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来 说明.从上面的操作过程,你能发现证明的思路吗?
三角形的内角和定理的证明
在纸上任意画一个三角形,将它的内角剪下拼合在 一起.
探究新知
还有其他的
拼接方法吗?
l
三角形三个内角的和等于180°.
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证法1:过点A作l∥BC,
∴∠B=∠1.(两直线平行,内错角相等)
∠C=∠2.(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
探究新知
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
探究新知
C
B
A
E
D
F
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
探究新知
同学们还有其他的方法吗?
【思考】 多种方法证明三角形内角和等于180°的核心 是什么?
探究新知
l
1
2
B
E
1
2
C
A A
E
C D B D
借助平行线的“移角”的功能,将 三个角转化成一个平角.
F
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
B
G
C
2
4
A
3
E
D
F
H
1
同学们按照上图中的辅助线,给出证明步骤.
探究新知
试一试
作辅助线
为了证明的需要,在原来的图形上添画的线叫做辅助 线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,通过作平行线,利用 平行线的性质,把所证问题转化为一个平角或同旁内角 互补等,这种转化思想是数学中的常用方法.
探究新知
A
B
C
D
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,
AD是△ABC的角平分线,求∠ADB的度数.
解:由∠BAC=40 °, AD是△ABC的角平分线,得
1
∠BAD=2 ∠BAC=20 °.
在△ABD中,
∠ADB=180°–∠B –∠BAD
=180°–75°–20°
=85°.
利用三角形的内角和定理求角的度数
素养考点 1
探究新知
如图,CD是∠ACB的平分线,DE∥BC,∠A=
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°–∠B –∠BCD=80°.
50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°–∠A–∠B=60°.
∵CD是∠ACB的平分线,
1
2
变 式 题
探究新知
在△ABC中,∠B=40°,∠C=80°,则∠A的度数 为(D )
A.30° B.40° C.50° D.60°
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其
中∠A = 150°,∠B= ∠D=40°.求∠C的度数.
解:∠C=180°×2–(40°+40°+150°)
=130°.
巩固练习
如图,在△ABC中,∠B=46°,∠C=54°,AD平分
∠BAC,交BC于点D,DE∥AB,交AC于点E,则
∠ADE的大小是( C )
A.45° B.54° C.40° D.50°
巩固练习
例2 如图,△ABC中,D在BC的延长线上,过D作 DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°, 求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°–∠FEA–∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°–∠CFD–∠FCD=40°.
探究新知
直线l1∥l2,一块含45°角的直角三角尺如 图放置,∠1=85°,
则∠2= .
40°
巩固练习
l1
l2
基 本
图 形
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
由三角形的内角和定理易得
∠A+∠B=∠C+∠D.
归纳总结
探究新知
3
4
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B度数为x,则∠A度数 为3x,∠C度数为(x + 15), 从 而有 3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 ,x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°,48°.
素养考点 2
方程的思想与三角形内角和定理的综合应用
探究新知
方法点拨: 三角形中 求角的度数问题,当 角之间存在数量关系 时,一般根据三角形 内角和为180°,列方 程求解.
△ABC的高,CE是∠ACB的平分线,求∠DCE的度
数.
1
1
在△ABC中,∠A=2 ∠B=3 ∠ACB,CD是
分析:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的 内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的 定义求出∠ACE即可求得∠DCE的度数.
比例关系可考虑用 方程思想求角度.
变 式 题
探究新知
2
解:∵∠A= 1 ∠B= 1 ∠ACB,
3
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°–90°–30°=60°.
∵CE是∠ACB的平分线,
1
∴∠ACE= 2 ×90°=45°,
∴∠DCE=∠ACD–∠ACE=60°–45°=15°.
探究新知
三角形 .
③在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°,
直角
则 ∠A= 60 , ∠ B=
°
50
°
,∠ C7=0 .
°
巩固练习
完成下列各题.
①在△ABC中,∠A=35°,∠ B=43 °,则∠ C=102 .
②在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是°
解析:设∠A=x,∠B=2x,∠C=3x,由三角形的内角和定理得:
x+2x+3x=180°,解得x=30°,3x=90°.
.
A
D 北
C.
东
北 E
.
B
例4 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏 东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两
岛的视角∠ABC是多少度?从C岛看A、
B两岛的视角∠ACB是多少度?
利用三角形的内角和定理解决实际问题(方位问题)
素养考点 3
探究新知
解: ∠CAB= ∠BAD– ∠CAD=80 °– 50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °.
∠ACB =180 °– ∠ABC– ∠ CAB
=180°–60°–30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的 视角∠ACB是90°.
.
A
所以∠ABE=180 °– ∠BAD=180°–80°=100°,
∠ABC= ∠ABE– ∠EBC=100°–40°=60°D. 北
在△ABC中,
C.
B
.
东
北 E
探究新知
如图,一艘渔船在B处测得灯塔A在北偏东60°的 方向,另一艘货轮在C处测得灯塔A在北偏东40° 的方向,那么在灯塔A处观看B和C处时的视角
∠BAC是多少度?
巩固练习
解:∵在B处测得灯塔A在北偏东60°的方向,
∴ ∠ABD=60°.
又∵ ∠DBE=90°,
∴ ∠ABE=90°–∠ABD=90°–60°=30°.
∵在C处测得灯塔A在北偏东40°的方向,
∴ ∠ACE=90°–40°=50°.
∴ ∠BAC=∠ACE–∠ABE=50°–30°=20°.
即在灯塔A处观看B和C处时的视角∠BAC是20°.
巩固练习
.38°
∵DE∥BC,
∴∠DCB= × 78°=39°,
∴∠CDE=∠DCB=39°.
如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作 DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE 的大小为(C )
A.44° B.40° C.39° D
解析:∵∠A=54°,∠B=48°,
∴∠ACB=180°–54°–48°=78°,
∵CD平分∠ACB交AB于点D,
连接中考
x=70
x=60
x=30
x=50
课堂检测
基 础 巩 固 题
1.求出下列各图中的x值.
B
A
C
4
D
1
3
E
2
40°
(
2. 在△ABC中,若∠A=30°,∠B=50°,则
∠C= 100°.
3. 如图,则∠1+∠2+∠3+∠4= 280 ° .
课堂检测
)
能 力 提 升 题
1. 如图,四边形ABCD中,点E在BC上,
∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的
度数. 解:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°. 又∵∠C=60°,
∴∠EDC=180°–(∠CED+∠C
=180°–(78°+60°)
=42°.
课堂检测
2.如图,在△ABC中,∠B=42°,∠C=78°,AD平 分∠BAC.求∠ADC的度数.
∴∠CAD= ∠BAC=30°,
解:∵∠B=42°,∠C=78°,
∴∠BAC=180°–∠B –∠C=60°.
∵AD平分∠BAC,
1
2
∴∠ADC=180°–∠B–∠CAD=72°.
课堂检测
数.
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
1
2
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°–60°=120°.
拓 广 探 索 题
如图,在△ABC中,BP平分∠ABC,CP平分
∠ACB,若∠BAC=60°,求∠BPC的度
课堂检测
【思考】你能直接写出∠BPC与∠A 之间的数量关系吗?
解:∵BP平分∠ABC,CP平分∠ACB,
1
∴∠PBC+∠PCB=2 (∠ABC+∠ACB).
∵∠PBC+∠PCB+∠BPC=180°,
1
∴∠BPC=180°–2(∠ABC+∠ACB)
1 1
=180°–2 (180°–∠A)=90°+ 2 ∠A .
课堂检测
求角度
证法
应用
转化为一个平角 或同旁内角互补
辅助线
三角形的内角 和等于180 °
课堂小结
课后作业
作业 内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
谢谢观看
Thank You
